运筹学排班问题大作业
运筹学作业题目

运筹学作业题目1. 题目描述某物流公司需要将货物从A地运送到B地,货物数量为N件。
已知A地和B 地之间有M个中转站,每个中转站都有一定的处理能力和储存能力。
现在需要你运用运筹学的方法,给出一个最优的货物运输方案。
2. 问题分析首先,我们需要确定以下几个问题:•货物从A地到B地的最短路径是什么?•每个中转站的处理能力和储存能力分别是多少?•每个中转站的位置以及与其他中转站的距离是多少?3. 数据收集为了解决这个问题,我们需要收集以下数据:•A地和B地之间的距离•每个中转站的处理能力和储存能力•每个中转站的位置以及与其他中转站的距离4. 模型建立我们可以将这个问题建模为一个网络图问题,其中A地和B地为源点和汇点,中转站为中间节点。
我们需要找到从源点到汇点的最短路径,并且满足各个中转站的处理能力和储存能力的限制。
我们可以使用最短路径算法(如Dijkstra算法或Floyd-Warshall算法)找到从源点到汇点的最短路径,并计算出该路径上各个中转站的处理能力和储存能力。
5. 求解与优化在求解过程中,我们需要考虑以下几个方面:•最短路径的选择:我们可以根据距离、处理能力和储存能力三个因素进行综合考虑,选择最优的路径。
•货物分配策略:根据中转站的处理能力和储存能力,我们需要制定合理的货物分配策略,使得所有中转站的资源利用率最大化。
•容量约束的处理:如果某个中转站的处理能力或储存能力不足,我们需要考虑如何调整货物的分配,以避免资源浪费或堆积。
6. 结果分析根据我们的模型和求解过程,我们可以得到一个最优的货物运输方案,并且可以得到以下几个结果:•最短路径:确定了从A地到B地的最短路径,方便后续货物的运输安排。
•中转站资源利用率:根据我们的货物分配策略,可以评估每个中转站资源的利用率,进一步优化中转站的运营效果。
•资源调配建议:如果存在处理能力或储存能力不足的中转站,我们可以提供资源调配建议,帮助公司优化资源分配。
运筹学答案_第_12_章__排序与统筹方法

习题 1 解:各零件的平均停留时间为: 6p1+5p2 +4p3 +3p4 +2p5 + p1 6 由此公式可知,要让停留的平均时间最短,应该让加工时间越少的零件 排在越前面,加工时间越多的零件排在后面。 所以,此题的加工顺序为:3,7,6,4,1,2,5
习题 2 解:此题为两台机器,n 个零件模型,这种模型加工思路为:钻床上加工时v 1aFra bibliotekv 2
b
v4
c
d
v 3
设第 V 发生的时间为 x ,(V, V)间的工序提前完工的时间为 y
i
ij
目标函数 min f = 4.5(x4 −x1)+ 4y12 + y24 +4y23 + 2y34
s.t. x2 − x1 ≥3− y12 x3 − x2 ≥ 4− y23 x4 − x2 ≥7− y24 x4 − x3 ≥5− y34 x1 = 0 y12 ≤2 y23 ≤2 y24 ≤4 y34 ≤3 xi ≥ 0, yij ≥0
这个正态分布的均值 E(T) =12.08
2
2
2
其方差为:σ =σb +σd +σg =0.70 则σ =0.84
当以98%的概率来保证工作如期完成时,即:φ(u) =0.98,所以 u=2.05
此时提前开始工作的时间T满足: T −12.08 =2.05 0.84
所以T=13.8 ≈14
习题 7 解:最短的施工工时仍为4+5+6=15 具体的施工措施如下:
以上 i=1,2,3,4; j=1,2,3,4 用管理运筹学软件中的线性规划部分求解,得到如下结果: minf=46.5 x1=0,x2=1, x3=5,x4=7,
运筹学作业(一)

《运筹学》作业(一)题1.某货轮分前、中、后三个舱位,结构参数见表1。
拟装运三种货物,性能参数见表2。
为了航运安全,要求舱位之间载重比例的偏差不超过10%,以保持船体的平衡。
问应如何制订货物的装运方案可使此运输的收益达到最大?建立该问题的LP 模型。
提示:用x ij 表示装运在第i 个舱位中的第j 种货物的重量,其中:i = 前, 中, 后; j = A, B, C ;故一共有9个变量。
目标是使总运费达到最大。
约束条件分为四组:每个舱位中货物的体积限制,重量限制,每种货物的数量限制,和舱位之间载重比例的偏差限制,故一共有12个约束条件。
题2.确定下列约束条件构成的可行域(1) ⎪⎩⎪⎨⎧≥≤+无约束 2121042x x x x (2)⎪⎩⎪⎨⎧≥-无约束无约束 21210x x x x (3) ⎪⎩⎪⎨⎧≥=≤+-05222121 x x x x (4) ⎪⎩⎪⎨⎧=≥≤+21422121 x x x x 题3.已知LP 问题: 0,,,844344243214213214321≥=++=++-++=x x x x x x x x x x x x x x Z s.t.max试确定⎪⎪⎭⎫ ⎝⎛-==-4/114/10,),(132B x x x B T 是否为最优解。
如果是,给出最优目标值;否则,确定新一轮的进、出变量。
提示 检验数 j j B j c p B c -=-1λ,j = 1, 4。
如果检验数的值大于或等于零,则为最优解;否则,令绝对值最大的负检验数对应的非基本变量进入,而令最小正比值对应的基本变量退出。
题4.给定LP 问题: 0,,42044602343025233212131321321≥≤+≤+≤++++=x x x x x x x x x x x x x Z s.t .m a x已知其最优解为:⎪⎪⎪⎭⎫ ⎝⎛--===-11202/1004/12/1,)20,230,100(),,(1632B x x x x T B T。
(完整word版)《运筹学》_第六章排队论习题及_答案

《运筹学》第六章排队论习题转载请注明1. 思考题(1)排队论主要研究的问题是什么;(2)试述排队模型的种类及各部分的特征;(3)Kendall 符号C B A Z Y X /////中各字母的分别代表什么意义;(4)理解平均到达率、平均服务率、平均服务时间和顾客到达间隔时间等概念; (5)分别写出普阿松分布、负指数分布、爱尔朗分布的密度函数,说明这些分布的主要性质;(6)试述队长和排队长;等待时间和逗留时间;忙期和闲期等概念及他们之间的联系与区别。
2.判断下列说法是否正确(1)若到达排队系统的顾客为普阿松流,则依次到达的两名顾客之间的间隔时间服从负指数分布;(2)假如到达排队系统的顾客来自两个方面,分别服从普阿松分布,则这两部分顾客合起来的顾客流仍为普阿松分布;(3)若两两顾客依次到达的间隔时间服从负指数分布,又将顾客按到达先后排序,则第1、3、5、7,┉名顾客到达的间隔时间也服从负指数分布; (4)对1//M M 或C M M //的排队系统,服务完毕离开系统的顾客流也为普阿松流; (5)在排队系统中,一般假定对顾客服务时间的分布为负指数分布,这是因为通过对大量实际系统的统计研究,这样的假定比较合理;(6)一个排队系统中,不管顾客到达和服务时间的情况如何,只要运行足够长的时间后,系统将进入稳定状态;(7)排队系统中,顾客等待时间的分布不受排队服务规则的影响;(8)在顾客到达及机构服务时间的分布相同的情况下,对容量有限的排队系统,顾客的平均等待时间少于允许队长无限的系统;(9)在顾客到达分布相同的情况下,顾客的平均等待时间同服务时间分布的方差大小有关,当服务时间分布的方差越大时,顾客的平均等待时间就越长; (10)在机器发生故障的概率及工人修复一台机器的时间分布不变的条件下,由1名工人看管5台机器,或由3名工人联合看管15台机器时,机器因故障等待工人维修的平均时间不变。
3.某店有一个修理工人,顾客到达过程为Poisson 流,平均每小时3人,修理时间服从负指数分布,平均需19分钟,求: (1)店内空闲的时间; (2)有4个顾客的概率; (3)至少有一个顾客的概率; (4)店内顾客的平均数; (5)等待服务的顾客数; (6)平均等待修理的时间;(7)一个顾客在店内逗留时间超过15分钟的概率。
运筹学上机作业答案
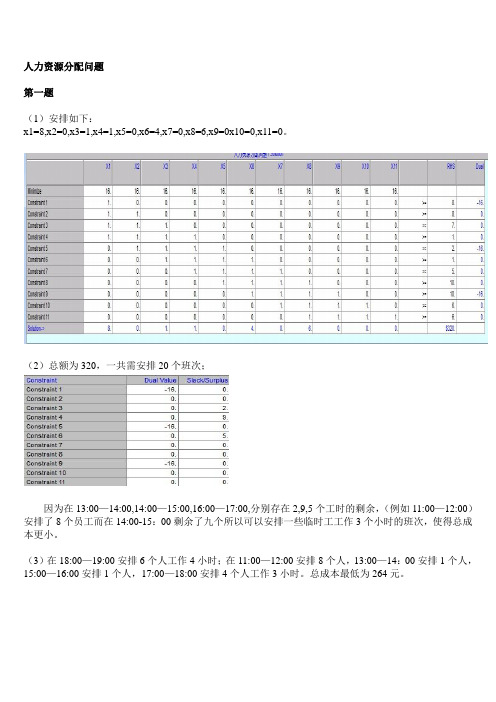
人力资源分配问题第一题(1)安排如下:x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0x10=0,x11=0。
(2)总额为320,一共需安排20个班次;因为在13:00—14:00,14:00—15:00,16:00—17:00,分别存在2,9,5个工时的剩余,(例如11:00—12:00)安排了8个员工而在14:00-15:00剩余了九个所以可以安排一些临时工工作3个小时的班次,使得总成本更小。
(3)在18:00—19:00安排6个人工作4小时;在11:00—12:00安排8个人,13:00—14:00安排1个人,15:00—16:00安排1个人,17:00—18:00安排4个人工作3小时。
总成本最低为264元。
生产计划优化问题第二题产品1在A1生产数量为1200单位,在A2上生产数量为230单位,在B1上不生产,B2上生产数量为858单位,B3上生产数量为571单位;产品2在A1上不生产,在A2上生产数量为500单位,在B1上生产数量为500单位;产品3在A2上生产数量为324单位,在B2上生产数量为324单位。
最大利润为2293.29元。
第三题设Xi为产品i最佳生产量。
(1)最优生产方案唯一,为X1=1000、X2=1000、X3=1000、X4=1000、X5=1000、X6=55625、X7=1000. (2)如上图所示,产品5的单价价格为0-30时,现行生产方案保持最优。
(3)由于环织机工的影子价格为300,且剩余变量值为零,而其他几种资源的影子价格为0,剩余变量均大于0,所以应优先增加环织工时这种资源的限额,能增加3.33工时,单位费用应低于其影子价格300才是合算的。
(4)因为产品2对偶价格= -3.2<0 ,950>933.33,3.2*(1000-950)=160;所以当产品2的最低销量从1000减少到950时,总利润增加160元。
运筹学作业

运筹学作业-2(共5页) -本页仅作为预览文档封面,使用时请删除本页-一、 实验内容及步骤(包含简要的实验步骤流程) 问题:大学生值班问题东方大学计算机实验室聘用4名大学生(代号1、2、3、4)和2名研究生(代号5、6)值班答疑。
已知每人从周一至周五每天最多可安排的值班时间及每人每h 值班报酬如下表所示:表学生代号 报酬 (元/h ) 每人最多可安排的值班时间周一 周二 周三 周四 周五1 6 0 6 0 72 0 6 0 6 034 8 3 05 4 5 56 0 4 5 3 0 4 8 0 6 0 6 0 6 3该实验室开放时间为上午8:00至晚上10:00,开放时间内须有且仅须有一名学生值班。
规定大学生每周值班不少于8h ,研究生每周值班不少于7h ,每名学生每周值班不超过3次,每次值班不少于2h ,每天安排值班的学生不超过3人,且其中必须有一名研究生。
施为该实验室安排一张人员值班表,使总支付的报酬为最少。
模型建立:解:设为学生i 在周j 的值班时间,10ij y ⎧⎪⎨⎪⎩=,安排学生i 在周j 值班,否则用代表学生i 在周j 最对可安排的值班时间,为学生i 的每h 的报酬,则本题的数学模型为:6511min iiji j z c x===∑∑@for(weeks(J):yi(5,J)+yi(6,J)>=1);!非零约束;@for(weeks(J):@for(students(I):times(I,J)>=0)); !0-1变量;@for(sw:@bin(yi));data:c=10 10 10 10 1010 10 10 10 10;ai=6 0 6 0 70 6 0 6 04 8 3 0 55 56 0 43 04 8 00 6 0 6 3;enddataend运行结果:根据结果我们可以得到下面这张安排表:表2:最终安排表学生代号报酬(元/h)每人最多可安排的值班时间周一周二周三周四周五1 6 6 72 4 638 54 5 65 3 2 560 2 3 2 根据这张安排表安排,最终需要支付的最低报酬 min=。
运筹学作业(5)
运筹学作业(5)
习题1、清华大学运筹学(第三版)P112 4.2(2)
用图解法找出以下目标规划问题的满意解。
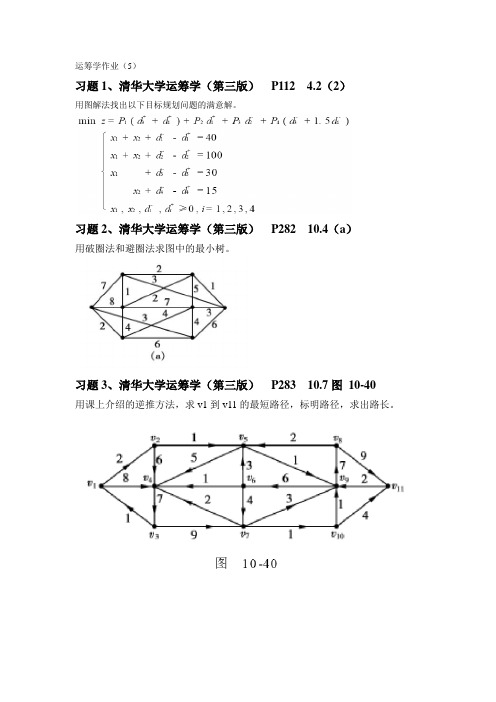
习题2、清华大学运筹学(第三版)P282 10.4(a)
用破圈法和避圈法求图中的最小树。
习题3、清华大学运筹学(第三版)P283 10.7图10-40
用课上介绍的逆推方法,求v1到v11的最短路径,标明路径,求出路长。
习题4:已知条件如表所示
p1:每周总利润不得低于10000元;
p2:因合同要求,A型机每周至少生产10台,B型机每周至少生产15台;
p3:希望工序Ⅰ的每周生产时间正好为150小时,工序Ⅱ的生产时间最好用足,甚至可适当加班。
试建立这个问题的目标规划模型并求解(可利用EXCEL求)。
思考题:在上题中,如果工序Ⅱ在加班时间内生产出来的产品,每台A型机减
少利润10元,每台B型机减少利润25元,并且工序Ⅱ的加班时间每周最多不超过30小时,这是p4级目标,试建立这个问题的目标规划模型并求解。
(此题下周四前会给出参考答案)。
运筹学 大作业

运筹学请在以下五组题目中任选一组作答,满分100分。
第一组:计算题(每小题25分,共100分)1.福安商场是个中型的百货商场,它对售货人员的需求经过统计分析如下表所示,为了保证售货人员充分休息,售货人员每周工作五天,休息两天,并要求休息的两天是连续的,问该如何安排售货人员的休息,既满足了工作需要,又使配备的售货人员的人数最少,请列出此问题的数学模型。
2.A、B两人分别有10分(1角)、5分、1分的硬币各一枚,双方都不知道的情况下各出一枚,规定和为偶数,A赢得8所出硬币,和为奇数,8赢得A所出硬币,试据此列出二人零和对策模型,并说明此游戏对双方是否公平。
3、某厂生产甲、乙两种产品,这两种产品均需在A、B、C三种不同的设备上加工,每种产品在不同设备上加工所需的工时不同,这些产品销售后所能获得利润以及这三种加工设备问:该厂应如何组织生产,即生产多少甲、乙产品使得该厂的总利润为最大?4、用图解法求解 max z = 6x1+4x2 s.t.第二组:计算题(每小题25分,共100分)1、用图解法求解min z =-3x1+x2 s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤+≥+≤≤08212523421212121x x x x x x x x ,2、用单纯形法求解 max z =70x1+30x2 s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+072039450555409321212121x x x x x x x x ,3、用单纯形法求解 max z =7x1+12x2 s.t.⑵ ⑶ ⑷ ⑸、⑹1212212210870x x x x x x x +≤⎧⎪+≤⎪⎨≤⎪⎪≥⎩, ⑴ ⑵ ⑶ ⑷ ⑸⑹、⑺⑴⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200543604921212121x x x x x x x x ,4.某企业要用三种原材料A 、B 、C 生产出出三种不同规格的产品甲、乙、丙。
已知产品的规格要求,产品单价,每天能供应的原材料数量及原材料单价,分别见表1和表2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学排班问题的建模和程序设计报告2011级工业工程一班杨添淇1120110892********************** 0.前言本报告共分为五个部分:1.排班问题的提出2.建模的心路历程3.新的背景与设定4.新的建模5.建模后的思考其中,第二部分与第五部分最为用力,集中体现了作者想要表达的观点。
其实这两部分应该写在分析报告里吧?好像搞反了…是为序。
1.排班问题的提出某小区组建维修保洁服务,现需要招聘维修保洁人员若干轮班工作。
其中包括电工,水管工,和保洁员。
工作采用计时制,每人工作满8小时后可以下班,如张三在6点上班,可在下午2点下班。
根据统计,小区需求人数如下表:时间电工水管工保洁0点-2点 1 0 02点-4点0 0 04点-6点0 0 06点-8点 6 3 08点-10点8 6 310点-12点9 5 712点-14点 4 4 314点-16点8 7 516点-18点 4 12 1018点-20点12 16 620点-22点 5 8 222点-24点 3 2 0维修保洁服务的收费标准是:电工25元/小时,水工20元/小时,保洁15元/小时。
试制定招聘计划和工人的排班表(即:招聘工人的数量和每个工人的上班时间)。
2.建模的心路历程余以为,老师要我们交报告,绝不是走个形式,也不仅仅是要看我们写出的冷冰冰的代码,求解问题的能力,更是要看我们思维的走向:从哪里来,到哪里去,最终形成一条清晰的路径。
确实,看这个路径的形成过程是一件非常有趣的事,记录这个过程亦然。
是故,我采用了完全写实的笔法,彻头彻尾地记录下了自己的真实想法,怎么想的怎么写的,想怎么写就怎么写。
所以,报告的这个部分叫做:建模的心路历程(多么温润而厚重的小标题啊)。
问题的最后提到了收费问题,旋即戛然而止,留给了解题人无限的遐想空间。
我想老师的本意,是好的。
但读完题后,我的第一个问题便出在这最后一句上:“收费标准”中的“收费”二字作何解。
从语法角度上来讲,这是一个没有主语的动词做了“标准”二字的定语。
“收费”这个动作的主语对我们求解这个问题,起着至关重要的作用。
从一个久经考场的学生的角度来看,这个收费标准应该等同于工资来看:因为工资标准在这道问题中是除了用工需求外最应该出现的已知条件,而且与聘用资费优化息息相关。
而从一个居民,一个一般人的角度来看,收费应该指的是工作的时候向住户收取的费用。
其唯如此,才可以真正称得上是收费。
但是转念一想,我交了一年的物业费,中间再有什么问题的话你来维修是不该收取任何费用的。
这就像买了保险之后得了病,不能说自己再把医药费全扛下来,那样保险就没用了。
再退一步说,就算交了物业费再找电工维修需要再交钱的话,也不应该按照时长收费——保洁倒还罢了,水管工要是为了多赚点收入一个阀门拧了一上午,那就太不美好了。
所以,我更倾向于第一种观点。
毕竟我也是一个久经考场的学生。
是故,以下所有建模过程都基于这个假定:即25元每小时是我们付给电工的工钱,水管工保洁工依此类推。
有人就会说了,这个收费到底是怎么回事,问老师一下不就清楚了。
这就是我一直想说的另一个问题:为什么学生不愿意和老师交流。
但这与建模毫无关系,所以我会在我其他的杂文里探讨这个问题,于此不做过多阐述,还是说建模的事。
排除了这个歧义项的干扰,这个问题还是有很大的解释空间的。
诚然,小小的收费二字没有影响问题本身,这依然是一个开放式的问题,允许我们设定各种各样的环境,来解出各种不同的答案。
那么首先最容易想到的情况,一定是三个工种各自招人,每个时段的工作人数都必须大于等于统计需求人数,也就是什么都不加。
于是不难得出数学模型如下,以电工为例:依据表格将全天24小时划分成十二个时段,每两小时一段。
设每个偶数整点时刻开始工作的人数分别为X1,X2,X3…X12,目标值F= X1+X2+X3+…+X12,求其最小值。
则有线性方程组:F= X1+X2+X3+…+X12X1+X10+X11+X12>1X1+X2+X11+X12>0X1+X2+X3+X12>0X1+X2+X3+X4>6...X9+X10+X11+X12>0这是一个典型的线性规划问题(话说这方程组好大…)。
幸好现代的计算机技术可以帮助我们方便快捷地求解此类问题,不然手动求解这个方程组的情形真的是不敢想象。
似乎问题到这里已经被解决的差不多了。
可是有一个严重的问题是:我根本不会用matlab……后来,在花掉了n个积攒多年的百度文库财富值之后,终于学会了matlab中基本线性规划问题的求解方法:即应用matlab中的linprog函数。
由于linprog函数只能求解约束条件为balabala小于等于某定值的方程,所以将各个约束条件进行了变形处理,最终得到以下的指令:Matlab中的指令如下:F=[1;1;1;1;1;1;1;1;1;1;1;1];a=[-1 0 0 0 0 0 0 0 0 -1 -1 -1;-1 -1 0 0 0 0 0 0 0 0 -1 -1;-1 -1 -1 0 0 0 0 0 0 0 0 -1;-1 -1 -1 -1 0 0 0 0 0 0 0 0;0 -1 -1 -1 -1 0 0 0 0 0 0 0;0 0 -1 -1 -1 -1 0 0 0 0 0 0;0 0 0 -1 -1 -1 -1 0 0 0 0 0;0 0 0 0 -1 -1 -1 -1 0 0 0 0;0 0 0 0 0 -1 -1 -1 -1 0 0 0;0 0 0 0 0 0 -1 -1 -1 -1 0 0;0 0 0 0 0 0 0 -1 -1 -1 -1 0;0 0 0 0 0 0 0 0 -1 -1 -1 -1];b=[-1;0;0;-6;-8;-9;-4;-8;-4;-12;-5;-3];vbl=[0;0;0;0;0;0;0;0;0;0;0;0];[x,fval]=linprog(F,a,b,[],[],vbl)运行结果如下:Optimization terminated.x =0.00000.00003.49733.26401.70950.52922.97134.23751.52503.26620.00000.0000fval =21.0000可是作为一个实际问题,尤其是这种涉及到人数的实际问题的时候,是不允许非整数解的存在的,毕竟我们不能叫半个人去工作,这样太不人道,也不好实现。
况且0.6个人加上0.4个人也再不能等于一个完整的人了,这个拆分过程是不可逆的。
所以我对于机器解出的数据进行了一个最基本的整理,即四舍五入:X= 当前工作人数所需工作人数剩余工时0 3 1 20 0 0 03 3 0 33 6 6 02 8 8 01 9 9 03 94 54 10 8 22 10 4 63 12 12 00 9 5 40 5 3 2fval=21以上解决方案满足需求条件。
水管工与保洁工运算过程类似。
建模过程不再粘贴,凑字数什么的最讨厌了。
可是我们不难发现,机器明显不够智能的地方。
具体体现在四点到六点上:明明没有人需要电工却叫人家大早上四点来上班,呆上两个小时再工作。
如果是我的话,我一定会把老板骂个满头大包,就算你给我工钱也不能这么欺负人。
更严重的问题在于工时的浪费。
为了满足十点到十二点,十八点到二十点两个略显变态的时段,造成了大量的工时浪费:工人在这两个时间段干完工作之后,剩下的时间会闲下来喝茶看报纸。
这样无形中造成了人员的冗余。
浪费是可耻的。
尤其是在现在这种用工荒的大环境下,对于劳动力的闲置何止是可耻,简直应该说是犯罪。
而我们又不得不满足这些上帝客户们的需求。
因此,为了支持建设节约集约型社会,我们必须要改变问题的背景设定和先决条件。
3.新的背景与设定1.作为一个贪心的老板的话,我一定会考虑招聘既能当电工又能当水管工还能兼职保洁的工人。
这样的话请一个人再怎么说也一定比请三个人便宜,毕竟他只吃一份盒饭,只要养活一个家庭。
但是,暂且不论有没有这样一专多能的人才技工,工作时间的冲突和连续工作带来的疲劳也成了这种兼职的巨大障碍。
所以,虽然很贪心,我还是放弃了这种又想马儿跑,又想马儿少吃草的天真想法。
2.如果是作为一个为了降低成本可以无所不用其极的提供服务的一方的话,首先想到的是:急什么急,有问题人手不够就让他们等一会,得了呗。
对此我实在是不敢苟同。
且不论人们对于脏乱差环境的容忍程度有多强,保洁是不是一种对于服务速度要求特高的服务项目;正常住户一般最忍不了的两件事就是停电停水或者漏电漏水(物理老师说电和水性质相似,呜呼诚不我欺)。
所以,余以为,抢险维修服务一类的工种,性质和保镖类似,失误一次就可以辞职回家了。
任谁也不能容忍家里的水管如喷泉般肆虐。
是故这两种问题的解决必须要及时,即不能等待。
3.排除了上面这两种可能性之后,我们似乎已经无计可施了。
但是,如果把思路逆转过来的话,是不是就会好很多——我可以改变工人的工作方式,让一部分人跳着工作,以零代整,削减高峰时段的用人数避免浪费,再其他时段浪费出来的工时的填补高峰时段的空缺。
这样就减少了工时的浪费。
中国的廉价劳动力们没有那么大的大爷脾气,非八小时连续不干;他们要的也不多,有的只需求温饱即可。
况且题干中说的只是“工作采用计时制,每人工作满8小时后可以下班,如张三在6点上班,可在下午2点下班。
”其中“可以”二字,最其妙者——又没说一定要满八小时才能下班,不满八小时按八小时计多不退少要补。
但是如果把所有工人的工作时间都拆成零零碎碎的话,似乎有点太无赖了,那就不要规划了。
这像是钻了题目表述的空子。
那么我们不妨再逆转一下思路:每个工种选出一到数个队长/模范/红旗手/小标兵/灵活机动岗,多付三分之一的工钱,然后全天值班待命,哪里需要哪里搬。
这就是我的第二种建模方案,它真真切切地减小了用工高峰时段的需求值。
4.新的建模根据初步估量,暂拟订设立三个值班岗。
此三人的八个小时分成四部分,分摊在几个高峰值上。
将八点到十点,十点到十二点,十四点到十六点,十八点到二十点,四个时段的需求人数分别减去3,由活动岗代替。
Matlab 指令如下:f=[1;1;1;1;1;1;1;1;1;1;1;1];a=[-1 0 0 0 0 0 0 0 0 -1 -1 -1;-1 -1 0 0 0 0 0 0 0 0 -1 -1;-1 -1 -1 0 0 0 0 0 0 0 0 -1;-1 -1 -1 -1 0 0 0 0 0 0 0 0;0 -1 -1 -1 -1 0 0 0 0 0 0 0;0 0 -1 -1 -1 -1 0 0 0 0 0 0;0 0 0 -1 -1 -1 -1 0 0 0 0 0;0 0 0 0 -1 -1 -1 -1 0 0 0 0;0 0 0 0 0 -1 -1 -1 -1 0 0 0;0 0 0 0 0 0 -1 -1 -1 -1 0 0;0 0 0 0 0 0 0 -1 -1 -1 -1 0;0 0 0 0 0 0 0 0 -1 -1 -1 -1];b=[-1;0;0;-6;-5;-6;-4;-5;-4;-9;-5;-3];vbl=[0;0;0;0;0;0;0;0;0;0;0;0];[x,fval]=linprog(f,a,b,[],[],vbl)运行结果如下:x =0.00000.00002.56083.43920.00000.00002.68162.80841.11532.39460.00000.0000fval =15.0000经整理,实际人数如下:X= 当前工作人数所需工作人数剩余工时0 3 1 20 0 0 00 0 0 06 6 6 00+3 9 8 10+3 9 9 03 94 53+3 9 8 11 7 4 33+3 13 12 10 7 5 20 4 3 1依然满足条件,且省下了21-15-3*4/3=2,两个人的工钱。
