第25章解直角三角形检测试题
解直角三角形练习题及答案经典

28.2 解直角三角形 一、选择题 1、如图,已知正方形ABCD 的边长为2,如果将线段BD 绕着点B 旋转后,点D 落在CB 的延长线上的D ′处,那么tan ∠BAD ′等于( )(A).1(B).2 (C).22 (D).22 2、如果α是锐角,且54cos =α,那么αsin 的值是( ). (A )259 (B ) 54 (C )53 (D )2516 3、等腰三角形底边长为10㎝,周长为36cm ,那么底角的余弦等于( ). (A )513 (B )1213 (C )1013 (D )512 4、. 以下不能构成三角形三边长的数组是 ( )(A )(1,3,2) (B )(3,4,5) (C )(3,4,5) (D )(32,42,52)5、在Rt △ABC 中,∠C =90°,下列式子中正确的是( ).(A )B A sin sin = (B )B A cos sin =(C )B A tan tan = (D )B A cot cot =6、在矩形ABCD 中,DE ⊥AC 于E ,设∠ADE=α,且53cos =α, AB = 4, 则AD 的长为( ).(A )3 (B )316 (C )320 (D )516 7、某市在“旧城改造”中计划在一块如图所示的三角形空地上种植某种草皮以美 化环境,已知这种草皮每平方米a 元,则购买这种草皮至少要( ).(A )450a 元 (B )225a 元 (C )150a 元 (D )300a 元8、已知α为锐角,tan (90°-α)=3,则α的度数为( )(A )30° (B )45° (C )60° (D )75°9、在△ABC 中,∠C =90°,BC =5,AB =13,则sin A 的值是( )(A )135 (B )1312 (C )125 (D )512 10、如果∠a 是等边三角形的一个内角,那么cos a 的值等于( ). A B CDE ︒15020米30米(A )21 (B )22 (C )23 (D )1 二、填空题 11、如图,在△ABC 中,若∠A =30°,∠B =45°,AC =22, 则BC = w12、如图,沿倾斜角为30︒的山坡植树,要求相邻两棵树的水平距离AC 为2m ,那么相邻两棵树的斜坡距离AB 为 m 。
第25章 解直角三角形单元测试卷(含答案)

BAC(第3题图)(第4题图)第25章 解直角三角形单元测试卷班级:__________ 座号:__________ 姓名:__________________ 成绩:___________一、选择题(每小题4分,共24分)1.cos60°的值等于………………………………………………………………………( ) A .12 B .22 C .32 D .12.如图,在Rt △ABC 中,∠ACB=Rt ∠,BC=1,AB=2,则下列结论正确的是…( ) A .sinA=32 B .tanA= 12C .cosB=32 D .tanB= 33.如图,点P (3,4)是∠a 的边OA 上的一点,则tan a =( )A . 35B . 45C .34D .43 4.已知a 为锐角,且sin (a -10°)=32,则a 等于………………………………( ) A .50° B .60° C .70° D .80°5.已知a 为锐角,则m=sin a +cos a ,则m 的值为…………………………………( ) A .m >1 B .m =1 C .m <1 D .m ≥16.正方形网格中,△ABC 的位置如图所示,则cos ∠B 的值为………………………( ) A .12 B .22 C .32 D .33二、填空题(每题3分,共36分) 7.已知∠A 为锐角,若sinA=22,则∠A=__________度 8.计算:2sin60°=____________9.某坡面的坡度为1: 3 ,则坡角是______________度10.在△ABC 中,∠C=90° ,若tanA=12 ,则sinA=_________11.计算:sin 263°+ cos 263°=_________________CDD'B A(第18题图)B A CA C 12.在△ABC 中,∠C=90°,AC=BC=1,则tanA=______________ 13.用计算器计算:sin54°25’ ≈_______________(精确到0.0001) 14.在Rt △ABC 中,∠C=90° ,若sinA=35 ,则cosB=_________15.直角三角形的两条直角边分别为6、8,则斜边上的中线的长为______________ 16.化简:(sin85°-1)2 =____________17.某飞机在离地面1200 3 米的上空测得地面控制点的俯角为60°,此时飞机与该地面控制点之间的距离是____________米。
【九年级】九年级上册第25章解直角三角形测试题(华师大版有答案)

【九年级】九年级上册第25章解直角三角形测试题(华师大版有答案)第25章解直角三角形检测题(时间:90分钟,满分:100分)一、(每小题3分,共30分)1.计算:a.b.c.d.2.在△, ∠ = 90°,如果,,那么sin的值是()a.b.c.d.3.在△, ∠ = 90,然后是罪()a.b.c.d.4.在△ ABC,如果三边BC、Ca和ab满足BC∶ Ca∶ AB=5∶ 12∶ 13,然后CoSb() a.b.c.d.5.在△, ∠ = 90°,则sin的值为()a.b.c.1d.6.已知于,,则的值为()a.b.c.d.7.如图所示,一个小球沿着斜坡从地面向上移动10。
此时,小球离地面的高度为()a.b.2c.4d.8.如图所示,在钻石中,,,Tan的值∠ 是()a.b.2c.d.9.如果直角三角形的两条右边之和为7,面积为6,则斜边的长度为()a.5b.c.7d.10.如图所示,已知45°<a<90°,则以下公式为真()a.b.c、 d。
二、题(每小题3分,共24分)11.那么__12.若∠是锐角,cos=,则∠=_________.13.小兰想测量南塔的高度她抬头看了看塔顶,测量了30°的仰角,然后向塔的方向移动了50°,测量了60°的仰角,所以塔的高度大约是___________________14.等腰三角形的腰长为2,腰上的高为1,则它的底角等于________.15.如图所示,如果斜面上的高度为RT△ 那就知道了___16.△abc的顶点都在方格纸的格点上,则_.17.数字① 是中国古代著名的“赵双弦图”的示意图,它被四个全等的直角三角形包围。
如果四个直角三角形中边长为6的直角边向外翻倍,得到图中所示的“数学风车”②, 风车的周长是____18.如图是一个艺术窗的一部分,所有的四边形都是正方形,三角形是直角三角形,其中最大正方形的边长为,则正方形a,b的面积和是_________.三、回答问题(共46分)19.(8分)计算下列各题:(1);(2).20.(6分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:(1)在树前的平地上选择一个点,测量树顶与该点的仰角为35°;(2)在点和大树之间选择一点(、、在同一直线上),测得由点看大树顶端的仰角恰好为45°;(3)两个测量点之间的距离为4.5请你根据以上数据求出大树的高度.(结果保留3个有效数字)21.(6分)每年的5月15日是“世界残疾人日”。
人教版九年级下册数学《解直角三角形》测试题及答案

P42、35、当x=时,无意义.(00<x<900)6、求值:sin60︒⨯2sinx-cosxA.1515344A.50°B.40°C.(15040解直角三角形测试题一、填空题1、如图:是∠α的边OA上一点,且P点的坐标为(3,),则sin(900-α)=_____________.2可用锐角的余弦表示成__________.△3、在ABC中,∠ACB=900,CD⊥AB于D,若AC=4,BD=7,则sinA=,tanB=.4、若α为锐角,tanα=12,则sinα=,cosα=. sin x+cos xsin x-cos x1222cos45︒=.7、如图:一棵大树的一段B C被风吹断,顶端着地与地面成300角,顶端着地处C与大树底端相距4米,则原来大树高为_________米.8、已知直角三角形的两直角边的比为3:7,则最小角的正弦值为_______.9、如图:有一个直角梯形零件ABCD、AD∥BC,斜腰DC的长为10cm,∠D =120°,则该零件另一腰AB的长是__________cm.sinx+2cosx10、已知:tanx=2,则=____________.二、选择题1、在△R t ABC中,∠C=90°,a=1,c=4,则sinA的值是()1115B. C. D.2、已知△ABC中,∠C=90°,tanA·tan50°=1,那么∠A的度数是()1)° D.()°3、已知∠A+∠B=90°,且cosA=,则cosB的值为()5555A.c=α·sinAB.c=αC.c=α·cosBD.c=5、如果α是锐角,且cosα=,那么sinα的值是()255525A.3B.300C.D.150AD=1031514262A. B. C. D.4、在Rt△ABC中,∠C=90°,已知a和A,则下列关系式中正确的是()αsinA cosA4594316A. B. C. D.6、1米长的标杆直立在水平的地面上,它在阳光下的影长为0.8米;在同一时刻,若某电视塔的影长为100米,则此电视塔的高度应是() A.80米 B.85米 C.120米 D.125米7、化简(1-sin50°)2-(1-tan50°)2的结果为()A.tan50°-sin50°B.sin50°-tan50°C.2-sin50°-tan50°D.-sin50°-tan50°8、在Rt△ABC中,∠C=90°,tan A=3,AC等于10,则△SABC等于()503三、答题(本大题共4个小题,每小题7分,共28分)1、计算tan60°-tan45°1+tan60°·tan45°+2sin60°△2、如图,在ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,3cm,求∠B,AB,BC.3、甲、乙两楼相距50米,从乙楼底望甲楼顶仰角为60°,从甲楼顶望乙楼顶俯角为30°,求两楼的高度,要求画出正确图形。
第25章 解直角三角形单元检测题(含答案)-

第25章 解直角三角形单元检测题(答题时间90分,满分100分)一、选择题(第1-6小题每小题2分,第7-10小题每小题3分,共24分) 1.如果α是等边三角形的一个内角,那么cosα的值等于( )1..1222A B C D2.已知在Rt △ABC 中,∠C =90°.若sin A =22,则sin B 等于( ) A.21B.22C.23D.13.在Rt ABC △中,90C ∠=,下列各式中正确的是( ). A.sin sin A B = B.tan tan A B = C.sin cos A B = D.cos cos A B =4.如图,两条宽度均为40 m 的公路相交成α角,那么这两条公路在相交处的公共部分(图中阴影部分)的路面面积是( ) A.αsin 1600(m 2) B.αcos 1600(m 2) C.1600sin α(m 2) D.1600cos α(m 2) 5.△ABC 中,∠A 、∠B 都是锐角,且sin A =21,cos B =23,则△ABC 的形状是( )A.直角三角形B.钝角三角形C.锐角三角形D.不能确定 6.令a =sin60°,b =cos45°,c =tan30°,则它们之间的大小关系是( )A.c <b <aB.b <c <aC.b <a <cD.a <c <b7.在Rt △ABC 中,∠C =90°,下列式子中不一定成立的是( )A.tan A =AAcos sin B.sin 2A +sin 2B =1 C.sin 2A +cos 2A =1 D.sin A =sin B8.身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300 m ,250 m ,200m ;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝( )A.甲的最高B.乙的最低C.丙的最低D.乙的最高 9.如图4,为了测量一河岸相对两电线杆A 、B 间的距离,在距A 点15米的C 处 (AC ⊥AB )测得∠ACB =50°,则A 、B 间的距离应为( ) A.15sin50°米B.15tan50°米C.15tan40°米D.15cos50°米10.如图,客轮在海上以30km/h 的速度由B 向C 航行,在B 处测得灯塔A 的方位角为北偏东80,测得C 处的方位角为南偏东25,航行1小时后到达C 处,在C 处测得A 的方位角为北偏东20,则C 到A 的距离是( ) A. B.C.kmD.km二、填空题(第11-16小题每小题2分,第17-20小题每小题3分,共24分)11.如图表示甲、乙两山坡情况,其中t a n a _____t a n β,_____坡更陡.(前一空填“>”“<”或“=”,后一空填“甲”“乙”)αβ 1213 34甲乙12.在△ABC 中,∠C =90°,BC =3,AB =4.则∠B 的正弦值是_____.北(第10题图)13.小明要在坡度为53的山坡上植树,要想保证水平株距为5 m ,则相邻两株树植树地点的高度差应为_____m.14.已知α是锐角,且2cos α=1,则α=______;若tan(α+15°)=1,则tan α=______. 15.在直角三角形ABC 中,∠A=090,AC=5,AB=12,那么tan B = . 16.如图,B 、C 是河岸边两点,A 是对岸岸边一点,测得∠ABC =45°,∠ACB =45°,BC =60 m ,则点A 到对岸BC 的距离是_____m.17.要把5米长的梯子上端放在距地面3米高的阳台边沿上,猜想一下梯子摆放坡度最小为______.18.某人在20米高的塔顶测得地面上的一点的俯角是60°,这点到塔底部的距离约为______.(精确到0.1米)19.如图,机器人从A 点,沿着西南方向,行了个42单位,到达B 点后观察到原点O 在它的南偏东60°的方向上,则原来A 的坐标为 (结果保留根号). 20.升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为30°,若双眼离地面1.5米,则旗杆的高度为___________________米.(用含根号的式子表示) 三、解答题(本大题52分) 21.计算或化简:(1)3cos30°+2sin45°; (2)︒︒︒sin60cos60tan45-·tan 30°;22.根据下列条件,求出Rt △ABC (∠C =90°)中未知的边和锐角.(1)BC =8,∠B =60°. (2)∠B =45°,AC =6.23.如图,小刚面对黑板坐在椅子上.若把黑板看作矩形,其上的一个字看作点E ,过点E 的该矩形的高为BC ,把小刚眼睛看作点A .现测得: 1.41BC =米,视线AC 恰与水平线平行,视线AB 与AC 的夹角为25,视线AE 与AC 的夹角为20.求AC 和AE 的长(精确到0.1米)(参考数据:sin 200.34≈,cos 200.94≈,tan 200.36≈,sin 250.42≈,cos 250.91≈,tan 250.47≈.)24.如右图,某货船以20海里/小时的速度将一批重要的物资由A 处运往正西方向的B 处,经16小时的航行到达,到达后便接到气象部门通知,一台风中心正由A 向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.在B 处的货船是否会受到台风的侵袭?说明理由.西B北60AC1.41米ACEB水平线25.下表是小亮同学填写实习报告的部分内容:题 目在两岸近似平行的河段上测量河宽测量目标图示AB CDE测得数据 AB =15米,∠DBC =45°,∠ACB =15°,∠BDC =90°请根据以上的条件,计算出河宽CD .(结果精确到0.1米)26 如图,为测河宽,小丽在河对岸岸边任意选取一点A ,再在河这边B 处观察A ,此时视线BA 与河岸BD 所成的夹角为600;小丽沿河岸BD 向前走了50米到CA 与河岸BD 所成的夹角为450.根据小丽提供的信息能测出河宽吗?若能,请写出求解过程;若不能,请说明理由.(结果精确到1米)27.如图,要测量小山上电视塔BC 的高度,在山脚下点A 测得:塔顶B 的仰角为40BAD =∠,塔底C 的仰角为29CAD =∠,200AC =米.求电视塔BC 的高(精确到1米)(参考数据:sin 400.64≈,cos 400.77≈,tan 400.84≈,sin 290.48≈,cos 290.87≈,tan 290.55≈.)BDA C参考答案一、精心选一选1.A 2.B 3.C 4.A 5.B 6.A 7.D 8.D 7.B 10.D 二、耐心填一填; 11.< 乙 12.47 13.3 14.60°33 15.12516.30 17.43 18.320≈11.5(米) 19.(0,4+) 20.(83+1.5)米 三、用心解一解. 21.(1)25 (2)3122.(1)∠A =30° AB =16 AC =83.(2)∠A =45° BC =6 AB =23. 23.解:(1)在Rt ACB △中,tan BCBAC AC=∠, 1.413.0tan 0.47BC AC BAC =≈=∠(米)(写3不扣分). (2)在Rt ACE △中,cos ACEAC AE=∠,3.03.2cos 0.94AC AE EAC =≈≈∠(米). 24.解:AB =16×20=320(海里),作BD ⊥AC 垂足为D . ∵∠BAC =30°,∴sin30°=ABBD,BD =AB ·sin30°=160. ∵160<200,∴B 处的货船会受到影响.25.C D ≈35.5(米). 26.能测出河宽过点A 作 AE ⊥BC ,垂足为E ,设河宽为X 米. 在Rt △AEB 中,tan ∠ABE=BEAE∴BE =ABE AE tan =33在Rt △AEC 中 , ∵∠ACE=45° ∴EC = AE = x ∵ BE + EC =BC ∴ 33x + x = 50 ∴ x ≈ 32 (米) 答:河宽约为 32 米.27.解:在Rt ADC △中,90ADC =∠,29CAD =∠,200AC =.cos 2000.87174AD AC CAD =≈⨯=∠. sin 2000.4896CD AC CAD =≈⨯=∠.在Rt ADB △中,90ADB =∠,40BAD =∠,174AD =.tan 1740.84146.16BD AD BAD =≈⨯=∠.146.169650.1650BC BD CD ∴=-=-=≈(米).。
九年级数学上册 第25章解直角三角形单元测试 华东师大版

华东师大版初中九上第25章解直角三角形单元测试(90分钟 100分)一、选择题(每小题3分,共30分)1.在△ABC 中,∠C=90°,∠B=2∠A ,则cosA 等于 ( ) A .23 B .21C .3D .332.如图25—1,已知梯形ABCD 中,AD//BC ,∠B=45°,∠C=120°,AB=8,则CD 的长为 ( ) A .368 B .64 C .328 D .243.△ABC 中,∠C=90°,cosB=54,则AC :BC :AB 等于 ( ) A .3:4:5 B .4:3:5 C .3:5:4 D .5:3:44.如图25—2,河对岸有铁塔AB ,在C 处测得塔顶A 仰角为30°,向塔前进14 m 到达D ,在D 外测得A 的仰角为45°,塔高AB 为 ( ) A .)14316(-m B .)737(+m C .)7316(+mD .)7310(+m5.在△ABC 中,∠C=90°,若cos A=35,则sin B 等于 ( ) A .35 B .55 C .33 D .326.有一拦水坝横断面是等腰梯形,它的上底长为6 m ,下底长为10 m ,高为2 m ,那么此拦水坝斜坡的坡度和坡角分别是 ( )A .︒60,3B .︒30,3C .︒45,1D .︒45,3 7.已知cotA=3,∠A 为锐角,则cosA 的值为 ( ) A .21B .22C .23D .338.身高相同的甲、乙、丙三人放风筝,各人放出线长分别为300 m 、250 m 、200 m ,线与地面所成的角度分别为30°、45°、60°(假设风筝是拉直的)三个人所放风筝中 ( ) A .甲的最高 B .乙的最高 C .丙的最高 D .丙的最低9.在△ABC 中,若∠A=30°,∠B=45°,AC=8,则BC 的长为 ( ) A .4 B .24 C .34 D .6410.如果等腰三角形的底角为30°,腰长为6 cm ,那么这个三角形的面积为 ( ) A .4.5 cm 2 B .2cm 39C .2cm 318D .2cm 36二、填空题(每题3分,共18分)11.化简=︒-︒-⎪⎭⎫ ⎝⎛-︒|30sin 60tan |2145cos 2_________。
解直角三角形章节检测题.doc
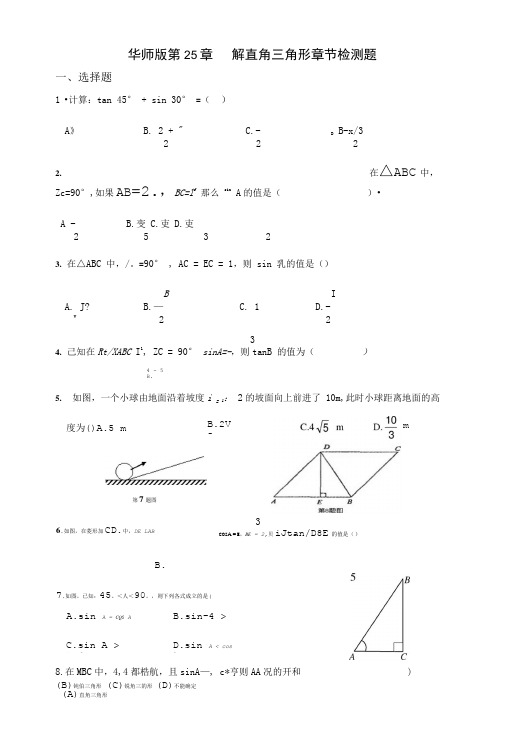
4 -5 B.度为()A.5 mB.2V 56.如图,在菱形加CD.中,DE LAB3COS A = E ,BE = 2,贝iJtan/D8E的值是( )B.27.如图,已知:45。
<人<90。
,则下列各式成立的是(A.sin A = CQS AB.sin-4 > cosC.sin A >tan AD.sin A < cosA8.在MBC 中,4,4都梏航,且sinA —, c*亨则AA 况的开和 )(B)钝伯三角形 (C)锐角三的形 (D)不能确定 (A)直角三角形华师版第25章 解直角三角形章节检测题一、选择题1 •计算:tan 45° + sin 30° =( ) A 》B. 2 + "C.- DB-x/32222.在△ABC 中,Zc=90°,如果AB =2.,BC=l f 那么 sin A 的值是( )•A - B.变 C.吏 D.吏25 323. 在△ABC 中,/。
=90° , AC = EC = 1,则 sin 乳的值是()B I A. J?B.—C. 1D.- V2234. 己知在Rt/XABC I 1, ZC = 90° sinA=-,则tanB 的值为()5. 如图,一个小球由地面沿着坡度i = 1: 2的坡面向上前进了 10m,此时小球距离地面的高第7题图m(C) 20 米(D)22 米D 久0 、z 0 w0 -V 0 \ \□ 0□LJ LJ10.如图,客轮在海上以30km/h 的速度由B 向C 航行,在B 处测得灯塔A 的方位角为北(A)(b)-T(C)W(D) -V3落在8C 边上,(A)l 3 折痕为BD,则sin ADBE 的值为( )(C )3^73739.如图,两建筑物水平距离为32米,从点4测得对点C 的俯角为30°,对点D 的俯角为45。
,则建筑物CD 的高约为().(A)14米(B)17米偏东80',测得C 处的方位角为南偏东25°,航行1小时后到达。
2021华东师大版九年级 数学上册第25章《解直角三角形》水平测试题及答案 (4) B

第25章 整章水平测试 班级 学号 姓名 分数一、选择题(每小题4分,共28分)1.在ABC ∆中,︒=∠90C ,AB=15,sinA=13,则BC 等于( ) A 、45 B 、5 C 、15 D 、1452.如图1,点P (3,4)是∠α的边OA 上的一点,则Sin α= .A 、35B 、45C 、34D 、43 3.如图2,在平面直角坐标系中,直线AB 与x 轴的夹角为60°,且点A 坐标为(- 2,0),点B 在x 轴上方,设AB=a,那么点B 的横坐标为( )A.2-2a ;B.2+2a ;C.-2-2a ;D.-2+2a 4.若1)10tan(30=+α,则锐角α的度数为( )A .200B .300C .400D .5005.正方形网格中,AOB ∠如图3放置,则sin AOB ∠=( )A.55 B.255C.12 D.2 6.在Rt △ABC 中,∠C=90°,已知α和A ,则下列关系式中正确的是( )(A )c=a ·sinA (B )c=A a sin (C )c=a ·cosA (D )c=Aa cos 7. 如图4,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60度500m 处,那么水塔所在的位置到公路的距离AB 是( ). A.250m B.2503m C.50033m D.2502m.8. 如图5,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60度500m 处,那么水塔所在的位置到公路的距离AB 是( ). A.250m B.2503m C.50033m D.2502m.AB O 第5题图 AO B 东 北二、填空题(每小题3分,共24分)9.在△ABC 中,∠C =90°,1,2==b a ,则=A cos tan ______=B10.Rt △ABC 中,,900=∠C 35tan ,3==B BC ,那么.________=AC 11.在△ABC 中,AB=AC=10,BC=16,则tanB=_____。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第25章解直角三角形检测试题
时间:60分钟 等级
将所选选项的字母写在题后的括号中
1.在△ABC 中, AB =5,AC =4,BC=3则sinA 的值是( )。
A .53
B .54
C .35
D .4
3
2.已知α为锐角,且3tan(α+100
)=1,则α的度数为( )。
A .30°
B .45°
C .20°
D .35° 3.在正方形网格中,△ABC 的位置如图所示,则
tan B ∠的值为( )。
A .1
B .3
C .
3
2
D .
33
4.已知Rt △ABC 中,∠C =90︒,tanA=3
1
,且AC=33,则BC 的值
为( ).
A .43
B .83
C .4
D .3
5一辆汽车沿倾斜角是α的斜坡行驶500米,则它上升的高度是()
A.500sin α米
B.500sin α米
C.500cos α米
D.500
cos α
米
6.下列说法中,正确的是( ) A.sin600+cos300=1.
B.若α为锐角,则2)1(sin -α﹦1﹣sin α.
C.对于锐角β,必有sin cos ββ<.
D.在Rt △ABC 中,∠C =90︒,则有tan cot A 7.如图,是一个中心对称图形,A 为对称中心,若∠C=90°, ∠B=30°,BC=1,则
BB ′的长为( ). A .4 B .33 C .3
32
第3题图
第7题图
30°
A
C
B ′ B
C ′
D .
3
3
4 8.下列各式中正确的是( ) A sin300+cos600=1 B sinA=
2
1
=300 C cos600=cos(2×300 )=2cos300 D tan600+cot450=23 9.当锐角A >300时,cosA 的值是( )
A 小于21
B 大于2
1
C 小于23
D 大于23
10.等腰三角形一腰上的高线为1,且高线与底边的夹角的正切值为
1,则这个等腰三角形的面积为( )。
A 2
1
B 1
C 23
D 3
11.如图,在某海岛的观察所A 测得船只B 的俯角是300 ,若观察
所的标高(当水位是0米时的高度)是53米,当时的水位是+3米,则观察所A 和船只B 的水平距离是( )米。
A 50 B 503 C 53 D 533
12.如图,Rt △ABC 中, ∠C =90︒,
AC BC =, 点D 在AC 上,30CBD ∠=︒,则AD
DC
的值为( ) A .3 B .2
2
C .31-
D .不能确定
第12题图
13. 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°看这栋楼底部的俯角为60°,热气球与高楼的水平距离为120米,这栋楼的高度的应为( )
A .403
B .
1203 C .1603 D .803
14.直角三角形纸片的两直角边长分别为6和8,现将ABC △如图那样折叠,使点A 与点B 重合,折痕为DE ,则tan CBE 的值是 A .
247
B .
7 C .
724 D .1
3
( )
15.如图所示,晓阳发现电线杆AB 的影子落在土坡的坡面CD 和地面BC 上,量得CD=8米,BC=20米,CD 与地面成300,且此时测得1米杆的影长为2米,则电线杆的高度为( )
A 9米
B 28米
C (7+3)米
D (14+23)米
6 8 C
E
A
B D 第14题图
二、填空题:请把下列各题的正确答案填写在横线上
16.若关于x 的方程22cos 0x x α-+=有两个相等的实数根,则锐角α为
17.在等腰△ABC 中,AB=AC=3,BC=2,则cosB 的值为
18.如图所示,某河堤的横断面是梯形ABCD ,BC AD ∥,迎水坡AB 长13米,且斜坡AB 的坡度为12
5
,则河堤的高BE 为 米. 19. 等腰三角形的顶角是1200 ,腰长是43cm, 则 这个三角形底边上的任意 一点到两腰的距离
之
和是
20.在方格纸中,每个小格的顶点为格点,以格点连线为边的三角形叫做格点三角形.在如图所示的5×5的方格纸中,作格点△ABC 与△OAB 相似,(相似比不能为1),则C 点的坐标为
三、解答题:解答应写出必要的计算过程、推演步骤或文字说明 21.计算:(1)cos601
1sin 60tan 30︒+
+︒︒
(2)()()4sin 30tan 60cot 304cos 60-+
B
C D E A 第13题图 第15题图
22.如图,在△ABC 中,∠C =90°,sin B =
5
3,AB =15,求△ABC 的周长和tan A 的值.
23.如图,在直角坐标系中,P 是第一象限的点,其坐标是(),8x ,
OP 与x 轴的正半轴的夹角为α,且4tan 3
α=,求:
(1)x 的值; (2)角α的余弦值
24.一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处.这时,海轮所在的B处距离灯塔有多远(精确到0.1海里)?参考数据cos250.906
︒≈,︒≈
sin340.56
第25章解直角三角形参考答案及评分标准
一、每题3分,共45分
1—5ACADA 6---10BDACA 11—15BCCCD 二、每题3分,共15分
16. 600 17. 1
3
18.12 19.6cm. 20.(5,2)
三、每题12分,共60分
21. 每题5分,共10分(1)2(2)、1
22.解:在△ABC 中,因为∠C =90°,sin A =
5
4
,所以BC=12,---------3分
又因为AC 2+BC 2=AB 2 所以BC=9-----------5分
△ABC 的周长为:AC+BC+AB=9+12+15=36--------8分
-----------------10分
23.解:连结OP ,过P 作PH ⊥x 轴于H
在△OPH 中,PH=8,4
tan 3
α=,所以OH=6,即x=6--------5分
又因为PH=8,OH=6,所以OP=10----------8分
-----------10分
24.过点P 作PH ⊥AB 于H 。
在Rt △APH 中,∠APH=250,PH=APcos250-----2分 在Rt △BPH 中, ∠PBH=340,PB=PH/ sin340-----7分 PB= APcos25/ sin340=129.4海里。
-------9分 答:-----------10分。
