挠曲线方程
挠曲线的近似微分方程

Tmax 180 [] GIp
一般传动轴, [φ’] = 0.5 ~1/m
例4 图为一圆截面轴 AC ,受扭转力偶矩MA,MB 与Mc作用。 已知MA =90 N·m , MB =160 N·m , MC =70 N·m , l=2 m, G=80 GPa , IP=3.0×105 mm4 , [φ’] =0.3 (o)/m 。试计算 该轴的总扭转角 φAC (即截面C对截面A的相对转角),并 校核轴的刚度。
u x
ab线段的平均正应变
lim u ab0 x
a △x b△ub’
a点沿ab方向的正应变
正应变特点:
• 正应变是无量纲量; • 过同一点,不同方位的正应变一般不同。
2、切应变
b b’ a
直角bac的改变量——直角bac的切应变
tan
lim
ba 0
Bx FBy
解:弯矩方程 :
M x 1 qlx 1 qx2
22
挠曲线的近似微分方程:
w
1 EI z
1 2
qlx
1 2
qx2
进行一次积分得:
w
1 EI z
1 4
qlx2
1 6
qx3
C
再进行第二次积分得:
w
1 EI z
1 12
qlx3
三、应变 构件的形状是用它各部分的长度和角度来表示。因此
构件的变形也可以归结为长度的改变和角度的改变,即
线变形和角变形。
棱边长度改变
棱边夹角改变
b’ b
材料力学课件ppt-6弯曲变形

L 6
(x
a)3 ]
4、求转角
x 0 代入得:
A
1
x0
Fb(L2 b2 ) 6LEI
x L代入得:
B
2
xL
Fab(L 6LEI
a)
目录
5、求 ymax 。
由 dy 0 求得 ymax 的位置值x。
dx
A
Fb(L2 b2 ) 6LEI
0,
C
1
xa
Fab(a b) 3LEI
0( a
例6-4 已知:q、l、 EI,求:yC ,B
目录
w w w
目录
弯曲变形/用叠加法求梁的变形 w
B1
ql3 24 EI
,
wC1
5ql 4 384 EI
w
B3
(ql2 ) l 3EI
ql3
3EI
,
wC 3
3ql 4 48 EI
w
B2
(ql) l2 16 EI
ql3 16 EI
,
wC 2
(ql )l 3 48 EI
则简支梁的转角方程和挠度方程为
AC段 (0 x a)
1(x)
Fb 6LEI
[3x2
(L2
b2
)],
y1 ( x)
Fb 6LEI
[x3
(L2
b2 )x],
BC段 (a x L)
2 ( x)
Fb 6LEI
[3x2
(L2
b2 )]
F(x 2
a)2
,
y2
(x)
Fb 6LEI
[x3
(L2
b2)x
目录
§6-4 用叠加法求弯曲变形 一、叠加法前提
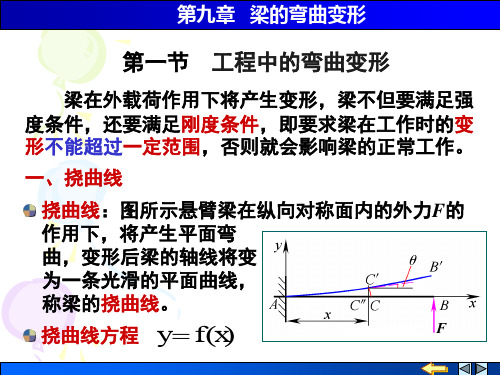
第九章梁的弯曲变形
a xl
在 x l / 2处
y 0.5l
Fb
(3l 2 4b 2 ) 48 EI
yqx(l32lx2x3) 2E 4 I
A
B
ql3 24EI
x
l 2
ymax
5ql4 384EI
梁的简图
第九章 梁的弯曲变形
挠曲线方程
y6M EI(xllx)2(lx)
yC1
aB
qa4 2EI
yC2
qa4 8EI
3)叠加 y C y C 1 y C 2 2 q E 4a 8 I q E 4a I 5 8 q E 4( a I)
第九章 梁的弯曲变形
例9-5 悬臂梁跨度为 l =2m,截面为矩形,宽b = 100mm,高h =120mm,材料的弹性模量E=210GPa, 梁上载荷如图所示,求自由端A的挠度。
挠曲线方程 y f (x)
第九章 梁的弯曲变形
二、挠度和转角
挠度:截面形心线位 移的垂直分量称为该 截面的挠度,用 y 表 示,一般用 ymax 表示 全梁的最大挠度。
转角:横截面绕中性轴转动产生了角位移,此角
位移称转角,用 表示。小变形时,转角 很小,
则有以下关系:
tanydy
1
(x)
M(x) EI
曲线 y f(x)的曲率
1
(x)
(1yy2)3/2
二阶小量
y (1y2)3/2
M(x) EI
挠曲轴线 近似微分方程
y M(x) EI
第九章 梁的弯曲变形
挠曲轴线 近似微分方程
y
挠曲线
主要内容及重点:计算弯曲变形的积分法、叠加法弯曲刚度计算梁的超静定问题1.弯曲变形工程中的弯曲变形问题2.1、挠曲线OB—平面弯曲时,梁变形后轴线。
在xoy 平面内的一条连续、光滑的弹性曲线。
PyxBA(梁弯曲变形的两个基本量)(1)挠度:梁变形后,横截面的形心在垂直于梁轴线(x 轴)方向上所产生的线位移,称为梁在截面的挠度。
一般情况下,不同横截面的挠度值不同。
横截面挠度随截面位置(x 轴)而改变的规律用挠曲线方程表示。
即:)(x f y =y AP x由梁弯曲的平面假设可知:梁的横截面变形前垂直于轴线,变形后仍垂直于挠曲线。
:曲线OAB 在A 点的切线与X 轴间的夹角θABAy AP xθA)挠度与转角的关系挠曲线切线的斜率:θtg dxdy=工程中θ极小:θθtg ≈)(x f dy′==θzEI M =ρ1zEI x M x )()(1=ρOBPyxBPx23222])d d (1[d d )(1xw x w x +±=ρz EI x M xw x w)(])d d (1d d 23222=+zEI x )(ρzEI x M x w )(d d 22=±zEI x M x w )(d d 22=±o>0d 2M>0d 2d 2<0oM<02d zEI Mx w =22d d -挠曲线近似微分方程线弹性范围适用对于等直梁)(x M x w EI z =22d d Cx x M xwEI x EI z z +=∫d )(d d )(=θDCx x x x M x w EI z ++=∫∫d d )()(C 、D :积分常数边界条件已知的挠度及转角光滑连续性PM(x)=F P (L-x)xF L F x L x M xwP P 22))(d −=−=DCx x F x F ++−=3P 2P 6121)θA =0 x =0 时w A =0C=0 D=0)()(x L EI xF x z −22P =θ)3(6)(2P x L EI xF w z−=θEI LF 22P max =θL F w 3P =Pmaxm a xθC x F Lx F x EI P Z +−==2P 21)(θmaxy maxB θ解:建立坐标、写弯矩方程)段:(20lx AC <≤)段:(l x lCB ≤<2BCL/2L/2xxPxx 21)(=)2(21)(lx P Px x M −−=Px1)=)(1)(lx P Px x y EI −−=′′一次:利用边界条件确定积分常数:12141C Px EI Z +=θ1131121D x C Px y EI Z ++=2222)2(241C l x P Px EI Z +−−=θ22332)2(6121D x C l x P Px y EI Z ++−−=⇒==右左右左,C C C C y y θθ2121DDC C ==2100D D y x A =⇒==,02Pl C C y l x B −==⇒==,maxy maxB θBCpL/2164Z 224EI Z )1612(23x Pl Px Z −]16)2(6121[12332x Pl l x P Px EI y Z −−−=max0θ,,l x ==ZEIPl 162max∓=θmax2y lx ,=ZEIPl y 483max−=maxy maxB θBCpx思考:在用积分法求梁的转角和位移过程中,何时需要考虑静力关系、物理关系、变形协调关系?静力关系:支反力、弯矩计算物理关系:挠曲线近似微分方程变形协调关系:积分运算及边界条件图示纯弯曲悬臂梁的挠曲线应为一圆弧线,而由积分法求得的梁挠曲线为二次抛物线为什么?近似微分方程获得的梁挠曲线近似解自由端B 处挠度的精确解:EIxM v e 22=()+−=⎟⎟⎠⎞⎜⎜⎝⎛+−=−=43242!4!2cos 1lM l M v e e BBB θθρθρ1222211)()()(a x m x Lm x M x L mx M −−==2a a 2a x2()2)(452)(2)(222222211a x q a x qa x q x M x q x M −+−+−−==5.用叠加法求弯曲变形叠加法:当梁上同时作用几个荷载时,在小变形情况下,且梁内应力不超过比例极限,则每个荷载所引起的变形(挠度和转角)将不受其它荷载的影响。
用积分法求挠度和转角

挠曲线的近似微分方程为
d 2 w q (x 2 lx) dx 2 2EI
2) 对微分方程进行积分并确定积分常数。 对挠曲线近似微分方程
积分得
q ( x3 lx2 ) C
2EI 3 2
w q ( x4 lx3 ) Cx D 2EI 12 6
简支梁在铰支座处的挠度均为零,即
x=0,w=0; x=l,w=0
1 M (x) ρ(x) EI
由高等数学可知,平面曲线w = w(x)上任一点的曲率为
目录
弯曲变形\用积分法求挠度和转角
d2w
1 dx 2
(x)
[1
(
dw
)
2
]
3 2
dx
在小变形条件下,转角是一个很小的量,故 (dw)2 << 1,于是
上式可简化为
dx
1 ρ(x)
d2w dx2
d2w dx2
由于梁的支承和受力对称于梁跨中点,因而梁的挠曲线应为一
对称于梁跨中点的下凸曲线。因此,梁的最大挠度发生在跨中点截
面C (x=l/2)处,其值为
wmax
wC
5ql4 384EI
目录
弯曲变形\用积分法求挠度和转角
最大转角发生在支座A (或支座B )处,其值为
max
A
ql3 24EI
()
目录
弯曲变形\用积分法求挠度和转角 【例6.3】 图示简支梁在C点处受集中力F作用,试求梁的挠曲
说明横截面B的形心向下移动。
目录
弯曲变形\用积分法求挠度和转角 【例6.2】 图示简支梁AB,受均布荷载q作用。求梁的挠曲线方
程和转角方程。并计算梁的最大挠度和最大转角。设弯曲刚度EI为 常数。
挠曲线近似微分方程

C1
Fb 6l
l2 b2
,
C2
Fab 6l
l
a
Page 14
材料力学 第六章 弯曲变形
四 积分法总结
❖ 优点:适用范围广、精确 ❖ 缺点:计算繁琐
五 刚度条件
w
max ቤተ መጻሕፍቲ ባይዱax
w
练习:写边界条件和连续性条件
A
B
C
D
边界条件 wA 0; wB 0
连续性条件 wC wC;C C 或wC' wC' wD wD;D D 或wD' wD'
Mi EI wi" M EIw" M
w
wi
Page 19
材料力学 第六章 弯曲变形
例一:求图示简支梁C点挠度
y A
l/2
F
C l/2
x B
=
y
y
F
A
C
+ x
B
A
x
C
B
l/2
l/2
l/2
l/2
wC
wC q
wC F
5ql4 384EI
Fl 3 48EI
材料力学 第六章 弯曲变形
Page 20
Page 16
材料力学 第六章 弯曲变形
练习(续)
y
a
x
b
l
边界条件 w 0; 0
x0
x0
连续性条件
w w ;
w w ;
xa
xa xa
xa
xb
xb xb
xb
Page 17
材料力学 第六章 弯曲变形
一 叠加§原理6.4 用叠加法求梁的变形
材料力学第五章梁弯曲时的位移

工程实例
7-1
工程实例
工程实例
5-1 梁的位移——挠度及转角
建立坐标系,oxy为梁对称面,外力作用在对 称面内。所以,挠曲线为o xy面内的平面曲线。
挠度
y 向下为正。
y
x
y
转角
x
挠曲线
挠曲线方程:
7-2
w= f (x)
挠度
略去剪力的影响,则平面假设成立,发
y
5.2 积分法求梁的挠度和转角
例1 求梁的转角方程和挠度方程,并求最大转角和最大挠度, 梁的EI已知。
解 1)由梁的整体平衡分析可得:
2)写出x截面的弯矩方程
FAx 0, FAy F (), M A Fl (
)
A
x
l
yB
F B
B
x
M ( x ) F (l x ) F ( x l )
A
FAx 0, FAy
Fb Fa , FBy l l
2)弯矩方程
FAy x1
ymax
x2
FBy
AC 段:
M x1 FAy x1 Fb x1 ,0 x1 a l
y
a
b
CB 段:
Fb M x2 FAy x2 F ( x2 a ) x2 F ( x2 a ), l
目录
a x2 l
5.2 积分法求梁的挠度和转角
A d 2 w1 Fb EI M ( x1 ) x1 2 dx1 l FAy x1 dw1 Fb 2 EI EI ( x1 ) x1 C1 x2 dx1 2l Fb 3 a EIw1 x C1 x1 D1 6l a x2 l CB 段: y d 2 w2 Fb EI M ( x2 ) x2 F ( x2 a) 2 dx2 l dw Fb 2 F EI 2 EI ( x2 ) x 2 ( x2 a ) 2 C 2 dx2 2l 2 Fb 3 F EIw2 x 2 ( x2 a)3 C2 x2 D2 6l 6
材料力学-弯曲变形

二、叠加法求梁的变形 梁的刚度校核
1. 叠加法求梁的变形
当梁上同时受几种荷载作用时,我们可用叠加法来计算 梁的变形。其方法是:先分别计算每一种荷载单独作用时所 引起的 梁的变形(挠度或转角),然后求出各种荷载作用下 变形的代数和,即得到这些荷载共同作用下的变形。一般工 程中要找的是特定截面的变形(最大挠度和最大转角)。我 们将一些简单荷载作用下梁变形的计算公式列成教材中表81,以供选用。
2
式(8-2)再积分一次得:
y
1 EI
M( x)dxdx
Cx
D 8
3
式(8-2)、(8-3)为转角方程和挠曲线方程。式中常数C、D
可由边界条件确定。
图8-1a 图8-1b
(图8-1a)的边界条件为:
x 0, yA 0; x l, yB 0
(图8-1b)的边界条件为:
x 0, yA 0;
ql 3 24EI
, B
ql 3 24EI
转角 A 为负值,表明A截面绕中性轴作顺时针方向转动; 转角 B 为负值,表明B截面绕中性轴作逆时针方向转动。
例2:试计算图示梁的转角方程和挠曲线方程,并求 ymax
例2图
设:a>b
解:(一)分段建立弯矩方程和挠曲线近似微分方程并积分二次
AC 段 (0 x1 a)
C1a D1 C2a D2 将 C1 C2, D1 0 代入上式得:D1 D2 0
将 D2
0 代入式e得:C2
Pbl 6
P(l a)3 6l
化简后得:
C1
C2
Pb 6l
(l 2
b
2)
(三) 列出转角方程和挠曲线方程:将C1,C2, D1, D2代入式 a,b,c,d得:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.挠曲线方程——从图中我们可以看出:梁的轴线上每一点 的挠度y是随着点的位置x的改变而变化的,因此它是x的函数, 即:
y f x ——挠曲线方程
4.转角方程——由截面的平面假设可知:变形前垂直于轴线 的横截面,变形后仍垂直于挠曲线,故,当我们通过挠曲线上
§7-1 概述
*在上一章中,我们对各种截面梁中横截面上的应力,作 了比较详尽的介绍和分析,但是,对一根梁来说,它是不是只
要满足了应力要求,即强度条件,就能够使得整个构件正常,
安全的工作呢?为了回答这个问题,下面我们先看一看几个简 单的例子:
齿轮轴弯曲变形过大,就要影 响齿轮的正常啮合,加速齿轮 的磨损,产生较大的噪音。
任意一点C1作切线时,它与水平线的夹角 显然等于C1点所在 横截面的转角 ,于是:
挠曲线: y f x
任一点的斜率与转角之间的关系为: dy tg
dx
由于: 极其微小
tg
dy f ' x
dx
——转角方程
物理意义: 反应了挠度与转角之间的关系,即挠曲线上任意一点处切
二.讨论:
从(9-3)式可看到:在等式的右边有一个+号。到底是取 正号还是取负呢?
我们大家都知道,梁变形后的形状,不外乎<a><b>两种。 我们现在分别讨论:
<a>:在如图所示的坐标系中,显然 y'' 0 (因为 y'' 0 时,函数
出现极小值)而此时:M<0故,等式的右边应取“—”号, 即:
齿轮轴弯曲
吊车梁若变形过大,一方面会使 吊车在行驶过程中发生较大的振 动,另一方面使得吊车出现下坡 和爬坡现象。
吊车梁变形
* 从上面两个例子我们可看出:梁即使满足了强度条件,若变
形过大的话,它仍然不能够正常安全的工作。由此,我们可 以得出:要使梁正常安全的工作,一方面梁不仅要满足强度 条件,另一方面梁还必须满足一定的变形条件。只有在这两 方面同时得到满足的条件下,整个构件才能正常安全工作。
线的斜率等于该点处横截面的转角。
结论:由转角方程我们可看出:梁上某点处横截面的转角等于 f ' x 在该点处的大小。研究梁的变形的关键在于提出
挠曲线方程 y f x。
5.挠度,转角的正负号规定: 挠度:向下的挠度为正,向上的挠度为负 转角:顺时针的转向为正,逆时针的转向为负
目录
§7-2 梁的挠曲线近似微分方程用其积分
yC AC ,转角C AC应该与CB段上C点的 挠度 yC CB,
转角 C CB 相等,即:
yC AC yC CB
C AC C CB
分别或同时利用上述两种条件就可以将积分常数确定出来。
第九章的内容就告诉了我们上面所提到的梁所必须满足 的变形条件以及计算这种弯曲变形的方法,下面我们首先来 看几个基本概念:
举例:如图所示:取梁变形前的轴线为x 轴,与 x 轴垂直的 为y 轴。弯曲变形后,在 xy 平面内,AB——弧AC1B,挠曲 线——平面曲线AC1B。
F
A
By
x
C1
x
1.挠度——梁的轴线上某一个点在垂直于x轴的方向(y方向) 所发生的位移。
如果这两个常数不知道的话,我们还是无从求出 和y。
下面我们还要对C、D进行确定:
四.积分常数的确定:
一般情况下,积分常数可通过梁的支座处的变形条件(称 为边界条件或支承条件)或梁的挠曲线的变形连续性条件来确 定。 1.变形条件:所谓变形条件,一般是指梁的支承处的变形特点, 如铰支座及连杆支座处的挠度为零。固定端处的挠度为零。见 下图:
y '' M x
EI Z
y '' 0
<b>:在如图所示的坐标系中,显然,此时函数出现了极大值 而此时:M>0
故等式的右边应取“—”号,即:y M x
EI Z
综上所述,得出: y '' M x
EI Z
——挠曲线的近似微分方程
三.积分:
对等截面梁来说:I Z 常量 故(9-3)可写成:
本章要点
(1)梁绕曲线近似微分方程 (2)叠加法求梁变形 (3)简单静不定梁的求解
重要概念
挠度、转角、边界条件、连续性条件、变形比较法
目录
§7-1 概 述 §7-2 梁的挠曲线近似微分方程用其积分 §7-3 用叠加法求梁的变形 §7-4 简单静不定梁的解法 §7-5 梁的刚度校核及提高梁的刚度措施 §7-6 梁内的弯曲应变能
一.挠曲线近似微分方程(的推导)
在上一章,讨论纯弯曲变形时,得出:梁纯弯曲时轴 线的曲率为:
1 M K EI Z
(a)
在横力弯曲中,我们知道梁的横截面上的内力除弯矩外, 还有剪力,但同时我们又知道:工程上常用的梁,由 于L(跨长)远大于h(横截面高度),剪力的影响很小, 可忽略不计。故我们仍可将其当作纯弯曲梁来处理。有(a) 式来表示曲率大小。但由于在横力弯曲中,曲率和弯矩都 是x的函数。故而应写为:
A
B
yA 0
yB 0
A
B
yA 0
yB 0
yA 0
A 0
yA 0
A 0
2.连续性条件:指梁被载荷分成几段时,我们将分段列出弯矩 方程,由于梁的挠曲线是一光滑连续曲线,所以段与段之间连 接处的挠度,转角在两段上的数值必须相等。
例如:<b>中c点为AC段与CB段的连接点,则AC段上C点的挠度
EI Z y '' M x
积分得:
EIZ y'' M xdx C
(9-4)
EIZ y M xdxdx Cx D
(9-5)
由此我们可看出:根据(9-4)(9-5)就可以把某点处截 面的转角和挠度求出来。
但由(9-4)(9-5)我们还看到,有两个积分常数C、D。
1
x
M x
EI Z
Kx
(b)
又:
1
x
y
1 y2
3 2
1
x
y
M x
EI Z
1 x
EI Z
(9-3)
——挠曲线近似微分方程
注:上式之所以称为梁的挠曲线近似微分方程,主要是略去 了剪力的影响和 y2 项的结果。
