§6-2梁的挠曲线近似微分方程及其积分(精)
合集下载
梁的挠曲线近似微分方程及其积分.
f (P1P2 Pn ) f1(P1 ) f2 (P2 ) fn (Pn )
二、结构形式叠加（逐段刚化法）：
A a
P q
C a
P
a
a
q
a
a
+
=
例6－4-1 按叠加原理求A点转角 和C点挠度.
解、载荷分解如图
、由梁的简单载荷变形表，
查简单载荷引起的变形。
PA
Pa 2 4 EI
f ( x) M ( x) I0 M ( x)
EI ( x) I0
EI 0
EI 0 f ( x) M ( x)
M(x) M(x) I0
I(x)
：几何形状：长度不变，惯性矩变为I0 。
：实梁对应方程： EI0 f ( x) M ( x)
虚梁对应方程：
M (x) q(x)
：令：q(x) M ( x ) 依此建立虚梁上的分布载荷。
8
2
- q a2
a2
C
a
求虚梁B点的剪力和弯矩
x
13qa 3 RA 72
QB
13qa3 72
1 2
qa2 2
a
5 72
qa3
MB
13qa3 72
a
1 2
qa2 2
a
a 3
7 72
qa4
D
B
5qa 3 72EI
7qa4 f B 72EI
C点左右位移怎样？
四、变截面直梁的共轭梁法： ：将截面的变化折算到弯矩之中去。
梁的挠曲线微分:方E程 If ( x) M ( x) 梁的外载与内力的为关 : M系(x) q(x)
上二式形式相同，用类比法，将微分方程从形式上转化为 外载与内力的关系方程。从而把求挠度与转角的问题转化为求 弯矩与剪力的问题。
二、结构形式叠加（逐段刚化法）：
A a
P q
C a
P
a
a
q
a
a
+
=
例6－4-1 按叠加原理求A点转角 和C点挠度.
解、载荷分解如图
、由梁的简单载荷变形表，
查简单载荷引起的变形。
PA
Pa 2 4 EI
f ( x) M ( x) I0 M ( x)
EI ( x) I0
EI 0
EI 0 f ( x) M ( x)
M(x) M(x) I0
I(x)
：几何形状：长度不变，惯性矩变为I0 。
：实梁对应方程： EI0 f ( x) M ( x)
虚梁对应方程：
M (x) q(x)
：令：q(x) M ( x ) 依此建立虚梁上的分布载荷。
8
2
- q a2
a2
C
a
求虚梁B点的剪力和弯矩
x
13qa 3 RA 72
QB
13qa3 72
1 2
qa2 2
a
5 72
qa3
MB
13qa3 72
a
1 2
qa2 2
a
a 3
7 72
qa4
D
B
5qa 3 72EI
7qa4 f B 72EI
C点左右位移怎样？
四、变截面直梁的共轭梁法： ：将截面的变化折算到弯矩之中去。
梁的挠曲线微分:方E程 If ( x) M ( x) 梁的外载与内力的为关 : M系(x) q(x)
上二式形式相同，用类比法，将微分方程从形式上转化为 外载与内力的关系方程。从而把求挠度与转角的问题转化为求 弯矩与剪力的问题。
10.2 梁的挠曲线近似微分方程及其积分
10.2 梁的挠曲线近似微分方程及其积分纯弯曲 EIM =ρ1挠曲线曲率()322"1w w κ=⎡⎤'+⎣⎦EIM ±=d θFFxd xyxρ O正负号的确定xyOxyOM > 0w ″< 0M < 0w ″>0M 与 w ″异号()322"1w w κ=⎡⎤'+⎣⎦EIM ±=()3221w M EIw ''=-⎡⎤'+⎣⎦小变形：转角 w ′ ≈ 0 适用条件： 1. 坐标系，正负号；2. 忽略剪力 F S 对变形的影响；3. 线弹性，小变形，w′ ≈ 0。
M w EI''=-EI ——梁的抗弯刚度， 若为等直梁，EI ＝C ，则 EIw M''=-挠曲线近似微分方程1'd Mw x C EIθ==-+⎰12d d M w x x C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰一次积分：二次积分：积分法计算梁的变形BAlw A = 0 w B = 0BAlw A = 0 θA =0EIw M''=-挠曲线近似微分方程 由边界条件，确定积分常数光滑连续条件——相邻挠曲线必须光滑连续。
挠曲线近似微分方程及其积分w C2= w C3θC2=θC2w B1= w B2θB1=θB2挠曲线近似微分方程及其积分——例题[例题1] 已知悬臂梁的抗弯刚度为EI，求在荷载P 作用下梁的挠曲线方程，并确定梁上的最大挠度和转角。
BAxL P有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）[解] （1）建立弯矩方程 ()()M x P L x =-()()E Iw M x P L x ''=-=--21()2xEIw P Lx C '=--+2312()26Lx x EIw P C x C =--++（3）确定积分常数 0,0x w ==0,0x w '==20C=10C=挠曲线近似微分方程及其积分——例题BALxPx（2）代入挠曲线方程并积分挠曲线近似微分方程222PLx Pxw EIθ-'==-23(3)6P Lx x w EI-=-最大挠度和转角3max()3PL f EI=↑2max2PL EIθ=挠曲线近似微分方程及其积分——例题B ALxPxmaxθmaxw挠曲线近似微分方程及其积分——例题[例题2] 已知：EI = 常数，求：1. 挠度、转角方程； 2. |θmax |, |w max |。
概述梁的挠曲线近似微分方程及其积分用积分
x 0 时， ， wA 0 A w A 0
当
求得：
C 0; D 0
y
L
P
B
B
wB
x
写出挠曲线方程并画出挠曲线的大致形状
Px 2 w( x) ( x 3L) 6EI
最大转角及最大挠度（绝对值最大）
max
PL2 B （ ） 2 EI
wmax
PL3 wB （ ） 3EI
C
x1
x2
AB段 (0 x1 a)
a
a
M1 Px1
BC段 (0 x2 a)
M 2 P(a x2 )
写出挠曲线微分方程并积分 AB段
M1 Px1 EIw1
P 2 EI1 x1 C1 EIw1 2 P 3 EIw x1 C1 x1 D1 6
1
y
M<0
d2w 0 2 dx
d2w M ( x) 2 EI dx
o
x
d 2 w M ( x) (2) 2 EI dx
式（2）就是挠曲线近似微分方程。
对于等截面直梁，挠曲线近似微分方程可写成如下形式：
d w M ( x) 2 EI dx
二、求转角方程、挠曲线方程 1.微分方程的积分
最大挠度及最大转角
dw( x 2 ) Pa 2 ( x2 ) dx 2 2 EI
2
y
a
P
C
C
max C CB
wmax
Pa 2 2EI
L
B
x
wB
Pa 2 wB (3L a) 6EI
例2 求图示梁自由端的转角和挠度。
讲梁的挠曲线方程与积分解法
②积分常数的确定——边界条件和连续条件：
边界条件：梁在其支承处的挠度或转角是已知的， 这样的已知条件称为边界条件。 连续条件：梁的挠曲线是一条连续、光滑、平坦 的曲线。因此，在梁的同一截面上不可能有两个 不同的挠度值或转角值，这样的已知条件称为连 续条件。
边界条件
积分常数2n个=2n个
连续条件
列出图示结构的边界条件和连续条件。
8
代入（1）（2）得：
1 ( 1 qx3 1 qL3)
EI 6 6
1 ( 1 qx4 qL3 x qL4 )
EI 24
68
将 x 0 代入得：
A
qL3 6EI
（与C比较知E：I A C）
A
qL4 8EI
（与D比较知E：IA ）D
因此
常数C表示起始截面的转角×刚度(EI)
常数D表示起始截面的挠度×刚度(EI)
x L
2
2、
d 2
dx 2
M (x) EI z
EI" 1 qx2
2
积分一次： EI' EI 1 qx3 C （1）
积分二次：
6
EI 1 qx4 Cx D （2）
24
B X``
3、确定常数C、D.
由边界条件： x L, 0 代入（1）得： C 1 qL3
6
x L, y 0 代入（2）得： D 1 qL4
支座反力，分段列弯矩方程； 分段的原则:
①凡载荷有突变处（包括中间支座），应作为分段点；
②凡截面有变化处，或材料有变化处，应作为分段点；
③中间铰视为两个梁段间的联系，此种联系体现为两部分之间 的相互作用力，故应作为分段点；
(2)分段列出梁的挠曲线近似微分方程，并对其积分 两次
挠曲线近似微分方程及其积分
再积分一次，得挠度方程：
(x) 1 ( M(x)dx) cx D EI
2. 挠曲线近似微分方程及其积分
(2) 边界条件和连续条件 边界条件：梁在其支承处截面的挠度或转角是已知的，
这样的已知条件称为边界条件。
P D
固定端处 0 ， 0
P
A
C
B
铰支座处 0
M( x1 )
EI
x1
)
ql 2 8
EI ( x1 ) EI1 m( x1 )dx c1
ql 2 8
x1
c1
──── (1)
EI( x1）
EI1
M( x1)dx
dx
c1 x1
D1
ql 2 16
x12
c1 x1
D1
─ (2)
BC段： EI2
EI ( x2 )
d 2 M ( x)
dx2 EI
当y轴向上为正方向时，恒同号。
d 2
dx2
M(x) EI
——这个等式称为挠曲线近似微分方程。
2. 挠曲线近似微分方程及其积分
二、挠曲线近似微分方程的积分法
(1) 转角方程和挠度方程 对挠曲线的近似微分方程一次积分，得转角方程：
(x) d 1 ( M(x)dx c) dx EI
2. 挠曲线近似微分方程及其积分
连续条件：当弯矩方程需要分段建立时， 梁的挠曲线分段处满足的连续、光滑条件， 这样的已知条件称为连续条件。即在梁的 同一截面上应具有相同的挠度和转角。
2. 挠曲线近似微分方程及其积分
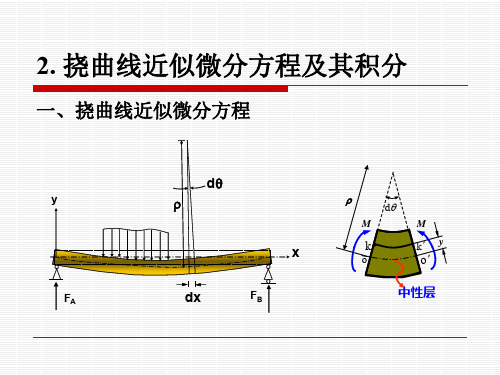
(x) 1 ( M(x)dx) cx D EI
2. 挠曲线近似微分方程及其积分
(2) 边界条件和连续条件 边界条件：梁在其支承处截面的挠度或转角是已知的，
这样的已知条件称为边界条件。
P D
固定端处 0 ， 0
P
A
C
B
铰支座处 0
M( x1 )
EI
x1
)
ql 2 8
EI ( x1 ) EI1 m( x1 )dx c1
ql 2 8
x1
c1
──── (1)
EI( x1）
EI1
M( x1)dx
dx
c1 x1
D1
ql 2 16
x12
c1 x1
D1
─ (2)
BC段： EI2
EI ( x2 )
d 2 M ( x)
dx2 EI
当y轴向上为正方向时，恒同号。
d 2
dx2
M(x) EI
——这个等式称为挠曲线近似微分方程。
2. 挠曲线近似微分方程及其积分
二、挠曲线近似微分方程的积分法
(1) 转角方程和挠度方程 对挠曲线的近似微分方程一次积分，得转角方程：
(x) d 1 ( M(x)dx c) dx EI
2. 挠曲线近似微分方程及其积分
连续条件：当弯矩方程需要分段建立时， 梁的挠曲线分段处满足的连续、光滑条件， 这样的已知条件称为连续条件。即在梁的 同一截面上应具有相同的挠度和转角。
2. 挠曲线近似微分方程及其积分
挠曲线近似微分方程
C1
Fb 6l
l2 b2
,
C2
Fab 6l
l
a
Page 14
材料力学 第六章 弯曲变形
四 积分法总结
❖ 优点：适用范围广、精确 ❖ 缺点：计算繁琐
五 刚度条件
w
max ቤተ መጻሕፍቲ ባይዱax
w
练习：写边界条件和连续性条件
A
B
C
D
边界条件 wA 0; wB 0
连续性条件 wC wC;C C 或wC' wC' wD wD;D D 或wD' wD'
Mi EI wi" M EIw" M
w
wi
Page 19
材料力学 第六章 弯曲变形
例一：求图示简支梁C点挠度
y A
l/2
F
C l/2
x B
=
y
y
F
A
C
+ x
B
A
x
C
B
l/2
l/2
l/2
l/2
wC
wC q
wC F
5ql4 384EI
Fl 3 48EI
材料力学 第六章 弯曲变形
Page 20
Page 16
材料力学 第六章 弯曲变形
练习（续）
y
a
x
b
l
边界条件 w 0; 0
x0
x0
连续性条件
w w ;
w w ;
xa
xa xa
xa
xb
xb xb
xb
Page 17
材料力学 第六章 弯曲变形
一 叠加§原理6.4 用叠加法求梁的变形
梁的位移与挠曲线近似微分方程
积分常数利用梁的边界条件及连续光滑条件来求得。
边界条件：梁横截面的已知位移条件或约束条件。
连续光滑条件：在相邻梁段的交接处即分段处， 相连两截面应具有相同的转角与挠度。
确定积分常数举例：
边界条件：
连续条件：
x0: A 0 x0: y A 0
x1 0, y A 0 x2 0, yB 0
1.基本概念:
转角
挠度 挠曲线 1、弯曲变形的表示方法：
y
（1）挠度y：截面形心在y 方向的位移;
y
x
x
挠曲线方程：
y y( x )
（2）转角θ:某横截面绕 自己的中性轴转动的角度。 转角方程：
由于小变形，截面形心在x方向的 位移忽略不计挠度转角关系为：
dy tan dx
讨
论
积分法求变形有什么优缺点？
9.7 叠加法求梁的变形
梁在若干个载荷共同作用时的挠度或转角，等 于在各个载荷单独作用时的挠度或转角的代数和。 这就是计算弯曲变形的叠加法。 即叠加法是： 分别求出各载荷单独作用时的变形，然后把各载荷在 同一处引起的变形进行叠加(代数叠加)。
直接查表： pl 3 Pl 2 y BP BP 3EI 2 EI ql 4 ql 3 y Bq Bq 8 EI 6 EI 由叠加法得：
例1 求梁的转角方程和挠度方程，并求最大 转角和最大挠度，梁的EI已知。
解: 1）由梁的整体平衡分析可得：
2）写出x截面的弯矩方程
A
)
F B
X A 0, YA F (), m A Fl (
x
l
yB
B
x
M ( x ) F (l x分方程并积分 d2y EI 2 M ( x) F (l x) dx dy 1 积分一次 EI EI F (l x) 2 C dx 2 1 再积分一次 EIy F (l x) 3 Cx D 6
材料力学 积分法求梁的变形
一、挠曲线近似微分方程
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段，共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点： A = 0, q A = 0
B 点 ： w B 左 = w B 右
C点 ： w C左 = w C右
D点：w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段，共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点： A = 0, q A = 0
B 点 ： w B 左 = w B 右
C点 ： w C左 = w C右
D点：w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
大挠度fmax和最大转角max。
解: 由对称性可知梁的两个支反力为
RA
q
RB
ql RA RB 2
A
B
x
y
l
例题 6 -2 图
此梁的弯矩方程及挠曲线微分方程分别为
ql 1 2 q M ( x) x qx (lx x 2 ) 2 2 2 q 2 EI ' ' M ( x) (lx x ) 2
EI ' ' M ( x) Pl Px (2)
例题 6-1 图
对挠曲线近似微分方程进行积分, 得
Px 2 EI ' Plx C1 (3) 2 Plx 2 Px 3 EI C1 x C 2 (4) 2 6
边界条件为 :
x
A
l x
B x
x 0, 0 x 0, ' 0
EIυ [ M ( x )dx ]dx C1x C2
得
C1 EI '| x 0 EI 0 C2 EI 0
式中，θ 0 和 v0 分别代表坐标原点处截面的转角和挠度。
例题６-３ 图示一抗弯刚度为EI的简支梁, 在D点处受一集中 力P的作用。试求此梁的挠曲线方程和转角方程，并求其最大 挠度和最大转角。
两段梁的挠曲线方程分别为
1 挠曲线方程 转角方程 挠度方程
( 0 «x «a)
2
( a«x « l )
b " P x EIv1 M1 l
b EIv2 " M 2 P x P( x a) l
3 θA ql θ max θB 24 EI
x
q
A
l 2
RB
B CθB x
A
y
l
在梁跨中点 l/2 处有 最大挠度值
fmax
5ql υ | l x 384EI 2
RA
x
4
q
A
l 2
RB
B Cθ B x
说明: 积分常数 C1 和 C2
几何意义
A
y
l
f max
将 x=0 代入
EIυ ' M( x )dx C1
l
y
f max
max 及 fmax 都发生在自由端截面处
max
f max Pl 2 Pl 2 Pl 2 |x l EI 2 EI 2 EI Pl 3 Pl 3 Pl 3 |x l 2 EI 6 EI 3EI
例题 6-1 图
例题 6-2 图示一抗弯刚度为EI的简支梁, 在全梁上受集度为q的 均布荷载作用。试求此梁的挠曲线方程和转角方程, 并确定其最
(b) A B
(a)
νA0
A
νB0
B
νA0
θA0
图 6 -4
例题 6 -1
图示一抗弯刚度为EI的悬臂梁, 试求梁的挠曲线方程
和转角方程, 并确定其最大挠度
fmax 和最大转角 max 。 解： 弯矩方程为 x
A
l x
B x
M ( x) P(l x)
(1)
y
l
挠曲线的近似微分方程为
2 3
)
2
M( x ) EI
（6 -1）
ν'
2
与 1 相比十分微小而可以忽略不计, 故上式可近似为：
M( x ) ν" EI
（6 -2 a）
此式称为 梁的挠曲线近似微分方程
近似原因 : (1) 略去了剪力的影响 ; (2) 略去了2 项。
若为等截面直梁, 其抗弯刚度EI为一常量上式可改写成
y
l
将边界条件代入(3) 可得
(4)两式中, 例题 6-1 图
C1=0
及
C2=0
将已确定的积分常数代入(3) 方程和挠曲线方程分别为
(4)两式中, 即得梁的转角
Plx Px 2 ' EI 2 EI
Plx 2 Px 3 2 EI 6 EI
x
A
l x
B x
θ max
(b)
o 在规定的坐标系中, x 轴水平向右 为正, y 轴竖直向下为正。 y 曲线向上凸 时 : > 0 , M < 0 曲线向下凸 时 ： < 0 , M > 0
M M
x
M<0
ν" 0
o
M M
x
因此, M 与 的正负号正好相反，
所以
y
M>0
ν" 0
图 6 -2
υ '' (1υ'
x 0,
x l,
v0
v0
将边界条件代入 (c) , (d) 两式得
C2 0
ql C1 24
3
梁的转角方程和挠曲线方程分别为
q ' (l 3 6lx 2 4 x3 ) 24 EI RA qx 3 2 3 (l 2lx x ) 24 EI
在 x0 和 xl 处 转角的绝对值最相等， 且都是最大值
EIυ
''
M( x )
（6 -2 b）
上式积分一次得转角方程
EIυ ' M ( x )dx C1
再积分一次, 得挠曲线方程
（6 -3 a）
EIυ [ M ( x )dx ]dx C1x C2
（6 -3 b）
式中积分常数C1 、C2可通过梁挠曲线的边界条件来确定。 在简支梁（图6 -4a）中， 左右两铰支座处的挠度 A 和 B 都应等于零。 在悬臂梁 ( 图 6 -4 b）中， 固定端处的挠度Ａ和转角 A都应等于零等等。
RA
A x q
(a) (b)
RB
B x
y
l
2 q EIυ ' ' M ( x ) (lx x ) 2
(b)
q lx 2 x3 EI ' ( ) C1 2 2 3 q lx3 x 4 EI ( ) C1 C2 2 6 12
边界条件为 :
(c) (d)
§6-2
推导公式
梁的挠曲线近似微分方程及其积分
纯弯曲时曲率与弯矩的关系为
1 M k ρ EI
横力弯曲时, M 和 都是x的函数 。略去剪力对梁的位移的影响, 则
1 M ( x) ( x) ( x) EI
由几何关系知, 平面曲线的曲率可写作
(a)
1 d | ' '| | | 3 2 ( x) ds (1 ' ) 2
RA
解: 此梁的两个支反力为
A 1
P
RB
B
D 2
b RA P l
a
l
b
a RB P l
例题 6 -3 图
RA
A
P
RB
B
1
D 2
两段梁的弯矩方程分别为
a
l
b
例题 6 -3 图
b M1 RA x P x l b M (0 x a) (a x l )