9.5 梁的位移与挠曲线近似微分方程
合集下载
梁的挠曲线近似微分方程及其积分.

f (P1P2 Pn ) f1(P1 ) f2 (P2 ) fn (Pn )
二、结构形式叠加(逐段刚化法):
A a
P q
C a
P
a
a
q
a
a
+
=
例6-4-1 按叠加原理求A点转角 和C点挠度.
解、载荷分解如图
、由梁的简单载荷变形表,
查简单载荷引起的变形。
PA
Pa 2 4 EI
f ( x) M ( x) I0 M ( x)
EI ( x) I0
EI 0
EI 0 f ( x) M ( x)
M(x) M(x) I0
I(x)
:几何形状:长度不变,惯性矩变为I0 。
:实梁对应方程: EI0 f ( x) M ( x)
虚梁对应方程:
M (x) q(x)
:令:q(x) M ( x ) 依此建立虚梁上的分布载荷。
8
2
- q a2
a2
C
a
求虚梁B点的剪力和弯矩
x
13qa 3 RA 72
QB
13qa3 72
1 2
qa2 2
a
5 72
qa3
MB
13qa3 72
a
1 2
qa2 2
a
a 3
7 72
qa4
D
B
5qa 3 72EI
7qa4 f B 72EI
C点左右位移怎样?
四、变截面直梁的共轭梁法: :将截面的变化折算到弯矩之中去。
梁的挠曲线微分:方E程 If ( x) M ( x) 梁的外载与内力的为关 : M系(x) q(x)
上二式形式相同,用类比法,将微分方程从形式上转化为 外载与内力的关系方程。从而把求挠度与转角的问题转化为求 弯矩与剪力的问题。
二、结构形式叠加(逐段刚化法):
A a
P q
C a
P
a
a
q
a
a
+
=
例6-4-1 按叠加原理求A点转角 和C点挠度.
解、载荷分解如图
、由梁的简单载荷变形表,
查简单载荷引起的变形。
PA
Pa 2 4 EI
f ( x) M ( x) I0 M ( x)
EI ( x) I0
EI 0
EI 0 f ( x) M ( x)
M(x) M(x) I0
I(x)
:几何形状:长度不变,惯性矩变为I0 。
:实梁对应方程: EI0 f ( x) M ( x)
虚梁对应方程:
M (x) q(x)
:令:q(x) M ( x ) 依此建立虚梁上的分布载荷。
8
2
- q a2
a2
C
a
求虚梁B点的剪力和弯矩
x
13qa 3 RA 72
QB
13qa3 72
1 2
qa2 2
a
5 72
qa3
MB
13qa3 72
a
1 2
qa2 2
a
a 3
7 72
qa4
D
B
5qa 3 72EI
7qa4 f B 72EI
C点左右位移怎样?
四、变截面直梁的共轭梁法: :将截面的变化折算到弯矩之中去。
梁的挠曲线微分:方E程 If ( x) M ( x) 梁的外载与内力的为关 : M系(x) q(x)
上二式形式相同,用类比法,将微分方程从形式上转化为 外载与内力的关系方程。从而把求挠度与转角的问题转化为求 弯矩与剪力的问题。
概述梁的挠曲线近似微分方程及其积分用积分

x 0 时, , wA 0 A w A 0
当
求得:
C 0; D 0
y
L
P
B
B
wB
x
写出挠曲线方程并画出挠曲线的大致形状
Px 2 w( x) ( x 3L) 6EI
最大转角及最大挠度(绝对值最大)
max
PL2 B ( ) 2 EI
wmax
PL3 wB ( ) 3EI
C
x1
x2
AB段 (0 x1 a)
a
a
M1 Px1
BC段 (0 x2 a)
M 2 P(a x2 )
写出挠曲线微分方程并积分 AB段
M1 Px1 EIw1
P 2 EI1 x1 C1 EIw1 2 P 3 EIw x1 C1 x1 D1 6
1
y
M<0
d2w 0 2 dx
d2w M ( x) 2 EI dx
o
x
d 2 w M ( x) (2) 2 EI dx
式(2)就是挠曲线近似微分方程。
对于等截面直梁,挠曲线近似微分方程可写成如下形式:
d w M ( x) 2 EI dx
二、求转角方程、挠曲线方程 1.微分方程的积分
最大挠度及最大转角
dw( x 2 ) Pa 2 ( x2 ) dx 2 2 EI
2
y
a
P
C
C
max C CB
wmax
Pa 2 2EI
L
B
x
wB
Pa 2 wB (3L a) 6EI
例2 求图示梁自由端的转角和挠度。
材料力学 梁 弯曲位移

D点的连续条件: x = a, 1' 2 ' 1 2
1 ( 0 x a)
2 (axl )
挠曲线方程
EI
1"
M1
F
b l
x
EI
2"
M
2
F
b l
x
F
(
x
a)
转角方程
EI
'
1
F b l
x2 2
C1
EI
2'
F
b l
x2 2
F
(
xa)2 2
D1
挠度方程
EI
1
F
b l
x3 6
C1 x
C2
EI
2
F
b l
式中:积分常数 C1 、C2 可通过梁挠曲线的 边界条件 和 变形 连续性条件 来确定。
1、边界条件
A
l A= 0
B
B= 0
A
A= 0
B
B= 0
在简支梁或外伸梁中, 铰支座处的挠度 都应等于零。
A 0 B 0
A
B
l A= 0 A= 0
在悬臂梁 中,固定端处的挠度 和转角 都应等于零。
A 0, A 0
F
(
xa)2 2
D1
挠度方程
EI
1
F
b l
x3 6
C1 x
C2
EI
2
F
b l
x3 6
F
(x 6
a)3
D1
x
D2
x = 0 , 1 = 0
x = l , 2= 0
再将边界条件代入方程可解得:
讲梁的挠曲线方程与积分解法
②积分常数的确定——边界条件和连续条件:
边界条件:梁在其支承处的挠度或转角是已知的, 这样的已知条件称为边界条件。 连续条件:梁的挠曲线是一条连续、光滑、平坦 的曲线。因此,在梁的同一截面上不可能有两个 不同的挠度值或转角值,这样的已知条件称为连 续条件。
边界条件
积分常数2n个=2n个
连续条件
列出图示结构的边界条件和连续条件。
8
代入(1)(2)得:
1 ( 1 qx3 1 qL3)
EI 6 6
1 ( 1 qx4 qL3 x qL4 )
EI 24
68
将 x 0 代入得:
A
qL3 6EI
(与C比较知E:I A C)
A
qL4 8EI
(与D比较知E:IA )D
因此
常数C表示起始截面的转角×刚度(EI)
常数D表示起始截面的挠度×刚度(EI)
x L
2
2、
d 2
dx 2
M (x) EI z
EI" 1 qx2
2
积分一次: EI' EI 1 qx3 C (1)
积分二次:
6
EI 1 qx4 Cx D (2)
24
B X``
3、确定常数C、D.
由边界条件: x L, 0 代入(1)得: C 1 qL3
6
x L, y 0 代入(2)得: D 1 qL4
支座反力,分段列弯矩方程; 分段的原则:
①凡载荷有突变处(包括中间支座),应作为分段点;
②凡截面有变化处,或材料有变化处,应作为分段点;
③中间铰视为两个梁段间的联系,此种联系体现为两部分之间 的相互作用力,故应作为分段点;
(2)分段列出梁的挠曲线近似微分方程,并对其积分 两次
10-1 梁挠曲线的近似微分方程

1
第十章
§10–1
目录
梁的弯曲变形
梁挠曲线的近似微分方程
§10–2 用积分求梁的变形 §10–3 叠加法求梁的变形 §10–4 梁的刚度计算和提高梁刚度的措施
2
教学内容: • 梁的挠曲线近似微分方程、转角和位移、边界 条件和连续条件的概念。 教学要求: • 1、理解梁变形的两个基本量(挠度和转角) • 2、掌握梁的挠曲线近似微分方程; • 重点:梁的挠曲线近似微分方程。 • 学时安排:1
P 2
P 2
P
7
§10–1 梁挠曲线的近似微分方程
三、弯曲变形的度量
1、梁的变形: 梁承载前后形状的变化称为变形,一般用各段梁曲率的变 化表示。 2、梁的位移: 梁变形前后位置的变化称为位移,位移包括线位移和角位移。 P y x
3、挠曲线: v=f(x)
f(x)
纵向对称面上,作用横向力,变形后,轴线由原来的 直线变成曲线,为纵向对称面内的一条光滑的曲线,称为 挠曲线 。
1 v ( x) [1 (v) 2 ]3/2
1 v ( x)
y M(x)>0
d v dx2
2
在小变形时,梁的挠曲线是 一条平缓的曲线,转角 v ' tan 的数值很小,可忽略不计。 弯矩M与挠曲线曲率 v 的值 总是异号的。 y M(x)<0
d 2v dx
2
M x v EI
x
x
0 (v 0)
0 (v 0)
M x v EI
挠曲线的近似微分方程
11
挠曲线的近似微分方程
M ( x) v EI
EIv M ( x)
由上式进行积分,就可以求出梁横截面的转角方程和挠度方程
第十章
§10–1
目录
梁的弯曲变形
梁挠曲线的近似微分方程
§10–2 用积分求梁的变形 §10–3 叠加法求梁的变形 §10–4 梁的刚度计算和提高梁刚度的措施
2
教学内容: • 梁的挠曲线近似微分方程、转角和位移、边界 条件和连续条件的概念。 教学要求: • 1、理解梁变形的两个基本量(挠度和转角) • 2、掌握梁的挠曲线近似微分方程; • 重点:梁的挠曲线近似微分方程。 • 学时安排:1
P 2
P 2
P
7
§10–1 梁挠曲线的近似微分方程
三、弯曲变形的度量
1、梁的变形: 梁承载前后形状的变化称为变形,一般用各段梁曲率的变 化表示。 2、梁的位移: 梁变形前后位置的变化称为位移,位移包括线位移和角位移。 P y x
3、挠曲线: v=f(x)
f(x)
纵向对称面上,作用横向力,变形后,轴线由原来的 直线变成曲线,为纵向对称面内的一条光滑的曲线,称为 挠曲线 。
1 v ( x) [1 (v) 2 ]3/2
1 v ( x)
y M(x)>0
d v dx2
2
在小变形时,梁的挠曲线是 一条平缓的曲线,转角 v ' tan 的数值很小,可忽略不计。 弯矩M与挠曲线曲率 v 的值 总是异号的。 y M(x)<0
d 2v dx
2
M x v EI
x
x
0 (v 0)
0 (v 0)
M x v EI
挠曲线的近似微分方程
11
挠曲线的近似微分方程
M ( x) v EI
EIv M ( x)
由上式进行积分,就可以求出梁横截面的转角方程和挠度方程
梁的弯曲-变形刚度计算

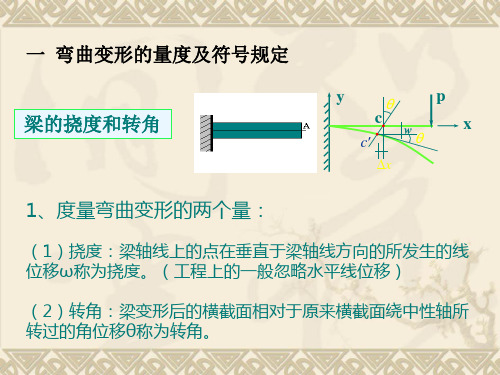
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
C'
y
1'
1
Байду номын сангаас
y f ( x)
——挠曲线方程
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
1'
y
C'
1
在小变形下: 即:
dy y tan dx
——转角方程
任一横截面的转角 = 挠曲线在该截面形心处切线的斜率
2
9 ql 2 128
M max
1 2 M A ql 8
例 14 试作图示超静定梁的剪力图和弯矩图。
q
5.讨论 设MA为多余约束力 列变形几何方程
A Aq AM 0
A
A l
B 原结构
q MA A B 静定基
查表
Aq
ql M Al , AM A 24 EI 3 EI
5Fl 3 Fl 2 Fl 3 l 6 EI 3 EI 2 EI
F A l C l
Me B
yBM
A F A C B
e
BM
B
e
Me
BF
yBF
3. Me和F共同作用时
2 M e l Fl 2 B BM e BF EI 2 EI 2 M e l 2 5Fl 3 y B y BM e y BF EI 6 EI
2.确定积分常数
FBy=
l
Me l
由 y x 0 0, D 0
工程力学第1节 挠曲线近似微分方程
挠曲轴线 近似微分方程 结论
M ( x) y EI
两种情况下弯矩与曲线的二阶导数均同号,微分 方程式应取正号,即: 挠曲轴线 近似微分方程
M ( x) y EI
梁的挠曲轴线近似微分方程的适用条件:梁的变 形是线弹性的小变形。
M ( x) y EI
微分方程弯矩M与曲线的二阶导数 y的正负号关系
1)如图a所示,梁的挠曲轴线是一下凸曲线,梁的下 侧纤维受拉,弯矩 M >0,曲线的二阶导数 y >0;
2)如图b所示,梁的挠曲轴线是一上凸曲线,梁的下 侧纤维受压,弯矩 M <0,曲线的二阶导数 y <0;
第十章
梁的弯曲变形
一、挠曲轴线近似微分方程
挠曲轴线:图示悬臂 梁在纵向对称面内的 外力 F 的作用下,将 产生平面弯曲,变形 后梁的轴线将变为一 条光滑的平面曲线, 称梁的挠曲轴线。
挠曲轴线方程
y f ( x)
y f ( x)
挠度:截面形心线位移的垂直分量称为该截面的 挠度,用 y 表示。
第ቤተ መጻሕፍቲ ባይዱ章
梁的弯曲变形
工程中的很多结构或构件在工作时, 不但要满 足强度条件,同时对于弯曲变形都有一定的要求:
第一类是要求梁的位移不得超过一定的数值。例如 若机床主轴的变形过大,将会影响齿轮的正常啮合 以及轴与轴承的正常配合,造成不均匀磨损、振动 及噪音,缩短了机床的使用寿命,还影响机床的加 工精度。因此,在工程中进行梁的设计时,除了必 须满足强度条件之外,还必须限制梁的变形,使其 不超过许用的变形值。 第二类是要求构件能产生足量的变形。例如车辆钢 板弹簧,变形大可减缓车辆所受到的冲击;跳水起 跳板大变形,以确保运动员被弹起。
转角:横截面绕中性轴转动产生了角位移,此角 位移称转角,用 表示。小变形时,转角 很小, 则有以下关系:
材料力学(土木类)第五章 梁弯曲时的位移(2)
逆时针) (逆时针)
3 3 3
利用叠加原理求图示弯曲刚度为EI的悬臂梁 例5-6 利用叠加原理求图示弯曲刚度为 的悬臂梁 自由端B截面的挠度和转角 截面的挠度和转角。 自由端 截面的挠度和转角。
F A l C EI l F D l B
原荷载可看成为图a和 两种荷载的叠加 两种荷载的叠加, 解:原荷载可看成为图 和 b两种荷载的叠加,对应 的变形和相关量如图所示。 的变形和相关量如图所示。
Fl θ C1 = 2 EI
2
3
由位移关系可得此时B截面的挠度和转角为: 由位移关系可得此时 截面的挠度和转角为: 截面的挠度和转角为
Fl 3 Fl 2 4 Fl 3 wB1 = wC1 + θ C1 ⋅ BC = + × 2l = 向下) (向下) 3EI 2 EI 3EI Fl θ B1 = θ C1 = 2 EI
q ( x) x 2 dθ B = dθ ( x) = dx 2 EI
范围对q(x)dx的作用进行叠加,相当于 的作用进行叠加, 在x=0, l范围对 范围对 的作用进行叠加 对上两式在前述范围内积分, 对上两式在前述范围内积分,即:
wB = ∫ d wB = ∫
0
l
l
0
11q 0 l q ( x ) x (3l − x ) dx = 6 EI 120 EI
上次课回顾: 上次课回顾:
1、度量梁变形的两个基本位移量:挠度和转角 度量梁变形的两个基本位移量: 2、挠曲线近似微分方程
EIw′′ = − M ( x )
3、挠曲线近似微分方程的积分 、
EIw ' ( x ) = ∫ ( − M ( x )) dx + C1
EIw ( x ) =
3 3 3
利用叠加原理求图示弯曲刚度为EI的悬臂梁 例5-6 利用叠加原理求图示弯曲刚度为 的悬臂梁 自由端B截面的挠度和转角 截面的挠度和转角。 自由端 截面的挠度和转角。
F A l C EI l F D l B
原荷载可看成为图a和 两种荷载的叠加 两种荷载的叠加, 解:原荷载可看成为图 和 b两种荷载的叠加,对应 的变形和相关量如图所示。 的变形和相关量如图所示。
Fl θ C1 = 2 EI
2
3
由位移关系可得此时B截面的挠度和转角为: 由位移关系可得此时 截面的挠度和转角为: 截面的挠度和转角为
Fl 3 Fl 2 4 Fl 3 wB1 = wC1 + θ C1 ⋅ BC = + × 2l = 向下) (向下) 3EI 2 EI 3EI Fl θ B1 = θ C1 = 2 EI
q ( x) x 2 dθ B = dθ ( x) = dx 2 EI
范围对q(x)dx的作用进行叠加,相当于 的作用进行叠加, 在x=0, l范围对 范围对 的作用进行叠加 对上两式在前述范围内积分, 对上两式在前述范围内积分,即:
wB = ∫ d wB = ∫
0
l
l
0
11q 0 l q ( x ) x (3l − x ) dx = 6 EI 120 EI
上次课回顾: 上次课回顾:
1、度量梁变形的两个基本位移量:挠度和转角 度量梁变形的两个基本位移量: 2、挠曲线近似微分方程
EIw′′ = − M ( x )
3、挠曲线近似微分方程的积分 、
EIw ' ( x ) = ∫ ( − M ( x )) dx + C1
EIw ( x ) =
梁的挠曲线近似微分方程
由边界条件:
x 0,yA 0 ; D 0
xl,
yB 0 ;
C ql3 24
q
A
x θA
θB
y
l
B
x
EIy ql x3 q x4 Cx D 12 24
EIy ql x2 q x3 ql3 4 6 24
q (l3 6lx2 4x3)
ql x3 q x4 ql3 x 12 24 24
24EI
最大转角和最大挠度分别为:
y qx (l3 2lx2 x3) 24EI
ymax
y
x l 2
5ql 4 384EI
max
A
B
ql3 24 EI
外伸梁,承受集中载荷作用,试绘制挠曲线的大致形状图。 设弯矩刚度EI为常数。
§6-3 用积分法求梁的变形
解:1、绘制挠曲线的基本依据
1 y M (x)
(x)
EI z
根据弯矩的正、负、零值点或零值区,确定挠曲线的凹、
凸、拐点或直线区。
在梁的被约束处,应满足位移边界条件;在分段处,则 应满足位移连续条件。
载荷作用。试求此梁的转角方程和挠度方程,并确定最大转角
和最大挠度。
y
q
解:
FRA
FRB
ql 2
A
B
x
M(x) ql x q x2 22
x
l
EIy ql x q x2 22
EIy ql x2 q x3 C 46
EIy ql x3 q x4 Cx D 12 24
§6-3 用积分法求梁的变形
§6-3 用积分法求梁的变形
梁的挠曲线近似微分方程:
d 2 y M (x) dx2 EI
梁位移
EI z
2
y(x) 1 (1 Plx2 1 Plx3)
EI z 2
6
ymax
y(l)
1 EIz
(1 2
Pl3
1 6
Pl3)
Pl3 3EIz
()
max
(l)
1 EIz
(Pl2
1 2
Pl2)
Pl2(逆时针) 2EIz
9
例2:求此梁的转角方程和挠度方程,确定最大转角,挠度。
由于梁变形后横截面仍垂直于轴线,因此任一截面的转角,
也可用截面形心处挠曲线的切线与x轴的夹角来表示。
则有: (切线) dy(x) tg
dx
因很小,可写成 tg
(x) dy(x) y
dx
即:任一横截面的转角 等于该截面处挠度y 对x的一阶导数,只
要知道梁的挠曲线方程,则可确定任一点的挠度和截面的转角。
分布力等时, 应该分段积分。每一个分段中都有两个积分常数,
它们要满足连续变形条件。
7
例1:9.1 求挠度方程和转角方程,并确定最大值。
解:确定支座反力:
RA P MA Pl
弯矩方程:
M (x) Pl Px
挠度、转角方程:
EIz (x) (Pl Px)dx C
因分段(x=a)处曲线连续变形,
y11
(a) (a)
y2
2
(a) (a)
C1
C2
Pb 6l
(b2
l2)
y1
y2 (x)
(x)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4)由位移边界条件确定积分常数
x 0, x 0,
代入求解
A 0 yA 0
1 2 1 3 C Fl , D Fl 2 6 5)确定转角方程和挠度方程 1 1 2 2 EI F (l x) Fl 2 2 1 1 2 1 3 3 EIy F (l x) Fl x Fl 6 2 6 6)确定最大转角和最大挠度 Fl 2 Fl 3 x l , max B , ymax y B 2 EI 3 EI
x1 a, x 2 b c左 c右 yc左 yc右
确定积分常数举例:
边界条件:
x 0 : y A x l : yB
连续条件: x l / 2时 : 0 C 左 C右 0 y C左 y C右
x 0 : y A 0 qla x l : y B 2 EA
4 EI z
解: 1)外力分析:
M0 M0 RA (), R B ( ) L L
2)内力分析:(M方程) 3)挠曲线方程和转角方程:
d2 y M0 EIz 2 x L dx
M0 M(x) x 0 x L L
M0 2 EIz θ x C 2L M0 3 EIz y x Cx D 6L
yC 1
3)将结果叠加
yB 2
yC 2
yC
y
i 1
2 i 1
2
Ci
41ql 4 384 EI
7 ql 3 48 EI
C
Ci
讨
论
叠加法求变形有什么优缺点?
9.8 梁的刚度条件及提高梁刚度的措施
1.刚度条件
y max [ y ],
max
[ ]
例、 已知EIZ,M0,L,求θ A,θ B,及中点的挠 ML2 度; 若 y ,试校核刚度。
[ y]
刚度满足要求。
2.提高梁刚度的措施:
1)选择合理的截面形状增大截面惯性矩
2)改善结构形式,减小弯矩数值
3)采用超静定结构
小
结
基本要求: 掌握弯曲的概念和实例,梁的计算简图,掌握纯弯曲的正应力 公式,弯矩与挠曲线曲率间的关系,抗弯刚度,抗弯截面模量, 纯弯曲理论的推广,熟练掌握梁按正应力的强度计算。 掌握矩形截面梁的剪应力,工字形截面梁的剪应力,梁按剪应 力的强度校核,提高弯曲强度的措施。 掌握梁的变形和位移,挠度和转角,梁的挠曲线及其近似微分 方程,用积分法求梁的挠度转角,根据叠加法求梁的挠度转角, 梁的刚度校核,提高梁的刚度措施。 重点: 梁按正应力的强度计算,梁按剪应力的强度校核。 难点: 梁的刚度校核。
dy tan dx
y (x)
表明:挠曲线上某点切线的斜率等于该点横截面的转角。
2.挠曲线的近似微分方程:
推导弯曲正应力时,得到:
1 M ρ EI z
忽略剪力对变形的影响
1 M ( x) ( x) EI z
由数学知识可知:
d2y 1 dx 2 dy 2 3 [1 ( ) ] dx
例1 求梁的转角方程和挠度方程,并求最大 转角和最大挠度,梁的EI已知。
解: 1)由梁的整体平衡分析可得:
2)写出x截面的弯矩方程
A
)
F B
X A 0, YA F (), m A Fl (
x
l
yB
B
x
M ( x ) F (l x ) F ( x l )
y
3)列挠曲线近似微分方程并积分 d2y EI 2 M ( x) F (l x) dx dy 1 积分一次 EI EI F (l x) 2 C dx 2 1 再积分一次 EIy F (l x) 3 Cx D 6
为了利用梁全长承受均 布载荷的已知结果,先将均 布载荷延长至梁的全长,为 了不改变原来载荷作用的效 果,在AB 段还需再加上集 度相同、方向相反的均布载 荷。
yC
2)再将处理后的梁分解为简单 载荷作用的情形,计算各自C截 面的挠度和转角。
ql 4 ql 3 y C1 , C1 8EI 6 EI l yC 2 y B 2 B 2 2 ql 4 ql 3 l , 128EI 48 EI 2 ql 3 C2 48EI
2
9.6 积分法求弯曲变形
挠曲线的近似微分方程为:
d y M ( x) EI z dx 2
2
d2y EI z 2 M ( x) dx
积分一次得转角方程为:
dy EI z EI z M ( x)dx C dx
再积分一次得挠度方程为:
EI z y M ( x)dxdx C x D
4)确定积分常数:
x 0, y0 yA 0
x L, yL yB 0
得:
D0
M0 2 M0L 所以 EIz θ x 2L 6 M0 3 M0L EIz y x x 6L 6
M0L C 6
5)求θ A,θ B。
M0L ( A 0 6 EI Z M0L B L ( 3EI Z
9.5 梁的位移与挠曲线近似微分方程
1.基本概念:
转角
挠度 挠曲线 1、弯曲变形的表示方法:
y
(1)挠度y:截面形心在y 方向的位移;
x
y
x
挠曲线方程:
y y( x )
(2)转角θ:某横截面绕 自己的中性轴转动的角度。 转角方程:
由于小变形,截面形心在x方向的 位移忽略不计挠度转角关系为:
)
)
中点的挠度: M0 1 3 M0L 1 L EIz y ( ) ( L) ( L) 2 6 2 6 2
M 0 L2 L y( ) () 2 16 EIz
6)刚度校核:
y' 0(即θ 0处) L x 3
M0 2 M0L x 0 2L 6
y max
M0L
2
9 3EI Z
讨
论
积分法求变形有什么优缺点?
9.7 叠加法求梁的变形
梁在若干个载荷共同作用时的挠度或转角,等 于在各个载荷单独作用时的挠度或转角的代数和。 这就是计算弯曲变形的叠加法。 即叠加法是: 分别求出各载荷单独作用时的变形,然后把各载荷在 同一处引起的变形进行叠加(代数叠加)。
直接查表: pl 3 Pl 2 y BP BP 3EI 2 EI ql 4 ql 3 y Bq Bq 8 EI 6 EI 由叠加法得:
略去高阶小量,得
d2y 2 dx 1
所以
d 2 y M ( x) 2 dx EI z
由弯矩的正负号规定可得,当y坐标向下时,弯 矩的符号与挠曲线的二阶导数异号,所以挠曲线的 近似微分方程为:d y M ( x) 2 EI Nhomakorabeaz dx
EIZ——抗弯刚度 由上式进行积分,就可以求出梁横截面的转角 和挠度。
积分常数利用梁的边界条件及连续光滑条件来求得。
边界条件:梁横截面的已知位移条件或约束条件。
连续光滑条件:在相邻梁段的交接处即分段处, 相连两截面应具有相同的转角与挠度。
确定积分常数举例:
边界条件:
连续条件:
x0: A 0 x0: y A 0
x1 0, y A 0 x2 0, yB 0
y B y BP Pl 3 ql 4 y Bq 3EI 8EI
B BP Bq
pl 2 ql 3 2 EI 6 EI
yC
例 已知:悬臂梁受力如 图示,q、l、EI均为已知。 求C截面的挠度yC和转角C
解: 1)首先,将梁上的载荷变成 有表可查的情形
