整数乘分数的意义和计算
分数乘法知识点总结

分数乘法单元总结一、分数乘法(一)1、分数乘整数的意义:是求几个同样加数(这里的加数是指分数)的和的简易运算。
2、分数乘整数的计算方法:分数和整数相乘,用分数的分子和整数相乘的积作分子,分母不变。
二、分数乘法(二)1、分数乘整数的意义 :整数乘分数的意义能够依据分数的意义来推测,也能够把这个整数看作单位“ 1”,均匀分红几份,再取此中的几份,也就是求这个数的几分之几。
2、求一个数的几分之几是多少的计算方法 :由分数的意义看出,求一个数的几分之几是多少,就是把前方这个数看坐单位“ 1”,求这个整体的几分之几是多少,依据整数乘分数的意义要用乘法计算。
也就是用这个数乘后边的几分之几,即乘这个分数 .3、已知一个数多几分之几求多多少?已知比一个数多几分之几,求多多少,用乘法计算三、分数乘法(三)1、分数乘分数的意义:是求一个数的几分之几是多少。
2、分数乘分数的计算方法:分子相乘,乘得的积作分子,分母与分母相乘的积作分母。
在计算时能约分的先约分。
最后结果要化成最简分数。
3、一个数与分数相乘,积与这个数的关系:一个数乘真分数,积小于这个数;一个数乘假分数,积等于或大于这个数。
(假如所乘额分数大于 1,积是大于这个数。
假如所乘的分数小于 1,积小于这个数。
)四、倒数1、倒数的意义:假如两个数的乘积是 1,那么我们称此中一个数是另一个数的倒数。
倒数是对两个数来说的,它们是相互依存的,一定说一个数另一个数的倒数,不可以孤立的某一个数是倒数。
2、求一个数的倒数的方法:( 1)由于互为倒数的两个数的分子、分母是调动地点的,依据这点,我们能够求一个数的倒数。
给出一个数,只需我们将其化为分数的形式再调动它的分子、分母的地点,就求出了它的倒数。
关于一个自然数( 0 除外),我们能够把它当作分母是 1 的分数,再调动分子和分母的地点,求出这个数的倒数。
( 2)1 的倒数是 1,由于 1 乘 1 得 1,切合倒数的意义。
( 3)0 没有倒数。
知识点总结分数乘法

六年级上册数学第一单元分数乘法知识点总结(一)分数乘法的意义。
1 、分数乘整数(第二个因数为整数时):分数乘整数的意义与整数乘法的意义相同,都是求几个相同加数和得简易运算。
2 2 2比如:3 ×3,表示: 3 个3 相加是多少,还表示 3 的 3 倍是多少。
2 、一个数(小数、分数、整数)乘分数(第二因数为真分数时):一个数乘分数的意义与整数乘法的意义不相同,是表示这个数的几分之几是多少。
5 5比如: 6×12 ,表示:6 的12 是多少。
2 7 2 77 ×8 ,表示:7 的8 是多少。
3、一个数(小数、分数、整数)乘分数(第二因数为大于1 的分数时):一个数乘分数的意义与整数乘法的意义也不相同,是表示这个数的几倍是多少。
5 2 5 2比如:12×13 ,表示:12 的 13 倍是多少。
(二)、分数乘法的计算法例:1、分数乘整数的运算法例是:分子与整数相乘,分母不变。
注:(1)为了计算简易能约分的可先约分再计算。
(分母和整数约分)(2)约分是用整数和下边的分母约掉最大公因数。
(计算结果一定是最简分数)2、分数乘分数的运算法例是:用分子相乘的积做分子,分母相乘的积做分母。
(分子乘分子,分母乘分母)注:(1)假如分数乘法算式中含有带分数,要先把带分数化成假分数再计算。
( 2)分数化简的方法是:分子、分母同时除以它们的最大公因数。
(3)在乘的过程中约分,是把分子、分母中,两个能够约分的数先划去,再分别在它们的上、下方写出约分后的数。
(约分后分子和分母一定不再含有公因数,这样计算后的结果才是最简单分数)(4)分数的基天性质:分子、分母同时乘或许除以一个相同的数( 0 除外),分数的大小不变。
(三)积与因数的关系:一个数(0 除外)乘大于 1 的数,积大于这个数。
a×b=c, 当 b >1 时, c>a.一个数(0 除外)乘小于 1 的数,积小于这个数。
知识点总结:分数乘法

分数乘法知识点总结(一)分数乘法的意义。
1、分数乘整数(第二个因数为整数时):分数乘整数的意义与整数乘法的意义相同,都是求几个相同加数和的简便运算。
例如:23 ×3,表示:3个 23 相加是多少,还表示 23的3倍是多少。
2、一个数(小数、分数、整数)乘分数的意义与整数乘法的意义不相同,是表示这个数的几分之几是多少。
例如:6×512 ,表示:6的512 是多少。
27 ×78 ,表示:27 的78是多少。
例如:512 ×123 ,表示:512 的123倍是多少。
(二)、分数乘法的计算法则:1、分数乘整数的运算法则是:用分子乘整数的积作分子,分母不变。
注:(1)为了计算简便能约分的可先约分再计算。
(分母和整数约分)(2)约分是用整数和下面的分母约掉最大公因数。
(计算结果必须是最简分数)2、分数乘分数的运算法则是:用分子相乘的积做分子,分母相乘的积做分母。
(分子乘分子,分母乘分母)注:(1)如果分数乘法算式中含有带分数,要先把带分数化成假分数再计算。
(2)分数化简的方法是:分子、分母同时除以它们的最大公因数。
(3)在乘的过程中约分,是把分子、分母中,两个可以约分的数先划去,再分别在它们的上、下方写出约分后的数。
(约分后分子和分母必须不再含有公因数,这样计算后的结果才是最简单分数)(4)分数的基本性质:分子、分母同时乘或者除以一个相同的数(0除外),分数的大小不变。
3.小数乘分数的计算方法(1)把小数化成分数计算;(2)如果分数能化成有限小数,也可以将分数化为小数计算;(3)小数跟分母能约分的,先约分再计算比较简便(三)积与因数的关系:一个数(0除外)乘大于1的数,积大于这个数。
a ×b=c,当b >1时,c>a.一个数(0除外)乘小于1的数,积小于这个数。
a ×b=c,当b <1时,c<a (b ≠0). 一个数(0除外)乘等于1的数,积等于这个数。
分数乘整数和整数乘分数的意义教案

分数乘整数和整数乘分数的意义教案课题:分数乘整数和整数乘分数的意义教学目标:1. 让学生理解分数乘整数和整数乘分数的意义,能正确区分两者的不同。
2. 通过实际操作和举例,培养学生的数学思维和解决问题的能力。
3. 激发学生对数学学习的兴趣,感受数学在生活中的广泛应用。
教学重点&难点:重点:掌握分数乘整数和整数乘分数的意义。
难点:能准确区分分数乘整数和整数乘分数在意义上的差异,并能正确运用。
教学方法:讲授法、演示法、讨论法、练习法相结合。
教材分析:课本原文内容:分数乘整数,例如$\frac{2}{5}×3$,表示3个$\frac{2}{5}$相加的和是多少。
整数乘分数,比如$3×\frac{2}{5}$,表示3的$\frac{2}{5}$是多少。
这部分内容是在学生掌握了分数的基本概念和整数乘法意义的基础上进行教学的,为后续学习分数乘法的计算和应用打下基础。
教学过程:1. 导入教师:同学们,咱们之前学过整数乘法,谁能说一说整数乘法的意义呀?(请几位同学回答)教师:对了,整数乘法表示几个相同加数的和的简便运算。
那今天咱们要来学习一种新的乘法,就是分数和整数相乘,这里面可藏着不少有趣的小秘密呢,大家想不想知道?2. 讲解分数乘整数的意义教师:咱们来看一个例子哈。
假如一个蛋糕平均分成5份,每份就是这个蛋糕的$\frac{1}{5}$。
小明吃了2份,那他吃了这个蛋糕的几分之几呀?(引导学生回答$\frac{2}{5}$)那要是有3个小明都吃这么多,也就是3个$\frac{2}{5}$,用乘法算式怎么表示呢?(学生回答后,教师板书:$\frac{2}{5}×3$)教师:那这个算式表示什么意义呢?其实呀,它就表示3个$\frac{2}{5}$相加的和是多少,就像整数乘法表示几个相同加数的和一样。
咱们可以写成加法算式来验证一下:$\frac{2}{5}+\frac{2}{5}+\frac{2}{5}=\frac{2 + 2 + 2}{5}=\frac{6}{5}$,和乘法算出来的结果是一样的。
分数乘整数的意义和整数乘法的意义相同

5 3
示求 4 个5 的和;也可以求 5 的 4 倍。7 × 6 表示 (
3
3
6
) 9 × 11 表示(
8
)
分数乘整数的计算法则:用分数的分子与整数相乘的积作分子,分母不变。计算过程中整数 只能和分母约分。如 × 15 = 12.
3
3
4
4 5
3 5
3 5
型:桃树的棵树比梨树多3 × 1—
1 8
1
:梨树× 1 + 3 =桃树的棵树
1
小明的身高比小敏矮8
1
小敏
= 小明的身高
5 2 3 5 3 2
简便运算定律:加法、减法; (交换律结合律) :a+b=b+a 如8 + 3 + 8 = 8 + 8 + 3
3 5
— + = + —
6 5 5 5
4 5
1 、 :○ “是”字型的关键句的单位“1”在的几分之几
的前面。如苹果的重量是梨的 ,梨的重量就是单位“1” ;红花的朵数相当于白花的 ,白花
5
3
的朵数是单位“1” 。
1 3
2 、 ○ “比”字型的关键句:单位“1”在“比”字的后面。如桃树的
棵树比梨树多 ,梨树是单位“1” ;小明的身高比小敏矮 ,小敏的身高是单位“1” 。
8
1 苹果的重量是梨的 (梨× =苹果的重量) 如何写分数关键句的关系式: “是”字型的:○ ;
1
4 5
4 5
红花的朵数相当于白花的5, (白花× 5 = 红花的朵数);苹果的重量比梨的5多 20 千克(梨
2021年北师大版数学五下第三单元《分数乘法》章节知识点、达标训练附解析
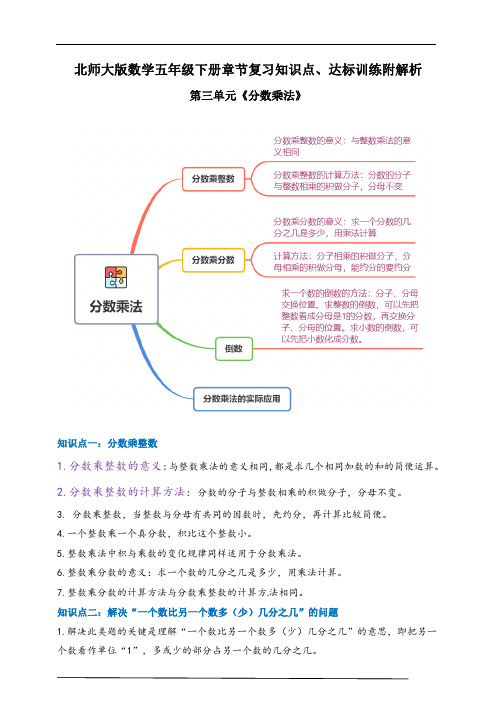
北师大版数学五年级下册章节复习知识点、达标训练附解析第三单元《分数乘法》知识点一:分数乘整数1.分数乘整数的意义:与整数乘法的意义相同,都是求几个相同加数的和的简便运算。
2.分数乘整数的计算方法:分数的分子与整数相乘的积做分子,分母不变。
3. 分数乘整数,当整数与分母有共同的因数时,先约分,再计算比较简便。
4.一个整数乘一个真分数,积比这个整数小。
5.整数乘法中积与乘数的变化规律同样适用于分数乘法。
6.整数乘分数的意义:求一个数的几分之几是多少,用乘法计算。
7.整数乘分数的计算方法与分数乘整数的计算方法相同。
知识点二:解决“一个数比另一个数多(少)几分之几”的问题1.解决此类题的关键是理解“一个数比另一个数多(少)几分之几”的意思,即把另一个数看作单位“1”,多或少的部分占另一个数的几分之几。
2. 在解决多个单位“1”的实际问题时,首先要清楚每个分数分别对应的单位“1”的量,找准数量关系后再列式解答。
3. 打几折就是按原价的十分之几销售,即几折就是原价的十分之几。
已知原价和打几折,求现价,就是求原价的十分之几是多少,用乘法计算。
知识点三:分数乘以分数1.分数乘分数的意义:求一个分数的几分之几是多少,用乘法计算。
2.分数乘分数的计算方法:分子相乘的积做分子,分母相乘的积做分母,能约分的要约分。
3. 一个数(不为0)乘一个小于1的分数,积就小于这个数;乘等于1的分数,积就等于这个数;乘大于1的分数,积就大于这个数。
知识点四:倒数1.倒数是相对于两个数来说的,它们互相依存,可以说一个数是另一个数的倒数,不能孤立地说某一个数是倒数。
2.乘积为1的两个数互为倒数。
3.求一个数的倒数的方法:分子、分母交换位置。
求整数的倒数,可以先把整数看成分母是1的分数,再交换分子、分母的位置。
求小数的倒数,可以先把小数化成分数。
4. 1的倒数是它本身,0没有倒数。
一、精挑细选(共5题;每题2分,共10分)1. 两个相同的分数相乘,积是,这个分数是()。
分数乘法知识点总结

分数乘法知识点总结分数乘法知识点总结上学期间,是不是经常追着老师要知识点?知识点是传递信息的基本单位,知识点对提高学习导航具有重要的作用。
相信很多人都在为知识点发愁,下面是小编为大家收集的分数乘法知识点总结,供大家参考借鉴,希望可以帮助到有需要的朋友。
一、分数乘法(一)分数乘法的意义1、分数乘整数与整数乘法的意义相同。
都是求几个相同加数的和的简便运算。
例如:65×5表示求5个65的和是多少?1/3×5表示求5个1/3的和是多少?2、一个数乘分数的意义是求一个数的几分之几是多少。
例如:1/3×4/7表示求1/3的4/7是多少。
4×3/8表示求4的3/8是多少?(二)、分数乘法的计算法则1、分数与整数相乘:分子与整数相乘的积做分子,分母不变。
(整数和分母约分)2、分数与分数相乘:用分子相乘的积做分子,分母相乘的积做分母。
注意:当带分数进行乘法计算时,要先把带分数化成假分数再进行计算。
3、为了计算简便,能约分的要先约分,再计算。
(尽量约分,不会约分的就不约,常考的质因数有11×11=121;13×13=169;17×17=289;19×19=361)4、小数乘分数,可以先把小数化为分数,也可以把分数化成小数再计算(建议把小数化分数再计算)。
一个数(0除外)乘大于1的数,积大于这个数。
一个数(0除外)乘小于1的数(0除外),积小于这个数。
一个数(0除外)乘1,积等于这个数。
(四)、分数混合运算的运算顺序和整数的运算顺序相同。
整数乘法的交换律、结合律和分配律,对于分数乘法也同样适用。
乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律:(a+b)×c=a*c+b*c二、分数乘法的解决问题(已知单位“1”的量(用乘法),即求单位“1”的几分之几是多少)1、画线段图:(1)两个量的关系:画两条线段图,先画单位一的量,注意两条线段的左边要对齐。
六年级数学上分数乘整数的意义和计算

1分数乘法1.本单元的内容主要包括:分数乘法、分数乘法的简便运算和解决问题三部分。
这些内容都是分数中的基础知识,不仅可以用来解决有关分数的生活实际问题,而且也是学习分数除法和百分数等知识的重要基础。
2.本单元是在学生学习了整数乘法、分数、小数的意义和性质的基础上进行教学的。
因此不再单独教学分数乘法的意义,而是通过解决实际问题,结合分数与整数、分数、小数相乘的计算过程去理解分数乘法的意义。
同时也不再呈现分数乘法的计算法则,简化了算理推导过程的叙述及解决问题思路的提示,通过直观操作、合作交流等手段,探索计算法则,寻找解题思路,自主构建新知识。
1.理解分数乘法的意义,掌握分数乘法的计算方法。
2.能进行分数乘加、乘减混合运算,能运用整数乘法运算定律进行分数乘法的简便计算。
3.会解答求一个数的几分之几是多少的实际问题,能在现实情境中体会分数乘法的实际意义。
(1)分数乘整数的意义和计算 1课时(2)整数乘分数的意义和计算 1课时(3)分数乘分数 1课时(4)分数乘法的计算方法 1课时(5)练习课 1课时(6)分数乘小数 1课时(7)分数乘法的混合运算和简便运算 1课时(8)解决问题(1) 1课时(9)解决问题(2) 1课时(10)练习课 1课时(11)整理和复习 1课时(12)重点单元知识归纳与易错警示 1课时本单元的教学中教师注意培养学生观察比较、分析归纳、动手操作能力;引导学生探究知识间的内在联系,激发学生学习兴趣;在理解算理的同时体会教学知识的魅力,领略数学的美。
第1课时分数乘整数的意义和计算(3)列出算式:92+92+92或的意义和计算。
