现代控制理论(第二章)
合集下载
现代控制理论基础_周军_第二章状态空间分析法资料
zn an1zn1 a1z a0z u
y n1zn1 1z 0z
(2-17)
定义如下一组状态变量
x1 z，x2 z， ，x0 zn1
(2-18)
可得状态方程
x1 x2
x2 x3
xn a0z a1z
它便于在模拟计算机上进行仿真，是向量-矩阵形式状态方 程的展开图形，揭示了系统的详细的内部结构。
状态变量图中仅含积分器、加法器、比例器三种元件及一 些连接线。积分器的输出均为状态变量。输出量可根据输出方 程在状态变量图中形成和引出。
例2-1的状态变量图见图2-3，图中s 为拉普拉斯算子。
图2-3 状态变量图
x2
x3
a2
y
2u
yn2
an1 yn3
un3
n2
an2
yn4
n2un4
a2 y 2u
x1 x2 a1 y 1u yn1 an1yn2 n1un2 an2 yn3 n2un3 a1 y 1u
考虑式(2-11)可得
x1 a0 y 0u a0xn 0u
故有状态方程：
x1 a0xn 0u
线性定常连续系统的动态方程的形式： ➢ 一般形式
x Ax Bu，y Cx Du
➢ 典型形式
一 物理系统动态方程的建立
实际物理系统动态方程的建立的原则： ➢根据所含元件遵循的物理、化学定律，列写其微分方程； ➢选择可以量测的物理量作为状态变量。
例2-1 设机械位移系统如图2-1 所示。力F及阻尼器汽缸速度v 为两种外作用，给定输出量为 质量块的位移x及其速度 x、加
1
b 2
n1
x1
x2
x x3
xn
c 0
浙大控制考研-现代控制理论(浙大)第二章
1 A2t 2 2!
1 k
Aktk
)
b0
t 0 x(0) b0
x(t) (I At 1 A2t 2 1 Akt k )x(0)
2!
k
eAt I At 1 A2t 2 1 Akt k
2!
k
矩阵指数函数
Φ(t) 状态转移矩阵
x(t) eAtx(0) 描述了状态向量由初始状态x(0)向任意时 刻状态 x(t)转移的内在特性。
eAt I At 1 A2t 2 1 Akt k
2!
k
1）根据状态转移矩阵的定义求解：
eAt I At 1 A2t 2 1 Akt k
2!
k!
对所有有限的t值来说，这个无穷级数都是收敛的 。
求出的解不是解析形式，适合于计算机求解。
例：求解系统状态方程 解：
x1
x2
0 0
-11
6
-6 -11 5
试计算状态转移矩阵 eAt .
解: 1) 特征值
1 1
I A 6 -11 6 1 2 3 0
6 11 5
1 1,2 2,3 3
2) 计算特征向量：
1 1 1 p1 0, p2 2, p3 6
1 4 9
3) 构造变换阵P：
1 1 1 P 0 2 6
(A B)3 A3 B3 3A2B 3AB 2
(9) x Px Φ(t) P-1Φ(t)P P-1eAtP
证明：非奇异线性变换
x Px
n n非奇异矩阵 另一组状态变量
x Px
x P1AP x x(t) eP1AP x(0)
x Ax APx 新的系统矩阵 新的状态转移矩阵
Ax
eAt x(0) Φ(t)x(0)
现代控制理论(第二章)
(1)
若初始时刻 时的状态给定为
则式(1)有唯一确定解：
若初始时刻从
开始，即
(2) 则其解为：
证明： 级数形式
和标量微分方程求解类似，先假设式(1)的解
(3) 为 的矢量幂
(4) 代入式(1)得：
(5)
既然式(4)是式(1)的解，则式(5)对任意时刻 都成立，故 的同次 幂项的系数应相等，有：
在式(4)中，令
e t e 2 t e t 2 e 2 t
x ( t ) L 1 ( s I A ) 1 x ( 0 ) L 1 ( s I A ) 1 B ( s ) U
s3
1
sIA1bU(s)(s1)(s2)
2
(s1)s(s2)1 01s
(s1)(s2) (s1)(s2)
eAtPeAtP1Pe0 1t
e0 2tP111
1et 20
02 1 e2t1 1
et e2t 2 1 2et e2t
et e2t
et 2e2t1 12et 2e2t et 2e2t
3）用拉氏变换法求解 e A tL 1 (s I A ) 1
s3
sIA1 2s
11 s3
(s
1)(s 2
或
（1）
即
2.5.2 Z 变换法
（2）
对于线性定常离散系统的状态方程，也可以来用 Z 变换法来求解。
设定常离散系统的状态方程是：
对上式两端进行 Z 变换，有： 或
线性时变系统的非齐次状态方程为：
且
的元素在时间区间
（17） 内分段连续，则其解为：
（18）
证明 线性系统满足叠加原理，故可将式(17)的解看成由初始状态
《现代控制理论》第三版 第二章.习题答案
2－7. 证明 2－3 中，状态方程的解： 1. 即当u(t ) K (t )，x(0 ) x0时
x(t ) e At x0 e At BK , 式中K 与u(t )同维的常数矢量。
x e x0 e A( t ) BK ( )d
At 0 t
e x0 e A( t ) ( )d BK
得 1 0; 2 1.
1 0 据 1 I A P P 1 1 0 1 0
得到 P 1 0 1 ；
T
0 0 P2 0 得 到 根 据 2 I A P2 1 1
1 0 1 1 1 于是T ， P2 ， T 1 1 1 1 于是 T 1 0 e 1 G (T ) e AT T T T T e 1 0 e t T T e 0 K At H (T ) e dtB dt 0 0 1 et 1 0 1 0
1
e At 0 (t ) I 1 (t ) A
1 2cos 2t 2 4sin 2t
sin 2t 2cos 2t
1 1 （2） A 4 1
1 22 1 33 A t A t 2! 3! 直接法： 7 3 t 2 13 3 2 1 5 , t t t t t 2! 6 6 2 28 3 t 13 3 2 4 4 , 1 5 t t t t t 6 2! 6 e At I At
y 2 x1 x2
1 1 0 x1 K x x 2 1 0 x2 0 即 x1 y 2 1 x2 0 u1 u 1 2
现代控制理论 2-0
∫
t
0
e − Aτ f (τ )dτ =
e [ x(0) + ∫ e
At 0 At
t
− Aτ
f (τ )dτ ] + ∫ e A( t −τ ) Bu (τ )dτ
t1 − Aτ
当t = t1时，有 x(t1 ) = e [ x(0) + ∫ e
0
f (τ )dτ ] + ∫ e A( t −τ ) Bu (τ )dτ
λ − 1 0 det[λI − A] = det = (λ − 1)(λ + 3) = 0 λ + 3 2 λ1 = 1, λ2 = −3 0 0 rank [λ1 I − AMb] = rank 2 4 − 4 rank [λ2 I − AMb] = rank 0 系统能控。 1 =2 1 0 1 =2 0 1
0
t1
∫
t1
0
e − Aτ f (τ )dτ为一个确定的值，仅仅相当于把系统
原来的初态改变了一确定的常值。所以在讨论系统 的能控性时，不考虑系统存在的确定性干扰。
第二章 系统的可观性和可控性
(三)能控性判据
判据一： 判据一：若系统能控，则能控性矩阵
Qc = [B AB A 2 B ... A n −1 B ] 满秩，即
第二章 系统的可观性和可控性
现代控制理论基础
主讲人: 主讲人:荣军 mail:rj1219 163. 1219@ E-mail:rj1219@
第二章 系统的可观性和可控性
2-1 能能控性及其判据
－、线性定常系统的能观测性及其判据 －、线性定常系统的能观测性及其判据
线性定常系统状态方程为 x = Ax + Bu 其中x、u分别为n、 r维向量，A、B为满足矩阵运算的常值矩阵。若给定系统的 一个初始状态x0和任一状态x1,如果在的有限时刻tf>0,定义在 时间区间[0，tf]的输入u（t）使状态x(0)＝x0转移到x(tf)＝ x1 ，则称系统状态完全是能控的； 如果系统对任意一个初始状态都能控，则称系统是状态完全 能控的，简称系统是状态能控的或系统是能控的。
现代控制理论第二章
（2）在e At 定义中，用（1 ）的方法可以消去 A的n及n以上的幂次项，即 e At = I + At + 1 2 2 1 1 A t +⋯+ An −1t n −1 + An t n + ⋯ 2! ( n − 1)! n!
= α n −1 (t ) An −1 + α n − 2 (t ) An − 2 + ⋯ + α1 (t ) A + α 0 (t ) I
【例2-5】见板书
（3）α i (t )的计算公式 A的特征值互异时 α 0 (t ) 1 λ1 α1 (t ) 1 λ2 ⋮ = ⋮ ⋮ α (t ) 1 λ n −1 n
λ λ λ
பைடு நூலகம்
2 1 2 2
⋮
2 n
⋯ λ e λ1t λ2 t ⋯ λ e ⋮ ⋮ λn t n −1 ⋯ λn e
At
2.变换A为约旦标准型 （1）A特征根互异 Λ = T −1 AT 有
例2-2 ，同例2-1
e At = Te ΛtT −1
（2）A特征值有重根
J = T AT e At = Te JtT −1
0 1 0 [例2 - 3]已知A = 0 0 1 , 求e At 2 - 5 4
若
σ ω A= −ω σ
则
cos ωt sin ωt σt e = Φ(t ) = e − sin ωt cos ωt
At
2.2.4 计算
1.根据 e At 或 Φ (t ) 的定义直接计算
1 2 2 1 33 1 n n e = I + At + A t + A t ⋯ A t + ⋯ 2! 3! k! 1 0 [例2 - 1]已知A = , 求e At − 2 − 3
= α n −1 (t ) An −1 + α n − 2 (t ) An − 2 + ⋯ + α1 (t ) A + α 0 (t ) I
【例2-5】见板书
（3）α i (t )的计算公式 A的特征值互异时 α 0 (t ) 1 λ1 α1 (t ) 1 λ2 ⋮ = ⋮ ⋮ α (t ) 1 λ n −1 n
λ λ λ
பைடு நூலகம்
2 1 2 2
⋮
2 n
⋯ λ e λ1t λ2 t ⋯ λ e ⋮ ⋮ λn t n −1 ⋯ λn e
At
2.变换A为约旦标准型 （1）A特征根互异 Λ = T −1 AT 有
例2-2 ，同例2-1
e At = Te ΛtT −1
（2）A特征值有重根
J = T AT e At = Te JtT −1
0 1 0 [例2 - 3]已知A = 0 0 1 , 求e At 2 - 5 4
若
σ ω A= −ω σ
则
cos ωt sin ωt σt e = Φ(t ) = e − sin ωt cos ωt
At
2.2.4 计算
1.根据 e At 或 Φ (t ) 的定义直接计算
1 2 2 1 33 1 n n e = I + At + A t + A t ⋯ A t + ⋯ 2! 3! k! 1 0 [例2 - 1]已知A = , 求e At − 2 − 3
第二章现代控制理论状态空间表达式
diL R1 R1 R2 R2 = uC − iL + e(t ) dt L( R1 + R2 ) L( R1 + R2 ) L( R1 + R2 )
即
(2-11)
(3) 列出状态空间描述iL 1 − ( R + R )C 1 2 R1 L( R1 + R2 ) − R1 1 ( R1 + R2 )C uC ( R1 + R2 )C (2-12) + e(t ) R1 R2 iL R2 − L( R + R ) L( R1 + R2 ) 1 2
§2.1 状态空间描述的概念 2.1.2 控制系统的状态空间描述举例
例2-1 R-L-C系统，求其状态空间描述
R
u
L i
C
uC
解 (1) 确定状态变量 选择电容两端电压 uC (t )、电感通过的电流 i (t ) (2) 列写微分方程并化为一阶微分方程组 基尔霍夫（Kirchhoff）电压定律，
(2-13)
令
1 − ( R + R )C 1 2 A= R1 L( R + R ) 1 2
1 ( R + R )C 2 b= 1 R2 L( R + R ) 1 2
−
R1 ( R1 + R2 )C R1 R2 − L( R1 + R2 )
n 维列向量，状态向量
a12 a1n a22 a2 n an 2 ann
n×n方阵，系统矩阵(或状态矩阵)， 反映系统状态的内在联系
§2.1 状态空间描述的概念
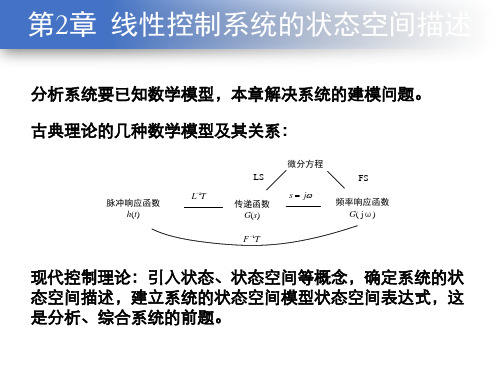
即
(2-11)
(3) 列出状态空间描述iL 1 − ( R + R )C 1 2 R1 L( R1 + R2 ) − R1 1 ( R1 + R2 )C uC ( R1 + R2 )C (2-12) + e(t ) R1 R2 iL R2 − L( R + R ) L( R1 + R2 ) 1 2
§2.1 状态空间描述的概念 2.1.2 控制系统的状态空间描述举例
例2-1 R-L-C系统，求其状态空间描述
R
u
L i
C
uC
解 (1) 确定状态变量 选择电容两端电压 uC (t )、电感通过的电流 i (t ) (2) 列写微分方程并化为一阶微分方程组 基尔霍夫（Kirchhoff）电压定律，
(2-13)
令
1 − ( R + R )C 1 2 A= R1 L( R + R ) 1 2
1 ( R + R )C 2 b= 1 R2 L( R + R ) 1 2
−
R1 ( R1 + R2 )C R1 R2 − L( R1 + R2 )
n 维列向量，状态向量
a12 a1n a22 a2 n an 2 ann
n×n方阵，系统矩阵(或状态矩阵)， 反映系统状态的内在联系
§2.1 状态空间描述的概念
现代控制理论第二章
第二章 控制系统状态空间表达式的解建立了控制系统状态空间表达式之后，就是讨论求解的问题，本章重点讨论状态转移矩阵的定义，性质和计算方法，从而导出状态方程的求解公式并讨论连续时间系统状态方程的离散化的问题。
§2-1线性定常齐次状态方程的解（自由解）所谓自由解是指系统输入为零时，由初始状态引起的自由运动。
状态方程为齐次矩阵微分方程：AX X= （2－1）若初始时刻0t 时的状态给定为00)(x t x =，则式（2-1）有唯一确定解。
0)(0)(x e t x t t A -=，0t t ≥（2－2）若初始时刻从0=t 开始，即0)0(x x =，则其解为：0)(x e t x At =， 0t t ≥（2－3）证：先假设式（2-1）的解)(t x 为t 的矢量幂级数形式，即：+++++=k k t b t b t b b t x 2210)(（2－4）对上式求导： ++++=-1232132)(k k t kb t b t b b t x代人式（2-1）得：A x= ( +++++kk t b t b t b b 2210) （2－5）既然式（2-4）是（2-1）的解，则式（2-5）对任意时刻t 都成立，故t 的同次幂项的系数应相等，有：01Ab b =，0212!2121b A Ab b ==，0323!3131b A Ab b ==，… 01!11b A k Ab kb k k k ==-，… 在式（2-4）中，令0=t ，可得：00)0(x x b == 将以上结果代人式（2-4），故得：022)!1!211()(x t A k t A At t x k k +++++= （2－6）括号内的展开式是n n ⨯矩阵，它是一个矩阵指数函数，记为At e221112!!At k ke At A t A t K =+++++ （2－7）式（2-6）可表示为：0()At x t e x =再用)(0t t -代替)0(-t ，即在代替t 的情况下，同样证明0)(0)(x e t x t t A -=的正确性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
而当AB≠BA是，则 这个性质说明，除非距阵A与B是可交换的，它们各目的矩阵指数函 数之积与其和的矩阵指数函数不等价。这与标量指数函数的性质是不同的。
2.2.3 几个特殊的矩阵指数函数 1．若 A 为对角线矩阵，即
EAST CHINA INSTITUTE OF TECHNOLOgy
(5)
则
(6)
2.若 A 能够通过非奇异变换予以对角线化，即
EAST CHINA INSTITUTE OF TECHNOLOgy
上式对
求解，即得式（12）。 时，则EAST CHINA INSTITUTE OF TECHNOLOgy
上式对 ，求异数，有：
再对 求异数，有：
重复以上步骤，最后有：
由上面的n个方程，对
2.2
矩阵指数函数——状态转移矩阵
满足初始状态 x(t ) |t 0 x(0) 的解是：
x(t ) eAt x(0)
A (t t0 )
满足初始状态 x(t ) |t t0 x(t0 )的解是： x(t ) e
At e Φ(t ) 则有： 令： A ( t t0 ) Φ(t t0 ) e
0 2 1 e 2t 1 1 e t e 2 t t 2t e 2e
3）用拉氏变换法求解
e At L1 ( sI A)1
EAST CHINA INSTITUTE OF TECHNOLOgy
s3 1 ( s 1)(s 2) s 1 1 sI A 2 2 s 3 ( s 1)(s 2)
EAST CHINA INSTITUTE OF TECHNOLOgy
2.1 线性定常齐次状态方程的解(自由解)
所谓系统的自由解，是指系统输入为零时，由初始状态引起的自由 运动。此时，状态方程为齐次微分方程：
(1)
若初始时刻 时的状态给定为 则式(1)有唯一确定解： (2) 若初始时刻从 开始，即 则其解为： (3) 证明： 级数形式 和标量微分方程求解类似，先假设式(1)的解 为 的矢量幂
EAST CHINA INSTITUTE OF TECHNOLOgy
(4) 代入式(1)得： (5)
既然式(4)是式(1)的解，则式(5)对任意时刻 都成立，故 的同次
幂项的系数应相等，有：
，可得：
EAST CHINA INSTITUTE OF TECHNOLOgy
在式(4)中，令
将以上结果代入式(4)，故得：
1 1 s 1 s 2 1 2 s 1 s 2
2e t e 2t t 2t 2 e 2 e
e t e 2t t 2t e 2e
例2-6，利用凯莱-哈密顿定理— -----------------自学！ 例2-3与例2-7也请注意自学！
求解，记得公式（13）。
例2-1，2-2，2-4：求以下矩阵A的状态转移矩阵 [解]： 1）直接算法（略） 2）用标准型法求解 特征值：
EAST CHINA INSTITUTE OF TECHNOLOgy
0 1 A 2 3
1 1, 2 2
1 1 1 2 1 2 2 1 2 1 P 1 1 1 1
x(t0 )
x(t ) Φ(t )x(0) x(t ) Φ(t t0 )x(t0 )
线性定常系统的状态转移矩阵
注：状态矩阵一般不是常数，而是时间的函数 起始矢量可以任意取，系统求解区间可任意选定—状态空间法的优点
2.2.2 状态转移矩阵(矩阵指数函数)的基本性质 1．性质一 或 这就是组合性质，它意味着从 转移到0，再从0转移到
(7)
EAST CHINA INSTITUTE OF TECHNOLOgy
3.若 A 为约旦矩阵 则
(8)
EAST CHINA INSTITUTE OF TECHNOLOgy
4.若
则
(9)
EAST CHINA INSTITUTE OF TECHNOLOgy
2.2.4 1.根据
的计算 的定义直接计算
At 0
t
A ( t )
Bu( )d
Φ(t )x(0) Φ(t )Bu( )d
0
t
EAST CHINA INSTITUTE OF TECHNOLOgy
Φ(t )x(0) Φ( )Bu(t )d
0
t
t 2 t t 2 t 2 e e e e At e Φ(t ) u (t ) 1 t 2t t 2t e 2e 2 e 2e t 2e e 2 e e 2 0 t d 2 2 0 Φ( )Bu(t )d 0 e 2 e 1 2e 2e t 1 2 t 1 t e e 2 e e d 2 2 2 0 e t 2t 2e e e 1 2t 1 t 2e t e 2t e t e 2t x1 (0) e e x(t ) 2 2 t 2t t 2t t 2t e 2e x2 (0) 2e e e e
矩阵指数函数——状态转移矩阵
2.2.1 状态转移矩阵 齐次微分方程(1)的自由解为： 或
令Φ(t ) eAt， 反应了由初始状态到时 间t的运动规律
该式反应了状态矢量由初始状态到任意时刻的矢量变换关系，反应了 状态矢量在空间随时间转移的规律，因此称为状态转移矩阵。
EAST CHINA INSTITUTE OF TECHNOLOgy
1 ( s 1)(s 2) s ( s 1)(s 2)
s3 At 1 ( s 1)(s 2) e L 2 ( s 1)(s 2)
1 1 2 ( s 1)(s 2) 1 s 1 s 2 L s 2 2 ( s 1)(s 2) s 1 s 2
EAST CHINA INSTITUTE OF TECHNOLOgy
(1)
的组合。
2.性质二 或 注：本性质可用于判断矩阵是否符合状态转移矩阵的条件 3.性质三 或 (3)
(2)
EAST CHINA INSTITUTE OF TECHNOLOgy
4.性质四 或 (4)
这个性质说明， 矩阵与A矩阵是可以交换的。 注：本性质还表明，由状态转移矩阵 可反推A！ 5.性质五 对于 方阵A和B，当且仅当AB=BA时，有
(6)
EAST CHINA INSTITUTE OF TECHNOLOgy
等式右边括号内的展开式是
矩阵，它是一个矩阵指数函数，记为 ，
即
(7) 于是式(6)可表示为：
再用 的正确性。
代替
即在代替
的情况下，同样可以证明式2)
EAST CHINA INSTITUTE OF TECHNOLOgy
2.2
故
EAST CHINA INSTITUTE OF TECHNOLOgy
对上式两边取拉氏反变换，从而得到齐次微分方程的解：
4.应用凯莱—哈密顿定理求 （1）由凯莱—哈密顿定理，方阵A满足其自身的特征方程，即
所以有
它是 同理
的线性组合。
EAST CHINA INSTITUTE OF TECHNOLOgy
编程，用计算机算，最终能得到收敛解。但很难得到解析解。例2-1 2.变换 A 为约旦标准型 （1）A 特征根互异
其中 T 是使 A 变换为对角线矩阵的变换阵。由式（7），有：
3.利用拉氏反变换法求
(10) 齐次微分方程
两边取拉氏变换 证明
即
EAST CHINA INSTITUTE OF TECHNOLOgy
At t A ( t ) 0
EAST CHINA INSTITUTE OF TECHNOLOgy
x(t ) e x(0) e
Bu( )d
Φ(t )x(0) Φ(t )Bu( )d
0
t
s3 ( s 1)(s 2) 1 sI A 2 ( s 1)(s 2)
第二章 控制系统状态空间表达式的解
2.1 2.2 2.3 线性定常齐次状态方程的解(自由解) 矩阵指数函数——状态转移矩阵 线性定常系统非齐次方程的解
EAST CHINA INSTITUTE OF TECHNOLOgy
2.4 * 线性时变系统的解 2.5 * 离散时间系统状态方程的解 2.6* 连续时间状态空间表达式的离散化
以此类推，
都可用
线性表示。
(2)在
定义中，用上面的方法可以消去 A 的 n及 n以上的幂次项， 即
（11）
（3）
的计算公式
EAST CHINA INSTITUTE OF TECHNOLOgy
A的特征值互异时，则
（12）
证明
根据A满足其自身特征方程的定理，可知特征值
和A是
可以互换的，因此， 也必须满足式（11），从而有：
e
At
1 ( s 1)(s 2) s ( s 1)(s 2)
e t e 2t t 2t e 2e
L
1
sI A
1
2e t e 2t t 2t 2 e 2 e
x(t ) e x(0) e
EAST CHINA INSTITUTE OF TECHNOLOgy
2.3
线性定常系统非齐次方程的解
现在讨论线性定常系统在控制作用 作用下的强制运动。此时状态