用MATLAB分析闭环系统的频率特性(1)
自动控制原理(第2版)(余成波_张莲_胡晓倩)习题全解及MATLAB实验第5章习题解答

第5章频率特性法频域分析法是一种图解分析法,可以根据系统的开环频率特性去判断闭环系统的性能,并能较方便地分析系统参量对系统性能的影响,从而指出改善系统性能的途径,已经发展成为一种实用的工程方法,其主要内容是:1)频率特性是线性定常系统在正弦函数作用下,稳态输出与输入的复数之比对频率的函数关系。
频率特性是传递函数的一种特殊形式,也是频域中的数学模型。
频率特性既可以根据系统的工作原理,应用机理分析法建立起来,也可以由系统的其它数学模型(传递函数、微分方程等)转换得到,或用实验法来确定。
2)在工程分析和设计中,通常把频率特性画成一些曲线。
频率特性图形因其采用的坐标不同而分为幅相特性(Nyquist图)、对数频率特性(Bode图)和对数幅相特性(Nichols图)等形式。
各种形式之间是互通的,每种形式有其特定的适用场合。
开环幅相特性在分析闭环系统的稳定性时比较直观,理论分析时经常采用;波德图可用渐近线近似地绘制,计算简单,绘图容易,在分析典型环节参数变化对系统性能的影响时最方便;由开环频率特性获取闭环频率指标时,则用对数幅相特性最直接。
3)开环对数频率特性曲线(波德图)是控制系统分析和设计的主要工具。
开环对数幅频特性L(ω)低频段的斜率表征了系统的型别(v),其高度则表征了开环传递系数的大小,因而低频段表征系统稳态性能;L(ω)中频段的斜率、宽度以及幅值穿越频率,表征着系统的动态性能;高频段则表征了系统抗高频干扰的能力。
对于最小相位系统,幅频特性和相频特性之间存在着唯一的对应关系,根据对数幅频特性,可以唯一地确定相应的相频特性和传递函数。
4)奈奎斯特稳定性判据是利用系统的开环幅相频率特性G(jω)H(jω)曲线,又称奈氏曲线,是否包围GH平面中的(-l,j0)点来判断闭环系统的稳定性。
利用奈奎斯特稳定判据,可根据系统的开环频率特性来判断闭环系统的稳定性,并可定量地反映系统的相对稳定性,即稳定裕度。
稳定裕度通常用相角裕量和幅值裕量来表示。
用MATLAB分析闭环系统的频率特性

用MATLAB分析闭环系统的频率特性闭环系统的频率特性指的是系统在不同频率下的响应特性。
在MATLAB中,可以通过不同的函数和工具箱来分析闭环系统的频率特性。
下面将介绍一些常用的方法。
1. 传递函数分析法(Transfer Function Analysis Method):传递函数描述了系统的输入和输出之间的关系。
在MATLAB中,可以使用tf函数创建传递函数对象,并利用bode函数绘制系统的频率响应曲线。
例如,假设有一个传递函数G(s) = 1/(s^2 + s + 1),可以用以下代码创建传递函数对象并绘制其频率响应曲线:```matlabG = tf([1], [1, 1, 1]);bode(G);```运行上述代码,将会显示出频率响应曲线,并且可以通过该函数的增益曲线和相位曲线来分析系统在不同频率下的响应特性。
2. 状态空间分析法(State-Space Analysis Method):状态空间模型描述了系统的状态变量之间的关系。
在MATLAB中,可以使用ss函数创建状态空间模型,并利用bode函数绘制系统的频率响应曲线。
例如,假设有一个状态空间模型A、B、C和D分别为:```matlabA=[01;-1-1];B=[0;1];C=[10];D=0;sys = ss(A, B, C, D);bode(sys);```运行上述代码,将会显示出频率响应曲线,并且可以通过该函数的增益曲线和相位曲线来分析系统在不同频率下的响应特性。
3. 伯德图法(Bode Plot Method):Bode图可以直观地表示系统的频率响应曲线。
在MATLAB中,可以使用bode函数绘制系统的Bode图。
例如,假设有一个传递函数G(s) =1/(s^2 + s + 1),可以用以下代码绘制其Bode图:```matlabG = tf([1], [1, 1, 1]);bode(G);```运行上述代码,将会显示出Bode图,并且可以通过该图来分析系统在不同频率下的增益和相位特性。
《过程控制》课后习题答案
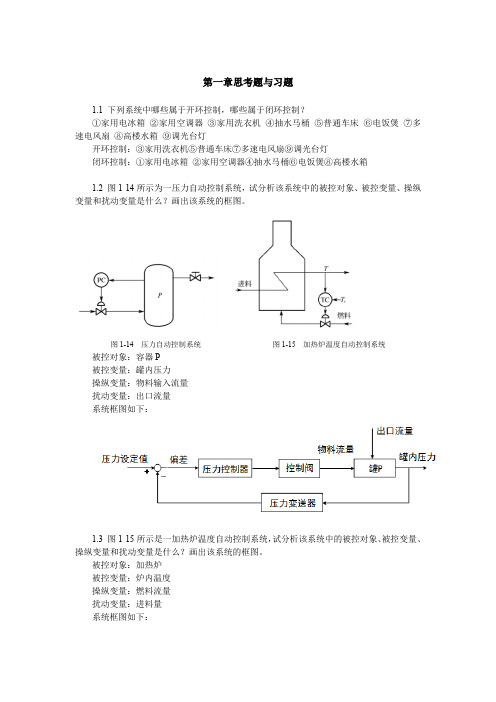
第一章思考题与习题1.1 下列系统中哪些属于开环控制,哪些属于闭环控制?①家用电冰箱②家用空调器③家用洗衣机④抽水马桶⑤普通车床⑥电饭煲⑦多速电风扇⑧高楼水箱⑨调光台灯开环控制:③家用洗衣机⑤普通车床⑦多速电风扇⑨调光台灯闭环控制:①家用电冰箱②家用空调器④抽水马桶⑥电饭煲⑧高楼水箱1.2 图1-14所示为一压力自动控制系统,试分析该系统中的被控对象、被控变量、操纵变量和扰动变量是什么?画出该系统的框图。
图1-14 压力自动控制系统图1-15 加热炉温度自动控制系统被控对象:容器P被控变量:罐内压力操纵变量:物料输入流量扰动变量:出口流量系统框图如下:1.3 图1-15所示是一加热炉温度自动控制系统,试分析该系统中的被控对象、被控变量、操纵变量和扰动变量是什么?画出该系统的框图。
被控对象:加热炉被控变量:炉内温度操纵变量:燃料流量扰动变量:进料量系统框图如下:1.4 按设定值的不同情况,过程控制系统分为哪几类?过程控制系统分为三类:定值控制系统、随动控制系统和程序控制系统。
1.5 什么是过程控制系统的过渡过程?有哪几种基本形式?过程控制系统从一个平衡状态过渡到另一个平衡状态的过程称为过程控制系统的过渡过程。
控制系统过渡过程有五种基本形式:发散振荡、单调发散、等幅振荡、衰减振荡和单调衰减。
1.6 某换热器的温度控制系统在单位阶跃干扰作用下的过渡过程曲线如图1-16所示。
试分别求出最大偏差、余差、衰减比、振荡周期和调整时间(设定值为200℃)。
图1-16 题1.6图最大偏差:30℃余差:5℃衰减比:5:1振荡周期:15min调整时间:22min第二章思考题与习题2.1 求取图2-55所示电路的传递函数,图中物理量角标i代表输入,o代表输出。
a)b)图2-55 习题2.1图a)(由分压公式求取)上式中,,。
b)上式中,,2.2 惯性环节在什么条件下可近似为比例环节?又在什么条件下可近似为积分环节?惯性环节在T很小的时候可近似为比例环节;T很大的时候条可近似为积分环节。
基于MATLAB的控制系统频率特性实验的开发_图文(精)

基于 MAT LAB 的控制系统频率特性实验的开发祁文哲王莉莉孟建军(兰州交通大学机电工程学院兰州 730070摘要设计了基于 MAT LAB 的虚拟实验系统 , 通过验证和试运行 , 此虚拟实验系统很好地实现了在计算机平台上频率特性实验的演示和仿真功能。
关键词自动控制原理 ; 频率特性 ; 虚拟实验系统 ;MAT LAB中图分类号 TP3D evelop i n g of Frequency Character isti i mBa sed on M(College of Lanzhan 730070, ChinaAbstract is on MAT LAB. The functi on of showing of the frequency char 2 acteristic and the on ol system is achieved perfectly by use .Key words p rincip le of aut o -contr ol; frequency characteristic; virtual experi ment system; MAT LAB1引言自动化是我国六大高新技术之一 , 而实验课是《自动控制原理》整个教学过程中不可缺少的重要组成部分 , 它可以将理论和实践紧密的联系起来 , 使学生加深对所学知识的理解。
我院传统的自动控制原理实验由于系统本身如电子器件的老化 , 接触不良 , 功能不全等缺点以及由于接线相对复杂 , 使得实验 , 尤其是频率特性的实验很难得到预期的效果 , 实验效率低 ; 随着各高校扩招 , 学生多、仪器少的问题更加突出 , 难以保证正常的实验教学。
因此我们的改进措施从硬件系统的改进开发入手。
教学设备从传统的“ 物理实验台” 转化到计算机平台上的“ 虚拟实验台” 是信息时代充分利用计算机技术和网络技术开展教学活动的一大特征。
我们利用 MAT LAB 强大的图形对象属性设置及 G U I 图形用户界面制作技术进行自动控制教学实验教学 , 开发实验系统。
5.4-1 and 5.4-2 闭环系统频域测试及辨识 [系统辨识理论及Matlab仿真]
![5.4-1 and 5.4-2 闭环系统频域测试及辨识 [系统辨识理论及Matlab仿真]](https://img.taocdn.com/s3/m/a64404f2ce2f0066f5332275.png)
5.4.1 基本原理
针对线性控制系统,要设计前馈控制器,传统的 方法是确定系统的闭环传递函数。采用建模方法难免 产生较大的建模误差。目前在实际应用中,更多的是 采用实验测试建模方法,即频率特性方法,通过频域 辨识技术来确定闭环系统的传递函数。
1
由闭环系统的正弦激励响应,通过最小 二乘方法和Bode图拟合来确定闭环系统的传 递函数。闭环系统测试框图如图1所示。
b0 0
(14)
显然,如果用不变性原理设计前馈控制器,则控制器表示为:
zd A z1 F z1
Bu z1 Ba z1
由于闭环系统的不稳定零点成为前馈控制器的极点,采用上式作为 控制器会造成控制系统不稳定。为了克服这种情况,对于闭环系统(13), 通过在控制器中引入零点 Bu (z) 来补偿闭环系统的不稳定零点 Bu (z1) , 设计零相差前馈控制器为:
图1 控制系统原理图 图2 等效框图
不失一般性,Gc (z1) 可以写成如下形式:
Gc
z 1
zd Bu z1 Ba A z1
z 1
(13)
其中, A(z1) 为分母多项式,其所有的根都位于单位圆内部。 d 为 非负整数,zd 为 d 步延迟。Bu (z1) 和 Ba (z1)为多项式, Bu (z1) 中
F
z 1
zd A
z 1
Bu z
Ba z1 Bu (1)2
(15)
5.4.3.2 系统相移
定理1[1] 对于(14)式定义的 Bu (z1) ,设H z1 Bu z Bu z1 ,则有:
(1) H e jT 0, R
应用MATLAB绘制系统频率特性曲线

G(s)
稳定性。
s3
5系s22.7统4s的 2奈奎斯特曲线,并利用曲线来判别闭环系统的
解 MATLAB仿真程序代码如下:
num1=[ 2.7];
den1=[1 5 4 2];
sys1=tf(num1,den1);
nyquist(sys1)
title('Nyquist图');
运行后,获得如图1-46所示曲线。
自动控制原理
应用MATLAB绘制系统频率特性曲线
1.1用MATLAB绘制系统开环对数频率特性 对于连续系统,用MATLAB函数绘制系统开环对 数频率特性的函数命令调用格式有 Bode(sys) Bode(sys,w) Bode(sys1,sys2,…,sysN) Bode(sys1,sys2,…,sysN,w) [mag,phase,w]=Bode(sys)
例1-15 绘制一阶惯性环节
的G(s奈) 奎3斯特图。
5s 1
解 MATLAB仿真程序代码如下:
G=tf(3,[5 1]);
nyquist(G);Fra bibliotekhold on;
title('Nyquist图');
运行后,获得如图1-45所示曲线。
图1-45 例1-15系统极坐标曲线图
例1-16 用函数nyquist(sys)绘制开环传递函数为
bode(num,den);hold on;
end
grid
获得振荡环节伯德图如图1-43所示,
图1-43 例1-13开环系统伯德图
如果希望求取控制系统的增益裕量 、相位GM裕量 界频率(也称PM交叉频
率) 、穿越g频率 ,可以使c 用margin函数 计算控制系统的相关稳定裕度值。
系统稳定性分析的仿真实验

系统稳定性分析的仿真实验一、实验目的:1.加深了解系统稳定性概念。
2.掌握使用Matlab 分析系统稳定性。
3.掌握使用Matlab 分析系统的频率特性二、实验设备:Matlab三、实验内容:1、已知控制系统开环传递函数为:17.18.01.023+++s s s K ,用Nyquist 稳定判据判定开环放大系数K 为10和50时闭环系统的稳定性。
2、已知控制系统开环传递函数为:()11.0)12.0(++s s s K ,取K =10,要求: ①绘制系统Bode 图,求出频域性能指标,并判断系统的稳定性;②改变开环增益K 值,分析K 变化对开环对数幅频、相频特性曲线的影响;③根据给出的稳定裕量,作K 参数设计,并评估系统性能。
四、实验步骤:实验内容一进入Matlab 命令窗口:1、当K=10时,输入命令num=[10]; %分子系数den=[0.1,0.8,1.7,1]; %分母系数g1=tf(num,den); %建立系统多项式模型nyquist(g1) %绘制Nyquist 图分析开环系统Nyquist 图,曲线是否包围(-1,j0)点?因此闭环系统稳定吗?2、当K=50时,输入命令num=[50]; %分子系数den=[0.1,0.8,1.7,1]; %分母系数g2=tf(num,den); %建立系统多项式模型nyquist(g2) %绘制Nyquist 图分析开环系统Nyquist 图,曲线顺时针包围(-1,j0)点几圈?表明闭环系统稳定性如何?有几个右半s 平面的极点?实验内容二K=10 K=50曲线未包围(-1,j0)点曲线包围(-1,j0)点一圈实验内容二①K=10,程序运行结果和图示可知,幅值裕度k= 1.5000 ,即 db;相位穿越频率wg=7.0711 rad/s;相角裕度r= 11.4304 ;幅值穿越频率wc= 5.7154 rad/s 。
②改变K值,分别取K为K1,K2,K3值时,观察系统的开环对数幅频、相频特性曲线的变化,分析K值变化对其影响。
自动控制原理的MATLAB仿真与实践第5章 线性系统的频域分析

函数模型,如:tf(), zpk(), ss()。 bode(num,den):num,den分别为传递函数的分子与
margin(G);[Gm,Pm,Wcg,Wcp]= margin(G): 直接求出系统G的幅值裕度和相角裕度。 其中:Gm幅值裕度;Pm相位裕度;Wcg幅值裕度 处对应的频率ωc;Wcp相位裕度处对应的频率ωg。
nichols(G);nichols(G,w):绘制单位反馈系统开环传 递尼科尔斯曲线。
20
>>clear; num=[2, 3];den=[1, 2, 5, 7]; %G(s)的分子分母 多项式系数向量
p=roots(den) 求根结果:
%求系统的极点
p=
-0.1981 + 2.0797i
-0.1981 - 2.0797i
-1.6038 可见全为负根,则s右半平面极点数P=0。 绘制Nyquist曲线: >> nyquist(num,den) %绘制Nyquist曲线
本节分别介绍利用MATLAB进行频域绘图和频 率分析的基本方法。
6
5.2.1 Nyquist曲线和Bode图
MATLAB频率特性包括幅频特性和相频特性。 当用极坐标图描述系统的幅相频特性时,通常称为 奈奎斯特(Nyquist)曲线;用半对数坐标描述系 统的幅频特性和相频特性时,称为伯德(Bode) 图;在对数幅值-相角坐标系上绘制等闭环参数( M和N)轨迹图,称为尼克尔斯(Nichols)图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用MATLAB 分析闭环系统的频率特性
1、等M 圆图与等N 圆图原理
1.1设有单位系统如图1示。
其闭环频率特性G B (j )与开环频率特性G K (j )的关系为 )(j G 1)(j G )(j X )(j X )(j G K K i 0B ωωωωω+== (1)
图 1
可将其开环频率特性G K (j )写成
G K (j
)=U ()+jV() (2) 则闭环频率特性为
)(j B )e M(jV
U 1jV U )G (j 1)G (j )(j G ωαωωωω=+++=+= (3) 式中 M()——闭环的幅频特性
()——闭环的相频特性 闭环的幅频特性为
2
12222V )U (1V U |jV U 1||jV U |M ⎥⎦⎤⎢⎣⎡++++++= (4) 所以 222
22
V U)(1V U M +++= (5) 则有 2
22
2222
1)-(M M V )1-M M (U =++ (6) 显然,式(6)是一个元的方程,他表明了开环的实频U 、虚频V 和闭环的幅频M 之间
G K (j )
X i (j )
X 0(j )
的的关系,该圆方程的圆心坐标为(1M M 22--,j0),半径为|1-M M |2。
当M 取不同的值时,便可以得到一簇圆,如图1,该图称为等M 圆图(邮称为等幅值轨迹图)。
有闭环的相频特性为
)V
U U V (tg )U 1V (tg )U V (tg )jV U 1jV U (221-1-1-++=+=+++∠=-α (7) 令22V
U U V tg N ++==α,上式可改为 22224N
1N )2N 1(V )21(U +=+++ (8) 可见式(8)也是一个圆方程,他表明了U 、V 与N 之间的关系。
该圆方程的圆心坐标为
|。
-,半径为|-1N )2N 1j ,21(2当N 取不同的值时,可画出一簇圆,如图2所示。
该
方法复杂,也不准确,我们用一个具体的力来说明一下用MATLAB 解决这类问题的方
法。
[例]求开环频率特性为1)
1)(0.2j (0.05j j 3)(j G k ++=
ωωωω的单位反馈系统的闭环频率特性。
2、用MATLAB 解决闭环系统频率特性 <以G(s)=10/s(s+1)(s^2/4+1)为例
这种传递函数是零极点描述形式,因而要使用sys=zpk(z,p,k)的命令形式 其中,z 为传递函数的零点向量[z1,z2,z3,...],描述形式为(s-z1)(s-z2)...
p 为传递函数的极点向量,k 为增益,因而在该例中,应首先化为标准形式,即 G(s)=40/s(s+1)(s+2i)(s-2i),于是有(在命令行输入)
k=40;z=[];p=[0 -1 -2i 2i];
sys=zpk(z,p,k);就得到了传递函数>
例题的开环传递函数为 )
5)(20(300)(++=s s s s G 用MATLAB 编程和运行结果如下:
%MATLAB PROGRAM
%Create system model
sys=zpk([],[0 -20 -5],300);
sysclose=feedback(sys,1);
%Get frequency response of the system
w=logspace(-1,2);
bode(sysclose,w)
[mag,phase,W]=bode(sysclose,w);
[l,c]=size(mag);
mag1=zeros(c,1);
for i=1:c
mag1(i)=20*log10(mag(1,1,i)); end
%显示系统闭环的幅值穿越频率
disp('crossover frequency:');
Wc=interp1(mag1,W,0,'spline')
%显示谐振频率
disp('Resonance frequency:'); [mag2,i]=max(mag1);
Wr=W(i)
%显示谐振峰值
disp('Resonance magnitude:') Magmax=mag2
%显示-3dB截止频率
disp('-3dB frequency:');
W_3db=interp1(mag1,W,-3,'spline') [l,c]=size(phase);
pha1=zeros(c,1);
for i=1:c
pha1(i)=phase(1,1,i);
end
%显示-90度截止频率
disp('-90 phase frequency:');
W_90=interp1(pha1,W,-90,'spline')运行结果:
>> crossover frequency:
Wc =
0.1763
Resonance frequency:
Wr =
2.5595
Resonance magnitude: Magmax =
0.7477
-3dB frequency:
W_3db =
9.5479
-90 phase frequency:
W_90 =
3.4641
如果在上述的M文件中再加下面几行,可以绘制Bode图并在图中标出幅值裕度和相位裕度,以及可求出相位角阶频率W cg和幅值交界频率W cp,W cg是指Bode图的相频曲线穿越-180时的频率,W cp是指Bode图的幅值曲线穿越0分贝线时的频率。
figure(2)
margin(sys)
[Gm,Pm,Wcg,Wcp]=margin(sys)
运行结果为:
Gm =
8.3333
Pm =
54.7410
Wcg =
10.0000
Wcp =
2.6320
由此我们可以很容易的判断系统的稳定性。
3、结束语
MATLAB是一种面向科学和工程计算的计算机语言,它具有强大的计算功能、计算结果和编程可视化及极高的编程效率,它包含有几十个工具箱,可以直接调用各种函数,是计算简单且精确。
本文就是利用编写MATLAB的M文件,来解决控制问题,使以前复杂的问题得到了简化。
