46 理想稀溶液液态混合物
物化各种公式概念总结

第一章热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
二、基本定律 热力学第一定律:ΔU =Q +W 。
三、基本关系式1、体积功的计算 δW = -p 外d V恒外压过程:W = -p 外ΔV定温可逆过程(理想气体):W =nRT 1221ln ln p p nRT V V = 2、热效应、焓:等容热:Q V =ΔU (封闭系统不作其他功)等压热:Q p =ΔH (封闭系统不作其他功)焓的定义:H =U +pV ; ΔH =ΔU +Δ(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容:热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂= 定压热容与定容热容的关系:nR C C =-V p热容与温度的关系:C p ,m =a +bT +cT 2四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p 外d V等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d pC V (㏑T 2-㏑T 1)=nR(㏑V 1-㏑V 2)(T 与V 的关系)C p (㏑T 2-㏑T 1)=nR(㏑P 2-㏑P 1) (T 与P 的关系)不可逆绝热过程:Q =0 ;利用C V (T 2-T 1)=-p 外(V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化 可逆相变化:ΔH =Q =n ΔH ; W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、实际气体节流膨胀:焦耳-汤姆逊系数:μJ-T (理想气体在定焓过程中温度不变,故其值为0;其为正值,则随p 降低气体T 降低;反之亦然)4、热化学标准摩尔生成焓:在标准压力和指定温度下,由最稳定的单质生成单位物质的量某物质的定压反应热(各种稳定单质在任意温度下的生成焓值为0) 标准摩尔燃烧焓:…………,单位物质的量的某物质被氧完全氧化时的反应焓第二章 热力学第二定律一、基本概念 自发过程与非自发过程二、热力学第二定律热力学第二定律的数学表达式(克劳修斯不等式)T Q dS δ≥ “=”可逆;“>”不可逆三、熵(0k 时任何纯物质的完美结晶丧子为0)1、熵的导出:卡若循环与卡诺定理(页522、熵的定义:T Q dS r δ=3、熵的物理意义:系统混乱度的量度。
理想稀溶液 理想溶液 活度

3.4.1 理想稀溶液如前所述,稀溶液中溶剂的蒸气压服从拉乌尔定律,溶质服从亨利定律。
但是, 溶液“稀”到什么程度才能服从这两个定律呢?目前没有一定的界限,这随溶液不同而不同。
凡是完全符合这两个定律的稀溶液称为理想稀溶液。
从理论上讲,浓度极低,即无限稀溶液必然是理想稀溶液。
一种溶液“稀”到什么程度才能称为理想稀溶液需要通过实验才能确定。
3.4.2 理想溶液1、理想溶液的定义如果溶液中任一组元在全部浓度范围内都服从拉乌尔定律,这种溶液称为理想溶液。
从微观上讲,要满足理想溶液的定义,各组元的分子体积应当相差不多,不同组元质点间相互作用力与同一组元质点间相互作用力相差不大,形成溶液时,也无离解、缔合等作用发生。
严格地说,真正的理想溶液是很少的。
但是由于理想溶液所服从的规律比较简单,常常把有些溶液(比如,G e-M n、G e O-M n O等溶液)近似地看作理想溶液。
2、理想溶液的热力学性质(1)理想溶液各组元的蒸气压和蒸气总压都与组成成直线关系;(2)理想溶液组元的化学位服从以下简单关系(3)理想溶液由于各组元的体积相差不大,而且混合时相互吸引力没有变化,因此混合前后体积不变;(4)由于理想溶液各组元分子间的相互作用力不变,其混合热等于零;(5)理想溶液的混合熵只决定于克分子分数,与溶液各组元的本性无关,即符合以下关系△S M=-R∑x i lnx i(3.24)(6)理想溶液的混合自由能为△F M=RT∑x i lnx i(3.25)3.4.3 实际溶液对理想溶液的偏差理想溶液各组元在任何浓度都服从拉乌尔定律。
而事实上,大多数实际溶液都对拉乌尔定律有偏差,即蒸气压大于或小于拉乌尔定律的计算值。
如果蒸气压大于拉乌尔定律的计算值,称为正偏差;反之,如果蒸气压小于拉乌尔定律的计算值,叫做负偏差。
1、负偏差图3.1为Mg-Pb二元系在一定的温度下蒸气压与组成之间的关系图,图中虚线为拉乌尔定律的理论蒸气压线,实线为实测值。
多组分系统热力学与相平衡
度,单位是mol/m3,但常用单位是mol/dm3。
4.质量分数wB
wB
mB m(总)
溶质B的质量与溶液总质量之比称为溶 质B的质量分数,无单位。
§5-2 稀溶液中的两个经验定律
一、拉乌尔定律 1886年,法国化学家Raoult从实验中归纳出 一个经验定律:在定温下,在稀溶液中,溶 剂的蒸气压等于同温下纯溶剂的饱和蒸气压 PA*乘以溶液中溶剂的物质的量分数xA。 用公式表示为:
2. 若溶液中有B、C、 D等物质同时存在,平衡时
B
(l,T
,
p,
xc
)
B
(g,T
,
p,
yc
)
B
(T
)
RT
ln(
pB p
)
在上两式中消去 B (T),则得
B
(l,T
,
p,
xc
)
B
(T
,
p)
RT
ln(
pB pB
)
Q pB pB xB
B (l,T , p, xc ) B (T , p) RT ln xB
例1试说明下列平衡系统的自由度数。 (1) 25℃及标准压力下,NaCl(s)与其水溶液平 衡共存; (2) I2 (s)与I2 (g)呈平衡; (3)开始时用任意量的HCl (g)和NH3 (g)组成的 系统中: 反应 HCl (g)+NH3 (g)= NH4Cl (s)达到平衡。
解(1)C=2 ; F=2-2+0=0 指定温度,压力,饱和食盐水的浓度为定 值,系统无自由度。
bB def
nB mA
溶质B的物质的量与溶剂A的质量之比称为溶
物理化学上册名词解释

1、理想气体在微观上具有两个特征1分子间无相互作用力2分子本身不占有体积2、道尔顿定律混合气体的总压力等于各组分单独存在于混合气体的温度,体积条件下的产生压力的总和3、饱和蒸汽压:单位时间内有液体分子变为气体分子的数目与气体分子变为液体分子数目相同,宏观上说即液体的蒸发速度与气体的凝结速度相同的气体称为饱和蒸汽,饱和气体所具有的压力称为饱和蒸汽压。
4、临界温度每种液体都存在一个特殊的温度,在该温度上,无论加多少大压力,都不在能使气体液化,临界温度是使气体能够液化所允许的最高温度。
5、超临界流体:当物质处在稍高于临界温度和压力的状态时,既不是一般意义上的气体,也不是液体,而称为超临界流体是一种高密度流体,具有气体与液体的双重特性,其黏度与气体相似,但密度却和液体相近,而扩散系数比液体大得多。
6、波义尔温度:任何气体都有一个特殊的温度Tb,称为波义尔温度,在波义尔温度,pvm-p等温线的斜率在压力趋于零时为零,故波义尔温度定义为7、第二维里系数反映了两个气体分子间的相互作用对气体pvt 关系的影响,第三维里系数则反映了三分子相互作用引起的偏差。
8、广度量是指与物质的数量成正比的性质,如系统物质的量,体积,热力学能,熵等。
具有加和性,在数学上是一次齐函数,而强度量是指与物质无关的性质,如温度压力等9、系统处在平衡态条件1系统内部处于热平衡,2力平衡3相平衡4化学平衡3 4合并为物质平衡10、摩尔相变焓是指单位物质的量的物质在恒定温度T及该温度平衡压力下发生相变时对应的焓变11、标准摩尔生成焓在温度为T的标准态下,由稳定相态的单质生成化学计量数VB=1的β相态的化合物B 该生成反应的焓变称为该化合物B在温度T时的标准摩尔生成焓。
12、节流膨胀的热力学特征:1气体的始末态压力分别保持恒定不变且始态压力大于末态压力2过程绝热Q=0 。
3恒焓过程4真实气体经节流膨胀后产生致冷或致热效应是H=f(T,p)这一关系的必然结果。
稀溶液中的两个定律

饱和蒸汽压0.3167 kPa,求从海水中取1mol水需最小非体
积功?
解:
1mol 海水 GT , p
1mol 纯水
混合的逆向行为
Gm=W’
Gm = (纯水)- (海水)
= * -(* + RT lnx水 )
= - RT lnx水
p水 p水* x水
RT
ln
p水 p水*
= - 8.314 × 298 × ln(0.306 / 0.3167)
3.理想液态混合物的通性
偏摩尔性质
(1)偏摩尔体积
GB p
T ,n
B
p
T ,n
VB
B
p
T ,n
VB
B
(T
,
p)
B
(T
,
p)
RT
ln
xB
两边等T 对压力求导 VB VB
(2)偏摩尔焓
HB
H
B
(可由Gibbs-Helmholtz公式证明)
B
(T
,
p)
B
(T
,
p)
RT
ln
xB
B (T ,
V
RTcB
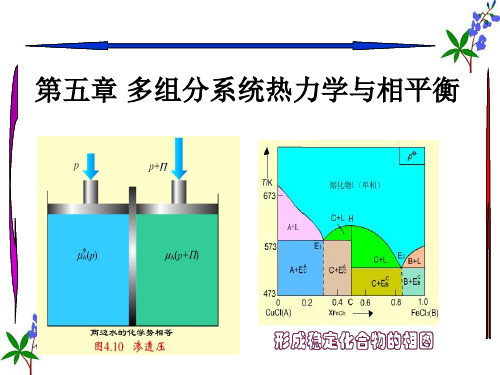
• 渗透压,阻止水分子渗透必须外加的最小压力
• 若外加压力大于渗透压,水分子向纯水方渗透, 称为反渗透,可用于海水淡化,污水处理等。
稀溶液的依数性
1. 蒸气压下降 2. 凝固点下降 3. 沸点升高 4. 渗透压
pA p*A xB
Tf K f mB Tb KbmB
RTcB
溶质的粒子--分子、离子、大分子或胶粒
p*A pA p*A xB
pA p*A xB
2. 凝固点降低 Freezing-point depression
热力学公式汇总

物理化学主要公式及使用条件第一章 气体的pVT 关系 主要公式及使用条件1. 理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ,V ,T 及n 单位分别为Pa ,m 3,K 及mol 。
m /V V n =称为气体的摩尔体积,其单位为m 3 · mol -1。
R = J · mol -1 · K -1,称为摩尔气体常数。
此式适用于理想气体,近似地适用于低压的真实气体。
2. 气体混合物 (1) 组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B *=V ϕ∑*AV y A m ,A式中∑AA n 为混合气体总的物质的量。
Am,*V表示在一定T ,p 下纯气体A 的摩尔体积。
∑*AA m ,A V y 为在一定T ,p 下混合之前各纯组分体积的总和。
(2) 摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量,∑=BB n n 为混合气体总的物质的量。
上述各式适用于任意的气体混合物。
(3)V V p p n n y ///B B B B *=== 式中p B 为气体B ,在混合的T ,V 条件下,单独存在时所产生的压力,称为B 的分压力。
*B V 为B 气体在混合气体的T ,p 下,单独存在时所占的体积。
3. 道尔顿定律p B = y B p ,∑=BB p p上式适用于任意气体。
对于理想气体V RT n p /B B =4. 阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。
第二章 热力学第一定律 主要公式及使用条件1. 热力学第一定律的数学表示式W Q U +=∆或 'amb δδδd δdU Q W Q p V W =+=-+规定系统吸热为正,放热为负。
系统得功为正,对环境作功为负。
讨论1.通常意义的稀溶液(浓度很小)都是理想稀溶液吗2.理想.

即稀溶液中,溶剂的蒸气压的下降 pA 值与溶液中溶质的摩尔分数成正比。
右图是溶剂 A的蒸气压与温度的关系
曲线:由于溶液的蒸气压只是 A 的
蒸气压,小于纯溶剂 A 在同温度的
蒸气压。所以其蒸气压曲线 oc 在纯
o
A 蒸气压曲线 oc下方。Δp是一定组
K 称为分配系数
对稀溶液,同样有:Kc = cB()/cB() (3.6.19)
若 B 在 相及 相中的存在形式不一样,例在 相中以单 分子形式存在,在 相中以单、双分子两种形式存在,则, 分配定律的形式,与上不同。
§3.7 稀溶液的依数性 colligative properties
c c
o
o a
因为,溶液中 A 的蒸气压低于纯液 体A的蒸气压,所以溶液中 A 的蒸气 压曲线自然与纯固态 A 的蒸气压相 交于较低的位置 o,所对应的温度Tf 低于纯液态 A 的凝固点 Tf 。
Tf Tf Tf 0
被称为溶液的凝固点降低值。
Tf Tf
T
下面,用热力学原理推导凝固点降低值与溶液组成的定量关系。
若外压为标准压力,则称为标准熔点。
对于纯物质,在同样压力下,其凝固点与熔点是相同的。
溶液或液态混合物的凝固点:在一定外压下,一定组成的 溶液或液态混合物被冷却而开始析出固体的平衡温度,称为 该溶液或液态混合物的凝固点。
它不仅与溶液或液态混合物的组成有关,还与析出固相 的组成有关。在此,只讨论从溶液或液态混合物中仅析出固 态纯溶剂A,而溶质 B 并不随A以固态溶液形式析出的简单 情况
p,bB
SA(l)
μA(l)
主要化学势表达式的识记关系

=+00pg)g)ln()*pμ(μ(RT p)ln((g (pg)0B0BB pp RT )μμ+=`前面不变,只是对数项=+00pg)g)ln()*pμ(μ(RT p前面不变,只是对数项中的压力p 改逸度f 。
主要化学势表达式的识记关系丽水学院化学化工系课程中主要学习的化学势可分为气体化学势,理想液态混合物化学势及非理想液态混合物化学势,理想稀溶液化学势及非理想稀溶液化学势。
为了便于大家记忆,对各种化学势表达式进行概括。
一、气体化学势的识记关系1.以纯理想气体化学势为基础。
其化学势表达式为:式中,p g 表示理想气体,*表示纯态。
(g)0μ为气体的标准化学势。
真实气体标准态与理想气体标准态均规定为纯理想气体状态,其压力为标准压力 0p = 100 kPa 。
2.纯理想气体与混合理想气体中B 组分化学势的对比关系图:其中,总p y p B B = 为B 的分压。
3.纯理想气体与纯实际气体的化学势表达式对比关系图:=+00pg)g)ln()*pμ(μ(RT pμB (l ) =;其中,f =γp ,f 称逸度,可理解为修正后的压力,γ称逸度系数。
4.混合理想气体中B 组分的化学势与混合实际气体化学势表达式的对比关系图:二、理想液态混合物化学势及非理想液态混合物化学势,理想稀溶液化学势及非理想稀溶液化学势的识记关系。
1.气、液相同组分化学势关系的建立:当气体相是混合气体,且可看作是理想气体时,则气、液两相达平衡时,两相中同一组分B 的化学势相等,即: [此式适用于任何两相平衡体系,理想液态混合物化学势及非理想液态混合物化学势,理想稀溶液化学势及非理想稀溶液化学势公式都可在此式的基础上建立。
2.理想液态混合物中任一组分的化学势表达式因为,理想液态混合物中任一组分均遵守拉乌尔定律:p B =p B *x B 。
)ln((g (pg)0B0BB pp RT )μμ+=前面相同,只是对数项中的分压p 改分逸度f B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V VB n B
T , p ,ni
2.偏摩尔量的定义与物理意义
对容量性质X, 根据状态函数的基本假定
X X (T , p, nB , nC , nD )
X X X dX dT dp dnB B nB T , p , n T p ,nB ,nC p T ,nB ,nC C
3.偏摩尔量的测定法举例
以二组分体系的偏摩尔体积为例,说明
测定偏摩尔量的方法原理
n1V1,m n2V2,m V Vm X1V1,m X 2V2,m n1 n2 n1 n2
偏摩尔量的实验测定
以偏摩尔体积为例:
T、P一定,向物质的量 为nC的液体C中,不断 加入B形成混合物,以混 合物体积V和B的物质的 量nB作图。图中任一点 作曲线的切线,其斜率 即为偏摩尔体积
水和乙醇混合
水和乙醇混合
偏摩尔体积 在一定温度压力下,单位物质的量的组分B在确 定组成的混合物中对体积的贡献量VB,等于在无 限大量该组成的混合物中加入单位物质的量的 B(混合物组成未变)引起系统体积的增加值,也 等于在有限量的该组成的混合物中加入dnB的B (混合物组成未变)引起系统体积增加量dV折合成 加入单位物质的量的B时的增量,称为物质B的 偏摩尔体积。数学表达式为
内能等)在纯物质体系具有与质量相同的这种性质;
等温等压下将多种纯物质混合形成多组分体系,往
往伴随有容量性质的变化。
以偏摩尔体积为例
将纯液体B与C混合,其摩尔体积分别为Vm,B和Vm,c,对于理想 液体
V nBVm,B nCVm,C
对于真实பைடு நூலகம்体
V nBVm, B nCVm,C
原因:B、C分子的大小不同,分子间作用力(B-B,C-C,B-C) 不同。
1atm 25 ℃
(nV) nVH2O(纯)
Ⅹ
3
0.006 18.02 0.108cm
0.006 16.5 0.099cm
水
1mol水 1mol甲醇
( nV ) n[V H2O ( x
] 0.5 )
3
√
• 例 2:在 1atm 、 25 ℃条件下, x1=0.3 的甲醇( 1) 水( 2 )混合物中,加入 0.1mol 的水,测得混合物 体积增加了1.78cm3。已知水的摩尔性质为V2=18.02 ( cm3 mol-1),求水的偏摩尔体积与纯水摩尔体积之 差。 ( nV ) 解: Vi [ ]T , P ,n j i ni
物理化学
第四章 多组分系统热力学
Thermodynamics of Multicomponent Systems
学习要求:
理解偏摩尔量和化学势的定义、性质。掌握化学 势的计算以及表达式中的参考态与标准态。 掌握拉乌尔(Raoult)定律和亨利(Henry)定律的 表述与数学表达式。 掌握理想混合物的概念、性质以及任一组分化学 势表达式。 掌握理想稀溶液概念及溶剂溶质的化学势表达式。 理想稀溶液的依数性。 了解实际气体的逸度与逸度系数以及实际溶液的 活度与活度系数的概念。
X X (T , p, nB , nC , nD )
对纯组分系统 来说偏摩尔量就是它的摩尔量。 只有容量性质才有偏摩尔量,强度性质没有; 只有恒温恒压下系统容量性质随物质的量的变 化率才称为偏摩尔量。
一般式有
U H A S G
nBU B
B
UB ( HB
U )T , p , nC (C B ) nB
第四章
4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9
多组分系统热力学 引言
偏摩尔量 化学势 气体组分的化学势 拉乌尔定律和亨利定律 理想液态混合物 理想稀溶液 稀溶液的依数性 逸度与逸度因子 活度与活度因子
§41 偏摩尔量
1.问题的提出
无论什么体系,体系质量总是等于构成该体 系各物质的质量的总和。其它容量性质(如体积、
n
B B
B
n
B
=B
练习题
下述各量中,哪些是偏摩尔量?( ) A. √
H n B T , P ,nC
B.
U n B
T ,V ,nC
A p C. T ,V ,nC
G D.
T p ,V ,nC
n
B
B
HB
H ( )T , p , nC (C B) nB
n
B
B
AB SB GB
A AB ( )T , p , nC (C B ) nB S SB ( )T , p , nC (C B ) nB G GB ( )T , p , nC (C B) nB
nV nV 1.78 3 17.8cm / mol V2 n n2 T , P ,n1 2 T , P ,n 0.1
1
答:纯水与其偏摩尔体积之差是 18.02-17.8=0.22(cm3 mol-1) ,对于0.1mol的水,体积差是0.022cm3;
V E. √
nB T , p ,nC
H F.
nB S , p ,nC
例1: 已 知 1atm, 25 C下VH2O( 纯 ) 18.02cm3 / mol; V H2O ( x水 0.5 ) 16.52cm3 / mol 问向杯中加入 0.006mol水 后, 溶 液 体 积 增 加 多 少 ? ( nV ) 解: Vi [ ]T , P ,n j i ni 0.006molH2O
偏摩尔量
XB
def
X n B T , p , nC
X X dX dT dp X BdnB B T p ,nB p T ,nB
偏摩尔量的性质
偏摩尔量是在无限大的系统恒定T,p 和其它物质的
量时,改变1mol 物质B引起的系统容量性质X的变化。
