专题19-平行四边形、矩形、菱形--拔高题
平行四边形,矩形,菱形的存在性问题(有答案)

平行四边形,矩形,菱形的存在性问题一、平行四边形存在性问题1.在平面直角坐标系中,点A,B,C的坐标分别是A(﹣1,3),B(﹣5,﹣3),C(1,﹣3),在平面内找一点D,使四边形ABCD是平行四边形,则点D的坐标是.2.已知平行四边形ABCD的两条对角线相交于平面直角坐标系中的原点O,点A(﹣1,3),B(1,2),则点C,D的坐标分别为.3.在直角坐标系中,点A、B的坐标分别为(﹣2,4)、(﹣5,2),点M在x轴上,点N 在y轴上.如果以点A、B、M、N为顶点的四边形是平行四边形,那么符合条件的点M 有个.4.如图,在平面直角坐标系中,AD∥BC,AD=5,B(﹣3,0),C(9,0),E是BC的中点,P是线段BC上一动点,当PB=时,以点P、A、D、E为顶点的四边形是平行四边形.第4题第5题第6题5.如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y 的正半轴上,且OB=2OC,在直角坐标平面内确定点D,使得以点D、A、B、C为顶点的四边形是平行四边形,请写出点D的坐标为.6.如图,已知A(1,0)、C(0,1)、B(m,0)且m>1,在平面内求一点P,使得以A、B、C、P为顶点的四边形是平行四边形,则点P的坐标为.7.已知点A(4,0),B(0,﹣2),C(a,a)及点D是一个平行四边形的四个顶点,则线段CD长的最小值为.8.(1)在图1,2,3中,给出平行四边形ABCD的顶点A,B,D的坐标(如图),图1,2,3中的顶点C的坐标分别是,,;(2)在图4中,若平行四边形ABCD的顶点A,B,D的坐标分别为(4,1)、(3,4)、(6,4),则顶点C的坐标为;(3)在图4中,平行四边形ABCD顶点坐标分别为A(a,b)、B(c,d)、C(m,n)、D(e,f),则其横坐标a,c,m,e之间的等量关系为;纵坐标b,d,n,f之间的等量关系为.9.如图,矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是(6,8),将矩形OABC沿直线BD折叠,使得点C恰好落在对角线OB上的点E处,折痕所在直线与y 轴、x轴分别交于点D、F.(1)请直接写出线段BO的长;(2)求折痕所在直线BD的解析式;(3)若点M在直线y=﹣x上,则在直线BD上是否存在点P,使以C、D、M、P为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点P的坐标;否则,请说明理由.二、矩形存在性问题10.在平面直角坐标系中,已知点A(0,0),B(2,﹣2),C(4,0),D(2,2),则以这四个点为顶点的四边形ABCD是()A.矩形B.菱形C.梯形D.正方形11.如图1,在四边形ABCD中,AB∥CD,∥BCD=90°,AB=AD=10cm,BC=8cm.点P 从点A出发,以每秒3cm的速度沿线段AB方向向B运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时出发,当点P运动到点B 时,P、Q同时运动停止,设运动时间为t秒.(1)求CD的长;(2)当t为何值时,四边形PBQD为平行四边形?(3)在运动过程中,是否存在四边形BCQP是矩形?若存在,请求出t的值;若不存在,请说明理由.12.平行四边形AOBC在平面直角坐标系中的位置如图(1).(1)写出点C的坐标;(2)在图(1)中,连接AB,OC得到图(2),求AB与OC的交点M点的坐标;(3)将图(2)中的线段BC向两方延长得到图(3),若点D,E为直线BC上不与B,C重合的动点,是否存在这样的D,E点,使得四边形OADE为矩形?若存在,请在图中画出矩形,并求出矩形OADE的面积和点D,E的坐标,若不存在,请说明理由.三、菱形存在性问题13.在直角坐标系中,A,B,C,D四个点的坐标依次为(﹣1,0),(x,y),(﹣1,5),(﹣5,z),若这四个点构成的四边形是菱形,则满足条件的z的值有()A.1个B.3个C.4个D.5个14.如图1,直线l1:y=﹣x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.(1)求A,B两点的坐标;(2)求∥BOC的面积;(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO 方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.∥当OA=3MN时,求t的值;∥试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.参考答案1.根据题意得:D点的纵坐标一定是3;又由C点相对于B点横坐标移动了1﹣(﹣5)=6,故可得点D横坐标为﹣1+6=5,即顶点D的坐标为(5,3).2.由题意知:点A与点C、点B与点D关于原点对称,∥点A,B的坐标分别为(﹣1,3),(1,2),∥点C,D的坐标分别是(1,﹣3),(﹣1,﹣2),3.有3个点.4.解:∥B(﹣3,0),C(9,0),∥OB=3,OC=9,∥BC=OB+OC=12,∥E是BC的中点,∥BE=CE=BC=6,分为两种情况:∥当P在E的左边时,∥AD=PE=5,CE=6,∥BP=12﹣6﹣5=1;∥当P在E的右边时,∥AD=EP=5,∥BP=BE+EP=6+5=11;即当BP为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;故答案为:1或11.5.如图,∥当BC为对角线时,易求M1(3,2);∥当AC为对角线时,CM∥AB,且CM=AB.所以M2(﹣3,2);∥当AB为对角线时,AC∥BM,且AC=BM.则|M y|=OC=2,|M x|=OB+OA=5,所以M3(5,﹣2).综上所述,符合条件的点D的坐标是M1(3,2),M2(﹣3,2),M3(5,﹣2).6.根据题意得:OA=OC=1,OB=m,∥AB=m﹣1,分三种情况:如图所示,∥以BC为对角线时,点P的坐标为(m﹣1,1);∥以AC为对角线时,点P的坐标为(1﹣m,1);∥以AB为对角线时,点P的坐标为(m+1,1);综上所述:点P的坐标为(m﹣1,1)或(1﹣m,1)或(m+1,﹣1);故答案为:(m﹣1,1)或(1﹣m,1)或(m+1,﹣1).7.如图,由题意得:点C在直线y=x上,∥如果AB、CD为对角线,AB与CD交于点F,当FC∥直线y=x时,CD最小,易知直线AB为y=x﹣2,∥AF=FB,∥点F坐标为(2,﹣1),∥CF∥直线y=x,设直线CF为y=﹣x+b′,F(2,﹣1)代入得b′=1,∥直线CF为y=﹣x+1,由,解得:,∥点C坐标(,).∥CD=2CF=2×=3.∥如果CD是平行四边形的边,则CD=AB==2>3,∥CD的最小值为3.故答案为:3.8.(1)利用平行四边形的性质:对边平行且相等,得出图1,2,3中顶点C的坐标分别是:(5,2)、(e+c,d),(c+e﹣a,d).故答案为:(5,2)(e+c,d),(c+e﹣a,d).(2)若平行四边形ABCD的顶点A,B,D的坐标分别为(4,1)、(3,4)、(6,4),则顶点C的坐标为(5,7);故答案为:(5,7);(3)如图4中,分别过点A,B,C,D作x轴的垂线,垂足分别为A1,B1,C1,D1,分别过A,D作AE∥BB1于E,DF∥CC1于点F.在平行四边形ABCD中,CD=BA,又∥BB1∥CC1,∥∥EBA+∥ABC+∥BCF=∥ABC+∥BCF+∥FCD=180°.∥∥EBA=∥FCD.在∥BEA∥∥CFD中,,∥∥BEA∥∥CFD(AAS),∥AE=DF=a﹣c,BE=CF=d﹣b.设C(x,y).由e﹣x=a﹣c,得x=e+c﹣a.由y﹣f=d﹣b,得y=f+d﹣b.∥C(e+c﹣a,f+d﹣b),∥m=e+c﹣a,n=f+d﹣b,∥m+a=e+c,n+b=d+f.故答案为:m+a=e+c,n+b=d+f.9.解:(1)∥矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是(6,8),∥OA=6,AB=8,∥OAB=90°,∥OB==10,即线段BO的长是10;(2)设点D的坐标为(0,d),则OD=d,CD=8﹣d,∥BC=6,CD=DE,OB=10,,∥,得d=5,即点D的坐标为(0,5),设折痕所在直线BD的解析式为y=kx+b,∥点D(0,5),点B(6,8)在直线BD上,∥,得,即折痕所在直线BD的解析式是y=0.5x+5;(3)在直线BD上存在点P,使以C、D、M、P为顶点的四边形是平行四边形,点P的坐标为(﹣2,4)或(﹣8,1);理由:∥点C(0,8),点D(0,5),∥OC=8,OD=5,∥CD=3,∥以C、D、M、P为顶点的四边形是平行四边形,点M在直线y=﹣x上,点P在直线BD上,∥CD=MP,CD∥MP,或CD为平行四边形的对角线,当CD=MP,CD∥MP时,设点M的坐标为(m,﹣0.5m),则P的坐标为(m,0.5m+5),则|(0.5m+5)﹣(﹣0.5m)|=3,解得,m1=﹣2,m2=﹣8,当m=﹣2时,点P的坐标为(﹣2,4),当m=﹣8时,点P的坐标为(﹣8,1),当CD为平行四边形的对角线时,则点C和点D中点的坐标为(0,6.5),设点M的坐标为(m,﹣0.5m),则点P的坐标为(﹣m,13+0.5m),∥点P在直线BD上,直线BD的解析式是y=0.5x+5,∥13+0.5m=﹣0.5m+5,得m=﹣8,∥点P的坐标为(8,9),由上可得,点P的坐标为(﹣2,4)、(﹣8,1)或(8,9).10.D11.解:(1)过点A作AM∥CD于M,根据勾股定理,AD=10,AM=BC=8,∥DM==6,∥CD=16;(2)当四边形PBQD为平行四边形时,点P在AB上,点Q在DC上,如图1,由题知:BP=10﹣3t,DQ=2t ∥10﹣3t=2t,解得t=2;(3)在运动过程中,不存在四边形BCQP是矩形,理由如下:∥AB∥CD,∥BCD=90°,∥∥C=90°,若要四边形BCQP是矩形,则当PB=CQ时即10﹣3t=16﹣2t,解得:t=﹣6<0,∥不存在.12.解:(1)∥四边形OACB是平行四边形,∥AC=OB,∥A(1,3)、B(4,0),∥C(5,3);(2)如图(2),设AB所在的直线的解析式为y=kx+b,∥直线AB经过点A(1,3)、B(4,0),∥,∥AB所在直线的解析式为y=﹣4x+4,由于OC所在直线的表达式为y=x,联立方程解得:即M的坐标是(2.5,1.5);(3)存在这样的D、E,使得四边形AOED是矩形.分别过点A、O作AD∥BC于点D,OE∥BC于点E,过E、D分别作x轴的垂线,垂足分别为F、G,∥四边形AOBC是平行四边形,∥AO∥BC,∥AD∥AO,∥四边形AOED是矩形,且与平行四边形AOBC面积相等,∥平行四边形AOBC的面积为12,∥矩形AOED的面积为12,由勾股定理知AO=,∥OE=,EB=,∥EF===1.2,OF===3.6,∥点E的坐标为(3.6,﹣1.2),∥点D的坐标为(4.6,1.8).13.如图,∥A(﹣1,0),C(﹣1,5),∥AC∥x轴,且AC=5﹣0=5,过点D(﹣5,z)作作x轴的垂线,则z的数值就在直线x=﹣5上,;∥A、B、C、D四个点构成的四边形是菱形,∥当DC=DA,z有1个值,当DC=AC,则42+(5﹣z)2=52,z有两个值,当AD=AC,则42+z2=52,则z有两个值,综上所知,符合条件的z的值有5个.故选:D.14.解:(1)对于直线y=﹣x+3,令x=0得到y=3,令y=0,得到x=6,A(6,0)B(0,3).(2)由,解得,∥C(2,2),∥S∥OBC=×3×2=3(3)∥∥M(6﹣t,﹣(6﹣t)+3),N(6﹣t,6﹣t),∥MN=|﹣(6﹣t)+3﹣(6﹣t)|=|t﹣6|,∥OA=3MN,∥6=3|t﹣6|,解得t=或∥如图3中,由题意OC=2,当OC为菱形的边时,可得Q1(﹣2,0),Q2(2,0),Q4(4,0);当OC为菱形的对角线时,Q3(2,0),∥t=(6+2)s或(6﹣2)s或2s或4s时,以O、Q、C、P为顶点的四边形构成菱形.。
平行四边形矩形菱形经典例题(8套)

经典例题(附带详细答案)1.如图,E F 、是平行四边形ABCD 对角线AC 上两点,BE DF ∥,求证:AF CE =.【答案】证明:平行四边形ABCD 中,AD BC ∥,AD BC =,ACB CAD ∴∠=∠.又BE DF ∥,BEC DFA ∴∠=∠,BEC DFA ∴△≌△,∴CE AF =2.如图6,四边形ABCD 中,AB ∥CD ,∠B=∠D ,,求四边形ABCD 的周长.【【答案】20、解法一: ∵∴又∵∴∴∥即得是平行四边形∴∴四边形的周长解法二:连接3 ,6==AB BC AB CD ∥︒=∠+∠180C B B D ∠=∠︒=∠+∠180D C AD BC ABCD 36AB CD BC AD ====,ABCD 183262=⨯+⨯=AC A DCBA DC BD C AB EF∵∴又∵∴≌∴∴四边形的周长解法三:连接∵∴又∵∴∴∥即是平行四边形∴∴四边形的周长3.(在四边形ABCD 中,∠D =60°,∠B 比∠A 大20°,∠C 是∠A 的2倍,求∠A ,∠B ,∠C 的大小.【关键词】多边形的内角和【答案】设x A =∠(度),则20+=∠x B ,x C 2=∠.根据四边形内角和定理得,360602)20(=++++x x x .解得,70=x .∴︒=∠70A ,︒=∠90B ,︒=∠140C .4.(如图,E F ,是四边形ABCD 的对角线AC 上两点,AF CE DF BE DF BE ==,,∥. 求证:(1)AFD CEB △≌△.(2)四边形ABCD 是平行四边形.【关键词】平行四边形的性质,判定【答案】证明:(1)DF BE ∥,DFE BEF ∴∠=∠.180AFD DFE ∠+∠=°,180CEB BEF ∠+∠=°,AFD CEB ∴∠=∠.又A F C E D F ==,,AFD CEB ∴△≌△(SAS).AB CD ∥DCA BAC ∠=∠B D AC CA ∠=∠=,ABC △CDA △36AB CD BC AD ====,ABCD 183262=⨯+⨯=BD AB CD ∥CDB ABD ∠=∠ABC CDA ∠=∠ADB CBD ∠=∠AD BC ABCD 36AB CD BC AD ====,ABCD 183262=⨯+⨯=A BDE F C A DCB(2)由(1)知AFD CEB △≌△,DAC BCA AD BC ∴∠=∠=,,AD BC ∴∥.∴四边形ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形)5.)25.如图13-1,在边长为5的正方形ABCD 中,点E 、F 分别是BC 、DC 边上的点,且AE EF ⊥,2BE =.(1)求EC ∶CF 的值;(2)延长EF 交正方形外角平分线CP P 于点(如图13-2),试判断AE EP 与的大小关系,并说明理由;(3)在图13-2的AB 边上是否存在一点M ,使得四边形DMEP 是平行四边形?若存在,请给予证明;若不存在,请说明理由.【关键词】平行四边形的判定【答案】解:(1)AE EF ⊥2390∴∠+∠=°四边形ABCD 为正方形90B C ∴∠=∠=°1390∴∠+∠=°12∠=∠90DAM ABE DA AB ∠=∠==°,DAM ABE ∴△≌△DM AE ∴=AE EP =DM PE ∴=∴四边形DMEP 是平行四边形.解法②:在AB 边上存在一点M ,使四边形DMEP 是平行四边形证明:在AB 边上取一点M ,使AM BE =,连接ME 、MD 、DP .90AD BA DAM ABE =∠=∠=,°Rt Rt DAM ABE ∴△≌△14DM AE ∴=∠=∠,1590∠+∠=°4590∴∠+∠=°AE DM ∴⊥AE EP ⊥ A D C B E B C E DA F P FDM EP ∴⊥∴四边形DMEP 为平行四边形6.(2009年广州市)如图9,在ΔABC 中,D 、E 、F 分别为边AB 、BC 、CA 的中点。
平行四边形、矩形、菱形、正方形知识点及习题

平行四边形、矩形、菱形、正方形知识点及习题一.正确理解定义(1)定义:两组对边分别平行的四边形是平行四边形.平行四边形的定义揭示了图形的最本质的属性,它既是平行四边形的一条性质,又是一个判定方法.(2)表示方法:用“”表示平行四边形,例如:平行四边形ABCD记作ABCD,读作“平行四边形ABCD”.2.熟练掌握性质平行四边形的有关性质和判定都是从边、角、对角线三个方面的特征进行简述的.(1)角:平行四边形的邻角互补,对角相等;(2)边:平行四边形两组对边分别平行且相等;(3)对角线:平行四边形的对角线互相平分;(4)面积:①S=底高ah;②平行四边形的对角线将四边形分成4=⨯个面积相等的三角形.3.平行四边形的判别方法①定义:两组对边分别平行的四边形是平行四边形②方法1:两组对角分别相等的四边形是平行四边形③方法2:两组对边分别相等的四边形是平行四边形④方法3:对角线互相平分的四边形是平行四边形⑤方法4:一组平行且相等的四边形是平行四边形二、.几种特殊四边形的有关概念(1)矩形:有一个角是直角的平行四边形是矩形,它是研究矩形的基础,它既可以看作是矩形的性质,也可以看作是矩形的判定方法,对于这个定义,要注意把握:①平行四边形;②一个角是直角,两者缺一不可.(2)菱形:有一组邻边相等的平行四边形是菱形,它是研究菱形的基础,它既可以看作是菱形的性质,也可以看作是菱形的判定方法,对于这个定义,要注意把握:①平行四边形;②一组邻边相等,两者缺一不可.(3)正方形:有一组邻边相等且有一个直角的平行四边形叫做正方形,它是最特殊的平行四边形,它既是平行四边形,还是菱形,也是矩形,它兼有这三者的特征,是一种非常完美的图形.2.几种特殊四边形的有关性质(1)矩形:①边:对边平行且相等;②角:对角相等、邻角互补;③对角线:对角线互相平分且相等;④对称性:轴对称图形(对边中点连线所在直线,2条).(2)菱形:①边:四条边都相等;②角:对角相等、邻角互补;③对角线:对角线互相垂直平分且每条对角线平分每组对角;④对称性:轴对称图形(对角线所在直线,2条).(3)正方形:①边:四条边都相等;②角:四角相等;③对角线:对角线互相垂直平分且相等,对角线与边的夹角为450; ④对称性:轴对称图形(4条).3.几种特殊四边形的判定方法(1)矩形的判定:满足下列条件之一的四边形是矩形①有一个角是直角的平行四边形; ②对角线相等的平行四边形; ③四个角都相等(2)菱形的判定:满足下列条件之一的四边形是矩形①有一组邻边相等的平行四边形; ②对角线互相垂直的平行四边形; ③四条边都相等.(3)正方形的判定:满足下列条件之一的四边形是正方形.① 有一组邻边相等 且有一个直角 的平行四边形② 有一组邻边相等 的矩形; ③ 对角线互相垂直 的矩形. ④ 有一个角是直角 的菱形 ⑤ 对角线相等 的菱形;4.几种特殊四边形的常用说理方法与解题思路分析(1)识别矩形的常用方法① 先说明四边形ABCD 为平行四边形,再说明平行四边形ABCD 的任意一个角为直角.② 先说明四边形ABCD 为平行四边形,再说明平行四边形ABCD 的对角线相等.③ 说明四边形ABCD 的三个角是直角.(2)识别菱形的常用方法① 先说明四边形ABCD 为平行四边形,再说明平行四边形ABCD 的任一组邻边相等.② 先说明四边形ABCD 为平行四边形,再说明对角线互相垂直.③ 说明四边形ABCD 的四条相等.(3)识别正方形的常用方法① 先说明四边形ABCD 为平行四边形,再说明平行四边形ABCD 的一个角为直角且有一组邻边相等.② 先说明四边形ABCD 为平行四边形,再说明对角线互相垂直且相等. ③ 先说明四边形ABCD 为矩形,再说明矩形的一组邻边相等.④ 先说明四边形ABCD 为菱形,再说明菱形ABCD 的一个角为直角.5.几种特殊四边形的面积问题① 设矩形ABCD 的两邻边长分别为a,b ,则S 矩形=ab .② 设菱形ABCD 的一边长为a ,高为h ,则S 菱形=ah ;若菱形的两对角线的长分别为a,b ,则S 菱形=12ab . ③ 设正方形ABCD 的一边长为a ,则S 正方形=2a ;若正方形的对角线的长为a ,则S 正方形=212a .特殊四边形练习题1.矩形具有而菱形不一定具有的性质是()A.对边分别相等B.对角分别相等C.对角线互相平分 D.对角线相等2.以下条件不能判别四边形ABCD是矩形的是()A.AB=CD,AD=BC,∠A=90°B.OA=OB=OC=ODC.AB=CD,AB∥CD,AC=BD D.AB=CD,AB∥CD,OA=OC,OB=OD3.顺次连接四边形ABCD各边中点所成的四边形为菱形,那么四边形ABCD的对角线AC和BD只需满足的条件是()A.相等B.互相垂直C.相等且互相垂直 D.相等且互相平分4.已知菱形的两条对角线长分别是6cm和8cm,则菱形的边长是()A.12cm B.10cm C.7cm D.5cm5.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为()A.16 B.15 C.14 D.136.如图,E,G,F,H分别是矩形ABCD四条边上的点,EF⊥GH,若AB=2,BC=3,则EF:GH=()A.2:3 B.3:2 C.4:9 D.无法确定7.如图:在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是.8.平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF;②△EFG≌△GBE;③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是.9. 如图,在矩形ABCD(AB<AD)中,将△ABE沿AE对折,使AB边落在对角线AC上,点B的对应点为F,同时将△CEG沿EG对折,使CE边落在EF所在直线上,点C的对应点为H.(1)证明:AF∥HG(图(1));(2)证明:△AEF∽△EGH(图(1));(3)如果点C的对应点H恰好落在边AD上(图(2)).求此时∠BAC的大小.10.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.(1)证明:四边形ADCE为菱形.(2)BC=6,AB=10,求菱形ADCE的面积.11.如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE 于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.(1)求证:四边形AECF为矩形;(2)试猜想MN与BC的关系,并证明你的猜想;(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.12.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)求证:BD=DF;(2)求证:四边形BDFG为菱形;(3)若AG=13,CF=6,求四边形BDFG的周长.。
平行四边形、矩形、菱形,正方形练习题

平行四边形、矩形、菱形、正方形1.:如图,在▱ABCD中,点E、F是对角线AC上的两点,且AE=CF.求证:BF∥DE.2.如图,平行四边形ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.3.如图,四边形ABCD是平行四边形,E、F分别是BC、AD上的点,∠1=∠2.求证:AF=CE.4.:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:〔1〕AE=AB;〔2〕如果BM平分∠ABC,求证:BM⊥CE.5.如图,在▱ABCD中,点E、F在BD上,且BE=AB,DF=CD.求证:四边形AECF是平行四边形.6.在▱ABCD中,E,F分别是AB,DC上的点,且AE=CF,连接DE,BF,AF.〔1〕求证:四边形DEBF是平行四边形;〔2〕假设AF平分∠DAB,AE=3,DE=4,BE=5,求AF的长.7.如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,〔1〕求证:AE=CE;〔2〕求证:四边形ABDF是平行四边形;〔3〕假设AB=2,AF=4,∠F=30°,那么四边形ABCF的面积为.8.如图,在▱ABCD中,E,F分别是AC上两点,BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF为平行四边形.9.:如图,点E、F在线段BD上,AB=CD,∠B=∠D,BF=DE.求证:〔1〕AE=CF;〔2〕AF∥CE.10.如下列图,▱ABCD中,E,F分别是AB、CD上的点,AE=CF,M、N分别是DE、BF的中点.〔1〕求证:四边形ENFM是平行四边形.〔2〕假设∠ABC=2∠A,求∠A的度数.11.在▱ABCD中,点E,F分别在AD,BC上,AE=CF,连接EF,BD.〔1〕求证:四边形EBFD是平行四边形;〔2〕假设∠C+∠ABE=90°,求证:BD=EF.12.如图,在▱ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.〔1〕求证:△ABE≌△CDF.〔2〕求证:四边形AECF是平行四边形.13.如图,在△NMB中,BM=6,点A,C,D分别在边MB、BN、MN上,DA∥NB,DC∥MB,∠NDC=∠MDA.求四边形ABCD的周长.14.在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.〔1〕AE=,EF=〔2〕假设G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.〔3〕在〔2〕条件下,当t为何值时,四边形EGFH为矩形.15.如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.〔1〕求证:四边形BFDE是矩形;〔2〕∠DAB=60°,AF是∠DAB的平分线,假设AD=3,求DC的长度.16.如图,▱ABCD中,O是AB的中点,CO=DO.〔1〕求证:▱ABCD是矩形.〔2〕假设AD=3,∠COD=60°,求▱ABCD的面积.17.如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD〔1〕求证:四边形AEBD是矩形;〔2〕连接CE交AB于点F,假设BE=2,AE=2,求EF的长.18.如图,在平行四边形ABCD中,对角线AC、BD交于点O,AC⊥BC,AC=2,BC=3.点E 是BC延长线上一点,且CE=3,连结DE.〔1〕求证:四边形ACED为矩形.〔2〕连结OE,求OE的长.19.如图,▱ABCD中,点E在BC延长线上,EC=BC,连接DE,AC,AC⊥AD于点A.〔1〕求证:四边形ACED是矩形;〔2〕连接BD,交AC于点F.假设AC=2AD,猜想∠E与∠BDE的数量关系,并证明你的猜想.20.如图,在△ABC中,BD平分∠ABC交AC于D,作DE∥BC交AB于点E,作DF∥AB交BC于点F.〔1〕求证:四边形BEDF是菱形;〔2〕假设∠BDE=15°,∠C=45°,CD =,求DE的长.21.如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD于E,F,G,连接DE,DF.〔1〕求证:四边形BEDF是菱形;〔2〕假设∠BDE=15°,∠C=45°,DE=2,求CF的长.22.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC 交BE的延长线于点F.〔1〕求证:四边形ADCF是菱形;〔2〕假设AC=12,AB=16,求菱形ADCF的面积.23.如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.〔1〕求证:四边形ABCD是菱形;〔2〕假设AB=2,BD=4,求OE的长.24.如图,AC是▱ABCD的对角线,∠BAC=∠DAC.〔1〕求证:四边形ABCD是菱形;〔2〕假设AB=2,AC=2,求四边形ABCD的面积.25.同学丰用一长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF〔如图〕.〔1〕证明:四边形AECF是菱形;〔2〕求菱形AECF的面积.26.如图,EF是平行四边形ABCD的对角线BD的垂直平分线,EF与边AD、BC分别交于点E、F.〔1〕求证:四边形BFDE是菱形;〔2〕假设ED=5,BD=8,求菱形BFDE的面积.27.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.〔1〕求证:四边形ABCD是菱形;〔2〕假设∠ADB=30°,BD=12,求AD的长.28.如图,在▱ABCD中,BC=2AB,点E、F分别是BC、AD的中点,AE、BF交于点O,连接EF,OC.〔1〕求证:四边形ABEF是菱形;〔2〕假设AB=4,∠ABC=60°,求OC的长.29.:如图,菱形ABCD的对角线AC与BD相交于点O,假设∠CAD=∠DBC.〔1〕求证:四边形ABCD是正方形.〔2〕E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.30.:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.〔1〕求证:四边形EFCD是正方形;〔2〕假设BE=1,ED=2,求BD的长.31.如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作CE∥BD,DE∥AC.求证:四边形OCED是正方形.32.如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,假设正方形ABCD的周长是40cm.〔1〕求证:四边形BFEG是矩形;〔2〕求四边形EFBG的周长;〔3〕当AF的长为多少时,四边形BFEG是正方形.33.如图,正方形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是正方形.34.E、F、M、N分别是正方形ABCD四条边上的点,AE=BF=CM=DN,四边形EFMN是什么图形.证明你的结论.35.如图,点E、F分别是矩形ABCD的边AB、CD上的一点,且DF=BE.求证:四边形AECF是平行四边形.36.如图,矩形ABCD中,对角线AC、BD交于点O,以AD、OD为邻边作平行四边形ADOE,连接BE.求证:四边形AOBE为菱形.37.如图,在矩形ABCD中,点O为对角线AC的中点,过点O作EF⊥AC交BC于点E,交AD 于点F,连接AE,CF.〔1〕求证:四边形AECF是菱形;〔2〕连接OB,假设AB=8,AF=10,求OB的长.38.如图,在菱形ABCD中,∠ABC=60°,对角线AC=8,求菱形ABCD的周长和面积.39.如图,在菱形ABCD中,过点B作BE⊥AD于E,过点B作BF⊥CD于F,求证:AE=CF.40.如图,菱形ABCD的对角线AC和BD交于点O,AB=10,∠ABC=60°,求AC和BD的长.41.如图,菱形ABCD两条对角线BD与AC的长之比为3:4,周长为40cm,求菱形的高及面积.42.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,〔1〕求证:∠DHO=∠DCO.〔2〕假设OC=4,BD=6,求菱形ABCD的周长和面积.43.如图,菱形ABCD中,对角线AC、BD相交于点O,点E是AB的中点,AC=8cm,BD=6cm,〔1〕求菱形ABCD的面积.〔2〕求OE的长度.44.在菱形ABCD中,E是AB边的中点,连接DE,DE⊥AB,对角线AC、BD交于点H.〔1〕求∠ABC的度数;〔2〕如果菱形的对角线AC=2,求菱形的面积.45.如图,在正方形ABCD中,点E,F在对角线BD上,AE∥CF,连接AF,CE.〔1〕求证:△ABE≌△CDF;〔2〕试判断四边形AECF的形状,并说明理由.46.如图,小方将一个正方形纸片剪去一个宽为4cm的长方形〔记作A〕后,再将剩下的长方形纸片剪去一个宽为5cm的长方形〔记作B〕.〔1〕假设A与B的面积均为Scm2,求S的值.〔2〕假设A的周长是B的周长的倍,求这个正方形的边长.47.:如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.求证:四边形AECF是菱形48.如图,正方形ABCD中,点P,Q分别为AD,CD边上的点,且DQ=CP,连接BQ,AP.求证:BQ=AP.49.如图,正方形CDEF的面积为169cm2,且AC⊥AF,AB=3cm,BC=4cm,AF=12cm,试判断△ABC的形状,并说明你的理由.50.如图,正方形ABCD中,AB=AD,G为BC边上一点,BE⊥AG,于E,DF⊥AG于F,连接DE.〔1〕求证:△ABE≌△DAF;〔2〕假设AF=1,EF=4,求四边形ABED的面积.。
2020年中考数学必考34个考点专题19:平行四边形(含答案解析)

专题19 平行四边形专题知识回顾1.平行四边形定义:有两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“□ABCD”表示,如平行四边形ABCD记作“□ABCD”,读作“平行四边形ABCD”。
2.平行四边形的性质:(1)平行四边形的对边平行且相等;(2)平行四边形的对角相等;(3)平行四边形的对角线互相平分。
3.平行四边形的判定:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)对角线互相平分的四边形是平行四边形;(5)两组对角分别相等的四边形是平行四边形。
4.平行四边形的面积:S平行四边形=底边长×高=ah专题典型题考法及解析【例题1】(2019▪广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是()A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF【答案】B.【解析】利用三角形中位线定理得到DE AC,结合平行四边形的判定定理进行选择.∵在△ABC中,D,E分别是AB,BC的中点,∴DE是△ABC的中位线,∴DE A C.A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.【例题2】(2018湖北黄石)如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.(1)判断四边形ACGD的形状,并说明理由.(2)求证:BE=CD,BE⊥CD.【答案】看解析。
专题19平行四边形、矩形、菱形--拔高题

专题19平行四边形、矩形、菱形阅读与思考平行四边形、矩形、 菱形的性质定理与判定定理是从对边、对角、对角线三个方面探讨的,矩形、菱形都是特殊的平行四边形, 矩形的特殊性由一个直角所体现, 菱形的特殊性是由邻边相等来体现,因此它们除兼有平行四边形的一般性质外,还有特有的性质;反过来, 判定一个四边形为矩形或菱形,也就需要更多的条件连对角线后平行四边形、矩形、菱形就与特殊三角形联系在一起,所以讨论平行四边形、矩形、菱形相关问题时,常用到特殊三角形性质、全等三角形法;另一方面,又要善于在四 边形的背景下思考问题, 运用平行四边形、矩形、 菱形的丰富性质为解题服务,常常是判定 定理与性质定理的综合运用 .熟悉以下基本图形:例题与求解【例I 】如图,矩形 ABCD 的对角线相交于 O , AE 平分/ BAD ,交BC 于E ,/ CAE = 15 ° 那么/ BOE = _________ .(祖冲之杯”邀请赛试题)解题思路:从发现矩形内含的特殊三角形入手 【例2】下面有四个命题:① 一组对边相等且一组对角相等的四边形是平行四边形;② 一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;③ 一组对角相等且这一组对角的顶点所连结的对角线平分另一条对角线的四边形是平 行四边形;④ 一组对角相等且这一组对角的顶点所连结的对角线被另一条对角线平分的四边形是 平行四边形;其中,正确的命题的个数是( )A.1B. 2C. 3D.4(全国初中数学联赛试题)S 4S 2S iS 3O解题思路:从四边形边、角、对角线三类元素任意选取两类,任意组合就产生许多判定 平行四边形的命题,关键在于对假命题能突破正规的、标准位置的图形构造反例否定【例3】如图,菱形ABCD 的边长为2,BD = 2, E , F 分别是边AD , CD 上的两个动 点且满足AE+CF = 2.(1) 判断ABEF 的形状,并说明理由; (2) 设ABEF 的面积为S,求S 的取值范围(烟台中考试题)解题思路:对于(1)由数量关系发现图形特征;对于(【例4】如图,设P 为等腰直角三角形 ACB 斜边AB 上任意一点,PE 丄AC 于点E , PF 丄BC 于点F , PG 丄EF 于点G ,延长GP 并在春延长线上取一点 D ,使得PD = PC. 求证:BC 丄 BD , BC = BD.(全国初中数学联赛试题)解题思路:只需证明A CPBDPB ,关键是利用特殊三角形、特殊四边形的性质【例5】在口ABCD 中,/ BAD 的平分线交直线 BC 于点E ,交直线DC 的延长线于点 F.2),只需求出BE 的取值范围DB(北京市中考试题)解题思路:对于(1),由角平分线加平行线的条件可推出图中有 3个等腰三角形; 对于(2),用测量的方法可得/ BDG=45°进而想到等腰直角三角形,连 CG , BD ,只需证明ABGC ◎△ DGF ,这对解决(3),有不同的解题思路• 对于(3)【例6】如图,△ABC 中,/ C = 90°点M 在BC 上,且BM = AC ,点N 在AC 上,且AN = MC , AM 与BN 相交于点 P. 求证:/ BPM = 45°.解题思路:条件给出的是线段的等量关系,求证的却是角度等式, 由于条件中有直角和相等的线段,因此,可想到等腰直角三角形,解题的关键是平移 AN 或AC ,即作ME 丄AN ,ME = AN ,构造平行四边形•能力训练A 级1.如图,口 ABCD 中, BE 丄 CD , BF 丄 AD ,垂足分别为 E 、F ,若 CE = 2, DF = 1,/ EBF = 60 °,贝U □ ABCD 的面积为 _____ .(1) (2) (3) 的度数•在图 若/ 若/ 1中证明CE = CF ;ABC = 90° G 是 EF ABC = 120° FG // CE , FG = CE ,分别连结 DB , DG (如图 3),求/ BDG的中点 (如图2),直接写出/BDG 的度数;FCFNC(浙江省竞赛试题)(浙江省中考试题)在 Rt △ABC 中,/ B = 90 ° / BAC = 78 ° 过 C 作 CF // AB ,连结 AF 与 BC(希望杯”竞赛试题)4. 如图,在菱形 ABCD 中,/ B =Z EAF = 60° / BAE = 20。
特殊的平行四边形:矩形、菱形、正方形(单元知识点及典型题)

特殊的平行四边形:矩形、菱形、正方形【知识要点】一. 教学内容:几种特殊的平行四边形:矩形、菱形、正方形[教学目标]1. 理解矩形、菱形的定义与性质。
2. 掌握矩形、菱形的判定方法。
二. 教学重难点:1. 矩形、菱形性质的综合应用。
特别是菱形性质和直角三角形的知识的综合应用。
2. 矩形、菱形的判定方法的综合应用。
三. 知识要点: 1. 矩形(1)矩形的概念有一个角是直角的平行四边形叫矩形。
(2)矩形的特殊性质 ①矩形的对角线相等 ②矩形四个角都是直角 (3)矩形性质的应用①矩形的一条对角线将矩形分成2个全等的直角三角形; ②矩形的2条对角线将矩形分成4个等腰三角形;③有关矩形的问题往往可以化为直角三角形或等腰三角形的问题来解决; ④矩形的面积计算公式: 宽长矩形⨯=S(4)矩形的判定条件①有三个角是直角的四边形是矩形 ②对角线相等的平行四边形是矩形 注意:1)在判定四边形是矩形的条件中,平行四边形的概念是最基本的条件,其他的判定条件都是以它为基础的。
2)四边形只要有3个角是直角,那么根据多边形内角和性质,第四个角也一定是直角。
(在判定四边形是矩形的条件中,给出“有3个角是直角”的条件,是因为数学结论的表述中一般不给出多余条件。
)3)将两个判定条件比较,后者的条件中,除了“有3个角是直角”的条件外,只要求是“四边形”,而前者的条件却包括“平行四边形”和“两条对角线相等”两个方面。
4)矩形的判定与性质的区别【名师提醒】:1、矩形是_____对称图形,对称中心______。
又是______对称图形,对称轴有_____条。
2、矩形被它的对角线分成四个面积相等的_____三角形,其中相对的三角形全等。
3、矩形中常见题目是对角线相交成60°或120°角时,利用直角三角形、等边三角形 等知识解决问题 2. 菱形(1)菱形的概念有一组邻边相等的平行四边形叫菱形。
(2)菱形的特殊性质 ①菱形的四条边都相等②菱形的对角线相互垂直,且每一条对角线平分一组对角 (3)菱形性质的应用由于菱形的对角线互相垂直平分,菱形的2条对角线就将菱形分成了四个全等的直角三角形,结合图形向学生介绍菱形的一个面积计算公式。
平行四边形、矩形、菱形、正方形提高题
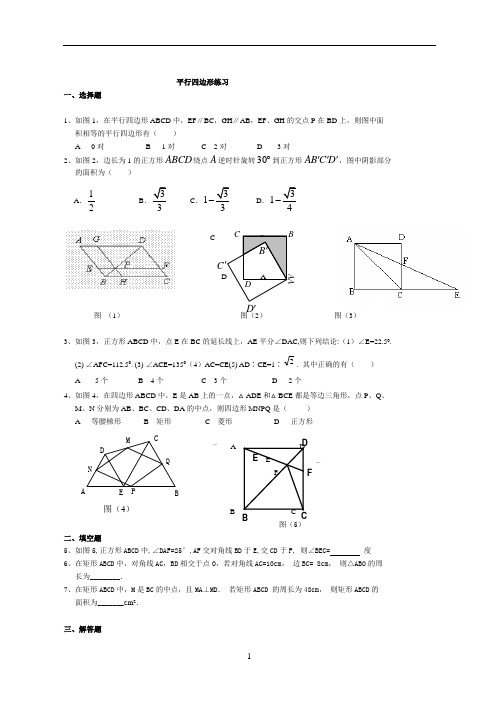
平行四边形练习 一、选择题1、如图1,在平行四边形ABCD 中,EF ∥BC ,GH ∥AB ,EF 、GH 的交点P 在BD 上,则图中面 积相等的平行四边形有( )A 0对B 1对C 2对D 3对 2、如图2,边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D ''',图中阴影部分的面积为( )A .12B .33C .313-D .314-CBD A图 (1) 图(2) 图(3)3、如图3,正方形ABCD 中,点E 在BC 的延长线上,AE 平分∠DAC,则下列结论:(1)∠E=22.50. (2) ∠AFC=112.50. (3) ∠ACE=1350(4)AC=CE(5) AD ∶CE=1∶2. 其中正确的有( ) A 5个 B 4个 C 3个 D 2个4、如图4,在四边形ABCD 中,E 是AB 上的一点,△ADE 和△BCE 都是等边三角形,点P 、Q 、 M 、N 分别为AB 、BC 、CD 、DA 的中点,则四边形MNPQ 是( ) A 等腰梯形 B 矩形 C 菱形 D 正方形A DEFB C图(5)二、填空题5、如图5,正方形ABCD 中,∠DAF=25°,AF 交对角线BD 于E,交CD 于F, 则∠BEC= 度6、在矩形ABCD 中,对角线AC ,BD 相交于点O ,若对角线AC=10cm ,•边BC=•8cm ,•则△ABO 的周 长为________.7、在矩形ABCD 中,M 是BC 的中点,且MA ⊥MD .•若矩形ABCD•的周长为48cm ,•则矩形ABCD 的 面积为_______c m 2.三、解答题C BB '__D C 'D 'DAAQ E PMN DCBA 图(4)_ E _ F_ B_ C8、已知,如图,矩形ABCD 的对角线AC ,BD 相交于点O ,E ,F 分别是OA ,OB 的中点. (1)求证:△ADE ≌△BCF ;(2)若AD=4cm ,AB=8cm ,求OF 的长.10、如图,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF =BE . ⑴求证:CE =CF ;⑵在图1中,若G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗?为什么? ⑶运用⑴⑵解答中所积累的经验和知识,完成下题:如图2,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B =90°,AB =BC =6,E 是AB 上一点, 且∠DCE =45°,BE =2,求DE 的长.6.如图1,在△ABC 中,AB=BC ,P 为AB 边上一点,连接CP ,以PA 、PC 为邻边作□APCD ,AC 与PD 相交于点E ,已知∠ABC=∠AEP=α(0°<α<90°). (1)求证:∠EAP=∠EPA;(2)□APCD 是否为矩形?请说明理由;(3)如图2,F 为BC 中点,连接FP ,将∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN(点M 、N 分别是∠MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系,并证明你的结论.图1ABDCE P 图2ABDCEPM NFB CA G D FEB CA DE图1图2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例I 】如图,矩形
ABCD 的对角线相交于
O , AE 平分/BAD ,交 BC 于 E,Z CAE =
专题19平行四边形、矩形、菱形
阅读与思考
平行四边形、矩形、 菱形的性质定理与判定定理是从对边、对角、 对角线三个方面探讨
的,矩形、菱形都是特殊的平行四边形, 矩形的特殊性由一个直角所体现,
菱形的特殊性是 由邻边相等来体现,因此它们除兼有平行四边形的一般性质外,还有特有的性质;反过来, 判定一个四边形为矩形或菱形,也就需要更多的条件
连对角线后平行四边形、矩形、菱形就与特殊三角形联系在一起, 所以讨论平行四边形、 矩形、菱形相关问题时,常用到特殊三角形性质、全等三角形法;另一方面,又要善于在四 边形的背景下思考问题, 运用平行四边形、矩形、 菱形的丰富性质为解题服务,常常是判定 定理与性质定理的综合运用 .
熟悉以下基本图形:
例题与求解
15 ° 那么/BOE = _
__________
D
B E
(“祖冲之杯”邀请赛试题)解题思路:从发现矩形内含的特殊三角形入手.
【例2】下面有四个命题:
①一组对边相等且一组对角相等的四边形是平行四边形;
②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;
③一组对角相等且这一组对角的顶点所连结的对角线平分另一条对角线的四边形是平行四边形;
④一组对角相等且这一组对角的顶点所连结的对角线被另一条对角线平分的四边形是平行四边形;
其中,正确的命题的个数是()
A.1
B. 2
C. 3
D.4
(全国初中数学联赛试题)
解题思路:从四边形边、角、对角线三类元素任意选取两类,任意组合就产生许多判定平行四边形的命题,关键在于对假命题能突破正规的、标准位置的图形构造反例否定.
【例3】如图,菱形ABCD的边长为2 , BD = 2 , E, F分别是边AD , CD上的两个动
点且满足AE+CF= 2.
(1)判断A BEF的形状,并说明理由;
(2)设ABEF的面积为S,求S的取值范围.
B
D
(烟台中考试题)
解题思路:对于(1)由数量关系发现图形特征;对于( 2),只需求出BE 的取值范围
【例4】如图,设P 为等腰直角三角形 ACB 斜边AB 上任意一点,PE 丄AC 于点E , PF 丄BC 于点F , PG 丄EF 于点G ,延长GP 并在春延长线上取一点 D ,使得PD = PC .
求证:BC 丄 BD , BC = BD .
(全国初中数学联赛试题)
解题思路:只需证明△CPBB/DPB ,关键是利用特殊三角形、特殊四边形的性质
【例5】在CABCD 中,/BAD 的平分线交直线 BC 于点E ,交直线DC 的延长线于点
F.
度数.
(1) (3) 在图1中证明
若
/ABC = CE = CF ;
,G 是EF 的中点 (如图2 ),直接写出/ BDG 的度数;
若/ABC = 120 ° FG//CE , FG = CE ,分别连结 DB , DG (如图 3),求/ BDG 的
(北京市中考试
题)
解题思路:对于(1),由角平分线加平行线的条件可推出图中有
3个等腰三角形; 对于(2),用测量的方法可得/ BDG =45 °进而想到等腰直角三角形,连 CG, BD ,只需
证明ABGC^/DGF ,这对解决(3 ),有不同的解题思路.
对于(3) 【例6】如图,A ABC 中,/ C = 90 °点M 在BC 上,且BM = AC ,点N 在AC 上, 且AN = MC , AM 与BN 相交于点 P .
求证:/ BPM = 45 °
F
A D C
B
图2 E
G F F
1.如图,
□ABCD 中,BE 丄CD , BF 丄AD ,垂足分别为 E 、F ,若CE = 2 , DF = 1,Z EBF = 60 ° 贝U □XBCD 的面积为 2.如图, □ABCD 的对角线相交于点 O ,且AD £D ,过点O 作OM 丄AC ,交AD 于 (浙江省竞赛试题) 解题思路:条件给出的是线段的等量关系, 求证的却是角度等式, 由于条件中有直角和 相等的线段,因此,可想到等腰直角三角形, 解题的关键是平移 AN 或AC ,即作ME 丄AN , ME = AN ,构造平行四边形• 能力训练
点M ,若△CDM 周长为a ,那么CABCD 的周长为
第2题
C.对角线互相垂直的四边形
D.对角线相等的四边形 (浙江省中考试题) 3.如图,在 Rt △ABC 中,/B = 90 ° ZBAC = 78 ° 过 C 作 CF//AB ,连结 AF 与 BC 相 交于G ,若GF = 2AC ,则/BAG 的大小是 ______________ . (希望杯”竞赛试题) 4.如图,在菱形ABCD 中,ZB =/EAF = 60 ° ZBAE = 20。
,则/CEF 的大小是 _________________
(希望杯”邀请赛试题) 5.四边形的四条边长分别是 a , b , c , d ,其中a , c 为对边,且满足 a 2 b 2 c 2 d 2 2ab 2cd ,则这个四边形一定是( ) A •两组角分别相等的四边形 B.平行四边形
A
6.现有以下四个命题:
①对角线相等的四边形是矩形;②对角线互相垂直的四边形是菱形;③有一个角为直角且对角线互相平分的四边形为矩形;④菱形的对角线的平方和等于边长的平方的4倍.
其中,正确的命题有()
A.①②
B.③④
C.③
D.①②③④
7.如图,在矩形ABCD中,AB = 1 , AD = , 3 , AF平分/DAB,过点C作CE丄BD
于E,延长AF , EC交于点H,下列结论中:① AF= FH;②BO = BF;③CA = CH :④BE
=3ED.正确的是()
A.②③
B.③④
C.①②④
D.②③④
(齐齐哈尔中考试题)
8.如图,矩形ABCD的长为a,宽为b,如果S $ 丄(S3 S4),则S4 =(
)
2
3 A. —
ab B.3ab C. -ab D.-ab
8 4 3 2
9.已知四边形ABCD,现有条件:① AB//DC;②AB= DC;③AD IIBC:④AD = BC;
⑤上A =Z C;®Z B=Z D.从中取两个条件加以组合,能推出四边形ABCD是平行四边形的
有哪几种情形?请具体写出这些组合.
(江苏省竞赛试题)
10.如图,△ABC为等边三角形,D、F分别是BC、AB上的点,且CD = BF,以AD 为边作等边△ADE.
(1)求证:Z\ACD 也/CBF ;
(2)当D在线段BC上何处时,四边形CDEF为平行四边形,且/ DEF= 30 °证明你
的结论.
(江苏省南通市中考试题)
11.如图,在Rt A ABC 中,AB = AC, ZA= 90。
,点D 为BC 上任一点,DF丄AC 于F,
DE丄AC于E, M为BC中点,试判断AMEF是什么形状的三角形,并证明你的结论
C
E
12.如图,△ABC 中,AB = 3 , AC = 4 , BC = 5 , A ABD , A ACE , △BCF 都是等边三 角形,求四边形 AEFD 的面积.
(山东省竞赛试题)
1.如图,已知 ABCD 是平行四边形,E 在AC 上,AE = 2EC , F 在AB 上,BF = 2AF , 如果ABEF 的面积为2 cm 2
,则/BCD 的面积是 _______________ . 第1题
(希望杯”竞赛试题)
2.如图,已知 P 为矩形 ABCD 内一点,PA = 3 , PD = 4 , PC = 5 ,贝U PB= ______________
第2题
3.如图,在矩形ABCD中,AB = 6cm , BC= 8cm,现将矩形折叠,使B点与D点重
合,则折痕EF长为__________
(武汉市竞赛试题)
4.如图,在矩形ABCD中,AB = 8, BC= 4,将矩形沿AC折叠,使点D落在点D处,
CD交AB于点F,则重叠部分△AFC的面积为_______________ .
第4题
(山东省竞赛试题)
5.如图,在矩形ABCD中,已知AD = 12 , AB = 5 , P是AD边上任意一点,PE丄BD
于E, PF丄AC于F,那么PE+ PF的值为_____________。
