二年级学而思巧算8.15
二年级学而思秋季数学超常班讲义

一笔画游戏第七讲下列图形能一笔画成吗?如果可以,在图形下面的方框里画上√,如果不可以,在图形下面的方框里画上╳.【例题分析】在这些图形中可以一笔画出的是:①、②、④;不可以一笔画出的是:③.一个图形是否能一笔画成跟这些点有什么关系?⑴从一点出发的线的条数是偶数(双数),这点称为偶点(双数点).⑵从一点出发的线的条数是奇数(单数),这点称为奇点(单数点).观察此题的每个图:①有2个奇点,能一笔画成;②有0个奇点,能一笔画成;③有4个奇点,不能一笔画成;④有2个奇点,能一笔画成.最后总结出:有0个或2个奇点的连通图能够一笔画成,否则不能一笔画成.下列图形能一笔画成吗?为什么?如果可以,在图形下面的方框里画上√,如果不可以,在图形下面的方框里画上╳.【例题分析】①、②、③可以,④不可以.①有2个奇点,②有0个奇点,③有2个奇点,所以①、②、③可以一笔画.④有4个奇点,所以④不能一笔画.下列图形能一笔画成吗?如果可以,在图形下面的方框里画上√,如果不可以,在图形下面的方框里画上╳.【例题分析】①③⑤可以;②④不可以.①有0个奇点;③有2个奇点;⑤有0个奇点;所以①③⑤可以一笔画.②有4个奇点;④有6个奇点;所以②④不能一笔画.【例题分析】⑴ 图①中有4个点是奇点,所以不能一笔画成,要想使这个图形能一笔画成,可以添加一条线段,使这个图形的奇点变成2个.如下图(答案不唯一):⑵图②因为有4个点是奇点,所以不能一笔画成,要想使这个图形能一笔画成,可以添加一条线段,使这个图形的奇点变成2个.如下图(答案不唯一):⑶图③中有4个点是奇点,所以不能一笔画成,要想使这个图形一笔画成,可以添加一条线段,使这个图形的奇点变成2个.如下图:下面的图形都不能一笔画成,请你分别在各图中添上一条线段,使它能一笔画成.【例题分析】上图一共有6个奇点,只添一条线段无法变成2个奇点,至少需要添上2条线段.如下图(答案不唯一):下面的图形都不能一笔画成,请你在各个图中分别去掉一条线,使它能一笔画成,在去掉的线上打╳.下面的图形不能一笔画成,至少添上几条线段才能使它一笔画成?试着添一添.【例题分析】⑴图①中有4个点是奇点,所以不能一笔画成,要想使这个图形能一笔画成,就要使这个图形的奇点变成2个.如下图(答案不唯一):⑵图②和图①相似,因为有4个点是奇点,所以不能一笔画成,要想使这个图形能一笔画成,就要使这个图形的奇点变成2个.如下图(答案不唯一):⑶图③中有4个点是奇点,所以不能一笔画成,要想使这个图形一笔画成,就要使这个图形的奇点变成2个.如下图(答案不唯一):下面的图形不能一笔画成,请你去掉一条线,使它能一笔画成,在去掉的线上打╳.【例题分析】图中有4个点是奇点,所以不能一笔画成,要想使这个图形能一笔画成,就要使这个图形的奇点变成2个.如下图(答案不唯一):( )→( )→( )→( )→( )→( )→( )→( )→( )→( )→( )→( )→( )→( )【例题分析】出入口应设在A 、C 两个奇点处.A →B →C →I →A →H →G →I →E →G →F →E →D →C (路线不唯一). 本题实际上是这个图以哪两点为起点和终点一笔画出的问题,观察上图可以发现仅有两个奇点: A 点与C 点.因此,出入口应设在A 、C 两个奇点处.下图是一个小区街道的平面图.要不重复地走遍每条街道,出入口应设在哪里?请你再设计一条不重复走遍每条街道的行走路线,用字母和箭头表示出来.下图是乡间的小河,上面建有九座桥,你能从其中一个村子出发一次不重复地走遍所有的桥吗? (每座桥最多只准走一次,陆地上可以重复地走)【例题分析】可以,丁→丙→丁→甲→丁→乙→丙→乙→甲→乙.(路线不唯一)首先将实物图转化成点线图,所有的村庄都转化成点,所有的桥都转化成线(如下图),图中有2个奇点,所以可以一笔画,也就存在一条路线,能够不重复地走遍所有的桥.我国著名数学家陈景润所著《数学趣谈》一书中,有这样一道题:在法国的首都巴黎有一条河,河中有两个小岛,那里的人们建了15座桥把两个小岛和河岸连接起来,如下图所示.那么,从任一岸出发,不重复地走遍所有的桥到达另一岸,能做到吗?【例题分析】能.将实物图转化成点线图,如下图,图中有2个奇点,可以一笔画,也就是说可以从任一岸出发,不重复地走遍所有的桥到达另一岸.如图是一个超市的平面图,超市共有A、B、C、D、E、F六个门,简乐想一次走遍所有通道而又不走重复路线,请你帮他设计一种进出方法.【例题分析】把每一条通道看作是边,通道的交点看作是点(每个门处即为一个点),可得下图,这样问题就转化为能否从某点出发将图一笔画的问题.观察可知,如上右图中只有两个奇点(点C和点D),根据一笔画原理可得:将点C和点D分别作为起点和终点,可将右图一笔画出.即简乐从C门(或D门)进超市,一次走遍所有通道后从D门(或C门)出超市,其行进路线为:C→D→E→O→C→B→E→F→A→B→O→D(路线不唯一).下图是某展览厅的平面图,它由五个展室组成,任意两个展室之间都有门相通,整个展览厅还有一个入口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?【例题分析】把每个展室看作一个点,整个展厅的外部也看作一个点,两室之间有门相通,可以看作两点之间有线相连.这样,展厅的平面图就转化成图②,一个实际问题也就转化为这个图能否一笔画成的问题了,即能否从A出发,一笔画完此图,最后再回到A.图②中,所有的点都是偶点,因此,一定可以以A作为起点和终点而一笔画完此图.即游人可以从入口进,一次不重复地穿过所有的门,最后从出口出来.下面仅给出一种参观路线:A→E→B→C→E→F→C→D→F→A.。
【新】沪教版二年级数学下册《巧算》优质公开课课件 (2).ppt

(√ ) (× ) (√ )
讨论:凑成整百数的两个三位数有什么 特点?
探究二 例2:853-498-253
探究二 例2:853-498-253
=853-253-498 =600-498
=102
探究二 例2:853-498-253
=853-253-498
=600-498
=102
为什么要先算“853253”?
=278+(374+226) =278+600 =578
183+99+117
554-217-83 376-199-176
278+374+226
=278+(374+226) =278+600 =578
183+99+117
554-217-83
=554-(217+83) =554-300 =154
376-199-176
=700+243 =943
478+243+222 =(478+222)+243
=700+243 =943
(1)478和222为什么先加?
478+243+222 =(478+222)+243
=700+243 =943
(1)478和222为什么先加?
(2)这两个数中间还夹着一个243, 怎么办?
478+243+222 =(478+222)+243
=389+400
可以巧算吗?那两个数 能凑成整百数?
探究一 探究二
探究一
例1:389+163+237 =389+(163+237)
【新】沪教版二年级数学下册《巧算》优质公开课课件 (2).ppt

237元
389元
163元
探究一
例1:389+163+237
探究一
例1:389+163+237
可以巧算吗?那两个数 能凑成整百数?
探究一 探究二
探究一
例1:389+163+237
可以巧算吗?那两个数
=389+(163+237) 能凑成整百数?
探究一 探究二
探究一
例1:389+163+237 =389+(163+237)
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
凑整百数
判断:能不能巧算
(1)358+227+142 (2)216+253+129 (3)131+235+165
(
)
(
)
(
)
判断:能不能巧算
(1)358+227+142 (2)216+253+129 (3)131+235+165
(√ )
(
)
(
二年级《速算与巧算》奥数教案

(二年级)备课教员:第十五讲速算与巧算一、教学目标:知识目标1. 通过研究算式中的数字特点找到巧算方法。
2. 知道计算中基本的巧算方法,能熟练运用巧算的方法计算。
3.知道加括号和去括号与运算符号之间的变化关系。
能力目标1. 从解决问题的过程中获得成功的体验,树立起学习数学的信心。
2. 一个数可以进行拆分后凑整计算,锻炼学生的数学分组拆分的数学思维。
情感目标1. 培养学生学习数学的兴趣和自信心,增强同学之间相互合作、相互交流的意识。
2. 培养学生用数学的眼光看待周围事物。
二、教学重点:灵活运用巧算方法进行计算。
三、教学难点:1. 在进行凑整时,要带上运算符号进行计算。
2. 括号前面是减号,去括号后,括号里原来的符号要进行变号。
四、教学准备:PPT五、教学过程:第一课时(50分钟)一、导入(5分)【设计意图:通过故事,引起学生学习的兴趣,进而引出今天要学习的内容。
】师:上课前,老师想跟你们分享一个小故事,你们想听吗?生:想。
师:在分享故事之前,大家先来看一张图片,这个人大家认识吗?生:不认识。
师:老师来告诉你们,他就是数学家高斯,而今天老师要分享的故事就和他有关系,同学们要仔细听了。
高斯上小学的时候,有一天,他的数学老师在算数课上出了一道难题:“把 1到 100的整数写下来,然后把它们加起来!”每当有考试时他们有如下的习惯:第一个做完的就把石板面朝下地放在老师的桌子上,第二个做完的就把石板摆在第一张石板上,就这样一个一个落起来。
这个难题当然难不倒学过算数级数的人,但这些孩子才刚开始学算数呢!老师心想他可以休息一下了。
但他错了,因为还不到几秒钟,高斯已经把石板放在讲桌上了,同时说道:“答案在这儿!”其他的学生把数字一个个加起来,额头都出了汗水,但高斯却静静坐着,对老师投来的轻蔑的、怀疑的眼光毫不在意。
考完后,老师一张张地检查着石板。
大部分都做错了,学生就吃了一顿鞭打。
最后,高斯的石板被翻了过来,只见上面只有一个数字:5050。
学而思超常班--二年级第二讲图形的拼切

第二讲第4级下·超常班有趣的图形计数 有趣的图形计数1. 数一数.( 15 )个三角形 ( 17 )个正方形 ( 44 )个三角形2. 下图中每个图形各由几个小正方体拼成,至少再增加几个小正方体就可以把这个图形拼成一个长方体?【答案】⑴有9个小正方体,至少增加7个小正方体就可以拼成一个长方体.⑵有10个小正方体,至少增加2个小正方体就可以拼成一个长方体.⑶有12个小正方体,至少增加6个小正方体就⑴ ⑵ ⑶ 有( )个 有( )个 有( )个第二讲第4级下·超常班有趣的图形计数可以拼成一个长方体.3.这堆木方块共有多少块?(中间打阴影部分是空心)【答案】3352339⨯⨯-⨯=(块)或3336239⨯⨯+⨯=(块)或31339⨯=(块).4.下面两个图形能拼成一个长方体吗?【答案】把第二个图形向前打倒,前面的三个可以补在第一个图形的下层,后面的五个可以补在第一个图形的上层,所以说这两个图形能拼成一个长方体.5.如图所示为一堆砖.中央最高一摞是10块,它的左右两边各是9块,再往两边是8块、7块、6第二讲第4级下·超常班有趣的图形计数块、5块、4块、3块、2块、1块.问:这堆砖共有多少块?【答案】当中央最高一摞是10块时,这堆砖的总数是:12345678910987654321++++++++++++++++++ 1010=⨯ 100= (块)6. 将8个小立方块组成“丁”字型,再将表面都涂成红色,然后再把小立方块分开.⑴ 3面被涂成红色的小立方块有( )个. ⑵ 4面被涂成红色的小立方块有( )个. ⑶ 5面被涂成红色的小立方块有( )个.【答案】看着图,想象涂色情况.当把整个表面都涂成红色后,只有那些“粘在一起”的面(又叫互相接触的面),没有被涂色.每个小立方体都有6个面,减去没涂色的面数,就得涂色的面数.每个小立方体涂色面数都写在了它的上面.3面涂色的小立方体共有1个;4面涂色的小立方体共有4个;5面涂色的小立方体共有3个.第二讲第4级下·超常班有趣的图形计数【答案】红球白球一样多。
学而思超常班二年级速算与巧算
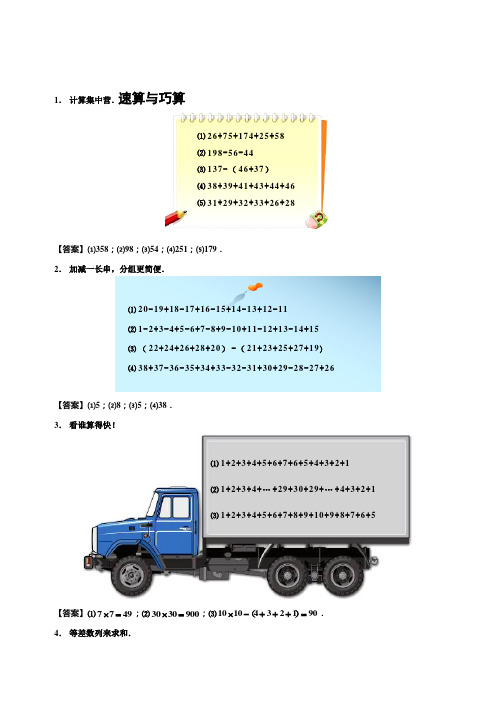
速算与巧算1. 计算集中营.【答案】⑴358;⑵98;⑶54;⑷251;⑸179.2. 加减一长串,分组更简便.【答案】⑴5;⑵8;⑶5;⑷38.3. 看谁算得快!【答案】⑴7749⨯=;⑵3030900⨯=;⑶1010432190⨯-+++=(). 4. 等差数列来求和.⑴1+2+3+4+5+6+7+6+5+4+3+2+1⑵1+2+3+4+…+29+30+29+…+4+3+2+1⑶1+2+3+4+5+6+7+8+9+10+9+8+7+6+5⑴20-19+18-17+16-15+14-13+12-11⑵1-2+3-4+5-6+7-8+9-10+11-12+13-14+15⑶(22+24+26+28+20)-(21+23+25+27+19)⑷38+37-36-35+34+33-32-31+30+29-28-27+26⑴26+75+174+25+58⑵198-56-44⑶137-(46+37)⑷38+39+41+43+44+46⑸31+29+32+33+26+28【答案】⑴7749⨯=;⑵422102130+⨯÷=();⑶54082180+⨯÷=().5. 在下面的□中填上5个连续的数,使等式成立.【答案】67891040++++=.6. 下面的题你会算吗?【答案】135959799++++++L 20003692730------L1995021005022500=+⨯÷=⨯÷=()或50502500=⨯=20003692730200033010220001651835=-+++++=-+⨯÷=-=L ()() ⑴1+3+5+L +95+97+99⑵2000-3-6-9-L -27-30⑴1+3+5+7+9+11+13⑵4+6+8+10+12+14+16+18+20+22⑶5+10+15+20+25+30+35+40【答案】想要把一个西瓜切成9块,我们可以在西瓜上横着切2刀,再竖着切2刀,切成一个“井”字形,这样周围有8块,中间1块,正好9块.这样切成9块的西瓜,吃完后有没有10块西瓜皮呢?只要再想一想,就可以发现,正中间的那一块上下都有瓜皮,把瓜吃完后,这一块有2块瓜皮,不是正有10块瓜皮吗. 豆豆家里来了四位客人,爸爸买了一个大西瓜回来招待客人.但爸爸要求豆豆只许切4刀,切完必须给爷爷、奶奶、爸爸、妈妈、豆豆和四位客人每人一块,而且吃完西瓜后必须有10块瓜皮.请你帮豆豆想一想,该怎样切才合适?。
二年级学而思秋季数学超常班讲义

蜗牛爬井第六讲【例题分析】第6天;可以先考虑特殊的最后一天,蚂蚁爬5米刚好爬到井口,不再滑下,那么它在前几天一共向上移动了205-=15米;它每天爬上5米,又滑下2米,相当于每天只移动了52-=3米,之前爬了153÷=5天,所以第51+=6天爬到井口.一只蚂蚁从一口20米深的枯井底部往上爬,它每天往上爬5米后,就会滑下2米,像这样爬,这只蚂蚁第几天刚好爬到井口?【例题分析】第7天;水缸打水和蜗牛爬井一样,可以先考虑最后一天,这天早上工作人员刚好第一次将水缸装满,那么在此之前水缸里一共有水295-=24桶.每天打回5桶水,又用掉1桶水,则相当于每天往缸里增加51-=4桶水,需要244÷=6天,则第61+=7天第一次把水缸装满.有一口空水缸,需要29桶水才能刚好装满.工作人员每天早上会打回5桶水倒入缸中,傍晚又会用掉缸里1桶水,那么工作人员第几天才能第一次让水缸装满水?【例题分析】第6天;先考虑最后一天,水缸刚好第一次装满,那么在此之前水缸里一共有水216-=15桶.每天倒入6桶水,又用掉3桶水,则相当于每天往缸里增加63-=3桶水,需要153÷=5天,则第51+=6天才能第一次将水缸装满.【例题分析】32米;树懒每天向上爬6米,晚上滑下2米,每天树懒只向上移动了62-=4米.树懒第8天才到顶端,那么前7天共移动了47⨯=28米,再加上第8天的4米,树一共高284+=32米.树懒爬树,它从树底端开始,每天白天向上爬6米,晚上睡觉时滑下2米,第8天爬了4米后终于爬到了树顶端.请问这棵树高多少米?一个空水缸装满水需要21桶,婷婷每天早上向缸里倒入6桶水,晚上又用掉缸里3桶水,婷婷第几天才能第一次将水缸装满?【例题分析】31个;洋洋每次装5个桃子,又吃掉1个,相当于每次只装了514-=个桃子,7次后一共装了7428⨯=个桃子,最后又装3个桃子筐就满了.那么这个筐装满能装28331+=个桃子.【例题分析】18米;小猴爬的最高的位置,是第8次往上爬,还没有滑下来时的位置.小猴每次向上爬4米,然后滑下2米,相当于每次只向上移动了422-=米,第7次时爬到了2714⨯=米的位置,第8次时再往上爬4米到了最高位置,即14418+=米.【例题分析】6米;小丑第8天爬了4米爬到了树顶, 说明前817-=天小丑共向上移动了25421-=米,每天移动了2173÷=米.每次滑下3米,那么每次向上爬336+=米.一个小丑从一棵25米高的树底往上爬,每次向上爬若干米,接着又滑下3米,第8次爬了4米爬到树顶,那么小丑每次向上爬了几米呢?小猴爬竹杆,每次先向上爬4米,接着滑下2米.小猴从竹杆底端开始,共爬了8次,那么小猴最高时爬到了多少米高的位置?洋洋往一个空筐里装桃子,她每次往筐里装5个桃子,然后偷吃掉1个,像这样,第8次装了3个就把筐装满了,那么这个筐装满能装多少个桃子?【例题分析】4米;小蜗牛第6天爬了5米到井口,也就说明前5天一共向上移动了1055-=米,每天移动了551÷=米. 每天白天向上爬5米,则每天夜里会滑下514-=米.【例题分析】42桶;梦梦每天白天打回6桶水,晚上又用掉2桶,相当于每天水缸会增加624-=桶水,30624-=桶,2446÷=天,即第7天打6桶水时,水缸刚好第一次装满.此时梦梦一共打了6742⨯=桶水.一个空水缸,装满需要30桶水,梦梦每天白天会打回6桶水倒入水缸,晚上又会用掉水缸里的2桶水,那么到水缸刚好第一次装满时,梦梦一共打了多少桶水呢?一个空水缸,装满需要33桶水,洋洋每天白天会打回7桶水倒入水缸,晚上又会用掉水缸里的几桶水,第七天洋洋打回3桶水后水缸刚好第一次装满,那么洋洋每天晚上用掉了几桶水呢?小蜗牛从10米深的井底往上爬,每天白天向上爬5米,每天夜里又滑下若干米,第6天爬了5米爬到井口,那么小蜗牛每天夜里滑下了几米呢?【例题分析】64步;舞者先前进4步再后退2步,这样跳一次实际只向前移动了422-=步,24420-= 步,20210÷=次,即第11次时前进4步刚好跳到了另一头.前10次每一次跳了426+=步,这个人一共跳了610464⨯+=步.一位舞者沿一条直线前进4步,接着后退2步,像这样从舞台的一头跳到另一头.舞台的两头相距24步,这个人一共跳了多少步?。
二年级奥数速算、巧算方法及习题

二年级奥数速算、巧算方法及习题速算与巧算在日常生活中,我们经常需要进行简单的数学计算,如加减乘除等。
但是,有些计算可能会让我们感到困惑和繁琐。
为了解决这个问题,我们可以使用速算和巧算的方法。
1.凑整法例如,对于43+88+57这个计算,我们可以将88和57凑成100,然后再加上43,就可以得到188.2.带符号搬家法对于43+88-33这个计算,我们可以将88和33相加,然后再加上43,就可以得到98.这个方法也适用于更复杂的计算。
3.变加为乘法对于8+8+8+8+8+8+8+7这个计算,我们可以将,然后再加上7,就可以得到71.4.加减抵消法对于92-16+23-23+16这个计算,我们可以将16和-16抵消掉,然后再加上23和-23,就可以得到76.5.减法巧算法对于100-36-24和88-(28+15)这两个计算,我们可以直接计算出结果,分别为40和45.6.找基准数法对于52+50+49+46这个计算,我们可以将50和50相加,然后再加上49和51,就可以得到200.7.分组法对于90-89+88-87+86-85+84-83这个计算,我们可以将相邻的数分成一组,然后将每组相加,最后将所有组的结果相加,就可以得到8.8.等差数列法对于1+2+3+……+998+999+1000这个计算,我们可以使用高斯公式,即n×(n+1)÷2,其中n为1000,就可以得到.9.金字塔数列法对于1+2+3+……+98+99+100+99+98+……+3+2+1这个计算,我们可以将它分成两个部分,即1+2+3+……+98+99+100和99+98+……+3+2+1,然后将两部分相加,就可以得到.在使用速算和巧算的方法时,我们需要注意以下几点:1.观察数字和符号的特点,是否能用公式或其他简便方法进行计算。
2.整数比散数好算,小数比大数好算。
3.掌握加法的交换律和结合律,以及带符号搬家、加减括号、减括号等基本理论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
加减法的速算与巧算
一、凑整法:
两个数相加,若能恰好凑成整十、整百、整千、整万…,就说两个数互为“补数”。
10 =
1.计算:
(1)32+17+48 (2)53+36+47 (3)24+44+56 (4)389+163+237 (5)223+168+332 (6)478+243+222
2.计算(拆分凑整):
(1)96+15 (2)52+69 (3)63+18+19 (4)28+28+28 (5)574+498(6)1003+103+13+3
二、减法中的巧算
1.把几个互为“补数”的减数先加起来,再从被减数中减去。
(1)500-75-25 (2)1000-370-330
2.先减去那些与被减数有相同尾数的减数。
(1)566-338-166 (2)843-122-543
三、混合运算改变运算顺序:在只有“+”、“—”号的混合算式中,运算顺序可改变
※带着符号搬家
1.计算:
(1)674+367-174(2)45-18+19
(3)874-(379+274)+579 (4)356+(644-178)
利用“补数”把接近整十、整百、整千…的数先变整,再运算(注意把多加的数再减去,把多减的数再加上)。
(1)506-397 (2)323-189
(3)467+997 (4)987-178-222-390
四、计算等差数列的和
相邻的两个数的差都相等的一串数就叫等差连续数,又叫等差数列,
如(1)1,2,3,4,5,6,7,8,9
(2)1,3,5,7,9
(3)2,4,6,8,10
(4)3,6,9,12,15
(5)4,8,12,16,20 等等都是等差连续数.
1. 等差连续数的个数是奇数时,它们的和等于中间数乘以个数,简记成:
和= 中间数×个数
(1)计算:1+2+3+4+5+6+7+8+9
=5×9 中间数是5 共9个数
=45
(2)计算:1+3+5+7+9 (3)计算:2+4+6+8+10
(4)计算:3+6+9+12+15 (5)计算:4+8+12+16+20+24+28+32+36
2. 等差连续数的个数是偶数时,它们的和等于首数与末数之和乘以个数的一半,简记成:
和=(首数+ 末数)×个数的一半
(1)计算:1+2+3+4+5+6+7+8
=(1+8)×4
=9×4 首+ 末是9 个数的一半是4
=36
(2)计算:3+5+7+9+11+13+15+17
(3)计算:6+8+10+12+14+16+18+20+22+24
3.计算:(1)1+2+3+4+5+6+7+6+5+4+3+2+1
(2)1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2 +1
(3)1+2+3+4+5+6+7+8+7+6+5+4+3
五、基准数法:各加数大小都接近某整十整百的数。
(1)计算:23+20+19+22+18+21
解:仔细观察,各个加数的大小都接近_______,所以可以把每个加数先按_____相加,然后再把少算的加上,把多算的减去.
23+20+19+22+18+21
=
=
=
(2)计算:102+100+99+101+98
(3)计算:83+82+78+79+80+81+78+79+77+84。
