char2冲激函数和其性质
char2冲激函数及其性质

例2: 求y(t)= f (t) * h(t),其中 :h (t) = u(t+1)-u(t-1),
f (t ) T (t )
(t nT ) 解: y(t ) [u (t 1) u (t 1)]* (t nT )
v (t )
v c (0 ) v c (0 ) 0
否则,冲激响应会少一项
第二章 连续系统时域分析
2-2 系统的冲激响应
2)阶跃响应法
1 0.5
sv (t )
(0.5) 0.25
h( t )
第二章 连续系统时域分析
2-3 信号的时域分解和卷积积分
T 2
1)f(t)=fD(t)+fA(t)
2.利用图解法计算
1)f(t)、h(t) f()、h() 2) h() h(-) 4) f() h(t-) 5)计算积分 (折叠) 3) h(-) h(t-) (平移)
(相乘)
f () h( t )d
卷积积分图解法:
f 1 (t ) 1 1 0
阶跃信号 冲激信号 正弦信号 指数信号等
2、系统分析:已知系统模型,研究系统对各种激励信号作用 下的响应特性。
3、信号与系统分析的意义:
(1)信号时间特性与系统时间特性匹配;
(2)信号频率特性与系统频率特性匹配; (3)信号功率特性与系统负载功率匹配; (4)信号信息含量与系统容量匹配; 4、分析方法: 时域法/变域法 内部法/外部法
x(t )
x (t )
x ( k )
0
k (k 1)
二冲激响应——精选推荐
H ( p)
bm pm b1 p b0
N( p)
pn an1 pn1 a1 p a0 D( p)
① n m H ( p) 为真分式
a) 1, 2, , n 特征根均为单根
H ( p) K1 K2 Ki
p 1 p 2
p n
n
h(t) Kieit (t) i1
3
其中
Ki H ( p) ( p i ) pi
b) 1 处 l 重根,其余为单根
H ( p)
K1 p 1
K2 ( p 1)2
Ki ( p 1)i
Kl Kl1 ( p 1)l p l1
Kn p n
重根处系数 Ki 的确定:
Ki
(l
1 R
(t)
1 R2C
t
e RC (t)
uc
(t)
1 C
t i( )d 1
C
t
1 R
(
)d
1 R 2C 2
t
e RC ( )d
1
(t)
1
t
(1 e RC ) (t)
1
t
e RC (t)
RC
RC
RC
例 3 设系统的微分方程为
d 2r(t) 5 dr(t) 6r(t) e(t)
dt 2
eth(t) h(0 )
t
K ( )d Kt (t) KR(t)
0
h(t)
Ktet
(t)
H
(
p)
(
p
K )2
H
(
p)
(
p
K )l
h(t) K tl1et (t) (l 1)!
冲激信号δ(t)的三种定义与相关性质的简单讨论

冲激信号δ(t)的三种定义与相关性质的简单讨论信息科学与工程学院1132班 樊列龙 学号:0909113224有一些物理现象,如理学中的爆炸、冲击、碰撞······,电学中的放电、闪电雷击等,它们都有共同特点: ① 持续时间短. ② 取值极大.冲击函数(或冲击信号)就是对这些物理现象的科学抽象与描述。
通常用δ(t)表示冲激信号,它是一个具有有限面积的窄而高的尖峰信号,它也可以被称作δ函数或狄拉克(Dirac )函数,在信号领域中占有非常重要的地位. 由于冲激函数的特殊性,现给出其两种不严格的定义如下:定义一:用脉冲函数极限定义冲激信号. 如图1-1(a)的矩形脉冲,宽为τ,高为τ1,其面积为A.当A=1称之为单位冲激信号. 现保持脉冲面积不变,逐渐减小τ,则脉冲的幅度逐渐增大,当0→τ时,矩形脉冲的极限成为单位冲激函数,即:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=→221lim )(0τετετδτt t t (1-1)冲击信号的波形就如1-1(b)所示.δ(t)只表示在t=0点有“冲激”,在t=0点以外的各处函数值均为0,其冲激强度(冲激面积)为1,若为A 则表示一个冲击强度为E 倍单位值得函数δ,描述为A=E δ(t),图形表示时,在图1-2箭头旁边注上E 。
也可以用抽样函数的极限来定义δ(t)。
有⎥⎦⎤⎢⎣⎡=∞→)(lim )(kt Sa kt k πδ (1-2)对式(1-2)作如下说明:Θ Sa(t)是抽样信号,表达式为ttt a sin )(S = (1-3) 其波形如图1-2所示,Sa(t)∝1/t, 1/t 随t 的增大而减小,sint 是周 期振荡的,因而Sa(t)呈衰减振荡;并且是一个偶函数,当t=±π,±2π, ···,sint=0,从而Sa(t)=0,是其零点. 把原点两侧两个第一个零点之间的曲线部分称为“主瓣”, 其余的衰减部分称为“旁瓣”。
冲激函数卷积任意函数

冲激函数卷积任意函数一、引言在信号处理领域,卷积是一种重要的运算。
卷积可以用于信号的滤波、特征提取等方面。
其中,冲激函数卷积任意函数是一种常见的卷积方式。
本文将介绍如何编写一个函数来实现冲激函数卷积任意函数。
二、什么是冲激函数在信号处理中,冲激函数是一种特殊的信号。
它在时间为0时取值为无穷大,其它时间点取值都为0。
冲激函数可以用数学公式表示为:delta(t) = {+∞, t=00, t!=0}三、什么是卷积在数学中,两个函数f和g的卷积定义为:(f * g)(t) = ∫f(τ)g(t-τ)dτ其中,*表示卷积运算符,t表示时间变量,τ表示一个虚拟变量。
四、如何计算冲激函数卷积任意函数计算冲激函数与任意函数f(t)的卷积可以分成以下步骤:1. 将f(t)反转得到f(-t)2. 将f(-t)与delta(t)进行卷积得到g(t)3. 将g(t)再次反转得到g(-t)其中,g(t)就是冲激函数与f(t)的卷积结果。
五、函数实现下面是一个Python函数,用于计算冲激函数与任意函数f(t)的卷积:```pythonimport numpy as npdef impulse_convolve(f, t):"""计算冲激函数与任意函数f(t)的卷积Args:f: 任意函数,可以是一个数组或者一个函数t: 时间变量,可以是一个数组或者一个数值范围Returns:g: 冲激函数与f(t)的卷积结果"""# 将f(t)转换为一个可调用的函数if isinstance(f, (list, tuple, np.ndarray)):f = lambda x: np.interp(x, t, f)# 反转f(-t)f_reversed = lambda x: f(-x)# 计算g(t)=delta(t)*f_reversed(-t)g = np.convolve(np.array([1]), f_reversed(t), mode='same')# 反转g(-t)g_reversed = lambda x: g[-x]return g_reversed(t)```六、使用示例下面是一个使用示例:```pythonimport matplotlib.pyplot as plt# 定义任意函数f(t)def f(x):return np.sin(x)**2 + np.cos(2*x)# 定义时间变量范围t = np.linspace(0, 10*np.pi, 1000)# 计算冲激函数与f(t)的卷积g = impulse_convolve(f, t)# 绘制f(t)和g(t)的图像plt.plot(t, f(t), label='f(t)')plt.plot(t, g, label='g(t)')plt.legend()plt.show()```运行以上代码,将会得到一个图像,其中包含了任意函数f(t)和冲激函数与f(t)的卷积结果g(t)的图像。
sql char(2)的用法

sql char(2)的用法
在SQL中,CHAR(n)是一种用来存储固定长度字符串的数据类型,其中n代表字符的最大长度。
对于CHAR(2),它表示存储长度为2
的固定长度字符串。
CHAR数据类型在存储时会使用固定的存储空间,无论实际存储
的字符串长度是多少,空余的位置都会被填充。
例如,如果存储的
字符串长度小于指定的长度,那么剩余的空间会被填充为空格。
在使用CHAR(2)时,需要注意以下几点:
1. 存储空间,CHAR(2)会占用2个字节的存储空间,无论实际
存储的字符串长度是多少。
2. 字符串长度限制,存储在CHAR(2)类型中的字符串长度不能
超过2个字符,否则会被截断。
3. 比较和排序,由于CHAR类型是固定长度的,所以在比较和
排序时会占用固定的存储空间,这可能会影响查询性能。
总之,CHAR(2)用于存储固定长度为2的字符串,适合于长度固定且不太长的数据存储需求。
在实际使用中,需要根据具体的业务需求和数据特点来选择合适的数据类型。
冲激函数和冲激响应
h(t )
1
e
1
ε (t )
t
(8 - 32)
计算冲激响应的另一种方
法是先求出面积为1个单位
的矩形脉冲的响应,然后 求脉冲宽度趋于零的极限。
1 e h ( )
f ( ) g ( )
(8 33)
当△→0时,P(t)趋向于单
位冲激,如图(g)所示,即
lim P (t ) δ (t ) (8 34 )
1 s(t ) (1 e R
R - t L
) (t )
电感电流阶跃响应对时间求导得到iL(t)的冲激响应
t t t ds(t ) 1 1 1 h(t ) (1 e L ) (t ) e L (t ) e L (t ) dt R L L R R R
R t L R
2002年春节摄于成都人民公园
响应的一个方法是先求出电路的阶跃响应s(t),再将它对时
间求导即可得到冲激响应,即利用下式由电路的阶跃响应 计算出电路的冲激响应
ds ( t ) h (t ) dt
(8 31)
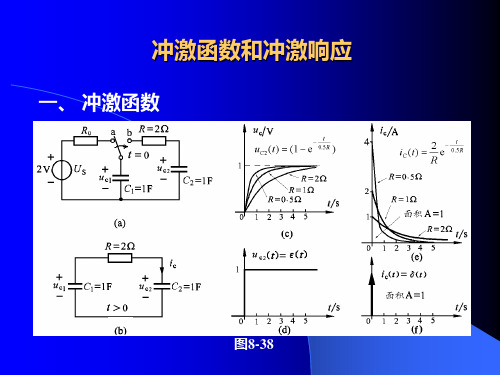
例如图8-35(a)所示RC串联电路的单位阶跃响应为
s(t ) (1 e
其冲激响应为
t RC
) ε (t )
t
当图(b)电路中电阻R趋于零时,电容电压uC2(t)波形趋 于一个单位阶跃,如图(d)所示。而电容电流iC(t)的波形将 变为初始值iC(0+)趋于无限大,时间常数无限小(波形的宽 度趋于零),而面积(电荷量)为一个单位的脉冲,这个极限
的波形称为单位冲激电流,用(t)表示。
当且仅当其满足以下两个性质时,一个无界的信号(t) 称为单位冲激函数
char(2) 的取值范围

`char(2)` 通常指的是在数据库中一个字符型字段的长度限制为2个字符。
具体取值范围取决于多个因素,包括使用的数据库系统、字符集等。
例如,在SQL中,`char(2)`表示该字段可以存储最多2个字符的字符串。
但是,取值范围不仅取决于字段的长度,还取决于数据库系统如何处理超出长度的数据。
例如,如果尝试插入超过2个字符的数据,大多数数据库系统会截断超出部分的数据。
此外,字符集也会影响取值范围。
例如,使用ASCII字符集时,`char(2)`可以存储的字符范围是可打印的ASCII字符,而使用UTF-8等字符集时,`char(2)`可以存储的字符范围更广泛,包括一些特殊符号、非打印字符等。
总的来说,`char(2)`的取值范围取决于数据库系统、字符集以及具体的插入数据。
在处理数据时,应该注意不要超出字段的长度限制,以避免数据截断或其他问题。
冲激偶函数的性质.

冲激偶函数的性质.
冲激函数的性质有:1、筛选性质。
2、取样性质。
3、导数性质。
4、尺度变换性质。
冲激函数是个奇异函数,它是对强度极大、作用时间极短暂且积分有限的一类理想化数学
模型。
冲激函数可用于对连续信号进行线性表达,也可用于求解线性非时变系统的零状态
响应。
冲激函数求导可得到冲激偶函数,单位冲激偶是这样的一种函数:当 t从负值趋于0时,它是一个强度为无限大的正的冲激函数,当t从正值趋于0时,它是一个强度为无限
大的负的冲激函数。
应用领域:
冲激函数可用于信号处理,通过冲激函数来表示复杂的信号,可以简化对复杂信号的
一些特性的研究。
冲激函数及其延时冲激函数的线性组合去则表示或迫近,再利用系统的vary原理,
可以通过直观的信号例如单位冲激函数的频谱,以及频域特性去探讨比较复杂信号的频谱。
从而增加排序繁杂信号频谱的难度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y(t)
1 . 1.(t
1 2
)d
t
y(t) 1 1. 1.(t )d t3 2
t2 t 2 42
y(t) f 1(t) f2 (t) 0
例1:若 h1(t) = u(t), h2(t) = (t-T), h3(t) = - (t), 求h(t) 。
解: h(t) h1(t) h1(t) h2 (t) h3 (t)
第二章 连续系统时域分析
2-1 冲激函数及其性质
一、 冲激函数
定义 u (t) 如图所示:
u (t)
显然当 时0
1
t
u (t) u(t)
0
(t)
du (t) dt
1 (t)
0
t
可认为
lim 0
(t
)
(t
)
即 (t)可视为一个面积始终为1的矩形,当其宽度
趋于零时的极限。
(t) 表示为
(t)
(0.5) 0.25
第二章 连续系统时域分析
2-3 信号的时域分解和卷积积分
T
1)f(t)=fD(t)+fA(t)
其中: f( D t)
[1 T
2 T
f
(t )dt ]
T
f(A t) f (t) fD (t) ——交流分量
—2 —直流分量(平均值)
2)f(t)=fo(t)+fe(t)
如果有 x(t) x(t) x(t) x(t)
上式从t 0到 t 0 取积分,得
R
0
0 iL (t)dt
LiL (0
)
LiL (0 )
1
由于i
L
(t
)是有限的,0 0
i
L
(t
)dt
0且iL (0 )
0iL (0 )
1 L
第二章 连续系统时域分析
2-2 系统的冲激响应
电感电流在冲激信号作用下,从零跃变到 1 L
当 t 0 时, (t) 0, 此时电路是一个特殊的
5)计算积分
f () h(t )d
卷积积分图解法:
f1(t )
1 f1(t ) 0
f1( )
t 1 ,
t 1
t f2(t) 2 ,
(0 t 3)
1
t
1 0 1 t
1
f2 (t )
f2 (t f2)(t ) f2 (t )f2 (t )
1 0
1
t
3
t 3 tt 3
x(k)
t
0
k (k 1) 这些矩形叠加起来形成
阶梯信号
3)任意连续时间信号可分解为冲激信号的连续和
x(t)
x (t)
x(k)
t
0
k (k 1)
当 时0 , k d
(t k) (t )
x (t) x(t)
于是: x(t)
x( ) (t )d
3)任意连续时间信号可分解为冲激信号的连续和
零输入响应。 由三要素公式得
iL (t)
1 L
R t
e L (t)
h(t)
第二章 连续系统时域分析
2-2 系统的冲激响应
2)阶跃响应法 u(t) g(t) (t) h(t)
激励为 lim (t) (t t) d (t) (t)
t 0
t
dt
响应为 lim s(t) s(t t) ds(t) h(t)
尺度变换 (at) 1 (t)
|a|
du(t) (t) dt
(t) 的倒数及其性质
f
(t)
' (t
t0 )dt
f
' (t0 )
f (t) ' (t t0 ) f (t0 ) ' (t t0 ) f ' (t0 ) (t t0 )
(k) (t) (1)(k) (k) (t)
f (t) (t T) f (t T)
f (t)*u(t t0 )
tt0 f ( )d
f (t )d t0
f (t t0) (t T ) f (t t0 T ) 例: u(t)*u(t) tu(t)
2、f(t)与冲激信号偶卷积 4、斜坡信号与阶跃信号卷积
f (t) (t) f (t)
x(t) h1(n) h2 (n) y(t) x(t) [h1(t) h2 (t)]
h1(t) h2 (t)
h1(t) x(n) h1(n)
x(n)
h1(n)
y(n)
x(t)
y(t)
h2 (n)
h2 (t)
x(n) h2(n)
第二章 连续系统时域分析
结论:两个LTI系统并联,其总的单位脉冲(冲激)响 应等于各子系统单位脉冲(冲激)响应之和。
如果解决了信号分解的问题,即:若有
x(t) ai xi (t)
i
则 y(t) ai yi (t)
i
分析方法:
xi (t) yi (t)
将信号分解可以在时域进行,也可以在频域或变换 域进行,相应地就产生了对LTI系统的时域分析法、 频域分析法和变换域分析法。
信号与系统分析 1、信号分析:复杂信号 分解
1.交换律
y(t) x(t) h(t) x( )h(t )d x(t )h( )d h(t) x(t)
h(n)
x(n)
x(t) x(n)
h(t)
y(t) y(n)
h(t) h(n)
x(t)
y(t) y(n)
结论:一个单位冲激响应是 h的(t)LTI系统对输入信
号 所x(t产) 生的响应,与一个单位冲激响应是
这种求得系统响应的运算关系称为卷积积分
II 、卷积积分的计算
1.利用定义计算
f (t) h(t)
f ( ) h(t )d
h() f (t )d
2.利用图解法计算
1)f(t)、h(t) f()、h() 2) h() h(-) (折叠) 3) h(-) h(t-) (平移) 4) f() h(t-) (相乘)
第二章 连续系统时域分析
2-0 引言
由于LTI系统满足齐次性和可加性,并且具有时 不变性的特点,因而为建立信号与系统分析的理 论与方法奠定了基础。
基本思想:如果能把任意输入信号分解成基本信号 的线性组合,那么只要得到了LTI系统对基本信 号的响应,就可以利用系统的线性特性,将系统 对任意输入信号产生的响应表示成系统对基本信 号的响应的线性组合。
[x(t)
x(t)]
xe
(t)
1 2
[x(t)
x (t )]
xo
(t)
1 2
[x(t)
x (t )]
3)任意连续时间信号可分解为冲激信号的连续和
对一般信号 x(t,) 可以将其分成很多 宽度的区段,
用一个阶梯信号 近x似 (t表) 示 。当x(t) 时,有 0 x (t) x(t)
x(t) x (t)
1
t
0
(t t0 )
1
t
0 t0
矩形面积称为冲激强度。
显然有:
(t)dt 1
t
u(t)
( )d
0
(t
)d
第二章 连续系统时域分析
2-1 冲激函数及其性质
二、性质
加权特性 f (t) (t t0 ) f (t0 ) (t t0 )
偶函数 (t) (t)
单位阶跃函数的倒数
第二章 连续系统时域分析
2-2 系统的冲激响应
激励为单位冲激信号时系统的零状态响应。
由于冲激函数及其各阶导数仅在t=0处作用, 而在t>0的区间恒为零。也就是说,激励信号 的作用是在t=0的瞬间给系统输入了若干能量, 贮存在系统的各贮能元件中,而在t>0系统的 激励为零,只有冲激引入的那些贮能在起作 用,因而,系统的冲激响应由上述贮能唯一 地确定。
阶跃信号
基本信号
冲激信号 正弦信号
复杂信号特性
基本信号特性 指数信号等
2、系统分析:已知系统模型,研究系统对各种激励信号作用 下的响应特性。
3、信号与系统分析的意义: (1)信号时间特性与系统时间特性匹配;
(2)信号频率特性与系统频率特性匹配; (3)信号功率特性与系统负载功率匹配; (4)信号信息含量与系统容量匹配; 4、分析方法:时域法/变域法 内部法/外部法
u(t
n
1)]*
(t nT )
[u(t 1 nT ) u(t 1 nT )]
n
n
例6:用图解法求y(t)=f(t)*h(t)。其中
解: 当t<0: y(t) f (t)h(t) 0 当0<t<7:y(t) t e(t)d
0
1 et
当7<t: y(t)
7 e(t)d (e7 1)et
t 3t t t3
t
t
f2 (t )
3 2
0
3t
f2 ( )
3 2
3
0
y当当(tt-)<1-<y1(tt<)tf412tt1(2f1)y(t2t()ftt2)(tf124(2tt1))f1(00)
1 t 1 1t 2 f22 (tt)d4
4 0
2
t2 4
t 2
1 4
其它t
当1<t<2 当2<t<4
f( ) (t - )d f (t)
-
f( )h(t - )d y f (t)
-
f()(t-) f()h(t-)
此称为f(t)与h(t)的卷积积分
(Convolution)
f( ) (t - )d
