2012数学建模优秀论文 葡萄酒
2012年全国大学生数学建模竞赛a题 葡萄酒的评价 答案.

葡萄酒的评价摘要本文主要研究的是如何对葡萄酒进行评价的问题。
通过对评酒员的评分与酿酒葡萄的理化指标和葡萄酒的理化指标等原始数据进行统计、分析和处理,我们得出了一个较为合理地评价葡萄酒质量优劣的模型。
在问题一中,我们采用T检验法,首先进行正态分布拟合检验,判断出它们服从正态分布。
之后,我们通过T检验法判断出了两组评酒员的评价结果具有显著性差异。
而对于如何判断哪一组评酒员的评价结果更可信,由于评酒员评分的客观性,我们通过计算评酒员评分均值的置信区间,利用置信区间的长短来判断评分的可信程度。
置信区间越窄,说明其越可信。
利用Matlab软件求出了第二组评酒员的评分均值的置信区间更窄,所以第二组评酒员的评价结果更可信。
在问题二中,我们采用主成分分析法,把给定的一组相关变量通过线性变换转成另一组不相关的变量,这些新的变量再按照方差依次递减的顺序排列。
在数学变换中保持变量的总方差不变,使第一变量具有最大的方差。
第二变量的方差次大,并且和第一变量不相关。
由于变量较多,虽然每个变量都提供了一定的信息,但其重要性有所不同。
依次类推,最后我们将酿酒葡萄分为了四个等级:优质、次优、中等、下等。
在问题三中,我们通过多项式曲线拟合的方法,构造一个以葡萄酒的理化指标为自变量,酿酒葡萄的理化指标为因变量的函数,并利用Matlab软件进行曲线拟合,最后得出酿酒葡萄与葡萄酒的理化指标之间的关系为呈线性正相关。
在问题四中,我们用无交互作用的双因素试验的方差分析方法,通过对观测、比较、分析实验数据的结果,鉴别出了两个因素在水平发生变化时对实验结果产生显著性影响的大小程度。
最后,我们认为能用酿酒葡萄和葡萄酒的理化指标来评价葡萄酒的质量,且酿酒葡萄的理化指标对葡萄酒质量影响相对葡萄酒的理化指标更显著。
关键词:T检验法,Matlab,正态分布,主成分分析法,多项式曲线拟合,方差分析一.问题的重述确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
2012年高教杯数学建模竞赛获奖论文资料

葡萄酒的评价摘要:本文针对葡萄酒的评价问题建立了相应的统计模型。
问题一:借助SPSS软件,建立数值显著性分析模型和数值可信度分析模型。
首先,将每位评酒员对某种葡萄酒的分类指标打的分值求平均值并求和,即该种葡萄酒的质量,依此可得到每种葡萄酒的质量;其次,利用单因素分析法分别得到红葡萄酒组和白葡萄酒组的F值,用F检验法分别判断出两组评判结果针对红、白葡萄酒均存在显著性差异;再次,由方差分析法,分析出第二组的评判结果的可信度更高,故可将此组结果作为葡萄酒的质量。
问题二:在所有数值进行无量纲化处理的前提下,结合SPSS软件利用因子分析法构造出酿酒葡萄的综合理化指标函数,得到每种葡萄的综合理化指标,结合所酿葡萄酒的质量,进一步得到每种酿酒葡萄的综合得分。
根据每种酿酒葡萄的综合得分,利用极差分析法构造函数,划分等级范围,进而对葡萄分级。
问题三:由于酿酒葡萄和葡萄酒的量化指标数目的不同,为了更全面的考虑两者之间的联系,利用其综合理化指标分析两者之间的理化指标间的联系。
葡萄酒的综合理化指标与问题二中酿酒葡萄的综合理化指标处理方法一样。
根据相关性分析法,利用SPSS软件计算得到红葡萄与红葡萄酒的综合理化指标、白葡萄与白葡萄酒的综合理化指标均存在相关性。
针对问题四:基于问题二、三的结果,将酿酒葡萄和葡萄酒的理化指标用综合理化指标描述,将其看做自变量,将葡萄酒的质量看做因变量,结合SPSS软件对其进行线性回归分析,得到回归函数。
由于,一般认为评酒员对葡萄酒的评价结果就是葡萄酒的质量,因此利用该回归函数得到的葡萄酒的质量与评酒员打分所得中的葡萄酒质量比较发现差异较大,根据相关性系数和资料可得,葡萄酒的质量不仅仅与这两个因素有关,对其论证分析,发现酿酒葡萄和葡萄酒中的芳香类物质对专家打分有一定的影响,因此可基于芳香类物质对所得回归函数进行进一步完善,从而得到更优的葡萄酒质量评价模型。
关键词:单因素方差分析无量纲化处理因子分析法综合指标函数回归分析1.问题重述确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
2012年全国大学生数学建模A题--葡萄酒质量的评价分析

葡萄酒质量的评价分析摘要本文主要讨论了葡萄酒和葡萄的理化指标与葡萄酒质量的关系。
通过品酒员对样品酒的外观,香气,口感的评分数据与所酿葡萄酒的理化指标和对酿酒葡萄的化学分析来确定葡萄酒质量好坏以及它们之间的关系。
根据附录中所给的两组品酒员分别对红葡萄酒和白葡萄酒进行品尝后的评分数据和各种理化指标进行了严谨的分析之后,继而运用适当的数学软件结合数学模型进行大量的拟合数据分析。
在葡萄酒品尝评分表中,由于品酒员对葡萄酒的要求、口感及其他各方面的主观条件存在一定的差异,因此,我们对品酒员给出的评分数据进行了客观的分析,降低品酒员主观造成的误差,客观的反映了样品酒之间的真实差异,同时将酿酒葡萄进行了等级划分。
并通过所给的理化指标数据和芳香物质含量更加准确的描述了酿酒葡萄、葡萄酒、葡萄酒质量之间的联系。
对于问题一,题目中要求我们判断两组品酒员的评价结果有无显著性差异,哪一组结果更可信。
由于题中数据量很大,且杂乱无章,很难直接看出,因此我们将数据在统计图中进行表示,观察了数据的稳定情况,为了更好的表达数据的稳定情况,我们采用了求每组数据方差的方法,通过比较,得出两组品酒员的评价结果存在显著性差异,且第二组品酒员所给的评分更为可信。
对于问题二,题目要求根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级,由问题一所得结果可知,第二组评分更为可信,故直接采用第二组数据进行分析。
将该数据进行数学期望处理,得到了十位评委对每种样品酒的平均打分,我们根据帕克评分系统的标准[1]将样品酒进行了分级。
对于问题三,我们使用了EXCEL中拟合数据分析的功能来探究酿酒葡萄与葡萄酒的各项理化指标之间的联系。
经过对得到的散点图不断的尝试各种函数图像,最终我们找到了最适合它们之间关系的也就是散点落在函数图象外最少的数学函数图像,从而得到该图像的数学表达式。
由于图表中显示酿酒葡萄与葡萄酒对应的各项指标存在多项式函数关系,所以我们得出结论,酿酒葡萄与葡萄酒各项理化指标存在着多项式函数的联系。
2012数学建模A题葡萄酒答案
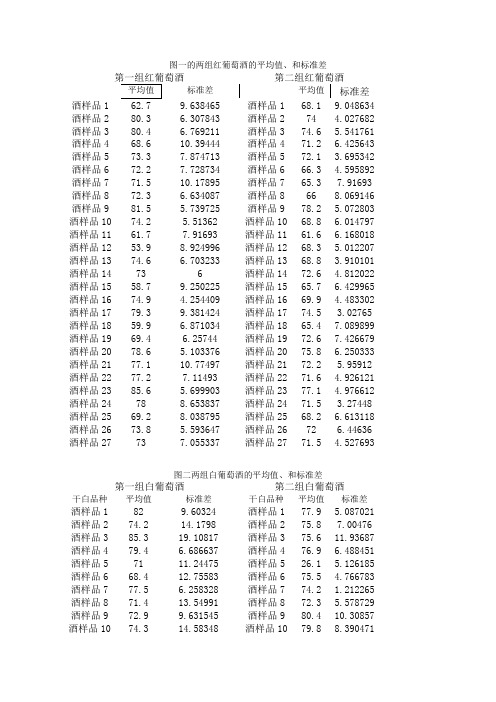
图一的两组红葡萄酒的平均值、和标准差第二组红葡萄酒标准差平均值标准差酒样品1 9.638465 酒样品1 68.1 9.048634 酒样品2 80.3 6.307843 酒样品2 74 4.027682 酒样品3 80.4 6.769211 酒样品3 74.6 5.541761 酒样品4 68.6 10.39444 酒样品4 71.2 6.425643 酒样品5 73.3 7.874713 酒样品5 72.1 3.695342 酒样品6 72.2 7.728734 酒样品6 66.3 4.595892 酒样品7 71.5 10.17895 酒样品7 65.3 7.91693 酒样品8 72.3 6.634087 酒样品8 66 8.069146 酒样品9 81.5 5.739725 酒样品9 78.2 5.072803 酒样品10 74.2 5.51362 酒样品10 68.8 6.014797 酒样品11 61.7 7.91693 酒样品11 61.6 6.168018 酒样品12 53.9 8.924996 酒样品12 68.3 5.012207 酒样品13 74.6 6.703233 酒样品13 68.8 3.910101 酒样品14 73 6 酒样品14 72.6 4.812022 酒样品15 58.7 9.250225 酒样品15 65.7 6.429965 酒样品16 74.9 4.254409 酒样品16 69.9 4.483302 酒样品17 79.3 9.381424 酒样品17 74.5 3.02765 酒样品18 59.9 6.871034 酒样品18 65.4 7.089899 酒样品19 69.4 6.25744 酒样品19 72.6 7.426679 酒样品20 78.6 5.103376 酒样品20 75.8 6.250333 酒样品21 77.1 10.77497 酒样品21 72.2 5.95912 酒样品22 77.2 7.11493 酒样品22 71.6 4.926121 酒样品23 85.6 5.699903 酒样品23 77.1 4.976612 酒样品24 78 8.653837 酒样品24 71.5 3.27448 酒样品25 69.2 8.038795 酒样品25 68.2 6.613118 酒样品26 73.8 5.593647 酒样品26 72 6.44636 酒样品27 73 7.055337 酒样品27 71.5 4.527693图二两组白葡萄酒的平均值、和标准差第一组白葡萄酒第二组白葡萄酒干白品种平均值标准差干白品种平均值标准差酒样品1 82 9.60324 酒样品1 77.9 5.087021 酒样品2 74.2 14.1798 酒样品2 75.8 7.00476 酒样品3 85.3 19.10817 酒样品3 75.6 11.93687 酒样品4 79.4 6.686637 酒样品4 76.9 6.488451 酒样品5 71 11.24475 酒样品5 26.1 5.126185 酒样品6 68.4 12.75583 酒样品6 75.5 4.766783 酒样品7 77.5 6.258328 酒样品7 74.2 1.212265 酒样品8 71.4 13.54991 酒样品8 72.3 5.578729 酒样品9 72.9 9.631545 酒样品9 80.4 10.30857 酒样品10 74.3 14.58348 酒样品10 79.8 8.390471酒样品11 72.3 13.30873 酒样品11 71.4 9.371351 酒样品12 63.3 10.76052 酒样品12 72.4 11.83404 酒样品13 65.9 13.06777 酒样品13 73.9 6.838616 酒样品14 72 10.68748 酒样品14 77.1 3.984693 酒样品15 72.4 11.4717 酒样品15 78.4 7.351493 酒样品16 74 13.34166 酒样品16 53.1 9.06826 酒样品17 78.8 12.00741 酒样品17 80.3 6.201254 酒样品18 73.1 12.51177 酒样品18 76.7 5.498485 酒样品19 72.2 6.811755 酒样品19 76.4 5.103376 酒样品20 77.8 8.024961 酒样品20 43.2 7.07421 酒样品21 76.4 13.14196 酒样品21 79.2 8.024961 酒样品22 71 11.77568 酒样品22 79.4 7.321202 酒样品23 75.9 6.607235 酒样品23 77.4 3.405877 酒样品24 73.3 10.54145 酒样品24 76.1 6.208417 酒样品25 77.1 5.820462 酒样品25 79.5 10.31988 酒样品26 81.3 8.53815 酒样品26 74.3 7.532168 酒样品27 64.8 12.01666 酒样品27 77 5.962848 酒样品28 81.3 8.969702 酒样品28 79.6 5.037636描述统计量N 均值标准差方差统计量统计量标准误统计量统计量VAR00003 27 68.5185 1.50722 7.83174 61.336 VAR00004 27 74.4444 2.24201 11.64980 135.718 VAR00005 27 72.7037 2.70265 14.04338 197.217 VAR00006 27 65.2963 1.44393 7.50290 56.293 VAR00007 27 74.1852 2.64469 13.74223 188.849 VAR00008 27 72.7037 2.13091 11.07254 122.601 VAR00009 27 71.2222 1.51002 7.84628 61.564 VAR00010 27 72.0741 1.95456 10.15619 103.148 VAR00011 27 78.4444 1.23035 6.39311 40.872 VAR00012 0Zscore(VAR00003) 0Zscore(VAR00004) 0Zscore(VAR00005) 0Zscore(VAR00006) 0Zscore(VAR00007) 0Zscore(VAR00008) 0Zscore(VAR00009) 0Zscore(VAR00010) 0Zscore(VAR00011) 0Zscore(VAR00012) 0描述统计量N 均值标准差方差统计量统计量标准误统计量统计量VAR00003 27 68.5185 1.50722 7.83174 61.336 VAR00004 27 74.4444 2.24201 11.64980 135.718 VAR00005 27 72.7037 2.70265 14.04338 197.217 VAR00006 27 65.2963 1.44393 7.50290 56.293 VAR00007 27 74.1852 2.64469 13.74223 188.849 VAR00008 27 72.7037 2.13091 11.07254 122.601 VAR00009 27 71.2222 1.51002 7.84628 61.564 VAR00010 27 72.0741 1.95456 10.15619 103.148 VAR00011 27 78.4444 1.23035 6.39311 40.872 VAR00012 0Zscore(VAR00003) 0Zscore(VAR00004) 0Zscore(VAR00005) 0Zscore(VAR00006) 0Zscore(VAR00007) 0Zscore(VAR00008) 0Zscore(VAR00009) 0Zscore(VAR00010) 0Zscore(VAR00011) 0Zscore(VAR00012) 0有效的 N (列表状态)0模型描述模型名称MOD_2因变量 1 VAR000032 VAR000073 VAR000054 VAR000115 VAR00008方程 1 二次自变量VAR00004常数包含其值在图中标记为观测值的变量未指定用于在方程中输入项的容差.0001个案处理摘要N变量处理摘要变量因变量自变量VAR00003 VAR00007 VAR00005 VAR00011 VAR00008 VAR00004 正值数27 27 27 27 27 27 零的个数0 0 0 0 0 0 负值数0 0 0 0 0 0 缺失值数用户自定义缺失0 0 0 0 0 0 系统缺失0 0 0 0 0 0模型描述模型名称MOD_2因变量 1 VAR000032 VAR000073 VAR000054 VAR000115 VAR00008方程 1 二次自变量VAR00004常数包含其值在图中标记为观测值的变量未指定用于在方程中输入项的容差.0001个案处理摘要N个案总数27已排除的个案a0模型描述模型名称MOD_2因变量 1 VAR000032 VAR000073 VAR000054 VAR000115 VAR00008方程 1 二次自变量VAR00004常数包含其值在图中标记为观测值的变量未指定用于在方程中输入项的容差.0001模型描述模型名称MOD_2因变量 1 VAR000032 VAR000073 VAR000054 VAR000115 VAR00008方程 1 二次自变量VAR00004常数包含其值在图中标记为观测值的变量未指定用于在方程中输入项的容差.0001。
2012全国大学生数学建模竞赛A题 葡萄酒的评价

A题葡萄酒的评价确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:1. 分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。
4.分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?对问题的分析与类比归纳:1、笔者认为,对于同一事物的评价 如果大家的意见越一致 那么评价的可信度就越高。
所以对于问题1的解题思路也就清晰明了了. 我们可以通过方差。
所谓方差即观测变量各个取值之间的差异程度。
它是用以衡量风险大小的指标。
这一概念来对每一组评酒员作出的评估作出风险分析。
显而易见的是若风险评估的值越高 这组评酒员的评价就存在问题了。
若风险评估值大小相当 这说明这两组评酒员是没有明显差异的。
2、题目中要求对葡萄作出评级。
看起来似乎没有思路 那么我们可以动一下我们的小脑筋。
既然对于评级我们没有参考标准 那么我们可以参考评酒员的评价。
即使用逆向思维 从评酒员的评分发出 那么大体上葡萄的分级基本上就能确定下来 根据确定先来的葡萄分级进行逆推 就可以得出结论。
3、对于这个问题 最直观也是最基本的思路就是看两者之间的趋势。
应用MATLAB软件,作出两者的趋势图。
通过对趋势图的直接观察 两者之间的大体关系即可确定 然后根据曲线拟合的方法可得出两者间的函数关系。
可以类比手机套餐问题解决归纳。
对于我们这些消费用户来说,手机的资费问题一直是我们所关注的热点问题。
2012年数学建模A题一等奖获奖论文

秩和得到一个新的排序。由于此排序综合了 20 个评酒员的结果,因此,更能反 应酒样的排序真实性,即认为该综合排序为理想排序。记样品 j 在第一组、第二 组排序内的秩次为 X j (1) , X j (2) ,综合之后排序秩次为 X j 。红葡萄酒三种排序的 比较图如下:
关键词:葡萄酒评价
排序检验法
符号秩检验
TOPSIS 法
多重比较
1
一、问题重述
对于葡萄酒质量的确定,现如今通常采用感官评价的方法,即聘请一批有资 质的品酒员对葡萄酒进行品评,然后对其外观、口感等分类指标进行打分。最后 通过求和得到每种葡萄酒的总分,从而确定葡萄酒的质量。附件 1 中给出了某一 年份一些葡萄酒的打分结果。 同时,酿酒葡萄的好坏又直接影响着所酿葡萄酒的质量。除了感官评价的方 法之外,在某种程度上,葡萄酒和酿酒葡萄检测的理化指标也能反映葡萄酒和葡 萄的质量。附件 2 和附件 3 即给出了同一年份中,这些葡萄酒的和酿酒葡萄的成 分数据。 请分析题目,试建立合适的数学模型解决以下问题: 1. 对于附件 1 中的红葡萄酒与白葡萄酒, 每种葡萄酒均由两组评酒员对其进 行打分。试分析这两组品酒员的评价结果有无显著性差异,并判断哪一组的结果 更为可信。 2. 综合感官评价所得到的葡萄酒质量与酿酒葡萄的理化指标,对酿酒葡萄 进行分级。 3. 试分析酿酒葡萄、葡萄酒的两组理化指标之间有何关系。 4. 分析酿酒葡萄的理化指标、葡萄酒的理化指标对葡萄酒质量的影响,论 证能否只用葡萄和葡萄酒的理化指标来评价葡萄酒的质量。
3
分的差异是否在一定的置信区间内,若不在,则认为评分差异性显著。 考虑到本题的背景,两组评分的差异可体现在对样本酒的排名差异上。由于 该问属于食品评价中的感官评价问题,因此,可结合感官评价中的排序检验与非 参数检验中的符号秩检验,对两组评分的显著性进行评价。 1.1.1 样品秩次和秩和的求解 评酒员对每一个酒样均从四大方面进行了评分。根据题意,葡萄酒的质量由 总分所确定。 因此, 我们将每一个方面的评分加和, 得到 i 品酒员对葡萄酒样品 j 的总评分。 以红葡萄酒的评价为例,对于品酒员 i ,将其对 27 种样品的评分进行排序, 评分最高的酒样秩次为 1,当多个样品有相同秩次时,则取平均秩次。记在 i 品 酒员的评价排序中, j 酒样的秩次为 xij ,可得到秩次矩阵为:
葡萄酒的鉴定 2012年数模国赛A题论文
关键字 :t 检验
主成分析法
典型相关分析
多元线性回归
1
一、问题重述
1.1 问题的背景 确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。 每个评酒 员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定 葡萄酒的质量。酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和 酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。附件 1 给 出了某一年份一些葡萄酒的评价结果,附件 2 和附件 3 分别给出了该年份这些 葡萄酒和酿酒葡萄的成分数据。 1.2 问题的提出 请尝试建立数学模型讨论下列问题: 1. 分析附件 1 中两组评酒员的评价结果有无显著性差异, 哪一组结果更可信? 2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。 3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。 4.分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡 萄和葡萄酒的理化指标来评价葡萄酒的质量?
二、基本假设
1、假设所有的数据都是可靠的,不包括人为造成的不合理因素。 2、假设数据中的奇异数据和缺省值忽略后对总体信息不会有显著的影响。 3、评酒师对葡萄酒的质量打分能真实的反映葡萄酒质量的好坏。 4、忽略酿酒葡萄和葡萄酒的色泽对酒样品质量的影响。 5、酿酒葡萄的各理化指标,如蛋白质、氨基酸含量在正常范围内越高越好。
5
我们对附件一中的各个评酒员给各种酒的指标打的分数相加之后, 按照酒的 序号分红葡萄酒、白葡萄酒进行排序,见附件 2. 我们对先对第一组的十个评酒员对白葡萄酒的打分总分的一组数据数据进行处 理,把前面处理的数据输入到 SPSS 中,得到的 Q—Q 图,它的 sig 值为 0.449, 大于 0.05,所以所给数据服从正态分布。
数学建模论文---葡萄酒的评价
数学建模论文---葡萄酒的评价承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):4198所属学校(请填写完整的全名):广东医学院(东莞校区)参赛队员(打印并签名) :1. 黄洁2. 顾家荣3. 陈婉君指导教师或指导教师组负责人(打印并签名):唐国平日期:2013年9月 9日编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):葡萄酒质量的评价模型摘要本文主要讨论了关于葡萄酒与葡萄之间关系的研究,主要分析了附件1中两组评酒员的评价结果有无显著性差异,并判断哪一组结果更可信;还根据酿酒葡萄的理化指标和葡萄酒的质量把这些酿酒葡萄分为3个等级;分析了酿酒葡萄与葡萄酒的理化指标之间的联系和酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证用葡萄和葡萄酒的理化指标来评价葡萄酒的质量。
通过这些分析有益于对葡萄酒行业的发展有一定的贡献。
对于问题一,用10个品酒员对每种酒样品的总评分的来代表这种酒样品的质量,建立单因子数学模型,分别对两个水平进方差分析,由U检验,取置信区间为95%,最终得出两组品酒员对红葡萄酒的评分有显著性差异,对白葡萄酒的评分没有显著性差异。
2012高教社杯全国大学生数学建模竞赛
A题葡萄酒的评价摘要本文主要研究葡萄酒质量与酿酒葡萄理化指标以及葡萄酒自身的理化指标之间的联系的问题,我们根据题目所给定的一些数据和信息分析并建立了方差分析模型,聚类分析模型,因子分析和主成分分析以及拟合回归等模型解决问题。
问题一首先在原始表格中对数据整理求均值,建立正态模型,分析评价结果是否服从正态分布。
再用SPSS软件分别计算出第一组和第二组品酒师对红葡萄酒和白葡萄酒总评分之间的方差分析表,得到F检验的数值,判断第一组和第二组品酒师的评分是否有显著性差异。
然后再对每组品酒师对各项指标的评分,总评分求标准差,标准差越大说明该组品酒师的分数更具有波动性,其可信度就相对小;反之,其可信度就相对大。
问题二主要运用聚类分析法对酿酒葡萄进行分级。
首先由于各个指标的量纲不统一,所以分类前将其标准化,即做变换Pik =(xik-kμ)/kσ (i=1,2,...,27;k=1,2, (11)F it=(yit -tμ)/tσ (i=1,2,...,28;t=1,2, (10)再求不同品种葡萄酒的相同理化指标之间的欧式标准距离,距离越小,说明两个品种越接近,划为一类的机会就越大。
建立聚类分析模型,用matlab求解。
问题三主要运用相关分析的方法。
先跟据附表2中所给酿酒葡萄和葡萄酒的理化指标数据作出假设。
原假设H0;P=0 备择假设H1;P~=0建立相关系数模型,给定显著性水平值,用SPSS软件得出相关分析表并计算得出相关系数和显著性值P,根据表格中相关系数和显著性值进行分析比较。
在用SPSS计算过程中给定两个显著性水平值a.b,分别计算出在a显著性水平下的相关性和b在显著性水平下的相关性,从而表现出酿酒葡萄中元素和葡萄酒中理化指标的相关性强弱关系,进一步分析出酿酒葡萄和葡萄酒理化指标之间的联系。
问题四主要运用多元线性回归分析对葡萄酒质量及其影响因素之间的关系作出分析。
再利用一和三问中得出的结果,建立多元回归模型并运用SPSS软件求其多元线性回归方程。
2012年高教社杯全国大学生数学建模竞赛A题全国一等奖论文
葡萄酒的评价摘要本文主要对两组评酒员的评价结果及可信度、酿酒葡萄的分级、酿酒葡萄与葡萄酒的理化性质之间的联系和是否影响葡萄酒的质量进行分析及研究。
对于问题一,利用附件一中评酒员群体对红、白葡萄酒进行两次评分的数据,运用t检验模型,求出P值用于判定有无显著性差异。
出于对结果的科学性考虑,建立了二值化可信度模型对评酒员的可信度进行定量描述。
若可信度值i p越大,则说明评价结果越可信。
通过比较第一、二组的P值,得出第一组的可信度更高些。
对于问题二,运用主成分分析法,选取葡萄酒样品中含有的一级指标物的数据,得出贡献率。
再利用贡献率(贡献率越大对葡萄的质量影响越大)的大小,选出影响酿酒葡萄分级的主成分因素,并利用红地球葡萄的分级标准对酿酒葡萄进行分级。
对于问题三,首先利用主成分分析法和SPSS软件对红葡萄酒的量化指标进行筛选,选出总酚、酒总黄酮、白藜芦醇等6种物质作为对葡萄酒理化指标的一组样本。
借用在问题二中筛选出来的花色苷、干物质含量、顺式白藜芦醇苷等六种红葡萄的理化指标作为另一组样本。
然后利用上述两组数据,建立典型相关分析模型,求出葡萄酒理化指标和酿酒葡萄的相关系数,从而确定两者之间的关联度。
最后建立二元回归模型进而求出两者之间的关系。
对于问题四,运用主成分分析降维的思想,运用灰色关联度模型,利用几组变量的数据,通过MATLAB软件求得关联度,进而来反映两变量之间的线性关系。
根据关联度的大小,考虑多方面的因素对葡萄酒的质量进行评价与论证。
关键词:t检验法、可信度模型、主成分分析法、多元回归模型、灰色关联度1 问题重述确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏师范大学
第五届(2011)数学建模竞赛
我们选择的题号是: B
我们的参赛队号为:
2012江苏师范大学数学建模竞赛题目
B题研究生录取问题
摘要:根据问题的背景和题目要求,研究在不同条件的研究生录取问题,在对笔试,面试以及导师信息量化,加权平均求解的基础来解决研究生录取的问题。
通过构造选择矩阵和满意度矩阵建立导师和学生之间的双向选择矩阵的0-1规划模型。
利用测发编程计算求出最优解,从而求得问题的最优方案,同时采用降阶技巧和创建定理,快速的求解出实用的最优解,得到对应的最优方案!
一问题重述
某学校M系计划招收10名计划内研究生,依照有关规定由初试上线的前15名学生参加复试,专家组由8位专家组成。
在复试过程中,要求每位专家对每个参加复试学生的以上5个方面都给出一个等级评分,从高到低共分为A,B,C,D四个等级,并将其填入面试表内。
所有参加复试学生的初试成绩、各位专家对学生的5个方面专长的评分。
该系现有10名导师拟招收研究生,分为四个研究方向。
导师的研究方向、专业学术水平(发表论文数、论文检索数、编(译)著作数、科研项目数),以及对学生的期望要求。
在这里导师和学生的基本情况都是公开的。
要解决的问题是:
(1) 首先,请你综合考虑学生的初试成绩、复试成绩等因素,帮助主管部门确定10名研究生的录取名单。
然后,要求被录取的10名研究生与10名导师之间做双向选择,即学生可根据自己的专业发展意愿(依次申报2个专业志愿)、导师的基本情况和导师对学生的期望要求来选择导师;导师根据学生所报专业志愿、专家组对学生专长的评价和自己对学生的期望要求等来选择学生。
请你给出一种10名研究生和导师之间的最佳双向选择方案(并不要求一名导师只带一名研究生),使师生双方的满意度最大。
(2) 根据上面已录取的10名研究生的专业志愿,如果每一位导师只能带一名研究生,请你给出一种10名导师与10名研究生双向选择的最佳方案,使得师生双方尽量都满意。
(3) 如果由十位导师根据初试的成绩及专家组的面试评价和他们自己对学生的要求条件录取研究生,那么,10名研究生的新录取方案是什么?为简化问题,假设没有申报专业志愿,请你给出这10名研究生各申报一名导师的策略和导师各选择一名研究生的策略。
相互选中的即为确定;对于剩下的导师和学生,再按上述办法进行双向选择,直至确定出每一名导师带一名研究生的方案,使师生都尽量满意。
(4) 学校在确定研究生导师的过程中,要充分考虑学生的申报志愿情况。
为此,学校要求根据10名导师和15名学生的综合情况选择5名导师招收研究生,再让这5名导师在
15名学生中择优录取10名研究生。
请你给出一种导师和研究生的选择(录取)方案,以及每一名导师带2名研究生的双向选择最佳策略。
(5) 请你设计一种更能体现“双向选择”的研究生录取方案,提供给主管部门参考,并说明你的方案的优越性。
二模型的假设
为简化问题根据实际情况,提出如下假设。
、:
1 学生在衡量自己与导师期望要求之间的差异时,用的是专家组对自己的评分表数据,而不是自我评价的数值。
2 假设专家对学生的评价公平合理,且每位专家对学生的评价都是同等重要的,并且每个方面的评价也是同等重要的。
3 如果不特殊指明,研究生初试成绩所占比重为α=0.7,导师对学生的客观成绩的偏重系数β=0.7,学生对导师学术水平的偏重系数μ=0.7,学生对导师平均满意度的偏重系数为ω=0.5。
三符号说明
100
⨯=N
x n i
四 模型的分析与建立
研究生录取问题和公司人力资源配置问题非常类似,都是通过双向选择更好
地优化组织的人员结构,提高组织的整体效能。
但由于在实际操作中尚缺乏科学, 可行的方法,往往达不到理想的效果。
我们知道,组织是一个多因素,多层次的 人造系统,是由许多相互作用相互依存的要素组成的有机整体,要使它形成一个 合理、有效的结构,必须将人员配置的方法建立在对构成组织的相关要素进行综 合、系统分析和客观评价的基础上。
考虑到组织的人员结构是不同素质、不同能力的人在组织内各岗位上的分布 状态。
我们建模的思路是,以提高组织的整体效能(师生双方总的满意度)为目 标,通过对学生、导师进行定量测评和综合分析,建立一个系统优化模型,以此 寻求学生和导师之间的最佳对应,实现招生调剂的优化。
以下就方法和模型的建立分步阐述:
第一步:对笔试成绩和面试成绩进行量化处理百分制表示为x ,笔试成绩总分以N=500计,第i 个学生的笔试成绩用n i 表示
,公式为
A 、
B 、
C 、
D 量化为具体的数字,对应法则是A = 95、B = 85、C = 75、D = 65,求
出八位专家对每位学生五项指标的考核的数学期望。
对灵活性、创造性、知识面、表达
力、外语依次编号为1、2、3、4、5(用j 表示)
用Z ij 表示第i 个学生第j 项的分数,用z ij 表示八位专家的综合评分。
公式为
∑=Z z ij ij
81
,以学
生1的灵活性为例得出的综合评分为92.5,则A 为他的最终等级。
第二步用0-1 规划模型进行学生和导师之间的双向选择。
基于上述论述,由于双向选择需要考虑学生对老师满意程度和老师对学生满
意程度的加权和,而学生对老师的满意度又需要考虑对老师专业方向、学术水平 及对学生的期望要求三方面因素满意度的加权和,等等。
故各类因素间的权值定 量就显得非常重要了。
基于Saaty 提出的AHP 法,我们可以对三个以上因素之间的权值进行计算, 即对它们之间的正互反矩阵进行“一致性检验—修正”,保证最终计算出来的权 值更加合理,客观。
而对两个因素之间的权值分配,由于1,2 阶的正互反矩阵 总是一致阵,故权值分配就比较随意,取决于我们对两个因素影响度大小的主观 判断。
第五步模型的实现与求解问题一的解法:
经过分析可知:
8 位专家对学生评价汇总如下:
问题二
考虑10 名学生已经定下来了,在这个条件下,先求出学生对导师的满意度
W ij ,其中根据题意,这个满意度取决于三个方面。
一为学生i与导师j专业匹配
满意度m ij ;二为学生i对导师j水平的满意度g ij ,这项理解为学生通过导师发文、检索、著书、课题等素质的加权,权值根据一致性检验修正定为
1,1.5,3.5,4
三为学生i 与导师j期望要求匹配满意度r ij ,这项理解为用学生复试时5 项
素质的档次去和老师在这个方面的要求进行比较,高出一档加1 分、两档加3 分、三档加6 分,低一档减1 分、两档减3 分、三档减6 分,最后加权求和得到
r ij 。
在这5 项之间的权值选取上,我们选取的初始权值由10 个导师对该项素质
的平均期望要求得到,
为0.89,0.9,0.9,0.84,0.87
经过一致性检验修正,得到最终权值为:
0.213,0.205,0.187,0.203,0.192
可以看出基本上是求平均,略有差异
学生对老师的满意度按下式计算:
SST ij = Wm ij ×m ij + Wg ij ×g ij + Wr ij ×r ij
我们直接选取Wm ij = 0.6 , Wg ij = 0.3, Wr ij = 0.1,
这么选取的原因是由于Wm ij = 0.6 , Wg ij = 0.3, Wr ij = 0.1能通过一致性检验
事实上,
0.1
0.6
0.3
0.6
0.1
0.3 × = 满足正互反矩阵的一致性必要条件。
用同样的方法计算10 位导师对10 名学生的满意度ji W ,根据题意,这个满
意度同样也取决于三个方面。
一为导师j对学生i专业意愿满意度m ji ,二是专
家组对学生专长的评价,即学生自身在面试中的综合表现g ji ,三是导师j对学
生i期望要求满意度r ji 。
导师对学生的满意度按下式计算:
SST ij = Wm ji ×m ji + Wg ji ×g ji + Wr ji ×r ji。
