河南省各地市高考数学最新联考试题分类汇编14统计

合集下载

河南省普高联考2022-2023学年高三下学期测评(四)理科数学试题PDF版含解析

河南省普高联考2022-2023学年高三下学期测评（四）理科数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知集合，，则（）{24}A xx =<<∣{(6)(3)0}B x x x =--≥∣A ．B ．C ．D ．2A B∈ 3A B∈⋂4A B∈ 5A B∈ 2．若复数z 的共轭复数为，且，则z 的虚部为（）z (2i)35i z z -+=-+A ．B ．C ．D ．22i-2i2-3．已知等比数列的前n 项和为，且，，则（）{}n a n S 123nn S m =⨯-m ∈R 4S =A ．B ．5C ．D ．1331732234．塔是一种在亚洲常见的，有着特定的形式和风格的中国传统建筑．最初是供奉或收藏佛骨、佛像、佛经、僧人遗体等的高耸型点式建筑，称“佛塔”．如图，为测量某塔的总高度AB ，选取与塔底B 在同一水平面内的两个测量基点C 与D ，现测得，，米，在C 点测得塔顶A 的仰角为60°，则塔的总30BCD ∠=︒45BDC ∠=︒30CD =高度约为（））1.4≈ 1.7≈A ．13米B ．24米C ．39米D ．45米5．函数的大致图象是（）3sin ||x xy x -=A ．B ．C ．D．6．某学校为落实“双减”政策，在课后服务时间开展了“绘画、书法、围棋、舞蹈、武术”五项兴趣拓展活动，小明计划从这五项活动中选择三项，则书法、舞蹈这两项活动至多有一项被选中的概率为（）A ．B ．C ．D ．0.90.70.60.37．记不等式组的解集为D ，现有下面四个命题：30,10,30x y x y x -+≤⎧⎪++≤⎨⎪+≥⎩，；，；1:(,)p x y D ∀∈280x y -+≥2:(,)p x y D ∃∈240x y -+>，；，．3:(,)p x y D ∀∈30x y ++>4:(,)p x y D ∃∈330x y +-≤其中真命题的个数是（）A ．1B ．2C ．3D ．48．已知抛物线的焦点为F ，过点F 的直线与抛物线交于点A ，B ，与2:2(0)C x py p =>抛物线的准线交于点M ，且点A 位于第一象限，F 恰好为AM 的中点，，AF BM λ=()λ∈R 则（）λ=A ．B ．CD32439．任意写出一个正整数，并且按照以下的规律进行变换：如果是个奇数，则下一m m 步变成，如果是个偶数，则下一步变成，无论是怎样一个数字，最终必31+m m 12m m 进入循环圈，这就是数学史上著名的“冰雹猜想”．它可以表示为数列1421→→→（为正整数），，若，则的所有可能{}1:n a a m =m 131,1,2n n n n n a a a a a ++⎧⎪=⎨⎪⎩当为奇数时当为偶数时72a =m 取值之和为（）A ．B ．C ．D ．18819019220110．在菱形ABCD 中，，，AC 与BD 的交点为G ，点M ，N 分别在线段5AB =6AC =AD ，CD 上，且，，将沿MN 折叠到，使13AM MD =13CN ND =MND MND '△的外接球的表面积为（）GD '=D ABC '-A ．B ．C ．D ．1203π16627π16289π840π11．设双曲线的左、右焦点分别为，，B 为双曲线E 上:E 22221x y a b-=(0,0)a b >>1F 2F 在第一象限内的点，线段与双曲线E 相交于另一点A ，AB 的中点为M ，且1F B ，若，则双曲线E 的离心率为（）2F M AB ⊥1230AF F ∠=︒AB ．2C D 12．已知，，，其中e 为自然对数的底数，则（）0.618e 1a =-ln1.618b =tan 0.618c =A ．B ．c a b >>a b c >>C ．D ．b a c>>a c b>>二、填空题13．二项式的展开式中的系数为________．523x x ⎛⎫+ ⎪⎝⎭4x 14．如图，在矩形ABCD 中，，AC 与BD 的交点为M ，N 为边AB 上任22AB BC ==意点（包含端点），则的最大值为________．MB DN ⋅15．圆与x 轴交于A ，B 两点(A 在B 的左侧)，点N 满足22:280M x y x ++-=，直线与圆M 和点N 的轨迹同时相切，则直线l 的斜率为||2||NA NB =:(0)l y kx m k =+>________．16．先将函数的图象向左平移个单位长度，再将所得图象上所有点的横()cos f x x =2π3坐标变为原来的，纵坐标不变，所得图象与函数的图象关于x 轴对称，1(0)ωω>()g x 若函数在上恰有两个零点，且在上单调递增，则的取值范围是()g x 2π0,3⎡⎤⎢⎥⎣⎦ππ,1212⎡⎤-⎢⎥⎣⎦ω________．三、解答题17．在中，角A ，B ，C 的对边分别为a ，b ，c ．ABC cos )sin b a C c A -=(1)求A ；(2)若D 在线段AC 上，且，求BD 的最小值．ABC 13AD AC =18．如图，在四棱锥中，底面ABCD 是平行四边形，，M ABCD -4AB =AD =，点M 在底面ABCD 上的射影为CD 的中点O ，E 为线段AD MC ==45ADC ∠︒上的点(含端点)．(1)若E 为线段AD 的中点，证明：平面平面MAD ；MOE ⊥(2)若，求二面角的余弦值．3AE DE =D ME O --19．某公司为了解年营销费用x （单位：万元）对年销售量y （单位：万件）的影响，统计了近5年的年营销费用和年销售量，得到的散点图如图所示，对i x (1,2,3,4,5)i y i =数据进行初步处理后，得到一些统计量的值如下表所示．51ii u=∑51ii v=∑()()51iii u u v v =--∑()521ii u u =-∑16.1026.020.40 1.60表中，，，．已知可以作为年销售量y 关ln i i u x =ln i i v y =5115i i u u ==∑5115i i v v ==∑b y a x =⋅于年营销费用x 的回归方程．(1)求y 关于x 的回归方程；(2)若公司每件产品的销售利润为4元，固定成本为每年120万元，用所求的回归方程估计该公司每年投入多少营销费用，才能使得该产品一年的收益达到最大？（收益销售=利润营销费用固定成本）--参考数据：．4.399e 81≈139≈参考公式：对于一组数据，其回归直线的斜率和截()()()1122,,,,,,n n u v u v u v v u αβ=+距的最小二乘估计分别为，．()()()`121ˆniii ni i u u v v u u β==--=-∑∑ˆˆv u αβ=-20．已知椭圆的右焦点为F ，离心率为，且点在㮋圆上．2222:1(0)x y C a b a b+=>>1231,2⎛⎫ ⎪⎝⎭(1)求椭圆C 的标准方程；(2)过右焦点F 且斜率不为0的直线l 与椭圆C 交于A ，B 两点，线段AB 的中点为Q ，经过坐标原点O 和点Q 的直线m 与椭圆C 交于M ，N 两点，求四边形AMBN 的面积的取值范围．21．已知函数．()2cos sin ()f x mx mx x x m =--∈R (1)当时，求在点处的切线方程；1m =()f x ()()π,πf (2)当时，，求实数m 的取值范围．0x >()0f x >22．在直角坐标系中，直线l 的参数方程为其中t 为参数，以坐标原点为xOy 1,1,x t y t =+⎧⎨=-⎩极点，x 轴非负半轴为极轴建立极坐标系，曲线C 的极坐标方程为，其中为参数．2|sin |2|cos |ρθθ=+θ(1)求直线l 的普通方程和曲线C 的直角坐标方程，并画出曲线C 的简图（无需写出作图过程）；(2)直线与曲线C 相交于A ，B 两点，且的值．:m θα=π0,2α⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭||AB =α23．已知函数的最小值为m ．()2|1||1|4f x x x =++--(1)在直角坐标系中画出的图象，并求出m 的值；()y f x =(2)a ，b ，c 均为正数，且，求的最小值．1a b c m ++=-+222a b c b c a++参考答案：1．B【分析】根据二次不等式解法求出集合B ，求出及，根据元素和集合的关系即A B ⋂A B ⋃可逐项判断.【详解】由题可知或，则，或{6B xx =≥∣3}x ≤{23}A B x x ⋂=<≤∣{4A B x x ⋃=<∣，依据选项可知B 正确.6}x ≥故选：B ．2．D【分析】先根据条件求出复数，然后可得虚部.z 【详解】设复数，a ，，则，i z a b =+b ∈R i (2i)(i)a b a b +-+-()(3)i a b b a =-++-35i =-+即，解得，则，故z 的虚部为2.()335a b b a -+=-⎧⎨-=⎩12a b =⎧⎨=⎩12z i =+故选：D ．3．B【分析】先根据的定义依次求出，再由等比数列的定义即可得到关于的关系式，n S 123,,a a a m 解之即可得出答案.【详解】因为，123nn S m =⨯-当时，，1n =1123a S m ==-当时，，则，2n =21243m a S a =+=-223a =当时，，则，3n =312383a m a a S +=+-=343a =因为是等比数列，所以，则，{}n a 322a q a ==2113a a q ==所以，解得，2133m -=13m =则，11233n n S =⨯-则.45S =故选：B.4．C【分析】在Rt △ABC 根据∠ACB 的正切得AB 与BC 的关系，在△BCD 中利用正弦定理列式即可求解．【详解】设，则，AB m=tan 60m BC ==︒在中，，由正弦定理得，BCD △105CBD ∠=︒sin105sin 45CD BC=︒︒因为，()sin105sin 4560︒=︒+︒sin 45cos 60cos 45sin 60=︒︒+︒︒=代入数据，解得（米），90m =-9030 1.739≈-⨯=故选：C ．5．A【分析】先判断函数的奇偶性即可排除选项；再利用特殊值即可排除选项，进而求解.B,D C 【详解】函数的定义域为，3sin ()xx xy f x -==(,0)(0,)-∞+∞ 且，3sin()3sin ()()x x x xf x x x f x-----+-===-所以是奇函数，图象关于原点对称，排除选项，()f x B,D 只需研究的图象，当时，，则，排除选项.0x >π6x =πππ33sin 06662-=-<π06f ⎛⎫< ⎪⎝⎭C 故选：．A 6．B【分析】方法一：根据排列组合结合分类加法法则得出答案；方法二：先求出“书法、舞蹈这两项活动都被选中”的概率，即可根据对立事件的概率求法得出答案.【详解】方法一：“书法、舞蹈这两项活动至多有一项被选中”分两种情况：①都没有被选中，有种情况；②两项活动只有一项被选中，有种情况，33C 1223C C 则所求概率为，故选B ．31232335C C C 70.7C 10P +===方法二：“书法、舞蹈这两项活动至多有一项被选中”的对立事件是“书法、舞蹈这两项活动都被选中”，故所求概率为，123235C C 710.7C 10P =-==故选：B ．7．C【分析】作出不等式组所表示的区域，再逐项的作出对应直线，观察所作直线与可行域的关系，再利用存在命题与全称命题的概念进行判断即可求解.【详解】不等式组的解集D 表示的可行域如图中阴影部分所示，依据图（1）知命题为真1p 命题，依据图（2）知命题为真命题，2p 依据图（3）知命题为假命题，依据图（4）知命题为真命题．所以真命题有3个，3p 4p故选：C ．8．A【分析】过点A ，B 分别作准线的垂线，垂足分别为N ，E ，根据抛物线的定义，又F 恰好为AM 的中点，可得到比例，进一步推导得到的值.||||AF BM λ【详解】如图，过点A ，B 分别作准线的垂线，垂足分别为N ，E ，根据抛物线的定义得，，||||AF AN =||||BF BE =因为F 为AM 的中点，所以，又||||||||1||||||AF BF BM BF BM BM BM +==+||||||||BF BE BM BM ==，所以，所以.||||1||||2AN AF AM AM ==||||1311||||22AF BF BM BM =+=+=32λ=故选：A 9．B【分析】列举出的可能情况，可得出的所有可能取值，1234567a a a a a a a →→→→→→m 相加即可得解.【详解】由题意，的可能情况有：1234567a a a a a a a →→→→→→①；②；2142142→→→→→→16842142→→→→→→③；④；2010516842→→→→→→310516842→→→→→→⑤；⑥；128643216842→→→→→→21643216842→→→→→→所以，的可能取值集合为，的所有可能取值之和为m {}2,16,20,3,128,21m .21620312821190+++++=故选：B.10．B【分析】设MN 与BD 的交点为H ，连接，证明平面ABC ．设的外接圆圆D H 'D G '⊥ABC 心为，的外接圆圆心为，过，分别作平面ABC ，平面的垂线，设1O AD C ' 2O 1O 2O AD C '两垂线交于点O ，则O 是三棱锥外接球的球心，先求出，再求出三棱锥D ABC '-12,r r 的外接球的半径即得解.D ABC '-R 【详解】如图所示，因为，，13AM MD =13CN ND =所以，设MN 与BD 的交点为H ，连接，//MN AC 'D H 因为，，所以，则，，5AD CD AB ===3GA GC ==4DG =1GH =3DH =所以．又，则．又，3D H '=GD '=222D G GH D H ''+=D G GH '⊥D G AC '⊥，平面ABC ，故平面ABC ．AC HG G ⋂=AC HG ⊂，D G '⊥设的外接圆圆心为，的外接圆圆心为，过，分别作平面ABC ，平ABC 1O AD C ' 2O 1O 2O 面的垂线，设两垂线交于点O ，则O 是三棱锥外接球的球心，且四边形AD C 'D ABC '-为矩形．设的外接圆半径为，在中，由，解得12O OO G ABC 1r ABC ()2221143r r -+=，同理可得的外接圆半径的1258r =AD C ' 2r =2GO =D ABC '-外接球半径为R ，则，则三棱锥的外接球的表面22212R O A GO =+6252627646464=+=D ABC '-积.26274π16S R π==故选：B ．11．D【分析】连结连接、.设，根据双曲线的定义可推得，即2AF 2BF 2AF =2BF m =||4AB a =．进而在直角三角形中，根据勾股定理可得.结合已知条件，即可2m a =2F 得出，从而得出离心率.222c a =【详解】如图，连接、.2AF 2BF 因为M 为AB 的中点，，所以．2F M AB ⊥22AF BF =设，2AF =2BF m =因为，所以.212AF AF a -=12AF m a =-又因为，所以，122B F B F a -=1BF =2m a +则．11||4AB BF AF a =-=因为M 为AB 的中点，所以，则．||||2AM BM a ==1F M m =设，在中，122FF c =12Rt F F M △2F在中，2Rt AF M△2F ，整理可得，所以．=22222m a c =+2F 当时，，则，1230AF F ∠=︒12sin AF F ∠=212FMF F =12=222c a =所以离心率为ce a==故选：D ．12．D【分析】构造函数，，利用导数判断其单调性即可判断的大()1tan x f x x =--e π04x <<,a c 小；，可构造函数判断与的大小，ln1.618ln(10.618)b ==+()ln(1)h x x x =+-ln1.618b =0.618构造函数判断与的大小，从而可判断的大小.()tan k x x x =-0.618tan 0.618,b c 【详解】令，，()1tan xf x x =--e e cos cos sin cos x x x xx--=π04x <<令，()e cos x g x x =-cos sin x x -则，()(sin cos )e x g x x x '=-+sin cos x x +-()e 1(cos sin )xx x =--当时，，则在上单调递增，π04x <<()0g x '>()g x 0,4π⎛⎫⎪⎝⎭又，所以当时，，又，所以在上恒(0)110g =-=04x π<<()0g x >cos 0x >()0f x >0,4π⎛⎫⎪⎝⎭成立，又，所以，即．00.6184π<<(0.618)0f >a c >令，则，()ln(1)h x x x =+-1()111x h x x x -=-=++'当时，，所以在上单调递减，02x π<<()0h x '<()h x 0,2π⎛⎫⎪⎝⎭所以当时，，即．02x π<<()(0)0h x h <=ln(1)x x +<令，则，在上单调递减，()tan k x x x =-21()10cos k x x '=-≤()k x 0,2π⎛⎫⎪⎝⎭所以当时，，即，02x π<<()(0)0k x k <=tan x x <所以在上恒成立．ln(1)tan x x x +<<0,2π⎛⎫⎪⎝⎭令，则，所以．0.618x =ln(0.6181)0.618tan 0.618+<<c b >综上所述，．a c b >>故选：D ．【点睛】构造函数比较大小主要方法有：1.通过找中间值比较大小，要比较的两个或者三个数之间没有明显的联系，这个时候我们就可以通过引入一个常数作为过渡变量，把要比较的数和中间变量比较大小，从而找到他们之间的大小；2.通过构造函数比较大小，要比较大小的几个数之间可以看成某个函数对应的函数值，我们只要构造出函数，然后找到这个函数的单调性，就可以通过自变量的大小关系，进而找到要比较的数的大小关系.有些时候构造的函数还需要通过放缩法进一步缩小范围.13．90【分析】由二项式展开式通项公式可求.【详解】由题知，当时，，故的系数为90．()52153C rrrr T xx -+⎛⎫= ⎪⎝⎭1035C 3r r rx -=⋅⋅2r =4390T x =4x 故答案为：90.14．##522.5【分析】以点A 为坐标原点，，的方向为x 轴，y 轴正方向建立平面直角坐标系，写ABAD 出对应点的坐标，设，根据平面向量数量积的坐标运算即可求解.(,0)N m (02)m ≤≤【详解】以点A 为坐标原点，，的方向为x 轴，y 轴正方向，建立平面直角坐标系，ABAD 则，，，设，11,2M ⎛⎫⎪⎝⎭(2,0)B (0,1)D (,0)N m (02)m ≤≤所以，，则，11,2MB ⎛⎫=- ⎪⎝⎭ (,1)DN m =- MB DN ⋅= 12m +因为，所以，即的最大值为．02m ≤≤1522MB DN ≤⋅≤ MB DN ⋅ 52故答案为：．5215【分析】求出A 、B 坐标，设N (x ,y )，求出N 的轨迹圆E 的方程，作出图象，利用圆的公切线的几何性质即可求其斜率．【详解】对于圆，令，得，解得或，22:280M x y x ++-=0y =2280x x +-=4x =-2x =则，．()4,0A -()2,0B 设，∵，∴，(,)N x y 2NANB=2NA NB =，整理得，=22(4)16x y -+=则点N 的轨迹是圆心为，半径为的圆．()4,0E 4R =又圆M 的方程为，则圆M 的圆心为，半径为．22(1)9x y ++=(1,0)-3r =∵，∴两圆相交，434(1)43-<--<+设直线l 与圆M 和点N 轨迹圆E 切点分别为C ，D ，连接CM ，DE ，过M 作DE 的垂线，垂足为点F ，则四边形CDFM 为矩形，∵，，∴5ME =431EF DE DF R CM =-=-=-=MF =则tan FME ∠则两圆公切线CD 的斜率即为直线FM16．11,44⎡⎤⎢⎥⎣⎦【分析】先根据题目的要求平移伸缩对称变换得到的解析式，然后结合函数在()g x 2π0,3⎡⎤⎢⎥⎣⎦上恰有两个零点以及在上单调递增，列出不等式组，即可求得本题答案.ππ,1212⎡⎤-⎢⎥⎣⎦【详解】函数的图象向左平移个单位长度，得到的图象，()f x 2π32πcos 3y x ⎛⎫=+ ⎪⎝⎭再将图象上所有点的横坐标变为原来的，纵坐标不变，得到的图象，因1ω2πcos 3y x ω⎛⎫=+ ⎪⎝⎭为函数的图象与的图象关于x 轴对称，()g x 2πcos 3y x ω⎛⎫=+ ⎪⎝⎭所以，2π()cos 3g x x ω⎛⎫=-+ ⎪⎝⎭2ππsin 32x ω⎛⎫=+-= ⎪⎝⎭πsin 6x ω⎛⎫+ ⎪⎝⎭因为，所以，20π3x ≤≤ππ2ππ6636x ωω≤+≤+又因为在恰有2个零点，且，，π()sin 6g x x ω⎛⎫=+ ⎪⎝⎭2π0,3⎡⎤⎢⎥⎣⎦()sin π0k =Z k ∈所以，解得，2π2ππ3π36ω≤+<1117<44ω≤令，，得，，令，22πππ2π2π262k x k ω-+≤+≤+2k ∈Z 222π2π2ππ33k k x ωωωω-+≤≤+2k ∈Z 20k =得在上单调递增，所以，()g x 2ππ,33ωω⎡⎤-⎢⎥⎣⎦ππ,1212⎡⎤-⎢⎥⎣⎦2ππ,33ωω⎡⎤⊆-⎢⎥⎣⎦所以，又，解得．2ππ312ππ312ωω⎧-≤-⎪⎪⎨⎪≥⎪⎩0ω>04ω<≤综上所述，，故的取值范围是．1144ω≤≤ω11,44⎡⎤⎢⎥⎣⎦故答案为：11,44⎡⎤⎢⎥⎣⎦17．(1)；π3A =【分析】（1）根据正弦定理，结合三角恒等变换化简可推得tan A =（2）由已知可推得.在中，由余弦定理可推得，然后根据9bc =ABD △2221193c bbc BD =+-基本不等式，即可得出BD 的最小值．【详解】（1，sin cos )sin sin B A CC A -=又，πA B C ++=]sin()sin cossin sin A C A C C A +-=．sin A C sin sin C A =又，则．sin 0C >sin A A =tan A =因为，所以．(0,π)A ∈π3A =（2）由（1）知，则的面积为．π3A =ABC 1πsin 23S bc ===9bc =在中，，ABD △13AD b =由余弦定理得2222cos BD AB AD AB AD A =+-⋅2211π2cos933c b c b =+-⨯⨯⨯，221193c b bc =+-≥13bc 133bc ==当且仅当，即2219c b =b =c =所以BD 18．(1)证明见解析【分析】(1)在△ADO 中，利用勾股定理证明ED ⊥EO ，再结合ED ⊥MO 即可证明平面MOE ，AD ⊥从而可证明平面平面MAD ；MOE ⊥(2)连接OA ，证明，以O 为坐标原点，建立空间直角坐标系，利用空间向量即可DO OA ⊥求解二面角的余弦值．【详解】（1）∵平面ABCD ，平面ABCD ，∴．AD ⊂MO ⊥MO AD ⊥∵O 为线段CD 的中点，E 为线段AD 的中点，∴，2DO =DE =∵，由余弦定理得，=45ADC ∠︒2222222EO =+-⨯=则，则．222EO DE DO +=DE EO ⊥∵，平面MOE ，∴平面MOE ，MO EO O ⋂=,MO EO ⊂AD ⊥又∵平面MAD ，∴平面平面MAD ．AD ⊂MOE ⊥（2）连接OA ，由(1)知当E 为线段AD 的中点时，AE DE EO ===则A 、O 、D 三点在以AD 为直径的圆上，故．DO OA ⊥故以O 为原点，建立如图所示的空间直角坐标系，又，MC =2MO =∴，，，．(0,0,0)O (2,0,0)D (0,2,0)A (0,0,2)M 又，则，3AE DE =13,,022E ⎛⎫⎪⎝⎭∴，，，．(0,0,2)OM = (2,0,2)DM =- (2,2,0)DA =-13,,022OE ⎛⎫= ⎪⎝⎭设平面MAD 的法向量为，则解得()111,,m x y z = 1111220220DM m x z DA m x y ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩ ，，1111x z x y =⎧⎨=⎩，，取，则平面MAD 的一个法向量为．11x =(1,1,1)m =设平面MEO 的法向量为，则解得()222,,x n y z = 2221302220OE n x y OM n z ⎧⋅=+=⎪⎨⎪⋅==⎩，，22230x y z =-⎧⎨=⎩，，取，则平面MEO 的一个法向量为．23x =(3,1,0)n =-则，cos m n m n m n ⋅⋅===⋅则二面角D ME O --19．(1)1481y x =(2)该公司每年投入351万元营销费用时，该产品一年的收益达到最大【分析】(1)根据题目要求可知，y 关于x 的回归方程为非线性的，设，可得b y a x =⋅，代入已知条件所给的数据，计算即可.(2)列出年收益与营销费用的关系式，ln ln ln y a b x =+通过求导来求得最值.【详解】（1）由得，，令，，，则b y a x =⋅ln ln()ln ln b y a x a b x =⋅=+ln u x =ln v y =lnc a =．v c bu =+由表中数据可得，，()()()515210.4ˆ0.251.6iii ii u u v v bu u ==--===-∑∑则，所以．26.0216.1ˆˆ0.25 4.39955cv bu =-=-⨯=ˆ 4.3990.25v u =+即，因为，所以，ˆln 4.3990.25ln y x =+14.3994ln e x ⎛⎫=⋅ ⎪⎝⎭ 4.399e 81≈14ˆ81y x =故所求的回归方程为．1481y x =（2）设年收益为W 万元，则，144120324120W y x x x =--=--对求导，得，()W f x =34'()811f x x -=-令，解得，348110x --=132433519x =≈⨯=当时，，单调递增，当时，，单调递减，(0,351)x ∈'()0f x >()f x (351,)x ∈+∞'()0f x <()f x 因此，当时W 有最大值，即该公司每年投入351万元营销费用时，该产品一年的收351x =益达到最大．20．(1)；22143xy +=(2)．[6,【分析】（1）由题得到关于的方程，解方程即得解；,,a b c （2）设直线l 的方程为，联立椭圆C 的方程得到韦达定理，设线段AB 的中点为1x ky =+，求出它的坐标，求出、点M ，N 到直线l 的距离，再化简求出()00,Q x y ||AB 12,d d 即得解.S =【详解】（1）设椭圆右焦点的坐标为，则，即，(,0)(0)c c >12c a =2a c =又，则，222a b c =+223b c =因为点在椭圆上，31,2⎛⎫ ⎪⎝⎭所以，即，解得，221914a b +=2213144c c +=1c =则，C 的标准方程为．2a =b =22143x y +=（2）由（1）知，因为直线l 的斜率不为0，所以可设直线l 的方程为，(1,0)F 1x ky =+代入椭圆C 的方程，消去x 化简得，22143x y +=()2234690k y ky ++-=设，，则，．()11,A x y ()22,B x y 122634ky y k -+=+122934y y k -=+设线段AB 的中点为，则，，()00,Q x y 12023234y y k y k +-==+200231134k x ky k -=+=++2434k =+即，则直线m 的方程为，2243,3434k Q k k -⎛⎫ ⎪++⎝⎭34k y x =-代入椭圆C 的方程可得，x =M．N⎛ ⎝||AB =-=，=()2212134k k +=+点M ，N 到直线l 的距离分别为1d 2d 则四边形AMBN 的面积为1211||||22S AB d AB d =⨯⨯+⨯⨯()121|2ABd d =⨯⨯+∣1||2AB =⨯⨯因为点M ，N 在直线l 的两侧，所以1|2S AB =⨯1||2AB ⨯⨯1||2AB ⨯()221211234k k +=⨯+=，==因为，所以2110344k <≤+6S ≤<因此，四边形AMBN 的面积的取值范围为．[6,21．(1)4πy x =-(2)[1,)+∞【分析】（1）由导数法求切线；（2）法一：对m 分类讨论，由导数法研究函数单调性及符号即可判断，其中时，由作1m ≥差法说明，将问题转化为判断的符号；()2cos sin f x x x x x ≥--()2cos sin g x x x x x =--法二：不等式等价为，由导数法研究图象性质，由数形结合判sin 2cos xmx x >-sin ()2cos x g x x=-断范围.【详解】（1）因为，所以，()2cos sin f x x x x x =--()22cos sin f x x x x '=-+因为，，所以切线方程为，即．()π4f '=()π3πf =()3π4πy x -=-4y x π=-（2）方法一：i.若，1m ≥由，2cos sin (2cos sin )mx mx x x x x x x -----2(1)(1)cos m x m x x =---(1)(2cos )0m x x =--≥可得，()2cos sin f x x x x x ≥--设，则，()2cos sin g x x x x x =--()22cos sin g x x x x '=-+当时，，所以单调递增，则；(0,]x π∈()0g x '>()g x ()(0)0g x g >=当时，，所以，(,)x ∈π+∞()(1cos )(sin )0g x x x x x =-+->()0g x >所以恒成立，符合题意；()0f x >ii.若，，0m ≤()2cos sin f x mx mx x x =--(1cos )sin mx x mx x =-+-当时，，不合题意．π0,2x ⎛⎫∈ ⎪⎝⎭()0f x <iii.若，，01m <<()2(1)cos sin f x m m x mx x '=-++设，则，()()h x f x '=()(21)sin cos h x m x mx x '=++当时，，所以在上单调递增，π0,2x ⎛⎫∈ ⎪⎝⎭()0h x '>()f x 'π0,2⎛⎫ ⎪⎝⎭因为，，所以存在，使得，ππ2022f m ⎛⎫⎛⎫=+> ⎪ ⎪⎝⎭⎝⎭'(0)0f '<0π0,2x ⎛⎫∈ ⎪⎝⎭()00f x '=当时，，则在上单调递减，，不合题意．()00,x x ∈()0f x '<()f x ()00,x ()(0)0f x f <=综上所述，m 的取值范围为．[1,)+∞方法二：由题知当时，，即，0m >2cos sin 0mx mx x x -->(2cos )sin mx x x ->因为，所以．2cos 0x ->sin 2cos xmx x>-设，因为，所以为周期函数，且周期为．sin ()2cos x g x x=-(2)()g x g x π+=()g x 2π，22cos (2cos )sin ()(2cos )x x x g x x --'=-22cos 1(2cos )x x -=-令，则或，，()0g x '=π2π3x k =+5π2π3x k =+k ∈Z 所以当，时，，则单调递增；ππ2π,2π33x k k ⎛⎫∈-++ ⎪⎝⎭k ∈Z ()0g x '>()g x 当，时，，则单调递减．π5π2,2π33x k k π⎛⎫∈++ ⎪⎝⎭k ∈Z ()0g x '<()g x 当时，令，则，则单调递减，0,3x π⎛⎫∈ ⎪⎝⎭()()h x g x '=32sin (1cos )()0(2cos )x x h x x -+'=<-()()h x g x '=∴.()(0)1g x g ''<=当时，直线与曲线相切，如图，1m =y mx =()y g x =根据图象可知，要使，只需，故实数m 的取值范围为．sin 2cos x mx x>-m 1≥[1,)+∞【点睛】恒成立问题，一般可通过分离参数法，转化为由导数法研究不含参部分的最值；或者对参数分类讨论，由导数法分别说明.22．(1)，，作图见解析；20x y +-=222||2||0x y x y +--=(2)或．π12α=5π12α=【分析】（1）消去参数，即可得出直线的普通方程.根据公式即可求得曲线C 的直角坐标方t 程.然后根据方程作图即可；（2）设点A 位于第一象限，由图象集合已知条件可推出，2sin 2cos A ραα=+.由.然后根据的范围，即可得出2sin 2cos B ραα=+||AB =πsin 4α⎛⎫+= ⎪⎝⎭αα的值．【详解】（1）将直线的参数方程消去t ，得普通方程为．20x y +-=曲线C 的极坐标方程为，即，2|sin |2|cos |ρθθ=+22|sin |2|cos |ρρθρθ=+又，，，所以曲线C 的直角坐标方程为222x y ρ=+cos x ρθ=sin y ρθ=．222||2||0x y x y +--=则曲线C的简图如图所示．（2）不妨设点A 位于第一象限，结合图形和直线可知，:0,2m πθαα⎛⎫⎡⎤=∈ ⎪⎢⎥⎣⎦⎝⎭，，2sin 2cos A ραα=+2sin(π)2cos(π)B ραα=-+-+2sin 2cos αα=+则，||4sin 4cos A B AB ρραα=+=+π4α⎛⎫=+= ⎪⎝⎭所以.πsin 4α⎛⎫+ ⎪⎝⎭又，所以，π0,2α⎡⎤∈⎢⎥⎣⎦ππ3π,444α+∈⎡⎤⎢⎥⎣⎦则或，所以或．ππ43α+=π2π43α+=π12α=5π12α=23．(1)作图见解析，2m =-(2)3【分析】(1)写出f (x )解析式，按照一次函数图象画法即可画出图象，根据图象即可求出最小值m ；(2)利用基本不等式得，，，三式相加即可求得22a b a b+≥22b c b c +≥22c a c a +≥222a b c b c a ++的最小值．【详解】（1）由题知()35,1,1,11,33,1,x x f x x x x x --≤-⎧⎪=--<<⎨⎪-≥⎩描点，，，，连线得的图象如图所示．(2,1)-(1,2)--(1,0)(2,3)()y f x =通过图象可知，当时，函数的最小值为，即．=1x -()y f x =2-2m =-（2）由(1)知，，2m =-13a b c m ++=-+=，，，22a b a b+≥22b c b c +≥22c a c a +≥三个式子相加得，当且仅当时等式成立，2223a b c a b c b c a++≥++=1a b c ===∴的最小值为3．222a b c b c a++。

2024-2025学年河南省高三上学期联考(二)数学试题及答案

2024-2025年度河南省高三年级联考（二）数学注意事项：1.答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.4.本试卷主要考试内容：集合与常用逻辑用语，函数与导数，三角函数，平面向量，数列，不等式.一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}21A x x =-<，{}3B x a x a =<<+.，若{}15A B x x =<< ，则a =（）A.0B.1C.2D.32.已知符号）（表示不平行，向量(1,2)a =--，(,7)b m m =+ .设命题:(0,)p m ∀∈+∞，a ）（b ，则（）A.:(0,)p m ⌝∃∈+∞，//a b，且p ⌝为真命题B.:(0,)p m ⌝∀∈+∞，//a b，且p ⌝为真命题C.:(0,)p m ⌝∃∈+∞，//a b，且p ⌝为假命题D.:(0,)p m ⌝∀∈+∞，//a b，且p ⌝为假命题3.若||0a b >>，则下列结论一定成立的是（）A.22a b ab > B.2211ab a b> C.33a b < D.a c c b->-4.已知等比数列{}n a 的前n 项和为n S ，且31S ma =，则“7m =”是“{}n a 的公比为2”的（）A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件5.已知函数3()log f x x =，若0b a >>，且a ，b 是()f x 的图像与直线(0)y m m =>的两个交点对应的横坐标，则4a b +的最小值为（）A.2B.4C.6D.86.三角板主要用于几何图形的绘制和角度的测量，在数学、工程制图等领域被广泛应用.如图，这是由两块直角三角板拼出的一个几何图形，其中||||AB AC = ，||||BD BC =，0BD BC ⋅= .连接AD ，若AD x AB y AC =+，则x y -=（）A.1B.2D.327.若0a ≠，()2ππsin 066x ax bx c ⎛⎫-++≥ ⎪⎝⎭对[0,8]x ∈恒成立，则（）A.0a > B.0bc +> C.0c > D.16b c a-=-8.已知A 是函数()e 3xf x x =+图象上的一点，点B 在直线:30l x y --=上，则||AB 的最小值是（）B.3C. D.二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.设数列{}n a ，{}n b 的前n 项和分别为n S ，n T ，且3n an b =，则下列结论不正确的是（）A.若{}n a 是递增数列，则{}n S 是递增数列B.若{}n a 是递减数列，则{}n S 是递减数列C.若{}n a 是递增数列，则{}n T 是递增数列D.若{}n a 是递减数列，则{}n T 是递减数列10.已知(31)f x +为奇函数，(3)1f =，且对任意x ∈R ，都有(2)(4)f x f x +=-，则必有（）A.(11)1f =-B.(23)0f =C.(7)1f =- D.(5)0f =11.已知函数()sin sin 3f x x x =+，则（）A.()f x 的图象关于点(π,0)中心对称B.()f x 的图象关于直线π4x =对称C.()f x的值域为⎡⎢⎣D.()f x 在π3π,24⎡⎤⎢⎥⎣⎦上单调递增三、填空题：本题共3小题，每小题5分，共15分.12.在ABC △中，角A ，B ，C 的对边分别是a ，b ，c ，且1a =，3b =，1cos 3C =，则ABC △外接圆的面积是__________.13.已知某种污染物的浓度C （单位：摩尔/升）与时间t （单位：天）的关系满足指数模型(1)0e k t C C -=，其中0C 是初始浓度（即1t =时该污染物的浓度），k 是常数.第2天（即2t =）测得该污染物的浓度为5摩尔/升，第4天测得该污染物的浓度为15摩尔/升，若第n 天测得该污染物的浓度变为027C ，则n =__________.14.1796年，年仅19岁的高斯发现了正十七边形的尺规作图法.要用尺规作出正十七边形，就要将圆十七等分.高斯墓碑上刻着如图所示的图案.设将圆十七等分后每等份圆弧所对的圆心角为α，则162121tan 2k k α==+∑__________.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.（13分）在ABC △中，角A ，B ，C 的对边分别是a ，b ，c ，4cos 5A =，2cos 3cos a C c A =.（1）求sin C 的值；（2）若3a =，求ABC △的周长.16.（15分）已知函数()sin()(0,0,0π)f x A x b A ωϕωϕ=++>><<的部分图象如图所示.（1）求()f x 的解析式；（2）求()f x 的零点；（3）将()f x 图象上的所有点向右平移π12个单位长度，得到函数()g x 的图象，求()g x 在7π0,12⎡⎤⎢⎥⎣⎦上的值域.17.（15分）已知函数3()33xx a f x ⋅=+，且()()66log 3log 122f f +=.（1）求a 的值；（2）求不等式()22310f x x +->的解集.18.（17分）已知函数2()(2)ln(1)2f x ax x x x =++--.（1）当0a =时，求()f x 的单调区间与极值；（2）当0x ≥时，()0f x ≤恒成立，求a 的取值范围.19.（17分）设数列{}n a 的前n 项和为n S ，若对任意的n +∈N ，都有2n n S kS =（k 为非零常数），则称数列{}n a 为“和等比数列”，其中k 为和公比.（1）若23n a n =-，判断{}n a 是否为“和等比数列”.（2）已知{}n b 是首项为1，公差不为0的等差数列，且{}n b 是“和等比数列”，2n b nc =，数列{}n c 的前n 项和为n T .①求{}n b 的和公比；②求n T ；③若不等式2134(1)22n n n n T m -+->--对任意的n +∈N 恒成立，求m 的取值范围.2024-2025年度河南省高三年级联考（二）数学参考答案1.C 由题意可得{}13A x x =<<.因为{}15A B x x =<< ，所以1,35a a ≥⎧⎨+=⎩，解得2a =.2.A :(0,)p m ⌝∃∈+∞，//a b ，当(7)2m m -+=-，即7m =时，//a b，所以p ⌝为真命题.3.B 当3a =，2b =-时，2218,12a b ab =-=，此时22a b ab <，则A 错误.因为||0a b >>，所以a b >，且0ab ≠，所以2210a b >，所以2211ab a b>，则B 正确.当2a =，1b =-时，338,1a b ==-，此时33a b >，则C 错误.当2a =，1b =，3c =时，1a c -=-，2c b -=，此时a c c b -<-，则D 错误.4.A 设{}n a 的公比为q ，则()23123111S a a a q q a ma =++=++=.因为10a ≠，所以21q q m ++=.由7m =，得217q q ++=，即260q q +-=，解得2q =或3q =-.由2q =，得7m =，则“7m =”是“{}n a 的公比为2”的必要不充分条件.5.B 由题意可得01a b <<<，1b a=，则44a b +≥，当且仅当42a b ==时，等号成立.故4a b +的最小值为4.6.A 如图，以A 为原点，AB ，AC的方向分别为x ，y 轴的正方向，建立直角坐标系，设1AB =，则(0,0)A ，(1,0)B ，(0,1)C ，故(1,0)AB = ，(0,1)AC =.作DF AB ⊥，交AB 的延长线于点F .设||1AB = ，则||||1BF DF ==，所以(2,1)D ，所以(2,1)AD = .因为AD x AB y AC =+，所以2,1x y ==，则1x y -=.7.B 因为[0,8]x ∈，所以πππ7π,6666x ⎡⎤-∈-⎢⎥⎣⎦.当[0,1)x ∈时，ππsin 066x ⎛⎫-< ⎪⎝⎭；当()1,7x ∈时，ππsin 066x ⎛⎫-> ⎪⎝⎭；当(7,8]x ∈时，ππsin 066x ⎛⎫-< ⎪⎝⎭.因为()2ππsin 066x ax bx c ⎛⎫-++≥ ⎪⎝⎭对[0,8]x ∈恒成立，所以1，7是20ax bx c ++=的两根，且0a <，则17,17,b ac a ⎧+=-⎪⎪⎨⎪⨯=⎪⎩故80b a =->，70c a =<，15b c a -=-，0b c a +=->.8.D 由题意可得()(1)e xx f x +'=.设()()g x f x '=，则()(2)e xg x x '=+，当1x <-时，()0f x '<，当1x >-时，()0g x '>，()f x '单调递增.因为(0)1f '=，所以()(1)e 1x f x x '=+=，得0x =，此时(0,3)A，故min ||AB ==.9.ABD 当7n a n =-时，{}n a 是递增数列，此时{}n S 不是递增数列，则A 错误.当12n a n =-+时，{}n a 是递减数列，此时{}n S 不是递减数列，则B 错误.由{}n a 是递增数列，得{}n b 是递增数列，且0n b >，则{}n T 是递增数列，故C 正确.由{}n a 是递减数列，得{}n b 是递减数列，且0n b >，则{}n T 是递增数列，故D 错误.10.CD 由(31)f x +为奇函数，可得(31)(31)f x f x -+=-+，则()f x 的图象关于点(1,0)对称.又(2)(4)f x f x +=-，所以()f x 的图象关于直线3x =对称，则()f x 是以8为周期的周期函数，所以(7)(3)1f f =-=-，(5)(1)0f f ==，(11)(3)1f f ==，(23)(7)1f f ==-，故选CD.11.ACD 因为(π)(π)sin(π)sin 3(π)sin(π)sin 3(π)0f x f x x x x x ++-=++++-+-=，所以()f x 的图象关于点(π,0)中心对称，则A 正确.由题意可得()sin sin 32sin 2cos f x x x x x =+=，则ππππ2sin 2cos 2cos 2cos 4244f x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫+=++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，ππππ2sin 2cos 2cos 2cos 4244f x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫-=--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，所以ππ44f x f x ⎛⎫⎛⎫+≠- ⎪ ⎪⎝⎭⎝⎭，所以()f x 的图象不关于直线π4x =对称，则B 错误.由题意可得3()2sin 2cos 4sin 4sin f x x x x x ==-.设sin [1,1]t x =∈-，则3()44y g t t t ==-+，故()22()124431g t t t '=-+=--.由()0g t '>，得t <<()0g t '<，得1t -≤<1t <≤，则()g t在1,⎡-⎢⎣和⎤⎥⎦上单调递减，在⎛ ⎝上单调递增.因为(1)(1)0g g -==，g ⎛= ⎝，g =()g t ⎡∈⎢⎣，即()f x的值域是⎡⎢⎣，则C 正确.当π3π,24x ⎡⎤∈⎢⎥⎣⎦时，sin t x ⎤=∈⎥⎦.因为sin t x =在π3π,24⎡⎤⎢⎥⎣⎦上单调递减，且()g t在⎤⎥⎦上单调递减，所以()f x 在π3π,24⎡⎤⎢⎥⎣⎦上单调递增，则D 正确.12.9π4 由余弦定理可得22212cos 1921383c a b ab C =+-=+-⨯⨯⨯=，则c =因为1cos 3C =，所以sin C =，则ABC △外接圆的半径32sin 2c R C ==，故ABC 外接圆的面积为29ππ4R =.13.7 由题意可得030e 5,e 15,k kC C ⎧=⎨=⎩则2e 3k =，解得ln 32k =.因为(1)00e 27k n C C -=，即3ln(1)200e 27n C C -=，所以ln 3(1)2e 27n -=，所以ln 3(1)ln 273ln 32n -==，解得7n =.14.15 由题可知2π17α=，则222π11tan 1tan π217cos 17k k k α+=+=，则161616162211112π2π2π2cos 1cos 16cos 1717171tan 2k k k k k k k k α====⎛⎫==+=+ ⎪⎝⎭+∑∑∑∑.由161611π2π(21)π(21)π33πππ2sin cos sin sin sin sin 2sin17171717171717k k k k k ==+-⎡⎤⋅=-=-=-⎢⎥⎣⎦∑∑，得1612πcos117k k ==-∑，故原式16115=-=.15.解：（1）因为4cos 5A =，且0πA <<，所以3sin 5A ==.因为2cos 3cos a C c A =，所以2sin cos 3sin cos A C C A =，所以342cos 3sin 55C C ⨯=⨯，即cos 2sin C C =.因为22sin cos 1C C +=，所以21sin 5C =.因为0πC <<，所以sin C =（2）由（1）可知3sin 5A =，4cos 5A =，sin C =，cos C =，则34sin sin()sin cos cos sin 55B A C A C A C =+=+==由正弦定理可得sin sin sin a b cA B C==，则sin sin a B b A ==，sin sin a C c A==，故ABC △的周长为3a b c ++=+.16.解：（1）由图可知3(1)22A --==，3(1)12b +-==，()f x 的最小正周期7ππ2π1212T ⎛⎫=-= ⎪⎝⎭.因为2π||T ω=，且0ω>，所以2ω=.因为()f x 的图象经过点π,312⎛⎫⎪⎝⎭，所以ππ2sin 2131212f ϕ⎛⎫⎛⎫=⨯++= ⎪ ⎪⎝⎭⎝⎭，即πsin 16ϕ⎛⎫+=⎪⎝⎭，所以ππ2π()62k k ϕ+=+∈Z ，即π2π()3k k ϕ=+∈Z .因为0πϕ<<，所以π3ϕ=.故π()2sin 213f x x ⎛⎫=++ ⎪⎝⎭.（2）令()0f x =，得π1sin 232x ⎛⎫+=- ⎪⎝⎭，则ππ22π()36x k k +=-∈Z 或π5π22π()36x k k +=-∈Z ，解得ππ4x k =-或7ππ()12k k -∈Z ，故()f x 的零点为ππ4k -或7ππ()12k k -∈Z .（3）由题意可得πππ()2sin 212sin 211236g x x x ⎡⎤⎛⎫⎛⎫=-++=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.因为7π0,12x ⎡⎤∈⎢⎥⎣⎦，所以ππ4π2,663x ⎡⎤+∈⎢⎥⎣⎦.当ππ262x +=，即π6x =时，()g x 取得最大值π36g ⎛⎫= ⎪⎝⎭；当π4π263x +=，即7π12x =时，()g x 取得最小值7π112g ⎛⎫= ⎪⎝⎭.故()g x 在7π0,12⎡⎤⎢⎥⎣⎦上的值域为1⎡⎤⎣⎦.17.解：（1）因为3()33x x a f x ⨯=+，所以221393(2)333933x x x xa a af x --+⨯-===+++，则33()(2)3333x x x a af x f x a ⨯+-=+=++.又666log 3log 12log 362+==，所以()()66log 3log 12f f a +=，从而2a =.（2）由（1）可知236()23333x x xf x ⨯==-++，显然()f x 在R 上单调递增.因为1(0)2f =，所以由()22310f x x +->，可得()23(0)f x x f +>，则230x x +>，解得3x <-或0x >，故不等式()22310f x x +->的解集为(,3)(0,)-∞-+∞ .18.解：（1）当0a =时，2()2ln(1)2f x x x x =+--，其定义域为(1,)-+∞，则()222(2)22111x x x x f x x x x x ---+'=--==+++.当(1,0)x ∈-时，()0f x '>，()f x 的单调递增区间为(1,0)-，当(0,)x ∈+∞时，()0f x '<，()f x 的单调递减区间为(0,)+∞，故()f x 的极大值为(0)0f =，无极小值.（2）设1t x =+，[1,)t ∈+∞，2()(2)ln 1g t at a t t =+--+，[1,)t ∈+∞，则2()ln 2at a t t a tg -=+-+'.设()()h t g t '=，则222222()2a a t at a h t t t t --++-'=--=.设2()22m t t at a =-++-，则函数()m t 的图象关于直线4at =对称.①当2a ≤时，()m t 在[1,)+∞上单调递减.因为(1)240m a =-≤，所以2()220m t t at a =-++-≤在[1,)+∞上恒成立，即()0h t '≤在[1,)+∞上恒成立，则()h t 在[1,)+∞上单调递减，即()g t '在[1,)+∞上单调递减，所以()(1)0g t g ''≤=，所以()g t 在[1,)+∞上单调递减，则()(1)0g t g ≤=，即()0f x ≤在[0,)+∞上恒成立，故2a ≤符合题意.②当2a >时，()m t 在[1,)+∞上单调递减或在[1,)+∞上先增后减，因为(1)240m a =->，所以存在01t >，使得()00m t =.当()01,t t ∈时，()0m t >，即()0h t '>，所以()g t '在()01,t 上单调递增.因为(1)0g '=，所以()0g t '>在()01,t 上恒成立，所以()g t 在()01,t 上单调递增，则()0(1)0g t g >=，故2a >不符合题意.综上，a 的取值范围为(,2]-∞.19.解：（1）因为23n a n =-，所以121n a n +=-，所以12n n a a +-=.因为11a =-，所以{}n a 是首项为-1，公差为2的等差数列，则22n S n n =-，所以2244n S n n =-，所以222444422n n S n n n S n n n --==--.因为442n n --不是常数，所以{}n a 不是“和等比数列”.（2）①设等差数列{}n b 的公差为d ，前n 项和为n S ，则21(1)1222n n n d d S nb d n n -⎛⎫=+=+- ⎪⎝⎭，所以222(2)n S dn d n =+-.因为{}n b 是“和等比数列”，所以2n n S kS =，即222(2)22kd kd dn d n n k n ⎛⎫+-=+- ⎪⎝⎭，所以2,22,2kd d kd d k ⎧=⎪⎪⎨⎪-=-⎪⎩解得4,2,k d =⎧⎨=⎩即{}n b 的和公比为4.②由①可知12(1)21n b n n =+-=-，则212n n n c -=，所以35211232222n n n T -=++++ ，所以2352121112122222n n n n nT -+-=++++ ，所以235212121211122311111422222212nn n n n n n T -++⎡⎤⎛⎫⨯-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦=++++-=-- ，即2132344332n n n T ++=-⨯，所以21834992n n n T -+=-⨯.③设2121212134834348103429922992n n n n n n n n n n P T ----++++=-=--=-⨯⨯，12121103710345(1)092924n n n n n n n n P P ++-+++-=-⨯+⨯=>.不等式2134(1)22n n n n T m -+->--对任意的n +∈N 恒成立，即不等式(1)2n n P m >--对任意的n +∈N 恒成立.当n 为奇数时，()1min 23n m P P --<==-，则1m >；当n 为偶数时，()2min 122n m P P -<==-，则32m <.综上，m 的取值范围是31,2⎛⎫⎪⎝⎭.。

河南省开封五县联考2025届高考数学必刷试卷含解析

河南省开封五县联考2025届高考数学必刷试卷注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知定义在R 上的函数||()21x m f x -=-（m 为实数）为偶函数，记()0.5log 3a f =，()2log 5b f =，(2)c f m =+则a ，b ，c 的大小关系为( ) A ．a b c <<B ．a c b <<C ．c a b <<D ．c b a <<2．已知集合2{|1}A x x =<,2{|log 1}B x x =<，则 A ．{|02}A B x x ⋂=<< B ．{|2}A B x x ⋂=< C ．{|2}A B x x ⋃=<D ．{|12}AB x x =-<<3．集合{|20}N A x x B =-≤=，，则A B =（）A ．{}1B ．{}1,2C ．{}0,1D ．{}0,1,24．已知函数f （x ）＝sin 2x +sin 2（x 3π+），则f （x ）的最小值为（） A ．12B ．14C ．34D ．225．已知圆1C ：22(1)(1)1x y -++=，圆2C ：22(4)(5)9x y -+-=，点M 、N 分别是圆1C 、圆2C 上的动点，P 为x 轴上的动点，则PN PM -的最大值是（） A ．254+ B ．9C ．7D ．252+6．函数()sin x y x-=（[),0x π∈-或(]0,x π∈）的图象大致是（） A ． B ． C ． D ．7．我国宋代数学家秦九韶（1202-1261）在《数书九章》（1247）一书中提出“三斜求积术”，即：以少广求之，以小斜幂并大斜幂减中斜幂，余半之，自乘于上；以小斜幂乘大斜幂减上，余四约之，为实；一为从隅，开平方得积. 其实质是根据三角形的三边长a ，b ，c 求三角形面积S ，即2222221[()]42c a b S a c +-=-. 若ABC ∆的面积112S =，3a =，2b =，则sin A 等于（）A ．5510B ．116C ．5510或116D ．1120或11368．已知函数有三个不同的零点（其中），则的值为( )A ．B ．C ．D ．9．已知,x y 满足001x y x y x -⎧⎪+⎨⎪⎩，则32y x --的取值范围为（）A ．3,42⎡⎤⎢⎥⎣⎦B ．(1,2]C ．(,0][2,)-∞+∞D ．(,1)[2,)-∞⋃+∞10．已知函数()3cos (0)f x x x ωωω=->，()y f x =的图象与直线2y =的两个相邻交点的距离等于π，则()f x 的一条对称轴是（）A ．12x π=-B ．12x π=C ．3x π=-D ．3x π=11．定义在R 上的奇函数()f x 满足()()330f x f x --+-=，若()11f =，()22f =-，则()()()()1232020f f f f ++++=（）A ．1-B ．0C ．1D ．212．已知三棱锥P ABC -中，ABC ∆是等边三角形，43,25,AB PA PC PA BC ===⊥，则三棱锥P ABC -的外接球的表面积为（） A ．25πB ．75πC ．80πD ．100π二、填空题：本题共4小题，每小题5分，共20分。

河南省驻马店市(新版)2024高考数学统编版真题(拓展卷)完整试卷

河南省驻马店市（新版）2024高考数学统编版真题(拓展卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题若正数，满足：，则的最大值为（）A．B ．C ．D．2第(2)题在四棱锥中，平面，，底面是菱形，，E ，F ，G 分别是，，的中点，则异面直线与所成角的余弦值为（）A ．B ．C ．D ．第(3)题设函数的图象与函数的图象关于轴对称，将的图象向右平移个单位长度后得到函数的图象，则函数的图象与的图象的所有交点的横坐标之和为（）A ．8B ．6C ．4D ．2第(4)题已知集合，，则（）A ．B ．C ．D ．第(5)题已知双曲线的左焦点为，为坐标原点，为双曲线的右支上一点，若，，则双曲线的离心率为（）A ．B ．C ．D ．第(6)题在黑板上从左到右写2，0，2，3四个数，对两个相邻的数，每次用右边的数减左边的数的差填在这两数中间，从3开始到最左边的2为止，称为填一次.比如填第一次：2，-2，0，2，2，1，3，其中划线部分是填的右边的数减左边的数的差.则这样填2023次之后，黑板上所有数的和是（）A ．2023B ．2025C ．2028D ．2030第(7)题已知和是两个单位向量，若，则向量与向量的夹角为（）A．B ．C ．D ．第(8)题已知函数，，若方程恰有三个不相等的实数根，则实数k 的取值范围是（）A ．B ．C ．D ．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知A ，，，是表面积为20π的球体表面上四点，且，，则（）A ．若，则平行直线与间距离的最大值为3B ．若，则平行直线与间距离的最小值为C ．若A ，，，四点能构成三棱锥，则该三棱锥体积的最大值为4D ．若，则第(2)题下列说法中正确的是（）A．某射击运动员进行射击训练，其中一组训练共射击九次，射击的环数分别为则这组射击训练数据的70分位数为B．已知随机变量服从，若，则C．在经验回归分析中，如果两个变量的相关性越强，则相关系数就越接近于1D．用模型拟合一组数据时，为了求出经验回归方程，设，若通过这样的变换后，所得到经验回归方程为，则第(3)题已知在体能测试中，某校学生的成绩服从正态分布N（70，16），其中60分为及格线，则下列结论中正确的有（）（附：随机变量服从正态分布N（，），则）A．该校学生成绩的均值为70B．该校学生成绩的标准差为4C．该校学生成绩的标准差为16D．该校学生成绩及格率超过95%三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知的展开式中只有第4项的二项式系数最大，且项的系数为，则______．第(2)题已知三行三列的方阵中有9个数a ij（i＝1，2，3；j＝1，2，3），从中任取三个数，则有且仅有两个数位于同行或同列（注意：不能同时出现既有两数同行、又有两数同列的情况）的概率是_____.（结果用分数表示）第(3)题已知椭圆与双曲线共焦点，过椭圆上一点的切线与轴、轴分别交于、两点（、为椭圆的两个焦点）．又为坐标原点，当的面积最小时，下列说法所有正确的序号是__________．①；②当点在第一象限时坐标为；③直线的斜率与切线的斜率之积为定值；④的角平分线（点在上）长为．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知椭圆经过点，且离心率为.(1)求椭圆E的方程和焦点的坐标；(2)设点为椭圆E上的任一点（不在坐标轴上），直线与椭圆E交于另一点为，直线与椭圆E交于另一点为，为坐标原点，证明：直线与的斜率之积为定值.第(2)题已知函数．(1)当时，讨论函数的单调性．(2)若有两个极值点．①求实数的取值范围；②求证：．第(3)题已知等比数列的前项和为，且.(1)求数列的通项公式；(2)在与之间插入个数，使这个数组成一个公差为的等差数列，求证数列的前项和.第(4)题在平面直角坐标系中，过直线上任一点作该直线的垂线，，线段的中垂线与直线交于点．(1)当在直线上运动时，求点的轨迹的方程；(2)过向圆引两条切线，与轨迹的另一个交点分别①判断：直线与圆的位置关系，并说明理由；②求周长的最小值．第(5)题已知椭圆的离心率为，且椭圆过点．(1)求椭圆的标准方程；(2)过右焦点的直线与椭圆交于两点，线段的垂直平分线交直线于点，交直线于点，求的最小值．。

河南省驻马店市(新版)2024高考数学部编版考试(拓展卷)完整试卷

河南省驻马店市（新版）2024高考数学部编版考试(拓展卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题已知函数，的定义域为，且．若是偶函数，，是奇函数，则（）A．B．C．D．第(2)题已知全集，集合，则（）A．B．C．D．第(3)题已知函数，它的两个相邻的极值点之间的距离为．若先将函数的图像向左平移个单位长度，再将其图像上所有点的横坐标伸长为原来的2倍，纵坐标伸长到原来的2倍，得到函数的图像，则在上的零点个数为（）A．4B．5C．6D．8第(4)题已知抛物线的焦点为，该抛物线上一点到的距离为4，则（）A．3B．4C．D．第(5)题棱长为2的正方体内有一个内切球，过正方体中两条异面直线，的中点作直线，则该直线被球面截在球内的线段的长为（）A．B．C．D．1第(6)题已知的二项式系数之和为64，则其展开式的常数项为（）A．B．240C．60D．第(7)题已知向量，若与的夹角为，则（）A．B．C．D．第(8)题在乎面直角坐标系中，O为坐标原点，已知直线，点为圆上两动点，且满足，则到直线的距离之和的最小值为（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知，分别是双曲线（，）的左､右焦点，双曲线左支上存在一点，使（为实半轴长）成立，则此双曲线的离心率的取值可能是（）A．B．2C．D．5第(2)题如图，已知正方体棱长为2，点M为的中点，点P为底面上的动点，则（）A．满足平面的点P的轨迹长度为B．满足的点P的轨迹长度为C．存在点P满足D．以点B为球心，为半径的球面与面的交线长为第(3)题已知的内角的对边分别为，若，则（）A．B．C．D．三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题若实数x、y满足约束条件，则的最小值是______．第(2)题已知数列满足：，，若对任意的正整数均有，则实数的最大值是_____.第(3)题已知函数的两个相邻的零点之差的绝对值为，且是的最小正零点，则__________.四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题所对的内角所对的边分别为，，（1）求的值；（2）若，求的面积第(2)题已知抛物线C：的焦点在圆E：上.(1)设点P是双曲线左支上一动点，过点P作抛物线C的两条切线，切点分别为A，B，证明：直线AB与圆E相切；(2)设点T是圆E上在第一象限内且位于抛物线开口区域以内的一点，直线l是圆E在点T处的切线，若直线l与抛物线C交于M，N两点，求的最大值.第(3)题已知正项数列的前n项和为，且.(1)求数列的通项公式；(2)若，求数列的前n项和.第(4)题中学阶段是学生身体发育最重要的阶段，长时间熬夜学习严重影响学生的身体健康．某校为了解甲、乙两班学生每周自我熬夜学习的总时长（单位：小时），分别从这两个班中随机抽取5名同学进行调查，得到他们最近一周自我熬夜学习的总时长的样本数据：甲班813283239乙班1225262831如果学生平均每周自我熬夜学习的总时长超过26小时，则称为“过度熬夜”．(1)请根据样本数据，分别估计甲、乙两班的学生平均每周自我熬夜学习时长的平均值；(2)从样本甲、乙两班所有“过度熬夜”的学生中任取2人，求这2人都来自甲班的概率．第(5)题已知椭圆E的中心为坐标原点，对称轴为x轴、y轴，且过两点．(1)求E的方程；(2)设过点的直线交E于M，N两点，过M且平行于x轴的直线与线段AB交于点T，点H满足．证明：直线HN过定点．。

历年(2019-2024)全国高考数学真题分类(统计与数字特征)汇编(附答案)

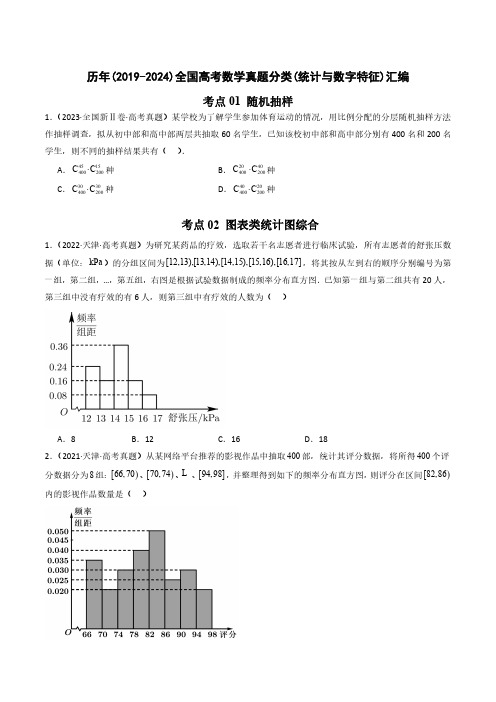
历年(2019-2024)全国高考数学真题分类(统计与数字特征)汇编考点01 随机抽样1．（2023∙全国新Ⅱ卷∙高考真题）某学校为了解学生参加体育运动的情况，用比例分配的分层随机抽样方法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同的抽样结果共有（）．A ．4515400200C C ⋅种B ．2040400200C C ⋅种 C ．3030400200C C ⋅种D ．4020400200C C ⋅种考点02 图表类统计图综合1．（2022∙天津∙高考真题）为研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单位：kPa ）的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17]，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组，右图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为（）A ．8B ．12C ．16D ．182．（2021∙天津∙高考真题）从某网络平台推荐的影视作品中抽取400部，统计其评分数据，将所得400个评分数据分为8组：[)66,70、[)70,74、L 、[]94,98，并整理得到如下的频率分布直方图，则评分在区间[)82,86内的影视作品数量是（）A．20 B．40 C．64 D．804．（2021∙全国甲卷∙高考真题）为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论中不正确的是（）A．该地农户家庭年收入低于4.5万元的农户比率估计为6%B．该地农户家庭年收入不低于10.5万元的农户比率估计为10%C．估计该地农户家庭年收入的平均值不超过6.5万元D．估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间5．（2020∙全国新Ⅱ卷∙高考真题）（多选）我国新冠肺炎疫情进入常态化，各地有序推进复工复产，下面是某地连续11天复工复产指数折线图，下列说法正确的是A．这11天复工指数和复产指数均逐日增加;B．这11天期间，复产指数增量大于复工指数的增量;C．第3天至第11天复工复产指数均超过80%;D．第9天至第11天复产指数增量大于复工指数的增量;5．（2020∙天津∙高考真题）从一批零件中抽取80个，测量其直径（单位：mm），将所得数据分为9组：[)[)[)[]，并整理得到如下频率分布直方图，则在被抽取的零件中，5.31,5.33,5.33,5.35,,5.45,5.47,5.47,5.49直径落在区间[5.43,5.47)内的个数为（）A．10 B．18 C．20 D．36考点03 样本的数字特征一、单选题1．（2024∙全国新Ⅱ卷∙高考真题）某农业研究部门在面积相等的100块稻田上种植一种新型水稻，得到各块稻田的亩产量（单位：kg）并整理如下表亩产[900，950） [950，1000） [1000，1050） [1050，1100） [1100，1150） [1150，1200）量频数 6 12 18 30 24 10根据表中数据，下列结论中正确的是（）A．100块稻田亩产量的中位数小于1050kgB．100块稻田中亩产量低于1100kg的稻田所占比例超过80%C．100块稻田亩产量的极差介于200kg至300kg之间D．100块稻田亩产量的平均值介于900kg至1000kg之间2．（2022∙全国乙卷∙高考真题）分别统计了甲、乙两位同学16周的各周课外体育运动时长（单位：h），得如下茎叶图：则下列结论中错误的是（）A．甲同学周课外体育运动时长的样本中位数为7.4B．乙同学周课外体育运动时长的样本平均数大于8C ．甲同学周课外体育运动时长大于8的概率的估计值大于0.4D ．乙同学周课外体育运动时长大于8的概率的估计值大于0.63．（2022∙全国甲卷∙高考真题）某社区通过公益讲座以普及社区居民的垃圾分类知识．为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如下图：则（）A ．讲座前问卷答题的正确率的中位数小于70%B ．讲座后问卷答题的正确率的平均数大于85%C ．讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差D ．讲座后问卷答题的正确率的极差大于讲座前正确率的极差4．（2020∙全国∙高考真题）在一组样本数据中，1，2，3，4出现的频率分别为1234,,,p p p p ，且411i i p ==∑，则下面四种情形中，对应样本的标准差最大的一组是（）A ．14230.1,0.4p p p p ====B ．14230.4,0.1p p p p ====C ．14230.2,0.3p p p p ====D ．14230.3,0.2p p p p ====5．（2020∙全国∙高考真题）设一组样本数据x 1，x 2，…，xn 的方差为0.01，则数据10x 1，10x 2，…，10xn 的方差为（）A ．0.01B ．0.1C ．1D ．106．（2019∙全国∙高考真题）演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是A ．中位数B ．平均数C ．方差D ．极差二、多选题9．（2023∙全国新Ⅰ卷∙高考真题）有一组样本数据126,,,x x x ⋅⋅⋅，其中1x 是最小值，6x 是最大值，则（） A ．2345,,,x x x x 的平均数等于126,,,x x x ⋅⋅⋅的平均数B ．2345,,,x x x x 的中位数等于126,,,x x x ⋅⋅⋅的中位数C ．2345,,,x x x x 的标准差不小于126,,,x x x ⋅⋅⋅的标准差D ．2345,,,x x x x 的极差不大于126,,,x x x ⋅⋅⋅的极差10．（2021∙全国新Ⅱ卷∙高考真题）下列统计量中，能度量样本12,,,n x x x 的离散程度的是（）A ．样本12,,,n x x x 的标准差B ．样本12,,,n x x x 的中位数C ．样本12,,,n x x x 的极差D ．样本12,,,n x x x 的平均数11．（2021∙全国新Ⅰ卷∙高考真题）有一组样本数据1x ，2x ，…，n x ，由这组数据得到新样本数据1y ，2y ，…，n y ，其中i i y x c =+(1,2,,),i n c =⋅⋅⋅为非零常数，则（）A ．两组样本数据的样本平均数相同B ．两组样本数据的样本中位数相同C ．两组样本数据的样本标准差相同D ．两组样本数据的样本极差相同三、填空题12．（2020∙江苏∙高考真题）已知一组数据4,2,3,5,6a a -的平均数为4，则a 的值是 .13．（2019∙江苏∙高考真题）已知一组数据6，7，8，8，9，10，则该组数据的方差是 .考点04 变量间的相关关系1．（2024∙天津∙高考真题）下列图中，线性相关性系数最大的是（）A ．B ．C ．D ．2．（2023∙天津∙高考真题）鸢是鹰科的一种鸟，《诗经∙大雅∙旱麓》曰：“鸢飞戾天，鱼跃余渊”. 鸢尾花因花瓣形如鸢尾而得名，寓意鹏程万里、前途无量.通过随机抽样，收集了若干朵某品种鸢尾花的花萼长度和花瓣长度（单位：cm ），绘制散点图如图所示，计算得样本相关系数为0.8642r =，利用最小二乘法求得相应的经验回归方程为 0.75010.6105y x =+，根据以上信息，如下判断正确的为（）A ．花瓣长度和花萼长度不存在相关关系B ．花瓣长度和花萼长度负相关C ．花萼长度为7cm 的该品种鸢尾花的花瓣长度的平均值为5.8612cmD ．若从样本中抽取一部分，则这部分的相关系数一定是0.86423．（2020∙全国∙高考真题）某校一个课外学习小组为研究某作物种子的发芽率y 和温度x （单位：°C ）的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据(,)(1,2,,20)i i x y i = 得到下面的散点图：由此散点图，在10°C 至40°C 之间，下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是（）A ．y a bx =+B ．2y a bx =+C ．e x y a b =+D ．ln y a b x =+参考答案考点01 随机抽样1．（2023∙全国新Ⅱ卷∙高考真题）某学校为了解学生参加体育运动的情况，用比例分配的分层随机抽样方法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同的抽样结果共有（）．A ．4515400200C C ⋅种B ．2040400200C C ⋅种 C ．3030400200C C ⋅种 D ．4020400200C C ⋅种【答案】D【详细分析】利用分层抽样的原理和组合公式即可得到答案. 【答案详解】根据分层抽样的定义知初中部共抽取4006040600⨯=人，高中部共抽取2006020600⨯=，根据组合公式和分步计数原理则不同的抽样结果共有4020400200C C ⋅种.故选：D.考点02 图表类统计图综合1．（2022∙天津∙高考真题）为研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单位：kPa ）的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17]，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组，右图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为（）A ．8B ．12C ．16D ．18【答案】B 【详细分析】结合已知条件和频率分布直方图求出志愿者的总人数，进而求出第三组的总人数，从而可以求得结果. 【答案详解】志愿者的总人数为20(0.240.16)1+⨯＝50，所以第三组人数为50×0.36＝18，有疗效的人数为18－6＝12．故选：B.2．（2021∙天津∙高考真题）从某网络平台推荐的影视作品中抽取400部，统计其评分数据，将所得400个评分数据分为8组：[)66,70、[)70,74、L 、[]94,98，并整理得到如下的频率分布直方图，则评分在区间[)82,86内的影视作品数量是（）A ．20B ．40C ．64D ．80【答案】D 【详细分析】利用频率分布直方图可计算出评分在区间[)82,86内的影视作品数量.【答案详解】由频率分布直方图可知，评分在区间[)82,86内的影视作品数量为4000.05480⨯⨯=.故选：D.4．（2021∙全国甲卷∙高考真题）为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论中不正确的是（）A ．该地农户家庭年收入低于4.5万元的农户比率估计为6%B ．该地农户家庭年收入不低于10.5万元的农户比率估计为10%C ．估计该地农户家庭年收入的平均值不超过6.5万元D ．估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间【答案】C【详细分析】根据直方图的意义直接计算相应范围内的频率，即可判定ABD,以各组的中间值作为代表乘以相应的频率，然后求和即得到样本的平均数的估计值，也就是总体平均值的估计值，计算后即可判定C.【答案详解】因为频率直方图中的组距为1，所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.该地农户家庭年收入低于4.5万元的农户的比率估计值为0.020.040.066%+==,故A 正确；该地农户家庭年收入不低于10.5万元的农户比率估计值为0.040.0230.1010%+⨯==,故B 正确；该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为0.100.140.2020.6464%50%++⨯==>,故D 正确；该地农户家庭年收入的平均值的估计值为30.0240.0450.1060.1470.2080.2090.10100.10110.04120.02130.02140.027.68⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=(万元)，超过6.5万元，故C 错误.综上，给出结论中不正确的是C.故选：C.【名师点评】本题考查利用样本频率直方图估计总体频率和平均值，属基础题，样本的频率可作为总体的频率的估计值，样本的平均值的估计值是各组的中间值乘以其相应频率然后求和所得值，可以作为总体的平均值的估计值.注意各组的频率等于⨯频率组距组距. 5．（2020∙全国新Ⅱ卷∙高考真题）（多选）我国新冠肺炎疫情进入常态化，各地有序推进复工复产，下面是某地连续11天复工复产指数折线图，下列说法正确的是A ．这11天复工指数和复产指数均逐日增加;B ．这11天期间，复产指数增量大于复工指数的增量;C ．第3天至第11天复工复产指数均超过80%;D ．第9天至第11天复产指数增量大于复工指数的增量;【答案】CD【详细分析】注意到折线图中有递减部分，可判定A 错误；注意考查第1天和第11天的复工复产指数的差的大小，可判定B 错误；根据图象，结合复工复产指数的意义和增量的意义可以判定CD 正确.【答案详解】由图可知，第1天到第2天复工指数减少，第7天到第8天复工指数减少，第10天到第11复工指数减少，第8天到第9天复产指数减少，故A 错误；由图可知，第一天的复产指标与复工指标的差大于第11天的复产指标与复工指标的差，所以这11天期间，复产指数增量小于复工指数的增量，故B 错误;由图可知，第3天至第11天复工复产指数均超过80%，故C 正确;由图可知，第9天至第11天复产指数增量大于复工指数的增量，故D 正确;【名师点评】本题考查折线图表示的函数的认知与理解，考查理解能力，识图能力，推理能力，难点在于指数增量的理解与观测，属中档题.5．（2020∙天津∙高考真题）从一批零件中抽取80个，测量其直径（单位：mm ），将所得数据分为9组：[)[)[)[]5.31,5.33,5.33,5.35,,5.45,5.47,5.47,5.49 ，并整理得到如下频率分布直方图，则在被抽取的零件中，直径落在区间[5.43,5.47)内的个数为（）A ．10B ．18C ．20D ．36【答案】B 【详细分析】根据直方图确定直径落在区间[)5.43,5.47之间的零件频率，然后结合样本总数计算其个数即可. 【答案详解】根据直方图，直径落在区间[)5.43,5.47之间的零件频率为：()6.25 5.000.020.225+⨯=，则区间[)5.43,5.47内零件的个数为：800.22518⨯=.故选：B.【名师点评】本题主要考查频率分布直方图的计算与实际应用，属于中等题.考点03 样本的数字特征一、单选题1．（2024∙全国新Ⅱ卷∙高考真题）某农业研究部门在面积相等的100块稻田上种植一种新型水稻，得到各块稻田的亩产量（单位：kg ）并整理如下表亩产量[900，950） [950，1000） [1000，1050） [1050，1100） [1100，1150） [1150，1200）频数 6 12 18 30 24 10 根据表中数据，下列结论中正确的是（）A ．100块稻田亩产量的中位数小于1050kgB ．100块稻田中亩产量低于1100kg 的稻田所占比例超过80%C ．100块稻田亩产量的极差介于200kg 至300kg 之间D ．100块稻田亩产量的平均值介于900kg 至1000kg 之间【答案】C【详细分析】计算出前三段频数即可判断A ；计算出低于1100kg 的频数，再计算比例即可判断B ；根据极差计算方法即可判断C ；根据平均值计算公式即可判断D.【答案详解】对于 A, 根据频数分布表可知, 612183650++=<,所以亩产量的中位数不小于 1050kg , 故 A 错误；对于B ，亩产量不低于1100kg 的频数为341024=+，所以低于1100kg 的稻田占比为1003466%100-=，故B 错误；对于C ，稻田亩产量的极差最大为1200900300-=，最小为1150950200-=，故C 正确；对于D ，由频数分布表可得，平均值为1(692512975181025301075241125101175)1067100⨯⨯+⨯+⨯+⨯+⨯+⨯=，故D 错误. 故选；C.2．（2022∙全国乙卷∙高考真题）分别统计了甲、乙两位同学16周的各周课外体育运动时长（单位：h ），得如下茎叶图：则下列结论中错误的是（）A ．甲同学周课外体育运动时长的样本中位数为7.4B ．乙同学周课外体育运动时长的样本平均数大于8C ．甲同学周课外体育运动时长大于8的概率的估计值大于0.4D ．乙同学周课外体育运动时长大于8的概率的估计值大于0.6【答案】C【详细分析】结合茎叶图、中位数、平均数、古典概型等知识确定正确答案.【答案详解】对于A 选项，甲同学周课外体育运动时长的样本中位数为7.37.57.42+=，A 选项结论正确.对于B 选项，乙同学课外体育运动时长的样本平均数为：6.37.47.68.18.28.28.58.68.68.68.69.09.29.39.810.18.50625816+++++++++++++++=>， B 选项结论正确.对于C 选项，甲同学周课外体育运动时长大于8的概率的估计值60.3750.416=<， C 选项结论错误.对于D 选项，乙同学周课外体育运动时长大于8的概率的估计值130.81250.616=>， D 选项结论正确.故选：C3．（2022∙全国甲卷∙高考真题）某社区通过公益讲座以普及社区居民的垃圾分类知识．为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如下图：则（）A ．讲座前问卷答题的正确率的中位数小于70%B ．讲座后问卷答题的正确率的平均数大于85%C ．讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差D ．讲座后问卷答题的正确率的极差大于讲座前正确率的极差【答案】B【详细分析】由图表信息，结合中位数、平均数、标准差、极差的概念，逐项判断即可得解. 【答案详解】讲座前中位数为70%75%70%2+>,所以A 错；讲座后问卷答题的正确率只有一个是80%,4个85%,剩下全部大于等于90%,所以讲座后问卷答题的正确率的平均数大于85%,所以B 对；讲座前问卷答题的正确率更加分散,所以讲座前问卷答题的正确率的标准差大于讲座后正确率的标准差,所以C 错；讲座后问卷答题的正确率的极差为100%80%20%-=，讲座前问卷答题的正确率的极差为95%60%35%20%-=>,所以D 错.故选:B.4．（2020∙全国∙高考真题）在一组样本数据中，1，2，3，4出现的频率分别为1234,,,p p p p ，且411i i p ==∑，则下面四种情形中，对应样本的标准差最大的一组是（）A ．14230.1,0.4p p p p ====B ．14230.4,0.1p p p p ====C ．14230.2,0.3p p p p ====D ．14230.3,0.2p p p p ====【答案】B【详细分析】计算出四个选项中对应数据的平均数和方差，由此可得出标准差最大的一组.【答案详解】对于A 选项，该组数据的平均数为()()140.1230.4 2.5A x =+⨯++⨯=，方差为()()()()222221 2.50.12 2.50.43 2.50.44 2.50.10.65A s =-⨯+-⨯+-⨯+-⨯=；对于B 选项，该组数据的平均数为()()140.4230.1 2.5B x =+⨯++⨯=，方差为()()()()222221 2.50.42 2.50.13 2.50.14 2.50.4 1.85B s =-⨯+-⨯+-⨯+-⨯=；对于C 选项，该组数据的平均数为()()140.2230.3 2.5C x =+⨯++⨯=，方差为()()()()222221 2.50.22 2.50.33 2.50.34 2.50.2 1.05C s =-⨯+-⨯+-⨯+-⨯=；对于D 选项，该组数据的平均数为()()140.3230.2 2.5D x =+⨯++⨯=，方差为()()()()222221 2.50.32 2.50.23 2.50.24 2.50.3 1.45D s =-⨯+-⨯+-⨯+-⨯=. 因此，B 选项这一组的标准差最大.故选：B.【名师点评】本题考查标准差的大小比较，考查方差公式的应用，考查计算能力，属于基础题. 5．（2020∙全国∙高考真题）设一组样本数据x 1，x 2，…，xn 的方差为0.01，则数据10x 1，10x 2，…，10xn 的方差为（）A ．0.01B ．0.1C ．1D ．10【答案】C【详细分析】根据新数据与原数据关系确定方差关系，即得结果. 【答案详解】因为数据(1,2,,)i ax b i n +=L ，的方差是数据(1,2,,)i x i n =L ，的方差的2a 倍，所以所求数据方差为2100.01=1⨯故选：C【名师点评】本题考查方差，考查基本详细分析求解能力，属基础题.6．（2019∙全国∙高考真题）演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是A ．中位数B ．平均数C ．方差D ．极差【答案】A【详细分析】可不用动笔，直接得到答案，亦可采用特殊数据，特值法筛选答案．【答案详解】设9位评委评分按从小到大排列为123489x x x x x x ≤≤≤≤≤ ．则①原始中位数为5x ，去掉最低分1x ，最高分9x ，后剩余2348x x x x ≤≤≤ ，中位数仍为5x ，∴A 正确． ②原始平均数1234891()9x x x x x x x =+++++ ，后来平均数234817x x x x x '=+++ （）平均数受极端值影响较大，∴x 与x '不一定相同，B 不正确 ③()()()222219119S x x x x x x ⎡⎤=-+-++-⎣⎦ ()()()222223817s x x x x x x ⎡⎤'=-'+-'++-'⎢⎥⎣⎦ 由②易知，C 不正确． ④原极差91=x -x ，后来极差82=x -x 可能相等可能变小，D 不正确．【名师点评】本题旨在考查学生对中位数、平均数、方差、极差本质的理解.考点04 变量间的相关关系1．（2024∙天津∙高考真题）下列图中，线性相关性系数最大的是（）A ．B ．C ．D ．【答案】A【详细分析】由点的分布特征可直接判断【答案详解】观察4幅图可知，A 图散点分布比较集中，且大体接近某一条直线，线性回归模型拟合效果比较好，呈现明显的正相关，r 值相比于其他3图更接近1.故选：A2．（2023∙天津∙高考真题）鸢是鹰科的一种鸟，《诗经∙大雅∙旱麓》曰：“鸢飞戾天，鱼跃余渊”. 鸢尾花因花瓣形如鸢尾而得名，寓意鹏程万里、前途无量.通过随机抽样，收集了若干朵某品种鸢尾花的花萼长度和花瓣长度（单位：cm ），绘制散点图如图所示，计算得样本相关系数为0.8642r =，利用最小二乘法求得相应的经验回归方程为 0.75010.6105y x =+，根据以上信息，如下判断正确的为（）A ．花瓣长度和花萼长度不存在相关关系B ．花瓣长度和花萼长度负相关C ．花萼长度为7cm 的该品种鸢尾花的花瓣长度的平均值为5.8612cmD ．若从样本中抽取一部分，则这部分的相关系数一定是0.8642【答案】C【详细分析】根据散点图的特点及经验回归方程可判断ABC 选项，根据相关系数的定义可以判断D 选项.【答案详解】根据散点的集中程度可知，花瓣长度和花萼长度有相关性，A 选项错误散点的分布是从左下到右上，从而花瓣长度和花萼长度呈现正相关性，B 选项错误，把7x =代入 0.75010.6105y x =+可得 5.8612cm y =，C 选项正确；由于0.8642r =是全部数据的相关系数，取出来一部分数据，相关性可能变强，可能变弱，即取出的数据的相关系数不一定是0.8642，D 选项错误故选：C3．（2020∙全国∙高考真题）某校一个课外学习小组为研究某作物种子的发芽率y 和温度x （单位：°C ）的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据(,)(1,2,,20)i i x y i = 得到下面的散点图：由此散点图，在10°C 至40°C 之间，下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是（）A ．y a bx =+B ．2y a bx =+C ．e x y a b =+D ．ln y a b x =+ 【答案】D【详细分析】根据散点图的分布可选择合适的函数模型.【答案详解】由散点图分布可知，散点图分布在一个对数函数的图象附近，因此，最适合作为发芽率y 和温度x 的回归方程类型的是ln y a b x =+. 故选：D.【名师点评】本题考查函数模型的选择，主要观察散点图的分布，属于基础题.。

河南省驻马店市(新版)2024高考数学部编版测试(拓展卷)完整试卷

河南省驻马店市（新版）2024高考数学部编版测试(拓展卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题设抛物线的焦点为，准线与轴的交点为是上一点．若，则（）A．B．5C．D．第(2)题已知是三个不同的平面，是两条不同的直线，下列命题为真命题的是（）A．若，，则B．若，，则C．若，则D．若，则第(3)题已知函数的图象关于点中心对称，则（）A．3或B．2或C．或D．或第(4)题设，A分别是椭圆的左焦点和右顶点，点P为椭圆上异于A点的任意一点，则使得成立的点P的个数为（）A．1B．2C．3D．4第(5)题设向量, ,若表示向量的有向线段首尾相接能构成三角形,则向量等于( )A．B．C．D．第(6)题双曲线的焦点坐标为（）A．B．C．D．第(7)题已知平面向量满足：与的夹角为，若，则（）A．0B．1C．D．第(8)题若，，，则（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知函数，则下列说法中正确的有（）A ．函数的图象关于点对称B．函数图象的一条对称轴是C ．若，则函数的最小值为D．若，，则的最小值为第(2)题已知函数，令，则（）A．当，恒成立B．函数在区间上单调递增C．a，b，c中最大的是c D．a，b，c中最小的是a第(3)题如图，点是直线上的动点，点在直线外，点在直线上，则（）A．有最小值B．有最大值C．D．直线上有且只有一点(不同于点)，使得三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知三棱锥的体积为，其外接球的体积为，若，，则线段的长度的最小值为___________.第(2)题函数在点处的切线方程是______．第(3)题已知O为坐标原点，椭圆的左焦点为F，A为C上一点，AF与x轴垂直．若的面积为，则C的离心率为__________．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知抛物线过点，O为坐标原点.(1)求抛物线的方程；(2)直线l经过抛物线的焦点，且与抛物线相交于A，B两点，若弦AB的长等于6，求的面积；(3)抛物线上是否存在异于O，M的点N，使得经过O，M，N三点的圆C和抛物线在点N处有相同的切线，若存在，求出点N的坐标，若不存在，请说明理由.第(2)题将数列中项数为平方数的项依次选出构成数列，此时数列中剩下的项构成数列；再将数列中项数为平方数的项依次选出构成数列，剩下的项构成数列；…．如此操作下去，将数列中项数为平方数的项依次选出构成数列，剩下的项构成数列．(1)分别写出数列的前2项；(2)记数列的第项为．求证：当时，；(3)若，求的值．第(3)题已知函数.（1）若是函数的极值点，求的单调区间；（2）当时，证明：第(4)题华为手机的“麒麟970”芯片在华为处理器排行榜中最高主频2.4GHz，同时它的线程结构也做了很大的改善，整个性能及效率至少提升了50%，科研人员曾就是否需采用西门子制程这一工艺标准进行了反复比较，在一次实验中，工作人员对生产出的50片芯片进行研究，结果发现使用了该工艺的30片芯片有28片线程结构有很大的改善，没有使用该工艺的20片芯片中有12片线程结构有很大的改善.（1）用列联表判断：这次实验是否有99.5%的把握认为“麒麟970”芯片的线程结构有很大的改善与使用西门子制程这一工艺标准有关？（2）在“麒麟970”芯片的线程结构有很大的改善后，接下来的生产制作还需对芯片的晶圆依次进行金属溅镀，涂布光阻，蚀刻技术，光阻去除这四个环节的精密操作，进而得到多晶的晶圆，生产出来的多晶的晶圆经过严格的质检，确定合格后才能进入下一个流程.如果生产出来的多晶的晶圆在质检中不合格，那么必须依次对前四个环节进行技术检测并对所有的出错环节进行修复才能成为合格品.在实验的初期，由于技术的不成熟，生产制作的多晶的晶圆很难达到理想状态，研究人员根据以往的数据与经验得知在实验生产多晶的晶圆的过程中，前三个环节每个环节生产正常的概率为，每个环节出错需要修复的费用均为200元，第四环节生产正常的概率为，此环节出错需要修复的费用为100元，问：一次试验生产出来的多晶的晶圆要成为合格品大约还需要消耗多少元费用？（假设质检与检测过程不产生费用）参考公式：，.参考数据：0.150.100.050.0250.010.0050.0012.072 2.0763.841 5.024 6.6357.87910.828第(5)题已知圆心为D的动圆经过定点，且内切于圆．(1)求动点D的轨迹C的方程；(2)直线与C相交于两点，过C上的点P作x轴的平行线交线段于点Q，直线的斜率为k（O为坐标原点），的面积为，的面积为，若，判断：是否为定值？并说明理由．。

河南省各地市高考数学最新联考试题分类大汇编(14)统计.doc

河南省各地市高考数学最新联考试题分类大汇编
第14部分:统计
一、选择题：
3．(河南省焦作、开封两市高三二模联考理科)某单位有业务人员1管理人员24人，后勤人员16人. 现用分层抽样的方法，从该单位职工中抽取一个容量为n的样本，已知从管理人员中抽取3人，则n为（ A ）
A. B. 30 C. 40 D. 50
3．（河南省郑州市高三第二次质量检测文科）某市有高中毕业生30 000人，其中文科学生8 000人．为调查学生的复习备考情况，采用分层抽样的方法抽取一个容量为150的样本，则样本中文科学生的数量应为（ A ）
A 40 B．30 C． D．10
二、填空题：
15．（河南省新乡平顶山许昌高三下学期第二次调研理随机抽查某中学高三年级100名学生的视力情况，得其频率分布直方图如下图所示。

已知前4组的频数成等比数列，后6组的频数成等差数列，则视力在4.5到5.0之间的学生人数为 87 人。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

河南省各地市高考数学最新联考试题分类汇编（15）复数与推理证
明
一、选择题:
11．(河南省开封市高三第一次模拟考试理)茌发生某公共卫生事件期间，有专业机构认为
该事件在一段时间内没有发生大规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”．根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是（） A ．甲地：总体均值为3，中位数为4 B ．乙地：总体均值为1，总体方差大予
C ．丙地：中位数为2，众数为3
D ．丁地：总体均值为2，总体方差为3 【答案】D
8、(河南省焦作市高三第一次模拟文)在样本频率分布直方图中，一共有n 个小矩形，若中间一个小矩形的面积等于其余n －1个小矩形面积之和的
1
4
，且样本容量为160，则中间一组的频数是
A 、32
B 、20
C 、40
D 、25 【答案】A
3．(河南省信阳高中 4月高三模拟一理）以下有关线性回归分析的说法不正确．．．
的是 A ．通过最小二乘法得到的线性回归直线经过样本的中心(,)x y B ．用最小二乘法求回归直线方程，是寻求使
2
1
()
n
i
i
i y bx a =--∑最小的a ,b 的值
C ．相关系数r 越小，表明两个变量相关性越弱
D ．2
2
1
2
1
()
1()
n
i
i
i n
i
i y y R y y ==-=-
-∑∑越接近1，表明回归的效果越好
【答案】C
5. (河南省三市平顶山、许昌、新乡高三第三次调研理)图1是某县参加高考的学生身高的统计图，从左到右的条形图表示学生人数一次记为
12310,,,A A A A (
2
A 表示身高（单位：
cm ）在[150,155)的人数)。

图2是统计图1中身高在一定范围内学生人数的一个算法流程图，先要统计身高在160180cm （含160cm,不含180cm ）的学生人数，那么在流程图的判断框内应填写的条件是
A. 6i <
B. 7i <
C. 8i <
D. 9i <
【答案】C 二、填空题:
13．(河南省六市高中毕业班第一次联考文)已知x 、y 的取值如下表所示：若y 与x 线性
相关，且ˆy
＝0．95x ＋a ，则a ＝_______. x 0 1 3 4 y
2．2
4．3
4．8
6．7
【答案】
三、解答题:
18. (河南省郑州市高三第二次质量预测理) (本小题满分12分）
每年的三月十二日，是中国的植树节.林管部门在植树前，为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两批树苗中各抽测了 10株树苗的高度，规定高于128厘米的为“良种树苗”,测得高度如下(单位:厘米）
甲：137，121,131，120,129，119,132，123,125,133 乙：110,130,147,127,146,114，126,110,144，146 (I)根据抽测结果，完成答题卷中的茎叶图，并根据你填写的茎叶图，对甲、乙两批树苗的高度作比较，写出对两种树苗高度的统计结论；
(II)设抽测的10株甲种树苗髙度平均值为
将这10株树苗
的高度依次输人按程序框图进行运算，（如图）问输出的S 大小为多少？并说明S 的统计学意义；
(III)若小王在甲批树苗中随机领取了 5株进行种植，用样本
的频率分布估计总体分布，求小王领取到的“良种树苗”株数X的分布列.
18.(河南省豫东、豫北十所名校高三阶段性测试四) (本小题满分12分）
某园艺师用两种不同的方法培育了一批珍贵树苗，在树苗3个月大的时候，随机抽取甲、乙两种方式培育的树苗各20株，测量其髙度，得到的茎叶图如图（单位:cm):
(I )依茎叶图判断用哪种方法培育的树苗的平均高度大？
(II)现从用甲种方式培育的高度不低于80 cm的树苗中随机抽取两株，求高度为 86 cm 的树苗至少有1株被抽中的概率；
(III)如果规定高度不低于85 cm的为生长优秀，请填写下面的2 x2列联表，并判断“能否在犯错误的概率不超过的前提下认为树苗高度与培育方式有关?”
下面临界值表仅供参考：
(参考公式:
（18）解：（Ⅰ）用甲种方式培育的树苗的高度集中于60～90 cm之间，而用乙种方式培育的树苗的高度集中于80～100 cm之间，所以用乙种方式培养的树苗的平均高度大.……（3分）
（Ⅱ）记高度为86 cm的树苗为,A B，其他不低于80 cm的树苗为,,,,
C D E F“从用甲种方式培育的高度不低于80 cm的树苗中随机抽取两株”，基本事件有：
(,),(,),(,),(,),(,),(,),(,),(,),(,),
A B A C A D A E A F B C B D B E B F
(,),(,),(,),(,),(,),(,),
C D C E C F D E D F E F共15个.…………………………………（5分）“高度为86 cm的树苗至少有一株被抽中”所组成的基本事件有：
(,),(,),(,),(,),(,),(,),(,),(,),(,),
A B A C A D A E A F B C B D B E B F共9个，……………（7分）
故所求概率
93
.
155
P==……………………………………………………………………（8
分）
（Ⅲ）
…………………………（9
分）
2
K 的观测值k 2
40(3101017) 5.584 5.024********
⨯⨯-⨯=
≈⨯⨯⨯＞，……………………………（11分）
因此在犯错误的概率不超过的前提下可以认为树苗的高度与培育方式有关.…（12分） 18．(河南省信阳高中 4月高三模拟一理）
（本小题满分12分）
某学生社团在对本校学生学习方法开展问卷调查的过程中发现，在回收上来的1000份有效问卷中，同学们背英语单词的时间安排共有两种：白天背和晚上临睡前背。

为研究背单词时间安排对记忆效果的影响，该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样，并完成一项实验，实验方法是，使两组学生记忆40个无意义音节（如XIQ 、GEH ），均要求在刚能全部记清时就停止识记，并在8小时后进行记忆测验。

不同的是，甲组同学识记结束后一直不睡觉，8小时后测验；乙组同学识记停止后立刻睡觉，8小时后叫醒测验。

两组同学识记停止8小时后的准确回忆（保持）情况如图（区间含左端点而不含右端点）
（1）估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数；
（2）从乙组准确回忆因结束在[12,24)范围内的学生中随机选3人，记能准确回忆20个以上（含20）的人数为随机变量X ，求X 分布列及数学期望；（3）从本次实验的结果来看，上述两种时间安排方法中哪种方法背英语单词记忆效果更好? 计算并说明理由。

甲方式
乙方式
合计
优秀 3 10 13 不优秀 17 10 27 合计
20
20
40。