组合图形的面积1
小学五年级奥数第18讲 组合图形的面积(含答案分析)

第18讲组合图形面积(一)一、知识要点组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4,采用割、补、分解、代换等方法,可将复杂问题变得简单。
二、精讲精练【例题1】一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?练习1:1.求四边形ABCD的面积。
(单位:厘米)2.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3.有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
【例题2】正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
练习2:1.(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积。
2.正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3.求下图(上右图)长方形ABCD的面积(单位:厘米)。
【例题3】四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?练习3:1.图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
2.下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)3.下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?【例题4】下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?练习4:1.如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积。
组合图形的面积公式

组合图形的面积公式许多天文学家和数学家经常发现,天文和数学形状的总体面积可以通过不同的图形组合而成。
经常的形状可以是三角形、正方形、圆形、多边形和椭圆形等。
为了计算组合图形的总体面积,我们需要知道每个组件面积的公式,以及它们如何组合在一起。
下面,我将介绍组合图形的常用面积公式。
1、三角形面积公式三角形的面积可以通过三角形的底边长与其高的乘积来确定。
如果三角形的底边长是a,其高为h,则可以通过以下公式确定三角形的面积:S = 1/2 a h2、正方形面积公式正方形的面积可以通过其边长乘积来确定。
如果正方形的边长是a,则可以通过以下公式确定正方形的面积:S = a a3、圆形面积公式圆形的面积可以通过圆形的半径乘以π来确定。
如果圆形的半径是r,则可以通过以下公式确定圆形的面积:S = r r4、多边形面积公式多边形的面积可以通过多边形的顶点与其中心的距离乘积来确定。
如果多边形的顶点是A,它的中心距离为d,则可以通过以下公式确定多边形的面积:S=1/2 A d5、椭圆形面积公式椭圆形的面积可以通过椭圆形的长轴与短轴的乘积来确定。
如果椭圆形的长轴是a,它的短轴是b,则可以通过以下公式确定椭圆形的面积:S = a b以上就是组合图形的常用面积公式。
当在计算更复杂的组合形状时,可以使用多边形分解法来计算总面积。
这种方法可以将复杂的多边形分解为若干较小的多边形,然后在每个小多边形上应用前面提到的面积公式,最后将每个小多边形的面积相加,从而获得总面积。
总之,组合图形的面积计算可以通过不同图形的面积公式进行计算,也可以通过多边形分解方法来计算总面积。
不同结构的图形可以有不同的面积计算方法,但基本思路都是将复杂的形状分成若干个简单的形状,以最简单的形状的面积公式为基础,求出复杂形状的面积值。
通过学习和研究以上计算面积的方法,可以帮助我们更好地解决天文学和数学中的组合图形的面积计算问题。
五年级数学组合图形的面积1

2cm
4cm
4cm 4cm 4cm
丁丁 丁丁和当当谁能 计算出组合图形 的面积?
当当
练习2:
有一面墙,粉刷这面墙每平方米需用 0.15千克涂料,一共需用多少千克涂料?
-----1.6m--2 2 =40+8=48( )
S长=ab S正= a2 S平=ah S△=ah÷2
S梯=(a+b)h÷2
像这样的图形我们把 它 们叫做组合图形。
(北师大版)五年级数学(上册)
组合图形面积
小华家新买了住房,计划在客厅铺地 板(客厅平面图如下)。爸爸买了42 平方米的地板,请你估计多了还是少 了。
至少需要多少平方米地板?
练一练1.
m
48×0.15=7.2(千克)
4m
答:一共需用7.2千克涂 料。
10m
练一练3. 如图,一张硬纸板剪下4个边长是4厘 米的小正方形后,可以做成一个没有盖子 的盒子。这张硬纸板还剩下多大的面积?
4cm
20cm
长方形-4个正方形
26cm
26×20-4×4×4
人教版五年级上册数学组合图形的面积1

生活中的组合图形
由两个完全 一样的梯形 组合成的
由一个长方形 和两个完全一 样的三角形组 合成的
一个长方形去 掉一个三角形 而得到的图形。
什么样的图形是组 合图形?
由两个或两个以上图形组合而 成的图形,叫组合图形。
生活中哪些地方有组合图形?
我家窗户上有组 合图形。
我的飞机模型 上也有。
6cm
=33(cm2)
7cm
练一练 分割成一个长方形和一个正方形
4cm
4×6+3×3
3cm
6cm
3cm
=24+9 =33(cm2)
7cm
练一练
4cm
分割成两个梯形
(3+7)×3÷2+(3+6)×4÷2
3cm 7cm
3cm
6cm
3cm
练一练 分割成一个长方形和一个正方形
4cm
3cm
3cm
7×6-3×3 =42-9 =33(cm2)
这就是我们刚才看到的 一间房子的侧面墙,它的 面积有多大呢? 请同学们小组合作,利 用手中的答题卡,先讨论 方法,并画一画,再说一 说这个图形的面积该怎样 求?
方法一 分割法
方法二
方法三 添补法
方法一:三角形的面积+正方形的面积 5×2÷2+5×5 =5+25 =30(m2)
方法二:直角梯形的面积×2 5+2=7(m) 5÷2=2.5(m) (5+7)×2.5÷2×2 =12×2.5÷2×2 =30 (m2)
40m 30m 30m 70m
15m
2、学校校园里有一块长方形的 地,想种上红花、黄花和绿草。 一种设计方案如图。你能分别算 出红花、黄花、绿草的种植面积 吗?
第2讲 组合图形的面积(一)(5年级)
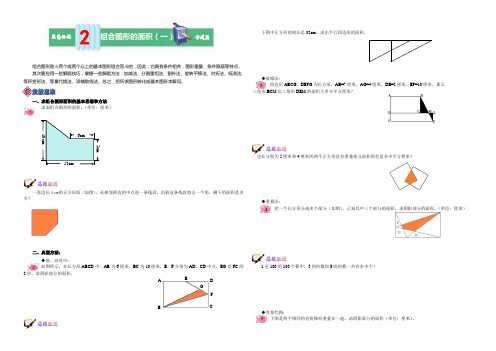
5820组合图形是由两个或两个以上的基本图形组合而成的,因此,它具有条件相共,图形重叠、条件隐蔽等特点。
其次要应用一些解题技巧,掌握一些解题方法:加减法、分割重组法、割补法、旋转平移法、对折法、抵消法、等积变形法、等量代换法、添辅助线法。
总之,把所求图形转化成基本图形本解问。
一、求组合图形面积的基本思想和方法 求面组合图形的面积。
(单位:厘米)一张边长4㎝的正方形纸(如图),从相邻两边的中点连一条线段,沿着这条线段剪去一个角,剩下的面积是多少?二、典型方法:◆底、高对应:如图所示,在长方形ABCD 中,AB 为6厘米,BC 为10厘米,E 、F 分别为AD 、CD 中点,EG 是FC 的2倍。
求阴影部分的面积。
下图中正方形的周长是32cm 。
求出平行四边形的面积。
◆放缩法:四边形ABCG 、DEFG 为长方形,AB=7厘米,AG=4厘米,DE=2厘米,EF=10厘米,那么 三角形BCM 比三角形DEM 的面积大多少平方厘米?边长分别为5厘米和4厘米的两个正方形没有重叠部分面积的差是多少平方厘米?◆重叠法:把一个长方形分成多个部分(如图),已知其中三个部分的面积,求阴影部分的面积。
(单位:厘米)1至100的100个数中,3的倍数和5的倍数一共有多少个?◆等量代换: 式 下图是两个相同的直角梯形重叠在一起,求阴影部分的面积(单位:厘米)。
蓝色镭霆专题篇组合图形的面积(一)2AB DC F E G 10cm5cm12cm6cm 4 54.5分米10.5分米ABD E F CAB如图,正方形ABCD的边长为4厘米,长方形DEFG 的长DG 为5厘米。
长方形的宽是多少厘米?◆平衡法(方程): 如图三角形EFD 的面积比三角形ABF 的面积大6平方厘米,求ED 的长度是多少厘米?如图,梯形ABCD 的面积为45平方厘米,高6厘米,三角形AED 的面积为5厘米,求阴影部分的面积。
1、如图,阴影部分的面积是42平方分米,梯形的面积是多少平方分米?2、如图已知正方形ABCD 的周长是36厘米,DE 是的CE 的2倍,阴影部分的面积是多少平方厘米?3、如图,在直角梯形ABCD 中,AB=15厘米,AD=12厘米,阴影部分的面积为15平方厘米,梯形ABCD 的面积为多少平方厘米? 5、下图中大平行四边形的面积是36平方厘米。
2023五年级《组合图形面积》教学设计_1

2023五年级《组合图形面积》教学设计2023五年级《组合图形面积》教学设计1教材分析《组合图形的面积》是第五单元的第一课。
学生在三年级已学习了长方形和正方形的面积计算,在教材第二单元又学习了平行四边形、三角形和梯形的面积计算,本课组合图形面积的计算是这些知识的延展,也是实际生活中需要解决的问题。
在已有知识基础上学习组合图形,一方面可以巩固基本图形的面积计算,另一方面还能将所学知识加以综合运用,提高学生解决实际问题的综合能力。
学情分析作为五年级的学生,通过之前的学习对于平面基本图形的感知和认识已有了一定的基础,也掌握了一些计算图形面积和解决图形问题的方法。
但本班学生分析思考能力较差,基础较薄弱,所以应进一步提高知识的综合运用能力,加强团体合作精神,善于去交流思考,探索解决问题的策略。
教学目标教学目的:1、在自主探索活动中,理解计算组合图形面积的多种方法。
2、能根据各种组合图形的条件,有效地选择计算方法并进行正确的解答。
3、能运用所学的知识,解决生活中组合图形的实际问题。
情感、态度和价值观:1、通过联系生活实际,使学生感受到计算组合图形面积的必要性。
2、学生通过参与探索活动,思维得到拓展,能力得到了提升,同时也掌握了多种解题策略。
3、通过小组探索研究,使学生认识到与人合作的重要性,从而加强合作意识。
过程和方法:1、在解决组合图形面积时,通过认真观察,独立思考、自主探索寻找解决问题的策略。
2、通过小组讨论交流,理解解决问题的多种策略,从而经过比较选择最好的解题方法。
教学重点和难点重点:能正确计算组合图形的面积。
难点:能根据各种组合图形的条件,正确选择计算方法并解答。
2023五年级《组合图形面积》教学设计2【教学内容】北师大版五年级上册数学教科书第75页。
【设计理念】主要设计理念是:一是以学生为课堂学习的主体,关注学生已有的学习基础和学习经验,选择适合学生的学习素材、设计适合学生的教学活动,让学生自主的投入学习,教师是学生课堂学习的引导者、合作者。
五年级 图形题面积计算(必练题题库)
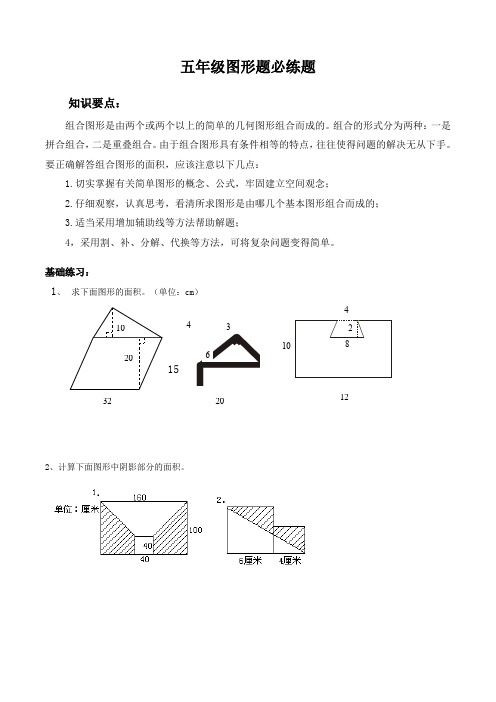
五年级图形题必练题知识要点:组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4,采用割、补、分解、代换等方法,可将复杂问题变得简单。
基础练习:1、 求下面图形的面积。
(单位:cm )152、计算下面图形中阴影部分的面积。
2010643482 1032 201230dm12dm 5m25dm 5m3、求下列阴影部分的面积。
① ②已知S 平=48dm 2,求S 阴。
③已知:阴影部分的面积为24④求S 阴。
平方厘米,求梯形的面积。
4、求下面各图形的面积。
(单位:分米)3m13cm 16cm8dm3dm12cm 7cm4dm8dm5、“实践操作”显身手:10分6、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
7、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)8、如图,这个长方形的长是9厘米,宽是8厘米,A 和B 是宽的中点,求长方形内阴影部分的面积。
9、在右图中,三角形EDF 的面积比三角形ABE 的面积大6平方厘米,已知长方形ABDC 的长和宽分别为6厘米、4厘米,DF 的长是多少厘米?16cm12cm14cm 24m10m8m1、求下面图形中阴影部分的面积。
2、求下面图形的面积。
10、右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
11、如图,三角形ABC的面积是24平方厘米,且DC=2AD,E、F分别是AF、BC的中点,那么阴影部分的面积是多少?12、如图,三角形ABC的面积是90平方厘米,EF平行于BC,AB=3AE,那么三角形甲、乙、丙的面积各是多少平方厘米?13、如图长方形,长18厘米,宽12厘米,AE、AF两条线段把长方形面积三等分,求三角形AEF的面积。
《公顷、平方千米》组合图形的面积PPT课件(1)

天安门广场的面积约是400000m2,相当于40公顷。
1000000
100
平方厘米 平方分米 平方米
公 顷 平方千米
×100 ×100 ×10000 ×100
1.到学校的操场上实际走一走,与同伴交流1公顷 有多大。
2.右图是某博物馆的一块介绍牌。读一读,你觉得
牌子介绍的内容对吗?与同伴说一说你的理由。
老虎生活在亚洲,号称“兽中之 王”,东北虎是虎中体型最大的 。世界上的几种老虎都已经成为 濒危珍稀物种。1983年初在东北 地区进行的航行调查表明,在 7000平方米的山林中仅发现两只 老虎,因此东北虎被列为一级保 护动物。
3.在横线上填上合适的面积单位(m2、公顷、km2)。
»
一、我们因梦想而伟大,所有的成功者都是大梦想家:在冬夜的火堆旁,在阴天的雨雾中,梦想着未来。有些人让梦想悄然绝灭,有些人则细心培育维护,直到它安然度过困境,迎来光明和希望,而光明和希望总是降临在那些真心相信梦想一定会成真的人身上。——威尔逊
•
二、梦想无论怎样模糊,总潜伏在我们心底,使我们的心境永远得不到宁静,直到这些梦想成为事实才止;像种子在地下一样,一定要萌芽滋长,伸出地面来,寻找阳光。——林语堂
•
二十九、梦想家命长,实干家寿短。——约·奥赖利
•
三十、青年时准备好材料,想造一座通向月亮的桥,或者在地上造二所宫殿或庙宇。活到中年,终于决定搭一个棚。——佚名
•
三十一、在这个并非尽善尽美的世界上,勤奋会得到报偿,而游手好闲则要受到惩罚。——毛姆
•
三十二、在科学上没有平坦的大道,只有不畏劳苦,沿着陡峭山路攀登的人,才有希望达到光辉的顶点。——马克思
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4x6=24(cm 2)
6cm 4cm
4cm
(4+6)x4÷2=20(cm 2)
组合图形是由两个或两个以上简单的基本图形组合而成的。
老师家新买了住房,计划在客厅铺地板(客厅平面图如下)。请你 估计老师家至少要买多大面积的地板,再实际算一算,并与同学进行交流。
老师家新买了住房,计划在客厅铺地板(客厅平面图如下)。请你 估计老师家至少要买多大面积的地板,再实际算一算,并与同学进行交流。
[(6―3)+6]x4÷2+[(7―4)+7]x3÷2 =18+15 =33(m2)
老师家新买了住房,计划在客厅铺地板(客厅平面图如下)。请你 估计老师家至少要买多大面积的地板,再实际算一算,并与同学进行交流。
7x6―(6―3)x(7―4) =42―9 =33(m2)
老师家新买了住房,计划在客厅铺地板(客厅平面图如下)。请你 估计老师家至少要买多大面积的地板,再实际算一算,并与同学进行交流。
16x8-6x2=116(m2 )
1.6m 4m
右图表示的是老师家 房子侧面墙的形状, 粉刷这面墙每平方米 需用0.15千克涂料, 一共要用多少千克涂 料?
10×4+10×1.6÷2 =40+8
10m
=48(㎡)
48×0.15=7.2(㎏)
1.6m 4m
右图表示的是老师家 房子侧面墙的形状, 粉刷这面墙每平方米 需用0.15千克涂料, 一共要用多少千克涂 料?
(4+7)x(6―3) =11x3 =32、分割的图形要最少。 3、分割的图形要能计算。
思考:你会选择哪种方法计算这两个图形的面积?
10m
2m
6m
10m 8m
6m
14m 分割法
16m 添补法
+
6x10+(10+14)x(10-6 ) ÷2=108(㎡ )
努 力 吧 !
一张硬纸板剪下4个边长是4厘米的小正方 形后,可以做成一个没有盖子的盒子。这 张硬纸板还剩下多大的面积?
26cm
20cm
8cm 4cm
如图,有两个边长是8cm的正方形放在桌面 上,求被盖住的桌面的面积。
4cm 8cm
求下列图形中阴影部分的面积。
求下列图形中阴影部分的面积。
谢谢
4x6+3x(7―4) =24+9 =33(m2)
老师家新买了住房,计划在客厅铺地板(客厅平面图如下)。请你 估计老师家至少要买多大面积的地板,再实际算一算,并与同学进行交流。
4x(6―3)+7x3 =12+21 =33(m2)
老师家新买了住房,计划在客厅铺地板(客厅平面图如下)。请你 估计老师家至少要买多大面积的地板,再实际算一算,并与同学进行交流。
组织引导者 张萃
S=a×b
S=a×a
S=a×h÷2
S=a×h
S=(a+b) ×h÷2
4cm
4cm
8cm
5cm
8cm
4cm 6cm
6cm 4cm
4cm
现在你能计算这些基本 本图形的面积吗?
4cm
8cm
4x8=32(cm 2)
5cm
5x5=25(cm2)
4cm 8cm
8x4÷2=16(cm2)
4cm 6cm
10m
分割成两个完全一样的梯形。
(4+5.6)×5÷2×2=48(㎡)
48×0.15=7.2(㎏)
老师家要油漆6扇门的正面。(单位:米) ⑴需要油漆的面积一共是多少? ⑵如果每平方米需要花费5元,那么老师共 要花费多少元?
⑴2×0.8-0.3×0.4
=1.6-0.12 =1.48(㎡) 1.48×6=8.88(㎡) ⑵8.88×5=44.4(元)
