高一三角同步练习6(化简与证明)
必修4--三角函数的化简、求值与证明综合练习

必修4—三角函数的化简、求值与证明练习A 组1、已知θ是第三象限角,且4459sin cos θθ+=,那么2sin θ等于---------------( ) A、3 B、3- C 、23 D 、23-2、函数222y sin x x =-+的最小正周期 -------------------------------( )A 、2πB 、πC 、3πD 、4π3、tan 70cos10201)-等于 -------------------------------------------------( )A 、1B 、2C 、-1D 、-24、已知46sin (4)4m m mαα-=≠-,则实数m 的取值范围是______。
5、设10,sin cos 2απαα<<+=,则cos2α=_____。
6、化简:42212cos 2cos 2.2tan()sin ()44x x x x ππ-+-+ 7、设3177cos(),45124x x πππ+=<<,求2sin 22sin 1tan x x x +-的值。
8、求证:sin(2)sin 2cos().sin sin αββαβαα+-+=9、已知11sin()cos [sin(2)cos ],022αβααβββπ+-+-=<<,求β的值。
10、 已知tan 2α=2,求(I )tan()4πα+的值; (II )6sin cos 3sin 2cos αααα+-的值.11、已知函数2()2sin sin 2,[0,2].f x x x x =+∈π求使()f x 为正值的x 的集合.12、已知函数f (x )=-3sin 2x +sin x cos x .(Ⅰ) 求f (256π)的值; (Ⅱ) 设α∈(0,π),f (2α)=41,求sin α的值.B 组1、已知1sin()43πα-=,则cos()4πα+的值等于-----------------------------------( ) A、3 B、3- C 、13 D 、13-2、已知tan α、tan β是方程240x ++=的两根,且(,)22ππαβ∈-、,则αβ+等于 ------------------------------------------------------------------------------------------------( )A 、3π B 、23π- C 、3π或23π- D 、3π-或23π3、化简23cos (1sin )[2tan()]422cos ()42x xx x ππ+---为 --------------------------------( )A 、sin xB 、cos xC 、tan xD 、αtan 14、22sin 2cos 1cos 2cos 2⋅=+αααα-------------------------------------------------------------------( )(A) tan α (B) tan 2α (C) 1 (D)125、函数⎪⎩⎪⎨⎧≥<<-π=-0,01),sin()(12x e x x x f x ,若2)()1(=+a f f ,则a 的所有可能值为( )(A )1 (B )22,1- (C )22- (D )22,1 6、设a 为第四象限的角,若 513sin 3sin =a a ,则tan 2a =______________. 7、已知tan2α=2,则tanα的值为 ,tan ()4πα+的值为8、已知tan()34πθ+=,则2sin 22cos θθ-的值为_______。
高一数学,三角函数同步练习题,同角三角函数化简与证明

三角函数同步练习6:同角关系化简与证明一、选择题1、已知cos α= - 1213,α∈(π,2π),则tan α的值是 ( ) A .513 B .512 C .125 D .± 5122、化简 160tan 112+的结果为 ( )A .-cos160°B .cos160°C .±cos160°D .-sec160°3、若是α第二象限角,则1sin 1tan 2-αα化简的结果是 ( ) A .1 B .-1 C .tan 2α D .-tan 2α4、若0cot tan cos cos sin sin 22=++θθθθθθ,则θ不可能是 ( )A .第一、第二、第三象限角B .第一、第二、第四象限角C .第一、第三、第四象限角D .第二、第三、第四象限角5、如果角θ满足1cos sin =+θθ,那么θθcot tan +的值是 ( )A .1-B .0C .1D .不存在6、若θ为二象限角,且2cos 2sin 212sin 2cosθθθθ-=-,那么2θ是A .第一象限角B .第二象限角C .第三象限角D .第四象限角7、若2tan =x , 则()()x x x x sin cos cos 3sin 1--的值为:A .3-B .5-C .3D .58、函数()=x f 1cos 1tan 2tan 1cos 122-++x x xx 值域中元素的个数是( ) A .1个 B .2个 C .3个 D .4个二、填空题1、化简sin 2α+sin 2β-sin 2αsin 2β+cos 2αcos 2β=.2、化简40sin 140sin 40cos 40sin 212---= .3、若ααααsin 1sin 1sin 1sin 1+---+ = -2 tan α,则角α的取值范围是 .三、解答题1、化简:tan α(cos α-sin α)+ααααcos 1)tan (sin sin ++.2、求证:1tan 1tan cos sin cos sin 2122-+=-+αααααα.3、求证:ααααααααcot tan cos sin 2cot cos tan sin 22+=++.4、已知cos B = cos θsin A , cos C = sin θsin A ,求证:sin 2A +sin 2B +sin 2C = 2.参考答案一、选择题BABB DCDD二、填空题1、1;2、αtan 1-;3、()Z k k k ∈+<<+,22322ππαππ 三、解答题1、αsin2、左边αααααα2222cos sin cos sin 2cos sin -++=()αααα222cos sin cos sin -+= =-+=-+=1tan 1tan cos sin cos sin αααααα右边. 3、 ∵()()()ααααααααααcot cos 1tan sin 1cot cos tan sin cot tan 2222-+-=+-+ ααααααααααcos sin 2cos sin sin cos cot sin tan cos 22=+=+= ∴ααααααααcot tan cos sin 2cot cos tan sin 22+=++.4、∵A B 222sin cos cos θ=,A C 222sin sin cos θ=,∴()A C B 22222sin sin coscos cos θθ+=+, 即:A C B 222sin sin 1sin 1=-+-,∴2sin sin sin 222=++C B A .。
(完整版)三角函数化简求值证明技巧
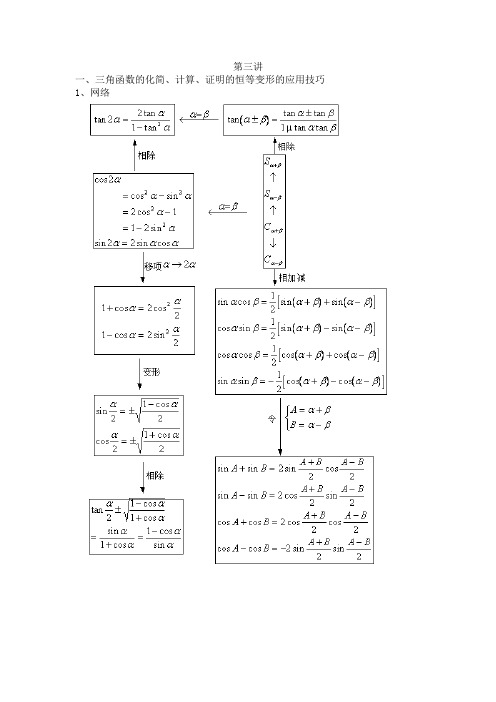
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
三角函数化简和证明()

三角函数的化简、求值与证明(3)主化锐:当已知角是90 到360内的角时,可利用180,270,360ααα--- 的诱导公式把这个角的三角函数值化为0 到90 内的角.二. 两角和与差的三角函数公式1. 两角和与差的正弦公式:()sin αβ±=______________.变形式:()()sin sin αβαβ++-=_______()();sin sin αβαβ+--=_______;2.两角和与差的余弦公式:()cos αβ±=__________________变形式:()()cos cos αβαβ++-=_____________;()()cos cos αβαβ+--=__________;3.两角和与差的正切公式:()tan αβ±=___________())2k k Z παβαβπ+≠+∈(、、.变形式:tan tan αβ±=_________________.【例1】计算:2(sincos )tan()643πππ++-=【例2】已知tan α=sin()cos()()sin()sin()n n n n n αααα+π-π∈+π+-πZ 的值.【例3】函数()cos()sin(),22xx f x x =-+π-∈R . (1)求()f x 的最小正周期有最大值; (2)求)(x f 在[0,)π上的减区间.【例4】若[0,2α∈π]sin co s αα=+,则α的取值范围是( ) A.(0,)2π B.(,)2ππ C.(,)23ππ D.(,2)23ππ【例5】已知关于x 的方程221)0x x m -++=的两根为s i nc o s θθ、,其中(0,2)θπ∈.(1)求m 的值;(2)求sin cos 1cot 1tan θθθθ+--的值.【例6】已知02x π-<<,1sin cos 5x x +=. (1)求sin cos x x -的值;(2)求sin 22cos21tan x x x++的值.针对性训练1、已知θ是第三象限角,且4459sin cos θθ+=,那么2sin θ等于 ( ) A、3 B、3- C 、23 D 、23- 2、函数22y sin x x =- ( ) A 、2π B 、π C 、3π D 、4π3、tan70cos10201)- 等于 ( ) A 、1 B 、2 C 、-1 D 、-24、已知46sin (4)4m m mαα-=≠-,则实数m 的取值范围是______。
高一数学三角函数试题答案及解析

高一数学三角函数试题答案及解析1.在中,求证:.【答案】见解析【解析】证明:,同理可得,,.【考点】本题主要考查余弦定理、半角公式。
点评:涉及三角不等式的证明问题,往往要考虑三角函数的单调性、有界性,本题利用“放缩”思想,达到证明目的。
2.在中,求证:.【答案】见解析【解析】证明:,同理可得,,.【考点】本题主要考查余弦定理、半角公式。
点评:涉及三角不等式的证明问题,往往要考虑三角函数的单调性、有界性,本题利用“放缩”思想,达到证明目的。
3.函数y=tan x是A.周期为π的偶函数B.周期为π的奇函数C.周期为π的偶函数D.周期为π的奇函数【答案】B【解析】函数定义域关于原点对称,且,所以函数为奇函数;又因为=tan x,所以周期为π,故选B。
【考点】本题主要考查三角函数的性质。
点评:简单题,利用周期函数、奇偶函数的定义判断。
4.已知θ角终边上一点M(x,-2),,则sinθ=____________;tanθ=____________.【答案】【解析】由三角函数定义,所以=3,,故sinθ=,tanθ=。
【考点】本题主要考查任意角的三角函数定义、同角公式。
点评:待定系数法的应用,分类讨论思想的应用,常考题型5.设(m>n>0),求θ的其他三角函数值.【答案】见解析。
【解析】∵m>n>0,∴>0∴θ是第一象限角或第四象限角.当θ是第一象限角时:sinθ==tanθ=当θ是第四象限角时:sinθ=-tanθ=【考点】本题主要考查任意角的三角函数同角公式。
点评:运用了平方关系求值时,要特别注意讨论开方运算中正负号的选取。
6.化简:2-sin221°-cos 221°+sin417°+sin217°·cos 217°+cos 217°【答案】2【解析】原式=2-(sin221°+cos 221°)+sin217°(sin217°+cos 217°)+cos 217°=2-1+sin217°+cos 217°=1+1=2【考点】本题主要考查任意角的三角函数同角公式。
6-三角函数的化简与求值(练习)

值为1,求常数a的值.
【解析】f(x)=sin(x+ )+sin(x- )+cos x+a
6 6
= 3 sin x+cos x+a=2sin(x+ )+a.
6
由a+2=1,得a=-1.
1.三角函数的求值类型有三类 (1)给角求值:一般所给出的角都是非特殊角,要观察所给角 与特殊角之间的关系,利用三角变换消去非特殊角,转化为求 特殊角的三角函数值问题;
3 6 3 3
(2)化简
2 2 tan α tan 2α + 3 (sin α-cos α). tan 2α tan α
【分析】此三角函数式出现两类函数,利用两角和与差公式 统一函数成为化简的主要目标. 【解析】(1)sin(3x+ )cos(x- )+cos(3x+ )cos(x+ )
3 6 3 3
4 2 4
3
由sin(β- )= ,知cos(β- )=- , 4 13 4 13
cos(α+ )=cos [(α+β)-(β- )]
4 4
12
5
=cos(α+β)cos(β- )+sin(α+β)sin(β- )
4 4
= ×(- )+(- )× =- .
4 5
5 13
3 5
(2)给值求值:给出某些角的三角函数式的值,求另外一些角
的三角函数值,解题的关键在于“变角”,如α=(α+β)-β,2α=(α +β)+(α-β)等,把所求角用含已知角的式子表示,求解时要注意
2021上海沪教新版高一数学下学期同步练习6.3.1正弦定理详解版(01)

6.3.1正弦定理(作业)一、单选题1.(2020·上海高一课时练习)在ABC 中,2a =,1c =,则C 的取值范围是( ).A .0,6π⎛⎤ ⎥⎝⎦B .,62ππ⎡⎤⎢⎥⎣⎦C .,62ππ⎛⎫ ⎪⎝⎭D .0,2π⎛⎫ ⎪⎝⎭2.(2020·上海高一课时练习)在ABC 中,5a =,45B =,105C =,则b 等于( )A .2B .10C .D .3.(2020·上海高一课时练习)在ABC 中,80a =,100b =,30A ︒=,则B 的解的个数是( ) A .无解B .两个解C .一个解D .不确定4.(2020·上海高一课时练习)在ABC 中,若2C B =,则b 等于( )A .2sin cBB .2cos cBC .2sin cCD .2cos cC5.(2020·上海高一课时练习)在ABC 中,用三个角A ,B ,C 或三条边长a ,b ,c 及外接圆半径R 表示三角形的面积S ,下列式子中正确的是( ) ①4abcS R =;②22sin sin sin =S R A B C ;③sin sin =S aR B C ;④1sin sin sin 2S A B C =. A .①②B .①②③C .①④D .②③6.(2020·上海高一课时练习)在ABC 中,45,60,1︒︒===B C c ,则最小边长等于( ).A B C .12D 7.(2020·上海高一课时练习)已知下列条件解三角形,其中有唯一解的是( ) A .20,28,40︒===a b A B .18,20,150︒===a b A C .20,34,70︒===b c BD .60,50,45︒===b c B8.(2020·上海高一课时练习)在ABC 中,3,30︒===a c A ,则ABCS=_________.9.(2020·上海高一课时练习)在ABC 中,若30,10︒===A a b ,则B =________. 10.(2020·上海高一课时练习)在ABC 中,若3,10,30︒===a b C ,则ABCS=__________.11.(2020·上海高一课时练习)在ABC 中,若20a =,11b =,30B =,则sin A =_________. 12.(2020·上海高一课时练习)半径为1的圆内接三角形的面积为14,则三边之积abc =________.13.(2020·上海高一课时练习)在ABC 中,若45,15,2︒︒===B C b ,则该三角形的最长边等于________.14.(2020·上海高一课时练习)在ABC 中,若30,45,10︒︒===A B a ,则b =________. 15.(2020·上海高一课时练习)ABC 的三内角为A ,B ,C ,且方程2()0+++=Bx A C x B 有两个相等的实数根,若cos cos =a C c A ,则ABC 是________三角形. 16.(2020·上海高一课时练习)若ABC 的外接圆半径为12,则2sin sin b C B c+=_________. 17.(2020·上海高一课时练习)若三角形的三个内角之比为1∶2∶3,则它们所对的边长之比为_______18.(2020·上海高一课时练习)在ABC 中,满足条件4,45a b A ︒===的ABC 的个数是________.19.(2020·上海高一课时练习)在ABC 中,若30,8,︒===A a b ,则ABC 的面积等于_________. 三、解答题20.(2020·安徽宣城市·高一期中)△ABC 中,a =7,c =3,且sin sin C B =35. (1)求b ;21.(2020·广东深圳市·红岭中学高一月考)在ABC ∆中,已知4B π=,c =3C π=,求,,A a b 的值.22.(2020·贵港市覃塘区覃塘高级中学高一月考)(1)等比数列{}n a 中,210S =,315S =,求n S .(2)在ABC ∆中,已知030,2B c b ===,求ABC ∆的面积23.(2020·全国高一专题练习)在ABC ∆中,若cos b a C =,试判断ABC ∆的形状.24.(2019·四川眉山市·仁寿一中高一月考)已知ABC 的内角,,A B C 所对的边分别为,,a b c ,若sin cos a C A =.(1)求角A .(2)若a =2c =,求ABC 的面积.25.(2020·四川成都市·成都外国语学校高一期中(文))在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,满足a b c bc a b c-+=+-. (1)求角A ;(2)若ABC 的外接圆半径为1,求ABC 的面积S 的最大值.26.(2020·四川省成都市盐道街中学高一期中)已知A 、B 、C 为ABC 的三内角,且其对边分别为a 、b 、c ,若cos (2)cos 0a C c b A ++=. (1)求A .(2)若a =4b c +=,求ABC 的面积.27.(2019·四川成都市·成都七中高一月考)已知△ABC 中,,33BAC AB π∠==,BD DC λ=,且ACD ∆. (1)若3λ=,求AC 的长;(2)当线段BC 的长度最小时,求λ的值.28.(2021·江苏省锡山高级中学高一期末)如图,已知正方形ABCD 的边长为1,点P ,Q 分别是边BC ,CD 上的动点(不与端点重合),在运动的过程中,始终保持4PAQ π∠=不变,设BAP α∠=.(1)将APQ 的面积表示成α的函数,并写出定义域; (2)求APQ 面积的最小值.29.(2020·辽河油田第二高级中学高一期中)ABC ∆的内角A ,B ,C 所对边分别为a ,b ,c .已知sinsin()2A Ca b B C +=+. (1) 求B ;(2) 若ABC ∆为锐角三角形,且2c =,求ABC ∆面积的取值范围。
高中数学三角函数专题专项练习(非常好)

高中数学三角函数专题专项练习(非常好)三角函数疑难点解析】一、忽略隐含条件例3:若sinx+cosx-1>0,求x的取值范围。
正解:2sin(x+π/4)>1,由sin(x+π/4)>1/√2得2kπ+π/4<x+π/4<2kπ+3π/4(k∈Z)∴2kπ+π/4<x<2kπ+5π/4(k∈Z),即x∈(2kπ+π/4,2kπ+5π/4)(k∈Z)。
改写后:对于不等式sinx+cosx-1>0,可以化简为2sin(x+π/4)>1.由于sin(x+π/4)>1/√2,所以可以得到2kπ+π/4<x+π/4<2kπ+3π/4(k∈Z)。
进一步化简得到x∈(2kπ+π/4,2kπ+5π/4)(k∈Z)。
二、忽视角的范围,盲目地套用正弦、余弦的有界性例4:设α、β为锐角,且α+β=120°,讨论函数y=cos2α+cos2β的最值。
正解:y=1+(cos2α+cos2β)=1+cos(α+β)cos(α-β)=1-cos(α-β),可见,当cos(α-β)=1时,ymin=0;当cos(α-β)=-1时,ymax=2.分析:由已知得30°<α,β<90°,∴-60°<α-β<60°,则-1<cos(α-β)≤1,∴当cos(α-β)=1,即α=β=60°时,ymin=0,最大值不存在。
改写后:已知α、β为锐角,且α+β=120°,求函数y=cos2α+cos2β的最值。
根据cos2θ=1-2sin2θ和cos(α+β)=cosαcosβ-sinαsinβ,可以得到y=1+(cos2α+cos2β)=1+cos(α+β)cos(α-β)=1-co s(α-β)。
当cos(α-β)=1时,即α=β=60°时,ymin=0,最大值不存在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一三角同步练习6(化简与证明)
一、选择题
1、已知cos α= - 1213 ,α∈(π,2π),则tan α的值是 ( )
A .513
B .512
C .125
D .± 512
2、化简
160tan 112+的结果为 ( )
A .-cos160°
B .cos160°
C .±cos160°
D .-sec160°
3、若是α第二象限角,则1sin 1
tan 2-αα化简的结果是 ( )
A .1
B .-1
C .tan 2α
D .-tan 2α
4、若0cot tan cos cos sin sin 22=++θθθθθθ,则θ不可能是 (
) A .第一、第二、第三象限角 B .第一、第二、第四象限角
C .第一、第三、第四象限角
D .第二、第三、第四象限角
5、如果角θ满足1cos sin =+θθ,那么θθcot tan +的值是 ( )
A .1-
B .0
C .1
D .不存在
6、若θ为二象限角,且2cos 2sin 212sin 2cos θ
θ
θθ
-=-,那么2θ
是
A .第一象限角
B .第二象限角
C .第三象限角
D .第四象限角
7、若2tan =x , 则()()x x x x sin cos cos 3sin 1
--的值为:
A .3-
B .5-
C .3
D .5
8、函数()=x f 1
cos 1tan 2tan 1cos 122-++x x x x 值域中元素的个数是( )
A .1个
B .2个
C .3个
D .4个
二、填空题
1、化简sin 2α+sin 2β-sin 2αsin 2β+cos 2αcos 2β= .
2、化简
40sin 140sin 40
cos 40sin 212---= .
3、若α是第四象限角,化简ααtan 2sec 2-=________________.
4、若αα
ααsin 1sin 1sin 1sin 1+---+ = -2 tan α,则角α的取值范围是 .
三、解答题
1、化简:tan α(cos α-sin α)+
ααααcos 1)tan (sin sin ++.
2、求证:1tan 1tan cos sin cos sin 2122-+=-+ααα
ααα.
3、求证:ααααααααcot tan cos sin 2cot cos tan sin 22+=++.
4、已知cos B = cos θsin A , cos C = sin θsin A ,求证:sin 2A +sin 2B +sin 2C = 2.
参考答案
一、选择题
BABB DCDD
二、填空题
1、1;
2、-1;
3、αtan 1-;
4、
()Z k k k ∈+<<+,22
322ππαππ 三、解答题
1、αsin
2、左边αααααα2222cos sin cos sin 2cos sin -++=()α
ααα222cos sin cos sin -+= =-+=-+=1
tan 1tan cos sin cos sin αααααα右边. 3、
∵()()()ααααααααααcot cos 1tan sin 1cot cos tan sin cot tan 2222-+-=+-+ ααααααααααcos sin 2cos sin sin cos cot sin tan cos 22=+=+= ∴ααααααααcot tan cos sin 2cot cos tan sin 22+=++.
4、
∵A B 222sin cos cos θ=,A C 222sin sin cos θ=,
∴()
A C
B 22222sin sin cos cos cos θθ+=+,
即:A C B 222sin sin 1sin 1=-+-,
∴2sin sin sin 222=++C B A .。
