2018版高中数学苏教版必修二学案:1.2.3 第2课时 直线与平面平行的性质
2018版高中数学苏教版必修二学案:1.2.1平面的基本性质

1章立体几何初步点鲁线、面之间的位置关系1.2.1 平面的基本性质【学习目标】1•掌握平面的表示法,点、直线与平面的位置关系2掌握有关平面的三个公理及三个推论.3•会用符号表示图形中点、线、面之间的位置关系ET问题导学----------------------------知识点一平面的概念思考几何里的“平面”有边界吗?用什么图形表示平面?梳理(1)平面的概念广阔的草原、平静的湖面都给我们以平面的形象•和点、直线一样,平面也是从现实世界中抽象出来的几何概念.一般用水平放置的_____________ 作为平面的直观图(2)平面的画法一个平面被另一个平面遮挡住,为了增强立体感,被遮挡部分用画出来•(3)平面的表示方法平面通常用希腊字母a, 3, 丫••表示,也可以用平行四边形的两个相对顶点的字母表示,如图中的平面a平面AC等.知识点二点、线、面之间的位置关系平面的位置关系,如何用思考直线和平面都是由点组成的,联系集合的观点,点和直线,符号来表示?直线和平面呢?梳理点、直线、平面之间的基本位置关系及语言表达宀护¥方位置大糸付号表示点P在直线AB上P€ AB点C不在直线AB上C?AB点M在平面AC上M € 平面AC点A i不在平面AC内A i?平面AC直线AB与直线BC交于点B AB A BC= B直线AB在平面AC内AB?平面AC直线AA i不在平面AC内AA i?平面AC知识点三平面的基本性质思考1直线I与平面a有且仅有一个公共点P.直线I是否在平面a内?有两个公共点呢?思考2观察下图,你能得出什么结论?思考3 观察正方体 ABCD — A I BQ I D I (如图所示),平面ABCD 与平面BCC i B i 有且只有两个 公共点B 、C 吗?梳理公理(推论)文字语言图形语言 符号语言 作用如果一条直线上的两点在平(1)判定直线在平面A € a公理1 面内,那么这条直B € a内;线上所有的点都?(2)证明点在平面内在这个平面内如果两个平面有一个公共点,那么(1)判断两个平面是它们还有其他公否相交;_J P € a公理2 共点,这些公共点P € J?—(2)判定点是否在直的集合是vl线上;的一条直⑶证明点共线问题线题型探究类型一点、直线、平面之间的位置关系的符号表示例1如图,用符号表示下列图形中点、直线、平面之间的位置关系反思与感悟(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.(2)根据符号语言或文字语言画相应的图形时,要注意实线和虚线的区别跟踪训练1根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:(1)A € a, B? a;⑵I? a, m A a= A, A?l;(3)平面ABD A平面BDC = BD,平面ABC A平面ADC = AC.类型二点线共面例 2 如图,已知:a? a, b? a, a n b= A, P€ b, PQ // a,求证:PQ? afex ~~7引申探究将本例中的两条平行线改为三条,即求证:和同一条直线相交的三条平行直线一定在同一平面内•反思与感悟证明多线共面的两种方法(1) 纳入法:先由部分直线确定一个平面,再证明其他直线在这个平面内(2) 重合法:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合•跟踪训练2已知i i n 12=A, 12n 13= B, i i n C如图所示•求证:直线i i, 12, 13在同一平面内•类型三点共线、线共点问题命题角度1点共线问题例3如图,在正方体ABCD —A i B i C i D i中,设线段A i C与平面ABC i D i交于点Q,求证:B, Q, D i三点共线•反思与感悟证明多点共线通常利用公理2,即两相交平面交线的惟一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,然后证明其他点也在直线上•跟踪训练3 已知△ ABC在平面a外,其三边所在的直线满足AB A a= P, BC A a= Q,AC A a=R,如图所示•求证:P, Q, R三点共线.命题角度2线共点问题例4如图所示,在正方体 ABCD — A I B I C I D I 中,E 为AB 的中点,F 为AA i 的中点•求证:CE 、D i F ,DA 三线交于一点反思与感悟 证明三线共点问题可把其中一条作为分别过其余两条直线的两个平面的交线, 然后再证两条直线的交点在此直线上•此外还可先将其中一条直线看作某两个平面的交线,证明该交线与另两条直线分别交于两点,再证点重合,从而得三线共点跟踪训练4已知:平面 a 3, 丫两两相交于三条直线 丨1, 12, 13,且l i , 12不平行•求证:l i , 12, I 3相交于一点•当堂训练1.用符号表示"点 A 在直线I 上,I 在平面a 外”为 ____________ 2•平面a 3有公共点A ,则a 3有 ______________ 个公共点.3. _______________________________下图中图形的画法正确的是 •(填序号)4. _______________________________________________ 空间两两相交的三条直线,可以确定的平面数是 _____________________________________________ •④平而聖和平面0相交乞直线!征平 面庄内•X 直线【疋平面 1点A 花平⑤三个平面两两相交5.如图,a A b = A , a A c = B , a A d = F , b A c = C , c P d = D , b A d = E ,求证:a , b , c , d共面•七规律与方法•1•解决立体几何问题首先应过好三大语言关,即实现这三种语言的相互转换,正确理解集合 符号所表示的几何图形的实际意义, 恰当地用符号语言描述图形语言, 将图形语言用文字语言描述出来,再转换为符号语言.文字语言和符号语言在转换的时候,要注意符号语言所代表的含义,作直观图时,要注意线的实虚•2•在处理点线共面、三点共线及三线共点问题时初步体会三个公理的作用,突出先部分再整 体的思想.Afi答案精析问题导学知识点一思考没有•水平放置的正方形的直观图梳理(2)正方形的直观图虚线知识点二思考点和直线,平面的位置关系可用数学符号“€”或“?”表示,直线和平面的位置关系,可用数学符号“?”或“ ?”表示.知识点三思考1前者不在,后者在.思考2不共线的三点可以确定一个平面.思考3 不是,平面ABCD与平面BCC i B i相交于直线BC.梳理一个AB? a经过这个公共点aP 3= l且P€ l不在同一条直线上的三点外相交平行题型探究例 1 解在(1)中,aP 3= l, a P a= A, a P 3= B.在⑵中,aP 3= l, a? a, b? 3, a P l = P,b P l = P.(2)直线I在平面a内,直线m与平面a相交于点A,且点A不在直线l上,如图②.跟踪训练1解(1)点A在平面a内,点B不在平面a内,如图①.⑶平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC,如图③.例2证明因为PQ // a,所以PQ与a确定一个平面3,所以直线a? 3,点P€ 3因为P€ b, b? a,所以P€ a又因为a? a,所以a与3重合,所以PQ? a引申探究解已知:a // b / c, l P a= A, l P b= B, l P c= C.求证:a, b, c和I共面.证明:如图,•/ a // b,••• a与b确定一个平面a.•「I Cl a= A, l Cl b= B, •- A€ a, B €a.又T A € I, B € I, .• I? a••• b // c, • b与c确定一个平面3,同理I? 3「•平面a与3都包含I和b,且b C I = B,由公理3的推论知:经过两条相交直线有且只有一个平面,•平面a与平面3重合,•a, b, c和I共面.跟踪训练2证明方法一(纳入平面法)11 C "= A, •-11和12确定一个平面aT' 12C b= B , • B € I2.又■/ I2? a , • B € a■同理可证C € aT B € I3 , C € I3 , • I3? a••直线I i , I2 , I3在同一平面内.方法二(辅助平面法)T I i C I2= A, •• I i和I2确定一个平面aI 2C I3= B , •I2 , I3 确定一个平面3T A € I2 , I2? a, • A € a.「A € I2 , I2? 3 •- A€ 3同理可证 B € a, B € 3 C€ a , C €3•••不共线的三个点A , B , C既在平面a内,又在平面3内,•平面a和3重合,即直线I i , 12, 13在同一平面内.例3证明如图,连结A I B,CD I,6 C显然B €平面A i BCD i,D I€平面A I BCD I.••• BDi?平面A I BCD I.同理BD i?平面ABC I D I.•平面ABC1D1 n 平面A1BCD1=BD1.••• A i C n 平面ABC1D1 = Q , • Q € 平面ABC i D i.又••• A i C?平面A i BCD i,•-Q € 平面A i BCD i.•••Q在平面A i BCD i与ABC i D i的交线上,即Q€ BD i, • B, Q, D i三点共线.跟踪训练3 证明方法一•/ AB n a= P,• P € AB, P€ 平面a又AB?平面ABC, • P €平面ABC.•由公理2可知:点P在平面ABC与平面a的交线上.同理可证Q、R也在平面ABC与平面a的交线上.• P、Q、R三点共线.方法二•/ AP n AR = A,•直线AP与直线AR确定平面APR.又T AB n a= P , AC n a= R,•平面APR n平面a= PR.•/ B € 平面APR, C€ 平面APR,• BC?平面APR.•/ Q € BC, ••• Q € 平面APR.又Q € a,• Q€ PR, ••• P、Q、R三点共线. 例4 证明如图,连结EF, D i C, A1B.••• E为AB的中点,F为AA i的中点,1•- EF 綊2A1B.又••• A i B 綊D i C,1•EF 綊2D i C,•E, F, D i, C四点共面,•- D i F与CE相交,设交点为P.又D i F?平面A i D i DA,CE?平面ABCD ,•P为平面A i D i DA与平面ABCD的公共点. 又平面A i D i DA门平面ABCD = DA,根据公理2,可得P€ DA,即CE、D i F、DA相交于一点.跟踪训练4证明如图,aCl # l i, BQ尸12,aCl Y=丨3.且l i , I2不平行,「•I l与12必相交.设l l Q l2= P ,则P€ l i? a, P € I2? Y• I P € aQ 尸I3,「l 1,l2,l3 相交于一点P.当堂训练1. A€ l,l?a2.无数3.①③④⑤4.1或35. 证明因为A ,B ,C 三点不共线,所以A, B,C 三点确定个平面,设为因为A€a,B€a,所以a? a,因为A€b,C €b,所以b? a,因为B€c,C €c,所以c? a,所以a,b, c 都在a内.因为D€c,E€b,所以D€ a,E€a又因为D € d, E€ d,所以d? a,所以a,b,c,d 共面.。
2018年高中数学 第2章 平面解析几何初步 2.1.3 两条直线的平行与垂直课件12 苏教版必修2

43 4 2
1 6
C
3
●
所以 kAB kCD ,从而 AB CD,
o -4
2
5x
又因为
kBC
3 ( 7) 2
25
13 6
,
kDA
3 4 2 (4)
7 6
-3
●
A
●B
所以 kBC kDA ,从而 BC与 DA 不平行,
因此四边形 ABCD 是梯形.
跟踪练习
根据下列各点的坐标,分别判断各组中直线 AB与 CD 是否平行:
l1 l2 k1 k2 (k1, k2均存在)
(2)当两条直线的斜率都不存在时,那么 它们都与x轴垂直,故两条直线互相平行.
例1
求证:顺次连结 A(2, 3), B(5, 7),C(2,3), D(4, 4)
2
四点所得到的四边形是梯形.
y
证明:因为
D●
k AB
7 (3) 2 52
1 6
, kCD
(1) A(1, 2), B(2,1),C(3, 4), D(1, 1).
kAB 1
kCD
5 4
(2) A(2,3), B(2, 1), C(1, 4), D(1,1);
kAB , kCD 均不存在
(3) A(3, 1), B(1,1),C(3,5), D(5,1); 检验两条直线
1 kAB 2
4x y 11 0
求过点 A(2, 3)且与直线l : x 5 0平行的直线 l1方程.
x20
求过点 A(2, 3)且与直线l : y 6 0 平行的直线 l1方程.
y30
思考:所求的直线方程与已知直线方程形式上 有什么关系?
2018版高中数学苏教版必修二:1.2.3 第4课时 直线与平面垂直的性质

你是我心中最美的风景啊你是我心中最美的风 景啊
19
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
21
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
23
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
24
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
你是我心中最美的风景啊你是我心中最美的风 景啊
32
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
34
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
36
5
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
6
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
7
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
8
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
10
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
第1章 1.2.3 直线与平面的位置关系
第4课时 直线与平面垂直的性质
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
2
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
3
2019年7月7日
你是我心中最美的风景啊你是我心中最美的风 景啊
4
2019年7日
你是我心中最美的风景啊你是我心中最美的风 景啊
12
数学必修2线面平行的判定与性质学案
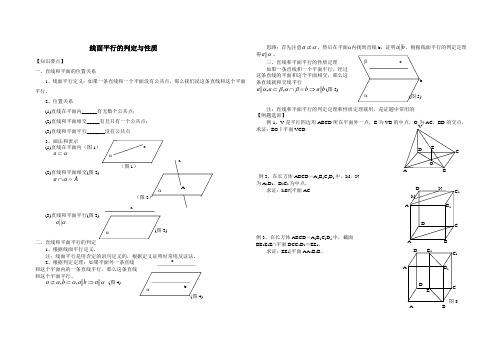
aAα a线面平行的判定与性质【知识要点】一、直线和平面的位置关系1、线面平行定义:如果一条直线和一个平面没有公共点,那么我们说这条直线和这个平面平行。
2、位置关系(1)直线在平面内______有无数个公共点; (2)直线和平面相交_____有且只有一个公共点; (3)直线和平面平行_______没有公共点3、画法和表示(1)直线在平面内(图1)a ⊂α(图1) (2)直线和平面相交(图2) a A ⋂=α(图2)(3)直线和平面平行(图3) a ||α(图3)二、直线和平面平行的判定 1、根据线面平行定义,注:线面平行是用否定的语句定义的,根据定义证明时常用反证法。
2、根据判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线 和这个平面平行。
a b a b a ⊄⊂⇒ααα,,|||| (图4)(图4)思路:首先注意a ⊄α,然后在平面α内找到直线b ,证明a b ||,根据线面平行的判定定理得a ||α。
三、直线和平面平行的性质定理 如果一条直线和一个平面平行,经过 这条直线的平面和这个平面相交,那么这条直线就和交线平行a ab a b ||,,||αβαβ⊂⋂=⇒(图5)(图5)注:直线和平面平行的判定定理和性质定理联用,是证题中常用的 【例题选讲】例1、V 是平行四边形ABCD 所在平面外一点,E 为VB 的中点,O 为AC ,BD 的交点,求证:EO ‖平面VCD例2、在长方体ABCD -A 1B 1C 1D 1中,M ,N 为A 1D 1,D 1C 1为中点,求证:MN||平面AC例3、在长方体ABCD -A 1B 1C 1D 1中,截面BB 1E 1E ⋂平面DCC 1D 1=EE 1,求证:EE 1||平面AA 1B 1B 。
a α ab β α α α a bV D D E C C O BE D E 1 C 1A B 1 A DC BD N C 1M A B 1 A 图8例4、在三棱柱ABC -A 1B 1C 1中, 已知M ,N 分别为A 1B 1 ,B 1C 1 的中点, 求证:M N ||平面AA 1C 1C.例5、一条直线和两个相交平面都平行, 则这条直线和两个平面的交线平行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时 直线与平面平行的性质
学习目标 1.理解直线与平面平行的性质定理.2.掌握直线与平面平行的性质定理,并能应用
定理证明一些简单的问题.
知识点 直线与平面平行的性质定理
思考1 如图,直线l∥平面α,直线a⊂平面α,直线l与直线a一定平行吗?为什么?
思考2 如图,直线a∥平面α,直线a⊂平面β,平面α∩平面β=直线b,满足以上条件的
平面β有多少个?直线a,b有什么位置关系?
梳理
表示
定理
图形 文字 符号
直线与平面平行的性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线______ 错误!
⇒a∥b
类型一 线面平行的性质定理的应用
命题角度1 用线面平行的性质定理证明线线平行)
例1 如图所示,在四棱锥P—ABCD中,底面ABCD是平行四边形,AC与BD交于点O,
M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH.
反思与感悟 (1)利用线面平行的性质定理解题的步骤
①确定(或寻找)一条直线平行于一个平面.
②确定(或寻找)过这条直线且与这个平面相交的平面.
③确定交线.
④由定理得出结论.
(2)常用到中位线定理、平行四边形的性质、成比例线段、平行转移法、投影法等.具体应用时,
应根据题目的具体条件而定.
跟踪训练1 如图,用平行于四面体ABCD的一组对棱AB,CD的平面截此四面体,求证:
截面MNPQ是平行四边形.
命题角度2 用线面平行的性质求线段比
例2 如图,已知E,F分别是菱形ABCD边BC,CD的中点,EF与AC交于点O,点P在
平面ABCD之外,M是线段PA上一动点,若PC∥平面MEF,试求PM∶MA的值.
反思与感悟 破解此类题的关键:一是转化,即把线面平行转化为线线平行;二是计算,把
要求的线段长或线段比问题,转化为同一个平面内的线段长或线段比问题去求解,此时需认
真运算,才能得出正确的结果.
跟踪训练2 如图所示,棱柱ABC—A1B1C1的侧面BCC1B1是菱形,设D是A1C1上的点且
A1B∥平面B1CD,则A1D∶DC1的值为______.
类型二 线线平行与线面平行的相互转化
例3 已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平
面.
反思与感悟 直线和平面的平行问题,常常转化为直线和直线的平行问题,而直线和直线的
平行问题也可以转化为直线与平面的平行问题,要作出命题的正确转化,就必须熟记线面平
行的定义、判定定理和性质定理.
跟踪训练3 如图,在长方体ABCD—A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且
EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.
1.已知a,b表示直线,α表示平面.下列命题中,正确的个数是________.
①若a∥α,b∥α,则a∥b;
②若a∥α,b⊂α,则a∥b;
③若a∥b,b∥α,则a∥α.
2.直线a∥平面α,P∈α,过点P平行于a的直线________.(填序号)
①只有一条,不在平面α内;
②有无数条,不一定在α内;
③只有一条,且在平面α内;
④有无数条,一定在α内.
3.一平面截空间四边形的四边得到四个交点,如果该空间四边形只有一条对角线与这个截面
平行,那么这四个交点围成的四边形是________.
4.如图,在正方体ABCD—A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥
平面AB1C,则线段EF的长度为________.
5.如图,AB是圆O的直径,点C是圆O上异于A,B的点,P为平面ABC外一点,E,F分
别是PA,PC的中点.记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关
系,并加以证明.
1.在遇到线面平行时,常需作出过已知直线与已知平面相交的辅助平面,以便运用线面平行
的性质.
2.要灵活应用线线平行、线面平行的相互联系、相互转化.在解决立体几何中的平行问题时,
一般都要用到平行关系的转化.转化思想是解决这类问题的最有效的方法.
答案精析
问题导学
知识点
思考1 不一定,因为还可能是异面直线.
思考2 无数个,a∥b.
梳理 平行 a⊂β α∩β=b
题型探究
例1 证明 连结MO.
∵四边形ABCD是平行四边形,
∴O是AC的中点.
又∵M是PC的中点,∴AP∥OM.
又∵AP⊄平面BDM,OM⊂平面BDM,
∴AP∥平面BDM.
又∵AP⊂平面APGH,
平面APGH∩平面BDM=GH,
∴AP∥GH.
跟踪训练1 证明 因为AB∥平面MNPQ,平面ABC∩平面MNPQ=MN,且AB⊂平面ABC,
所以由线面平行的性质定理,知AB∥MN.
同理AB∥PQ,
所以MN∥PQ.同理可得MQ∥NP.
所以截面MNPQ是平行四边形.
例2 解 如图,连结BD交AC于点O1,连结OM,因为PC∥平面MEF,
平面PAC∩平面MEF=OM,
所以PC∥OM,所以PMPA=OCAC,
在菱形ABCD中,
因为E,F分别是边BC,CD的中点,所以OCO1C=12.
又AO1=CO1,
所以PMPA=OCAC=14,
故PM∶MA=1∶3.
跟踪训练2 1
例3 已知 如图,直线a、b,平面α,且a∥b,a∥α,a、b都在平面α外.
求证 b∥α.
证明 过a作平面β,使它与平面α相交,交线为c.
因为a∥α,a⊂β,α∩β=c,所以a∥c,
因为a∥b,所以b∥c,
又因为c⊂α,b⊄α,所以b∥α.
跟踪训练3
证明 因为EH∥A1D1,A1D1∥B1C1,EH⊄平面BCC1B1,
B1C1⊂平面BCC1B1,
所以EH∥平面BCC1B1.
又平面FGHE∩平面BCC1B1=FG,
所以EH∥FG,即FG∥A1D1.
又FG⊄平面ADD1A1,
A1D1⊂平面ADD1A1,
所以FG∥平面ADD1A1.
当堂训练
1.0 2.③ 3.梯形 4.2
5.解 直线l∥平面PAC.
证明如下:
因为E,F分别是PA,PC的中点,
所以EF∥AC.
又EF⊄平面ABC,且AC⊂平面ABC,
所以EF∥平面ABC.
而EF⊂平面BEF,且平面BEF∩平面ABC=l,
所以EF∥l.
因为l⊄平面PAC,EF⊂平面PAC,
所以l∥平面PAC.
