几种假设检验Excel实现共68页文档
用Excel进行参数的假设检验
用Excel进行参数的假设检验
计算机应用Excel检验参数假设的第五次实践
假设检验是先对总体的参数或分布形式提出假设，然后利用样本数据信息判断原始假设是否合理，从而决定是接受还是拒绝原始假设。
假设检验的一般步骤是:(1)建立原始假设H0和替代假设H1；
(2)确定适当的测试统计量及其分布，并根据给定的样本值计算测试统计量的值；(3)根据显著性水平？，确定检查阈值和拒绝域；(4)统计判断:如果p值≤,则从样本值中确定概率p值。
或者统计值落在拒绝域内，原始假设H0被拒绝，替代假设H1被接受，即差异在统计上是显著的；如果p值>？或者统计值不在拒绝域内，则接受原始假设H0，即差异在统计上不显著。
下表总结了正常人群参数检验的主要步骤和结果。
表5-1正态总体参数假设检验总结
最初的假设是H0？=？0(？已知)？=？0(？2未知)替代假说H1？≦?0(双边)？>？0(一侧)？？0(一侧)？。
试验三用Excel进行假设检验
8.在单元格B11中输入“ 分布的双侧分位数”，在单
元格C11中输入公式： ，回车后得到 的 t分布的双侧分位数
9
。
9.计算允许误差。在单元格B12中输入“允许误差”， 在单元格C12中输入公式：
，回车后得到的结果为717.6822943。
10.计算置信区间下限。在单元格B13中输入“置信下 限”，在单元格C13中输入置信区间下限公 式： ，回车后得到的结果为40399.19271。 11.计算置信区间上限。在单元格B14中输入“置信上
2
2 假设检验的基本步骤 （1）提出假设H0和HA （2）确定显著水平 （3）进行计算 （4）统计推断 （5）结论
3
假设检验和区间估计
• 1、一个正态总体均值的假设检验：方差 已知 • 例1 假设某批矿砂10个样品中的镍含量，经 测定为3.28，3.27，3.25，3.25，3.27，3.24， 3.26，3.24，3.24，3.25（单位：％）。设总 体服从正态分布，且方差为 ，问：在 下能否认 为这批矿砂的平均镍含量为 3.25 。 1 x x n
41250
38970 40187 43175 41010 39265 41872 42654 41287
40200
42550
41095
40680
43500
39775
40400
假设汽车轮胎的行驶里程服从正态分布，均值、方差未 知。试求总体均值 的置信度为0.95的置信区间。
7
1.在单元格A1中输入“样本数据”，在单元格B4中输
1宏的加载从桌面或开始程序里找到microsoftoffice打开excel2003软件从工具里找到加载宏选择分析工具库点击确定从工具栏里看到数据分析2单个样本平均数的假设测验单个样本平均数的假设测验将数据输入以行的格式将数据输入以行的格式将检测值输入另外将检测值输入另外一行与被检测值个数一致一行与被检测值个数一致从工具栏里选择从工具栏里选择数据分析选择数据分析选择tt检验检验双样本异方差检双样本异方差检得到结果
用Excel进行参数的假设检验
上机实习五用Excel进行参数的假设检验假设检验，就是先对总体的参数或分布形式提出假设，再利用样本数据信息来判断原假设是否合理，从而决定应接受还是拒绝原假设。
进行假设检验的一般步骤：(1)建立原假设H0和备择假设H1；(2)确定适当的检验统计量及其分布，并由给定样本值计算检验统计量的值；(3)根据显著性水平α，确定检验临界值和拒绝域；(4) 作出统计判断：由样本值确定概率P值,若P值≤α或者统计量的值落在拒绝域内，则拒绝原假设H0，接受备择假设H1，即差异有统计显著意义；若P值>α或者统计量的值不落在拒绝域内，，就接受原假设H0，即差异无统计显著意义。
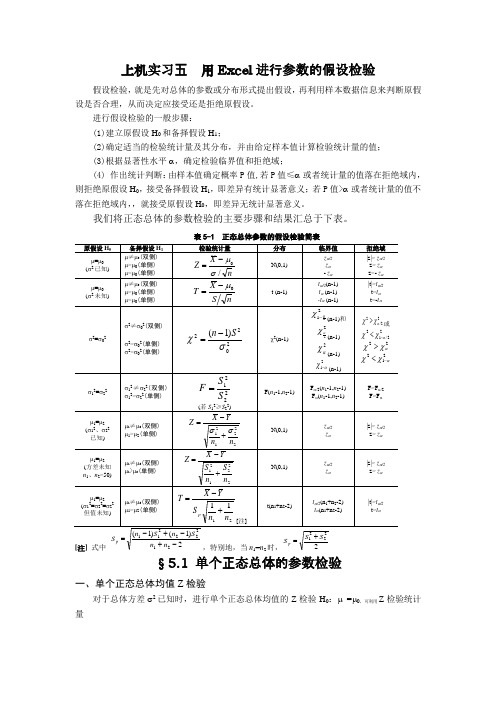
我们将正态总体的参数检验的主要步骤和结果汇总于下表。
表5-1 正态总体参数的假设检验简表§5.1 单个正态总体的参数检验一、单个正态总体均值Z检验对于总体方差σ2已知时，进行单个正态总体均值的Z检验H0：μ=μ0，可利用Z检验统计量n X Z /0σμ-=来进行。
在Excel 中，可利用函数ZTEST 进行，其格式为ZTEST (array, a , sigma) 返回Z 检验的双侧概率P 值P{|Z|>z},n aX Z /σ-=其中 Array 为用来检验的数组或数据区域；a 为被检验的已知均值,即μ0；Sigma 为已知的总体标准差σ，如果省略，则使用样本标准差S 。
例如，要检验样本数据3, 6, 7, 8, 6, 5, 4, 2, 1, 9的总体均值是否等于4，如果已知其总体标准差为2，则只需计算ZTEST({3, 6, 7, 8, 6, 5, 4, 2, 1, 9}, 4，2)，其概率值P=0.0409951<0.05，认为在显著性水平α=0.05下，总体均值与4有显著差异。
如果总体标准差未知，而用样本标准差S 替代时，计算ZTEST({3, 6, 7, 8, 6, 5, 4, 2, 1, 9}, 4)，得到其概率值P =0.090574>0.05,认为在显著性水平α=0.05下，总体均值与4无显著差异。
Excel进行假设检验
使用Excel进行假设检验在假设检验中最常用的检验规则是计算检验统计量的实际值和临界值，通过实际值和临界值的对比得出检验结论；或者计算统计量实际值的p-值，通过p-值和显著性水平α的对比得出结论。
假设检验中使用的数据可以分为两种情况：一是经过统计汇总的数据，已经得到了样本均值和标准差（或者总方差已知）；二是原始数据。
在前一种情况下需要解决的计算问题是计算统计量的临界值，或者根据统计量的实际值计算p-值；在后一种情况下则可以使用统计软件直接得出统计量的临界值和检验的p-值。
top↑检验统计量临界值的计算在已知样本的均值、标准差（或者总方差已知）时，可直接计算出检验统计量的值，然后使用Excel或其他软件计算统计量的临界值，通过实际值与临界值的对比得出检验结论。
用Excel计算统计量的临界值时需要特别注意两个方面的问题。
一是检验的类型：是双侧检验、左侧检验还是右侧检验？双侧检验和单侧检验计算临界值时对显著性水平处理方式不同，双侧检验要求每一侧的尾部面积为α/2，而单侧检验要求在拒绝域一侧的尾部面积为α。
二是在Excel中正态分布、t分布和F分布累积分布反函数中对概率参数的要求不同，注意分清楚这个参数与显著性水平的关系。
[例6.7] 某机器制造的产品厚度应为5厘米。
为了了解机器的性能是否良好，从产品中随机抽取10件，样本均值为5.3厘米，样本标准差为0.3厘米。
已知总体服从正态分布，试以0.05和0.01的显著性水平总体均值是否等于5厘米。
根据题意这里应该使用t统计量。
检验统计量等于。
在这个例子中应该使用双侧检验，95%的临界值在Excel中应该使用公式“=TINV(0.05,9)”计算，结果为2.2622。
99%的临界值为“=TINV(0.01,9)”等于3.2498。
因此，检验的结论是，在0.05显著性水平下拒绝零假设，在0.01的显著性水平不能拒绝零假设。
[例6.8] 一手机厂商声称其某种型号的手机在完全充电的情况下待机时间在150小时以上。
用Excel进行假设检验
用Excel 进行假设检验假设检验包括一个正态总体的参数检验和两个正态总体的参数检验。
对于一个正态总体参数的检验，可利用函数工具和自己输入公式的方法计算统计量，并进行检验。
本例主要介绍如何使用Excel 进行两个正态分布的均值方差的检验。
[资料]为了评价两个学校的教学质量，分别在两个学校抽取样本。
在A 学校抽取30名学生，在B 学校抽取40名学生，对两个学校的学生同时进行一次英语标准化考试，成绩如附表6-1所示。
假设学校A 考试成绩的方差为64，学校B 考试成绩的方差为100。
检验两个学校的教学质量是否有显著差异。
（α＝0.05） 附表6-1 学校A 学校B 70 97 85 87 64 73 86 90 82 83 92 74 72 9476 89 73 88 91 79 84 76 87 8885 78 83 84 91 7476 91 57 62 89 82 9364 80 78 99 59 79 8270 85 83 87 78 84 84 7079 72 91 93 75 85 65 7479 64 84 66 66 85 78 837574假定我们将上表中学校A 的数据输入到工作表中的A2：A31，学校B 的数据输入到工作表的B2：B41。
[步骤]第1步：选择“工具”下拉菜单。
再选择“数据分析”选项。
第2步：在分析工具中选择“Z-检验：双样本平均差检验”，如附图6-1。
附图6-1第3步：当出现对话框后，在“变量1的区域”方框内键入A2：A31；在“变量2的区域”方框内键入B2：B41；在“假设平均差”方框内键入0；在“变量1的方差”方框内键入64；在“变量2的方差”方框内键入100；在“α”方框内键入0.05；在“输出选项”中选择输出区域（在此选择“新工作表”）。
如附图6-2所示。
附图6-2第4步：所有选项设置好，选择确定。
3试验三、用Excel进行假设检验
表5.2 两种密度的稻田亩产(kg)
y1(30万苗) 400 420 435 460 425 y2(35万苗) 450 440 445 445 420
SS2=550
故
1930 550 s 310 44
2 e
s y1 y2
2 310 11.136(kg) 5
y1(喷矮壮素)y2(对照)
160
160 200 160 200 170 150 210
170
270 180 250 270 290 270 230
t-检验: 双样本等方差假设
变量 1 平均 方差 观测值 合并方差 假设平均差 176.25 541.0714 8 1479.167 0
变量 2 233.3333 2300 9
d
为：
sd
因而
(d d )2 n(n 1)
d d t sd
它具有 v =n－1。若假设 H 0:μd 0，则上式改为：
t d sd
即可测验 H 0:μd 0
[例3] 选生长期、发育进度、植株大小和其他方面皆比
较一致的两株番茄构成一组，共得7组，每组中一株接种A处
理病毒，另一株接种B处理病毒，以研究不同处理方法的饨 化病毒效果，表5.4结果为病毒在番茄上产生的病痕数目，试 测验两种处理方法的差异显著性。 这是配对设计，因A、 B两法对饨化病毒的效 应并未明确，故用两尾 测验。
170
df
t Stat P(T<=t) 单尾 t 单尾临界 P(T<=t) 双尾 t 双尾临界
15
-3.05452 0.004015 1.75305 0.008029 2.13145
专题3 几种假设检验的Excel实现sktg11
差异显著性检验
差异显著性检验
可以用两种方法来判定检验的结果： (1) 临界值检验法：这是t双边检验问题，将上述图形 中t统计量的观测值“t Stat”与“t双尾临界值”进行 比较，现在t统计量的观测值0.280，它小于t双尾临界 值2.101，所以在显著性水平0.05下接受原假设（即： 没有显著性差异）。 (2) P值检验法：此双边检验问题的P值为0.783，大于 显著性水平alpha（=0.05），故接受原假设（即：没 有显著性差异） 。
信息技术与数学教学
第十一讲
几种假设检验的Excel实现
差异显著性检验
1. 教育统计理论基础 2. 在Excel软件中的实现
3. 实际应用实例与Excel解答
差异显著性检验
1. 假设检验的基本原理 零假设（虚无假设）：是关于当前样本所属的总体（指 参数）与假设总体（指参数）无区别的假设，一般H0表 示。 备择假设（研究假设）：是关于当前样本所属的总体 （指参数）与假设总体（指参数）相反的假设，一般用 H1表示。 由于直接检验备择假设的真实性困难，假设检验一般都 是从零假设出发，通过零假设的不真实性来证明备假设 的真实性。
差异显著性检验
6.单样本Z检验
单样本数容量不小于30时，要用Z检验（有的教材也 称为U检验）
三个例子（双侧检验、左侧检验、右侧检验各一例）
差异显著性检验
例12：某小学历届毕业生汉语拼音测 试平均分数为66分，标准差为11.7。 现以同样的试题测试应届毕业生（假 设应届与历届毕业生条件基本相同）， 并从中随机抽36份试卷，算得平均 分为69分，问该校应届与历届毕业 生汉语拼音测试成绩是否有显著性差 异？
（1）提出假设 零假设H0：μ1=μ2（实验班和对照班样本来自同一 个总体）。 备择假设H1：μ1≠μ2 （实验班和对照班样本不是来 自同一个总体）。 （2）选择统计量，计算其值
[实训]用Excel进行假设检验
![[实训]用Excel进行假设检验](https://img.taocdn.com/s3/m/9c4c6f2fa6c30c2259019e85.png)
[实训四]假设检验一、简介：假设检验是统计推断中的重要内容。
以下例子利用Excel的正态分布函数NORMSDIST、判断函数IF 等，构造一张能够实现在总体方差已知情况下进行总体均值假设检验的Excel 工作表。
二、操作步骤：1．构造工作表。
如图附-15 所示，首先在各个单元格输入以下的内容，其中左边是变量名，右边是相应的计算公式。
2. 为表格右边的公式计算结果定义左边的变量名。
选定A3:B4,A6:B8，A10:A11,A13:A15 和A17:B19 单元格，选择“插入”菜单的“名称”子菜单的“指定”选项，用鼠标点击“最左列”选项,然后点击“确定”按扭即可。
图附-153．输入样本数据，以及总体标准差、总体均值假设、置信水平数据。
如图附-16 所示。
4．为样本数据命名。
选定C1:C11 单元格，选择“插入”菜单的“名称”子菜单的“指定”选项，用鼠标点击“首行”选项,然后点击“确定”按扭，得到如图附-16 中所示的计算结果。
图附-16三、结果说明：如图附-16 所示，该例子的检验结果不论是单侧还是双侧均为拒绝Ho 假设。
所以，根据样本的计算结果，在5%的显著水平之下,拒绝总体均值为35 的假设。
同时由单侧显著水平的计算结果还可以看出，在总体均值是35 的假设之下，样本均值小于等于31.4 的概率仅为0.020303562。
四、双样本等均值假设检验（一）简介：双样本等均值检验是在一定置信水平之下,在两个总体方差相等的假设之下，检验两个总体均值的差值等于指定平均差的假设是否成立的检验。
我们可以直接使用在Excel 数据分析中提供双样本等均值假设检验工具进行假设检验。
以下通过一例说明双样本等均值假设检验的操作步骤。
例子如下，某工厂为了比较两种装配方法的效率，分别组织了两组员工，每组9 人，一组采用新的装配方法，另外一组采用旧的装配方法。
18个员工的设备装配时间图附-17 中表格所示。
根据以下数据，是否有理由认为新的装配方法更节约时间？图附-17（二）操作步骤：以上例子可按如下步骤进行假设检验。