各地名校试题解析分类汇编(一)理科数学：3导数1

合集下载

2013年高考真题理科数学解析分类汇编3-导数

2013年高考真题理科数学解析分类汇编3 导数一选择题1.四川10．设函数()f x =（a R ∈，e 为自然对数的底数）．若曲线sin y x =上存在00(,)x y 使得00(())f f y y =，则a 的取值范围是（）（A ）[1,]e （B ）1[,1]e - （C ）[1,1]e + （D ）1[,1]e e -+答案：A【解析】：都是增函数所以()f x =增函数，所以有反函数，又00(())f f y y =⟹又即⟹，又与关于直线对称所以的解一定在直线上即说明与直线在区间上有交点！即方程在区间上有解⟺在区间上有解 ⇔在区间上有解下面来研究函数在区间的值域=0⇒, x, x≥=3−2>0因此在区间上是增函数，所以即所以2.安徽理（10）若函数有极值点1x ，2x ，且11()=f x x ，则关于x 的方程3的不同实根个数是（A ）3 （B ）4 （C ） 5 （D ）6 【答案】 A沈阳马老师解答，版权所有【马老师解析】3=0有两个解，1x ，2x ，不妨设1x <2x ，所以3⟺,11()=f x x 为极大值点，x ∈(−∞,) 所以方程有两个解，, 有一个解，所以选A3. [新课标I]16、若函数()f x =22(1)()x x ax b -++的图像关于直线x =－2对称，则()f x 的最大值是______.【命题意图】本题主要考查函数的对称性及利用导数求函数最值，是难题. 【解析】由()f x 图像关于直线x =－2对称，则 0=(1)(3)f f -=-=22[1(3)][(3)3]a b ----+，0=(1)(5)f f =-=22[1(5)][(5)5]a b ----+，解得a =8，b =15， ∴()f x =22(1)(815)x x x -++，∴()f x '=222(815)(1)(28)x x x x x -+++-+=324(672)x x x -++-=4(2)(22x x x -++++当x ∈(－∞,2--∪(－2, 2-+时，()f x '＞0，当x ∈(2--－2)∪(2-+∞)时，()f x '＜0，∴()f x 在（－∞，2-）单调递增，在（2-2）单调递减，在（－2，2-单调递增，在（2-++∞）单调递减，故当x =2-x =2-时取极大值，(2f -=(2f -+=16.4.新课标II 10、已知函数32()f x x ax bx c =+++，下列结论中错误的是（）（A ）0x R ∃∈，0()0f x =（B ）函数()y f x =的图象是中心对称图形（C ）若0x 是()f x 的极小值点，则()f x 在区间0(,)x -∞单调递减（D ）若0x 是()f x 的极值点，则0'()0f x = 【答案】C【解析】若0c =则有(0)0f =，所以A 正确。

2019年高考真题和模拟题分项汇编数学(理)：专题03 导数及其应用 (含解析).docx

专题03导数及其应用1. [2019年高考全国III 卷理数】已知曲线y = ae x +xlnx 在点(1, ae)处的切线方程为y=2x+b,贝9 A. a = e, b = —1 B. a=e, b=l C. a — e _1, b = lD. a = e"1 > b = -\【答案】D【解析】T y' = ae* + lnx+l,切线的斜率 k = y' |Y=1= ae+1 = 2,a = e _1，将(1,1)代入 y = 2x + b,得 2 + b = l,b = -l. 故选D.【名师点睛】本题求解的关键是利用导数的几何意义和点在曲线上得到含有a, b 的等式，从而求解，属于常考题型.了2 O XTTV 2d V* V 12. [2019年高考天津理数】已知tzeR ，设函数/(%)=' _ '若关于X 的不等式/(x)>0在R 上x-alnx, x>l.恒成立，则a 的取值范围为A. [0,1]B. [0,2]C. [0,e]D. [l,e]【答案】C【解析】当兀=1时，/(1) = 1 —2a + 2a = l>0恒成立;当 x<l 时，/(%) = x 2-2ajc + 2a>0^ 2a>^-恒成立,x-1令g(x) =—7x-1(1 —兀―1)2_ (1—兀)2—2(1 —兀)+ 1 1 — X 1 — X当1 —兀=丄，即x = 0时取等号,1-X贝0g(x) = ——1-X2a= 0,则a>0.Y当 x 〉l 时，f(x) = x-a\nx>0,即a< ---------------- 11 成立,lnx当x>e 时,h'(x) >0,函数〃(x)单调递增, 当0<x<e 时，h'(x) <0,函数力(x)单调递减, 则x = e 时，〃(x)取得最小值A(e) = e,•■- a<h(x)nin =e,综上可知，a 的取值范围是［0,e ］. 故选C.【名师点睛】本题考查分段函数的最值问题，分别利用基本不等式和求导的方法研究函数的最值，然后解决恒成立问题.x,x<03. (2019浙江)已知a,bwR ，函数/(%) = < 1 1 2.若函数f(x)-ax-b 恰有3个零点, —X ——(Q + 1)兀 + ax, X > 0 13 2A. a<-\, b<0 C. tz>—1, Z?<0D. a>—1, Z?>0【答案】C【解析】当 x<0 时，y=f (x) -ax - b=x - ax - b= (1 - a) x - b=0,得 x= 丿丿 l-a则y=f (x) -ax-b 最多有一个零点；当 x>0 时，y=f (兀)-ax - b= -x 3—- (a+1) x^+ax - ax - b= -x 3—- (a+1) x 2 - b, —)J3 2 3 2y = x 2-(€l + l)x,当 a+lwo,即來-1 时，y>0, y=f (x) -ax-b 在［0, +oo)上单调递增，则y =f -ax-b 最多有一个零点，不合题意；当a+l>0,即°>-1时，令y'>0得兀丘@+1, +oo),此时函数单调递增，令WVO 得用［0, d+1),此时函数单调递减，则函数最多有2个零点.根据题意，函数y=f (x) -ax-b 恰有3个零点o 函数y=f (x) - ax - b 在(-oo, 0)上有一个零点，在［0, +oo)令〃(x)=—, lnx则 h\x)=lnx-1(In x)2 B. a<-l, b>0上有2个零点,如图：b—b>01-a (a + l)3 - j (a + l)(a + l)2- b<0解得b<0, 1 - a>0, b> -- (a+1) 3,6则a>-l, b<0.故选C・【名师点睛】本题考查函数与方程，导数的应用.当兀V0时，y=f (x) -ax - b=x - ax - b= (l-°) x~ b最多有一个零点；当空0时，y=/(x) -ax-b=^-\ (a+1) - b,利用导数研究函数的单调性，根据单调性画出函数的草图，从而结合题意可列不等式组求解.4.[2019年高考全国I卷理数】曲线y = 3(x2+x)e x在点(0,0)处的切线方程为_________________ .【答案】3x-y-0【解析】y = 3(2x+l)e A + 3(x2 + x)e r = 3(x2 +3x+l)e r,所以切线的斜率k = y' |x=0=3,则曲线y = 3(x2 + x)^在点(0,0)处的切线方程为y = 3x,即3x — y = 0 .【名师点睛】准确求导数是进一步计算的基础，本题易因为导数的运算法则掌握不熟，而导致计算错误•求导要“慢”, 计算要准，是解答此类问题的基本要求._ 45.[2019年高考江苏】在平面直角坐标系xOy中，P是曲线y = x + —(无>0)上的一个动点，则点P到直线x+ y = 0的距离的最小值是一▲•【答案】44 4【解析】由y = x （x〉0）,得丁' = 1 ——,X X4 4设斜率为一1的直线与曲线_y = x + -（x>0）切于（x0,x0+—）,x 勺由1一一 =一1得x0 = A/2（x0=-A/2舍去），x o曲线y = x + -（x>o）±,点P（V2,3A/2）到直线x+y = o的距离最小，最小值为故答案为4 .【名师点睛】本题考查曲线上任意一点到己知直线的最小距离，渗透了直观想象和数学运算素养.采取导数法，利用数形结合和转化与化归思想解题.6.[2019年高考江苏】在平面直角坐标系中，点A在曲线y=lnr上，且该曲线在点A处的切线经过点（-e, -l）（e 为自然对数的底数），则点A的坐标是▲.【答案】（e, 1）【解析】设出切点坐标，得到切线方程，然后求解方程得到横坐标的值，可得切点坐标.设点A（x0,y0）,则y Q =lnx0.又# =丄，X则曲线y = InX在点A处的切线为y - ％=丄（X —勺），即yin”。

【2013备考】各地名校试题解析分类汇编(一)理科数学：3导数3

各地解析分类汇编：导数31.【云南省玉溪一中2013届高三第三次月考理】（本小题满分12分）已知函数2()()xkf x x k e =-. (1)求()f x 的单调区间；(2)若对(0,)x ∀∈+∞，都有1()f x e≤，求k 的取值范围。

【答案】解：(1)/221()()xk f x x k e k =-，令/()0f x =得x k =±当0k >时，()f x 在(,)k -∞-和(,)k +∞上递增，在(,)k k -上递减；当0k <时，()f x 在(,)k -∞和(,)k -+∞上递减，在(,)k k -上递增(2) 当0k >时，11(1)k kf k ee ++=>；所以不可能对0(∈∀x ，)∞+都有e xf 1)(≤；当0k <时有（1）知()f x 在(0,)+∞上的最大值为24()k f k e -=，所以对0(∈∀x ，)∞+都有e x f 1)(≤即241102k k e e ≤⇒-≤<，故对0(∈∀x ，)∞+都有e x f 1)(≤时，k 的取值范围为1[,0)2-。

2.【云南省玉溪一中2013届高三第四次月考理】（本题12分）（Ⅰ）已知函数ax x x x f -+=ln )(2在)1,0(上是增函数,求a 的取值范围;（Ⅱ）在（Ⅰ）的结论下,设1)(2--=x xae e x g ，∈x []3ln ,0,求)(x g 的最小值.【答案】解:（1）a x x x f -+='12)(,∵f （x ）在（0，1）上是增函数,∴2x+x1-a ≥0在（0,1）上恒成立,即a ≤2x+x 1恒成立, ∴只需a ≤（2x+x1）min 即可. …………4分 ∴2x+x 1≥22 （当且仅当x=22时取等号） , ∴a ≤22 …………6分（2）设[][].3,1,3ln ,0,∈∴∈=t x t e x设)41()2(1)(222a a t at t t h +--=--= ，其对称轴为 t=2a，由（1）得a ≤22， ∴t=2a ≤2＜23…………8分则当1≤2a ≤2,即2≤a ≤22时,h （t ）的最小值为h （2a）=-1-42a ,当2a＜1,即a ＜2时，h （t ）的最小值为h （1）=-a …………10分当2≤a ≤22时g （x ）的最小值为-1-42a , 当a ＜2时g （x ）的最小值为-a. …………12分3.【云南省玉溪一中2013届高三上学期期中考试理】（本小题满分13分）设函数322()(0)f x x ax a x m a =+-+>（Ⅰ）求函数f(x)的单调区间；（Ⅱ）若函数f(x)在x ∈[－1，1]内没有极值点，求a 的取值范围；（Ⅲ）若对任意的a ∈[3,6]，不等式()1f x ≤在x ∈[－2,2]上恒成立，求m 的取值范围.【答案】解：（Ⅰ）∵f ′(x )=3x 2+2ax －a 2=3(x －3a)(x +a ), 又a >0，∴当x <－a 或x >3a时f ′(x )>0；当－a <x <3a时，f ′(x )<0. ∴函数f(x)的单调递增区间为（－∞，－a ），(3a，+∞)，单调递减区间为 (－a ，3a).(4分）（Ⅱ）由题设可知，方程f ′(x )=3x 2+2ax －a 2=0在[－1，1]上没有实根∴⎪⎩⎪⎨⎧><'<-'00)1(0)1(a f f ，解得a >3. （8分）（Ⅲ）∵a ∈[3,6]，∴由（Ⅰ）知3a∈[1，2]，－a ≤－3 又x ∈[－2,2]∴f (x )max =max{f (－2),f (2)} 而f (2)－f (－2)=16－4a 2<0f (x )max =f (-2)= －8+4a +2a 2+m （10分）又∵f (x )≤1在[－2，2]上恒成立∴f (x )max ≤1即－8+4a +2a 2+m ≤1 即m ≤9－4a －2a 2,在a ∈[3，6]上恒成立 ∵9－4a －2a 2的最小值为－87∴m ≤－87. （13分）4.【云南师大附中2013届高三高考适应性月考卷（三）理科】（本小题满分12分）已知f (x) =xlnx.（I ）求f (x) 在[t ，t+2]（t>0）上的最小值；（Ⅱ）证明：(0,)x ∀∈+∞都有121x nx e ex>-。

2021-2022年高考数学分项汇编专题03 导数(含解析)理

2021-2022年高考数学分项汇编专题03 导数（含解析）理一．基础题组1. 【xx新课标，理8】设曲线y=a x-ln(x+1)在点(0,0)处的切线方程为y=2x，则a= （）A. 0B. 1C. 2D. 3【答案】D2. 【xx全国2，理22】(本小题满分12分)已知，函数．(Ⅰ) 当为何值时，取得最小值？证明你的结论；(Ⅱ) 设在上是单调函数，求的取值范围．（II）当≥0时，在上为单调函数的充要条件是即，解得于是在[-1，1]上为单调函数的充要条件是即的取值范围是二．能力题组1. 【xx课标全国Ⅱ，理10】已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是( )．A．x0∈R，f(x0)＝0B．函数y＝f(x)的图像是中心对称图形C．若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)单调递减D．若x0是f(x)的极值点，则f′(x0)＝0【答案】：C【解析】：∵x0是f(x)的极小值点，则y＝f(x)的图像大致如下图所示，则在(－∞，x0)上不单调，故C不正确．2. 【xx全国，理10】已知函数y＝x3－3x＋c的图象与x轴恰有两个公共点，则c＝( )A．－2或2 B．－9或3 C．－1或1 D．－3或1【答案】 A3. 【xx课标全国Ⅱ，理21】(本小题满分12分)已知函数f(x)＝e x－ln(x＋m)．(1)设x＝0是f(x)的极值点，求m，并讨论f(x)的单调性；(2)当m≤2时，证明f(x)＞0.【解析】：(1)f′(x)＝.由x＝0是f(x)的极值点得f′(0)＝0，所以m＝1.于是f(x)＝e x－ln(x＋1)，定义域为(－1，＋∞)，f′(x)＝.函数f ′(x )＝在(－1，＋∞)单调递增，且f ′(0)＝0. 因此当x ∈(－1,0)时，f ′(x )＜0；当x ∈(0，＋∞)时，f ′(x )＞0.所以f (x )在(－1,0)单调递减，在(0，＋∞)单调递增．4. 【xx 新课标，理21】已知函数，曲线y ＝f (x )在点(1，f (1))处的切线方程为x ＋2y －3＝0. (1)求a ，b 的值；(2)如果当x ＞0，且x ≠1时，，求k 的取值范围．【解析】：(1)221(ln )()(1)x a x b x f x x x +-'=-+.由于直线x ＋2y －3＝0的斜率为－，且过点(1，1)，故(1)11(1)2f f =⎧⎪⎨'=-⎪⎩即1122b a b =⎧⎪⎨-=-⎪⎩解得(2)(理)由(1)知，5. 【xx 全国3，理22】（本小题满分12分）已知函数（Ⅰ）求的单调区间和值域；（Ⅱ）设，函数],1,0[],1,0[].1,0[,23)(0123∈∈∈--=x x x a x a x x g 总存在若对于任意使得成立，求a 的取值范围.【解析】：（I ）对函数求导，得222)2()72)(12()2(7164)(x x x x x x x f ----=--+-=' 令解得当变化时，的变化情况如下表：（0，）（，1）1－ 0 +－4－3当时，的值域为[－4，－3].三．拔高题组1. 【xx 新课标，理12】设函数.若存在的极值点满足，则m 的取值范围是（） A. B. C. D. 【答案】C【解析】由题意知：的极值为，所以，因为'0()3cos0x f x mmππ=⋅=，所以，所以即，所以，即3，而已知，所以3，故，解得或，故选C.2. 【xx 全国2，理10】若曲线y ＝x －在点(a ，a －)处的切线与两个坐标轴围成的三角形的面积为18，则a 等于( )A ．64B ．32C ．16D ．8 【答案】：A3. 【xx 全国2，理20】已知函数=.（Ⅰ）讨论的单调性；（Ⅱ）设，当时，,求的最大值；（Ⅲ）已知，估计ln2的近似值（精确到0.001）（Ⅲ）由（Ⅱ）知，32)222(21)ln 22g b b =-+-，当时，32)426ln 202g =->，；当时，2ln(122b b b --=，32)22(322)ln 22g =--，，所以的近似值为.4. 【xx 全国，理20】设函数f (x )＝ax ＋cos x ，x ∈[0，π]． (1)讨论f (x )的单调性；(2)设f (x )≤1＋sin x ，求a 的取值范围．令g(x)＝sin x－x(0≤x≤)，则g′(x)＝cos x－.当x∈(0，arccos )时，g′(x)＞0，当x∈(arccos，)时，g′(x)＜0.又g(0)＝g()＝0，所以g(x)≥0，即x≤sin x(0≤x≤)．当a≤时，有f(x)≤x＋cos x.①当0≤x≤时，x≤sin x，cos x≤1，所以f(x)≤1＋sin x；②当≤x≤π时，f(x)≤x＋cos x＝1＋(x－)－sin(x－)≤1＋sin x. 综上，a的取值范围是(－∞，]．5. 【xx全国2，理22】设函数f(x)＝1－e－x.(1)证明当x＞－1时，f(x)≥；(2)设当x≥0时，f(x)≤，求a的取值范围．(ⅰ)当0≤a≤时，由(1)知x≤(x＋1)f(x)，h′(x)≤af(x)－axf(x)＋a(x＋1)f(x)－f(x)＝(2a－1)·f(x)≤0，h(x)在[0，＋∞)上是减函数，h(x)≤h(0)＝0，即f(x)≤.(ⅱ)当a＞时，由(ⅰ)知x≥f(x)，h′(x)＝af(x)－axf(x)＋ax－f(x)≥af(x)－axf(x)＋af(x)－f(x)＝(2a－1－ax)f(x)，当0＜x＜时，h′(x)＞0，所以h(x)＞h(0)＝0，即f(x)＞，综上，a的取值范围是[0，]．6. 【xx全国2，理20】设函数f(x)=(x+1)ln(x+1),若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.7. 【xx高考新课标2，理12】设函数是奇函数的导函数，，当时，，则使得成立的的取值范围是（）A．B．C．D．【答案】A【解析】记函数，则，因为当时，，故当时，，所以在单调递减；又因为函数是奇函数，故函数是偶函数，所以在单调递减，且．当时，，则；当时，，则，综上所述，使得成立的的取值范围是，故选A．【考点定位】导数的应用、函数的图象与性质．8. 【xx高考新课标2，理21】（本题满分12分）设函数．(Ⅰ)证明：在单调递减，在单调递增；（Ⅱ）若对于任意，都有，求的取值范围．【答案】(Ⅰ)详见解析；（Ⅱ）．【考点定位】导数的综合应用．x29334 7296 犖31735 7BF7 篷29503 733F 猿30311 7667 癧20935 51C7 凇934330 861A 蘚@/28163 6E03 渃39157 98F5 飵-s26377 6709 有。

【2013备考】各地名校试题解析分类汇编(一)理科数学：3导数1

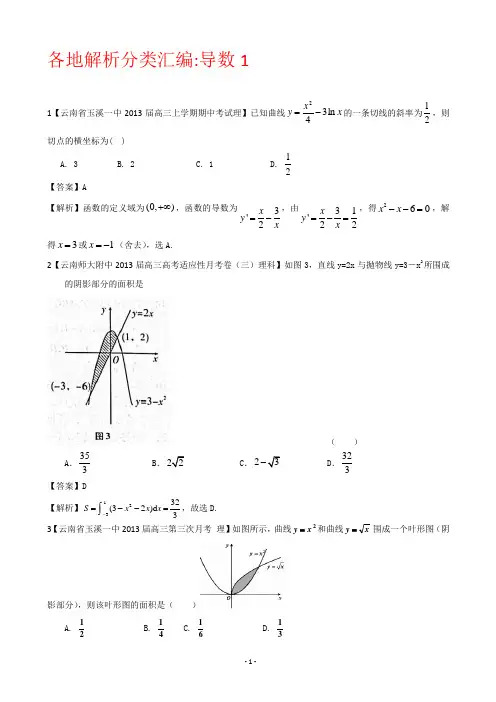
各地解析分类汇编:导数11【云南省玉溪一中2013届高三上学期期中考试理】已知曲线x x y ln 342-=的一条切线的斜率为21，则切点的横坐标为( ) A. 3 B. 2 C. 1 D.21【答案】A【解析】函数的定义域为(0,)+∞，函数的导数为3'2x y x =-，由31'22x y x =-=，得260x x --=，解得3x =或1x =-（舍去），选A.2【云南师大附中2013届高三高考适应性月考卷（三）理科】如图3，直线y=2x 与抛物线y=3－x 2所围成的阴影部分的面积是（）A ．353B ．C ．2D ．323【答案】D【解析】12332(32)d 3S x x x -=--=⎰，故选D. 3【云南省玉溪一中2013届高三第三次月考理】如图所示，曲线2x y =和曲线x y =围成一个叶形图（阴影部分），则该叶形图的面积是（）A.21 B. 41 C. 61 D. 31【答案】D【解析】由2y xy ⎧=⎪⎨=⎪⎩，解得11x y =⎧⎨=⎩或0x y =⎧⎨=⎩，所以根据积分的应用可得阴影部分的面积为3123120021211)()33333x dx x x =-=-=⎰，选D. 4【山东省烟台市莱州一中2013届高三10月月考（理）】由直线2,21==x x ，曲线xy 1=及x 轴所谓成图形的面积为 A.415B.417C.2ln 21D. 2ln 2【答案】D【解析】根据积分的应用可知所求22112211ln ln 2ln2ln 22dx x x==-=⎰，选D. 5【云南师大附中2013届高三高考适应性月考卷（三）理科】已知()f x 为R上的可导函数，且,x R ∀∈均有()f x f>′（x），则有（）A．20132013(2013)(0),(2013)(0)e f f f e f -<> B．20132013(2013)(0),(2013)(0)e f f f e f -<< C．20132013(2013)(0),(2013)(0)e f f f e f ->>D ．20132013(2013)(0),(2013)(0)e f f f e f -><【答案】A【解析】构造函数()()x f x g x=，则2()()()()()()()x x x x f x e e f x f x f x g x e e ''''--==，6【山东省烟台市莱州一中2013届高三10月月考（理）】曲线x e y 21=在点()2,4e处的切线与坐标轴所围三角形的面积为 A.2eB.24eC.22eD.229e 【答案】A【解析】121'2x y e =，所以在点()2,4e 的导数为142211'22y e e ⨯==，即切线斜率为212k e =，所以切线方程为221(4)2y e e x -=-，令0x =得，2y e =-，令0y =，得2x =.所以三角形的面积为22122e e ⨯⨯=，选A.7【云南省昆明一中2013届高三新课程第一次摸底测试理】函数22ln y x x e ==在处的切线与坐标轴所围成的三角形的面积为A ．292e B ．212Se =C ．22eD ．2e【答案】D【解析】212'2y x x x =⨯=，所以在2x e =处的切线效率为22k e =，所以切线方程为2224()y x e e-=-，令0x =，得2y =，令0y =，得2x e =-，所以所求三角形的面积为22122e e ⨯⨯=，选D.8【山东省烟台市莱州一中20l3届高三第二次质量检测（理）】曲线()ln 2y x =+在点()1,0P -处的切线方程是 A.1y x =+ B.1y x =-+C.21y x =+D.21y x =-+【答案】A 【解析】1'2y x =+,所以在点P 处的切线斜率1112k ==-+，所以切线方程为(1)1y x x =--=+，选A.9【山东省烟台市莱州一中20l3届高三第二次质量检测（理）】由直线2,,0sin 33x x y y x ππ====与所围成的封闭图形的面积为 A.12B.1C.2【答案】B【解析】由积分的应用得所求面积为2233332sin cos coscos 2cos 1333xdx xπππππππ=-=-+==⎰，选B. 10【天津市新华中学2012届高三上学期第二次月考理】已知函数))((R x x f ∈满足1)1(=f ，且)(x f 的导函数21)('<x f ，则212)(+<x x f 的解集为 A. {}11<<-x x B. {}1-<x x C. {}11>-<x x x 或 D. {}1>x x【解析】设1()()()22xF x f x =-+, 则11(1)(1)()11022F f =-+=-=，1'()'()2F x f x =-，对任意x R ∈，有1'()'()02F x f x =-<，即函数()F x 在R 上单调递减，则()0F x <的解集为(1,)+∞，即212)(+<x x f 的解集为(1,)+∞，选D.11【山东省烟台市莱州一中20l3届高三第二次质量检测（理）】函数()32f x x bx cx d =+++的大致图象如图所示，则2212x x +等于A.89B.109C.169D.289【答案】C【解析】函数过原点，所以0d =。

【名师解析】高三名校数学理试题分省分项汇编专题03导数版含解析

】设
1 (
x
数项为 a ，则直线 y ax 与曲线 y x 2 围成图形的面积为 ( )
x 2 )3 的展开式的常
27 A.
9 B.
C. ９
27 D.
2
2
4
所以它们围成的图形的面积是：
S
3
3x
x2 dx
0
考点： 1. 二项式定理； 2. 定积分
3 x2 2
1 x3 3
3 0
9. 2
------ 珍贵文档 ! 值得收藏！ ------
a R.
(I) 讨论函数 f ( x) 的单调性；
( Ⅱ) 当 x 1 时， f (x) ≤ ln x 恒成立，求 a 的取值范围． x1
【答案】(I) a 0 ， f x 在 0,
单调递增； a
0 ，f
x在
1 0,
单调递增，
1 ,
a
a
单调递减 .
( Ⅱ） a
1
.
2
【解析】
试题分析： (I) 根据单调函数的性质，分 a 0 ， a 0 讨论 y a( x 1) 的单调性，即可得
) + ... f (
)+ f(
) =(
2013
2013
2013
2013
A. –4025
【答案】 C
B. 4025
C. –8050
)
D. 8050
【解析】
------ 珍贵文档 ! 值得收藏！ ------
------ 精品文档 ! 值得拥有！ ------
3. 【辽宁省抚顺市六校联合体
2014 届高三上学期期中考试理
为自然对数的
------ 珍贵文档 ! 值得收藏！ ------

高考数学各地名校试题解析分类汇编(一)3 导数1 理

各地解析分类汇编:导数11【云南省玉溪一中2013届高三上学期期中考试理】已知曲线x x y ln 342-=的一条切线的斜率为21，则切点的横坐标为( ) A. 3 B. 2C. 1D.21 【答案】A【解析】函数的定义域为(0,)+∞，函数的导数为3'2x y x =-，由31'22x y x =-=，得260x x --=，解得3x =或1x =-（舍去），选A. 2【云南师大附中2013届高三高考适应性月考卷（三）理科】如图3，直线y=2x 与抛物线y=3－x 2所围成的阴影部分的面积是（）A ．353B ．22C ．23-D ．323【答案】D【解析】12332(32)d 3S x x x -=--=⎰，故选D. 3【云南省玉溪一中2013届高三第三次月考理】如图所示，曲线2x y =和曲线x y =围成一个叶形图（阴影部分），则该叶形图的面积是（）A.21 B. 41 C. 61 D. 31 【答案】D【解析】由2y xy ⎧=⎪⎨=⎪⎩11x y =⎧⎨=⎩或00x y =⎧⎨=⎩，所以根据积分的应用可得阴影部分的面积为31231221211)()33333x dx x x =-=-=⎰，选D. 4【山东省烟台市莱州一中2013届高三10月月考（理）】由直线2,21==x x ，曲线xy 1=及x 轴所谓成图形的面积为A.415B.417 C.2ln 21D. 2ln 2【答案】D【解析】根据积分的应用可知所求22112211ln ln 2ln2ln 22dx x x==-=⎰，选D. 5【云南师大附中2013届高三高考适应性月考卷（三）理科】已知()f x 为R 上的可导函数，且,x R ∀∈均有()f x f >′（x ），则有（）A ．20132013(2013)(0),(2013)(0)e f f f e f -<> B ．20132013(2013)(0),(2013)(0)e f f f e f -<< C ．20132013(2013)(0),(2013)(0)e f f f e f ->>D ．20132013(2013)(0),(2013)(0)ef f f e f -><【答案】A【解析】构造函数()()x f x g x e=，则2()()()()()()()x x x xf x e e f x f x f xg x e e ''''--==，是20132013(2013)(0)(2013)(0)e f f f e f -><，，故选A. 6【山东省烟台市莱州一中2013届高三10月月考（理）】曲线x e y 21=在点()2,4e处的切线与坐标轴所围三角形的面积为A.2eB.24eC.22eD.229e 【答案】A【解析】121'2x y e =，所以在点()2,4e 的导数为142211'22y e e ⨯==，即切线斜率为212k e =，所以切线方程为221(4)2y e e x -=-，令0x =得，2y e =-，令0y =，得2x =.所以三角形的面积为22122e e ⨯⨯=，选A. 7【云南省昆明一中2013届高三新课程第一次摸底测试理】函数22ln y x x e ==在处的切线与坐标轴所围成的三角形的面积为A ．292e B ．212Se =C ．22eD ．2e【答案】D 【解析】212'2y x x x =⨯=，所以在2x e =处的切线效率为22k e=，所以切线方程为2224()y x e e-=-，令0x =，得2y =，令0y =，得2x e =-，所以所求三角形的面积为22122e e ⨯⨯=，选D. 8【山东省烟台市莱州一中20l3届高三第二次质量检测（理）】曲线()ln 2y x =+在点()1,0P -处的切线方程是A.1y x =+B.1y x =-+C.21y x =+D.21y x =-+【答案】A 【解析】1'2y x =+,所以在点P 处的切线斜率1112k ==-+，所以切线方程为(1)1y x x =--=+，选A.9【山东省烟台市莱州一中20l3届高三第二次质量检测（理）】由直线2,,0sin 33x x y y x ππ====与所围成的封闭图形的面积为A.12B.1【答案】B 【解析】由积分的应用得所求面积为2233332sin cos coscos 2cos 1333xdx xπππππππ=-=-+==⎰，选B. 10【天津市新华中学2012届高三上学期第二次月考理】已知函数))((R x x f ∈满足1)1(=f ，且)(x f 的导函数21)('<x f ，则212)(+<x x f 的解集为 A. {}11<<-x x B. {}1-<x x C. {}11>-<x x x 或 D. {}1>x x 【答案】D【解析】设1()()()22x F x f x =-+, 则11(1)(1)()11022F f =-+=-=，1'()'()2F x f x =-，对任意x R ∈，有1'()'()02F x f x =-<，即函数()F x 在R 上单调递减，则()0F x <的解集为(1,)+∞，即212)(+<x x f 的解集为(1,)+∞，选D.11【山东省烟台市莱州一中20l3届高三第二次质量检测（理）】函数()32f x x bx cx d=+++的大致图象如图所示，则2212x x +等于A.89B.109C.169D.289【答案】C【解析】函数过原点，所以0d =。

(2019备考)各地名校试题解析分类汇编(一)理科数学：3导数2.doc

(2019备考)各地名校试题解析分类汇编（一）理科数学：3导数21【山东省烟台市2018届高三上学期期中考试理】〔本小题总分值13分〕函数)(ln )(R a xax x f ∈+=.〔1〕求)(x f 的极值；〔2〕假设函数)(x f 的图象与函数1)(=x g 的图象在区间],0(2e 上有公共点，求实数a 的取值范围.【答案】〔1〕)(x f 的定义域为),0(+∞,2)(ln 1)('x a x x f +-=，……2分令0)('=x f 得a e x -=1，当),0(1a e x -∈时，,0)('>x f )(x f 是增函数；当),(1+∞∈-a e x 时，,0)('<x f )(x f 是减函数，∴)(x f 在a e x -=1处取得极大值，11)()(--==a a e e f x f 极大值，无极小值.………………5分〔2〕①当21e e a <-时，即1->a 时，由〔1〕知)(x f 在),0(1a e -上是增函数，在],(21e e a -上是减函数，11max )()(--==∴a a e e f x f ,又当a e x -=时，0)(=x f ，当],0(a e x -∈时，0)(<x f ；当],(2e e x a -∈时，0)(>x f ；)(x f 与图象1)(=x g 的图象在],0(2e 上有公共点，11≥∴-a e ，解得1≥a ，又1->a ，所以1≥a .………9分②当21e e a ≥-时，即1-≤a 时，)(x f 在],0(2e 上是增函数， ∴)(x f 在],0(2e 上的最大值为222)(ea e f +=，所以原问题等价于122≥+ea，解得22-≥e a .又1-≤a ,∴无解.综上，实数a 的取值范围是),1[+∞.……13分2.【山东省实验中学2018届高三第三次诊断性测试理】〔本小题总分值14分〕函数)(x f 的导数b a b f ax x x f ,,)0(,33)('2=-=为实数，21<<a .〔Ⅰ〕假设)(x f 在区间［-1，1］上的最小值、最大值分别为-2、1，求a 、b 的值；〔Ⅱ〕在〔Ⅰ〕的条件下，求经过点）（1,2P 且与曲线)(x f 相切的直线的方程；〔Ⅲ〕设函数x e x x f x F 2]16)('[)(⋅++=，试判断函数)(x F 的极值点个数。

2021届高三名校数学理试题分省分项汇编专题03 导数 Word版含解析

一．基础题组1. 【河北衡水中学2013～2014学年度高三上学期二调高三数学试卷】如果)(x f '是二次函数, 且)(x f '的图象开口向上,顶点坐标为（1,3）, 那么曲线)(x f y =上任一点的切线的倾斜角α的取值范围是（） A ．]3,0(πB ．)2,3[ππC ．]32,2(ππ D ．),3[ππ2. 【唐山市2013-2014学年度高三年级摸底考试】过坐标原点与曲线ln y x =相切的直线方程为.3. 【河南省方城一高2014届高三第一次调研（月考）】若01axdx =⎰，则实数a 的值是.【答案】24. 【河北唐山开滦二中2013~2014学年度第一学期高三年级期中考试】由曲线11+=x y ，x e y =，直线1=x 所围成的区域的面积为___________5. 【河南省南阳市第一中学2014届高三10月月考】dx x ⎰--2|)1|2(＝．6. 【山西省忻州一中康杰中学临汾一中长治二中2014届高三第一次四校联考】(本小题满分12分)设函数32)1()(ax e x x f x+-= (1) 当31-=a 时，求)(x f 的单调区间；(2) 若当0≥x 时，)(x f 0≥恒成立，求a 的取值范围.【答案】（1）单调递增区间为),0(,)0,2(∞+-，单调递减区间为)2,(--∞；（2）a 的取值范围为),1[+∞-.考点：1.利用导数研究函数的单调性；2.利用导数求函数的最值；3.一元二次不等式的解法. 7．【河南省方城一高2014届高三第一次调研（月考）】（本小题满分12分）若22(ln 1),(0)()(ln 1),()x a x x e f x x a x x e ⎧--<<=⎨+-≥⎩，其中a R ∈.（1）当2a =-时，求函数()f x 在区间2[,]e e 上的最大值；（2）当0a >时，若3[1,),()2x f x a ∈+∞≥恒成立，求a 的取值范围.②当1x e ≤≤时，2()ln f x x a x a =-+，'2()2()22a a a f x x x x x x =-=+， 12a≤即02a <≤时，()f x 在区间[1,]e 上为增函数，当1x =时，min ()(1)1f x f a ==+，且此时2(1)()f f e e <=；8. 【河北省高阳中学2014届高三上学期第一次月考】（本小题满分12分）已知函数()ln(1)(1)1f x x k x =---+．（1）当1k =时，求函数()f x 的最大值；（2）若函数()f x 没有零点，求实数k 的取值范围；【答案】(1)max ()(2)0f x f ==；（2）(1,)k ∈+∞. 【解析】试题分析：(1)通过对函数求导，判函数的单调性，可求解函数的最大值，需注意解题时要先写出函数的定义域，切记“定义域优先”原则;(2)将()ln(1)(1)1f x x k x =---+的零点问题转化为(1)1y k x =--与ln(1)y x =-图象交点个数问题，注意函数(1)1y k x =--的图象恒过定点二．能力题组1. 【河南省南阳市第一中学2014届高三10月月考】设函数2()(0)f x ax b a =+≠，若300()3()f x dx f x =⎰，则0x =（）A ．1±B 2C ．3D ．2【答案】C 【解析】试题分析：因为33230031()()9303f x dx ax b dx ax bx a b =+=+=+⎰⎰，2003()33f x ax b =+，所以209333a b ax b +=+，所以203x =，03x =±，选C.考点：微积分基本定理.2. 【河北唐山开滦二中2013~2014学年度第一学期高三年级期中考试】设函数2()()f x g x x =+，曲线()y g x =在点(1,(1))g 处的切线方程为21y x =+，则曲线()y f x =在点(1,(1))f 处切线的斜率为（）A ．2B ．14-C ．4D ．12-3. 【河北省高阳中学2014届高三上学期第一次月考】曲线)x 0sin π≤≤=（x y 与直线y=21围成的封闭图形的面积为（） A ．3 B.3-2 C.3-2π D.3-3π4. 【河南省南阳市第一中学2014届高三10月月考】若曲线321()3f x x x mx =++的所有切线中，只有一条与直线30x y +-=垂直，则实数m 的值等于（） A ．0B ．2C ．0或2D ．35. 【河北省高阳中学2014届高三上学期第一次月考】曲线ln(21)y x =-上的点到直线230x y -+=的最短距离是（）A.5B.25C.35D.06. 【河北衡水中学2013～2014学年度高三上学期二调高三数学试卷】已知函数1()(*)n f x x n N +=∈的图象与直线1x =交于点P ，若图象在点P 处的切线与x 轴交点的横坐标为n x ，则12013log x ＋22013log x ＋…＋20122013log x 的值为（） A ．－1 B ． 20131log 2012- C ．2013log 2012- D ．1 【答案】A 【解析】试题分析：函数的导数为'()(1)nf x n x =+，所以在1x =处的切线斜率为'(1)=1k f n =+，所以切7. 【河北衡水中学2013～2014学年度高三上学期二调高三数学试卷】由曲线sin ,cos y x y x ==与直线0,2x x π==所围成的平面图形(图中的阴影部分)的面积是.8. 【2012-2013学年度南昌市高三第二次模拟测试卷】曲线y =x cos (0≤x ≤23π)与坐标轴所围成的图形面积是________________. 【答案】3 【解析】试题分析：203cos 3sin (3sin )(3sin 0)322S x x πππ===-=⎰.考点：积分求面积.9. 【唐山市2013-2014学年度高三年级摸底考试】（本小题满分12分）已知函数()2ln ()f x x ax a a R =-+∈.（Ⅰ）讨论()f x 的单调性；（Ⅱ）若()0f x ≤恒成立，证明：当120x x <<时，21211()()12(1)f x f x x x x -<--.若0a ≤，'()0f x >，()f x 在(0,)+∞上递增；若0a >，当2(0,)x a∈时，'()0f x >，()f x 单调递增；当2(,)x a∈+∞时，'()0f x <，()f x 单调递减．………………5分（Ⅱ）由（Ⅰ）知，若0a ≤，()f x 在(0,)+∞上递增，又(1)0f =，故()0f x ≤不恒成立．10. 【河北省唐山市2013届高三第二次模拟考试】（本小题满分12分）已知函数R a x a x x x f ∈-=,2ln )(2 （Ⅰ）若()f x 在（0，∞+）单调递减，求a 的最小值（Ⅱ）若()f x 有两个极值点，求a 的取值范围.()f x 单调递减当且仅当'()0f x ≤，即(0,)x ∀∈+∞，ln 1x a x+≥．①11．【河北衡水中学2013～2014学年度高三上学期二调高三数学试卷】（本题12分）已知函数).1,0(ln )(2≠>-+=a a a x x a x f x（1）求函数)(x f 在点))0(,0(f 处的切线方程；（2）求函数)(x f 单调递增区间；（3）若存在]1,1[,21-∈x x ，使得e e x f x f (1)()(21-≥-是自然对数的底数），求实数a 的取值范围.⑶因为存在12,[1,1]x x ∈-，使得12()()e 1f x f x --≥成立，而当[1,1]x ∈-时，12max min ()()()()f x f x f x f x --≤，所以只要max min ()()e 1f x f x --≥即可．又因为x ，()f x '，()f x 的变化情况如下表所示： x (,0)-∞ 0(0,)∞+ ()f x ' -0 +()f x 减函数极小值增函数所以()f x 在[1,0]-上是减函数，在[0,1]上是增函数，所以当[1,1]x ∈-时，()f x 的最小值 12. 【河北省邯郸市2014届高三9月摸底考试数学】（本小题满分12分）已知函数21()2ln(1)2f x ax x x =-++． (1)求函数()f x 的图象在点(0,(0))f 处的切线方程；(2) 当[)0,x ∈+∞时，函数()ln(1)y f x x =-+图象上的点都在0102x y x ≥⎧⎪⎨-≤⎪⎩所表示的平面区域内，求实数a 的取值范围．(i) 当0a =时，()1x g x x -'=+，当0x >时，()0g x '<，函数()g x 在(0,)+∞上单调递减，故()(0)0g x g ≤=成立． …………8分13. 【河北唐山开滦二中2013~2014学年度第一学期高三年级期中考试】（本小题满分12分）设函数1()(10)(1)ln(1)f x x x x x =>-≠++且. ⑴求函数()f x 的单调区间；⑵求函数()f x 的值域； ⑶已知()mx x 1211+>+对()0,1-∈∀x 恒成立，求实数m 的取值范围. 【答案】（1）详见解析；（2）(]()+∞-∞-,0, e ；（3）ln 2m e >-.【解析】试题分析：（1）判断函数的单调区间，一般利用其导数的符号判断，使导函数为正的区间是增区间，使函数为负的区间是减区间；（2）函数的值域则可利用（1）中得到的函数的单调性进行求解；（3）恒成立问题则常用分离参数的方法，转化为求函数的最值问题，而求函数的最值则仍可利用导数去判断函数的单调性.试题解析：⑴()()()()22ln 111ln 1x f x x x ++'=-++，由()0f x '>解得111x e-<<-，三．拔高题组1. 【山西省忻州一中康杰中学临汾一中长治二中2014届高三第一次四校联考】已知函数)(x f y =定义域为),(ππ-，且函数)1(+=x f y 的图象关于直线1-=x 对称，当),0(π∈x 时，x x f x f ln sin )2()(ππ-'-=，（其中)(x f '是)(x f 的导函数），若)91(log ),3(log ),3(33.0f c f b f a ===π，则c b a ,,的大小关系是( ) A. c b a >> B. c a b >> C.a b c >> D. b a c >>【答案】B【解析】试题分析：因为(1)y f x =+是将()y f x =的图象向左平移1个单位得到，而其图象关于直线1x =-对称，故()y f x =的图象关于y 轴对称，可见()y f x =为偶函数，又2. 【河南省南阳市第一中学2014届高三10月月考】已知曲线方程2()sin 2()f x x ax a R =+∈，若对任意实数m ，直线:0l x y m ++=都不是曲线()y f x =)的切线，则m 的取值范围是（）A ．(,1)(1,0)-∞--B ．(,1)(0,)-∞-+∞C ．(1,0)(0,)-+∞D ．a R ∈且0,1a a ≠≠-3. 【河北省保定市八校联合体2014届高三上学期第一次月考】已知函数()121210n n n n n f x x a x a x a x a ----=+++++()*2,n n N >∈,设0x 是函数()f x 的零点的最大值,则下述论断一定错误的是（）A.()0'0f x ≠B.()0'0f x =C.()0'0f x >D.()0'0f x <4. 【石家庄市2013届高中毕业班第一次模拟】已知定义域为R 的奇函数f(x)的导函数为'()f x ，当0x ≠时，'()()0f x f x x +>，若111(),2(2),ln (ln 2)222a fb fc f ==--=,则下列关于a,b,c 的大小关系正确的是（） A. a>b>c B. a>c>b C. c>b>aD. b>a>c5. 【山西省长治二中康杰中学临汾一中忻州一中2013届高三第四次四校联考】已知函数1)(+-=mx e x f x 的图像为曲线C ，若曲线C 存在与直线x y 21=垂直的切线，则实数m 的取值范围是( )A ．2≤mB ．2>mC ．21-≤m D ．21->m6. 【中原名校联盟2013——2014学年高三上期第一次摸底考试】已知函数f （x ）（x ∈R ）满足()f x '＞f （x ），则（）A ．f （2）＜2e f （0）B ．f （2）≤2e f （0）C ．f （2）＝2e f （0）D ．f （2）＞2e f （0）7. 【中原名校联盟2013——2014学年高三上期第一次摸底考试】曲线2y ＝x 与y ＝2x 围成的图形的面积为______________．8. 【2012-2013学年度南昌市高三第二次模拟测试卷】（本小题满分14分）已知函数x x x a x g 2)1ln(2)(2-++=（1）当0≠a 时，讨论函数)(x g 的单调性：（2）若函数)(x f 的图像上存在不同两点,A B ，设线段AB 的中点为),(00y x P ，使得)(x f 在点))(,(00x f x Q 处的切线l 与直线AB 平行或重合，则说函数)(x f 是“中值平衡函数”，切线l 叫做函数)(x f 的“中值平衡切线”。

高考数学各地名校试题解析分类汇编(一)3 导数1 文

各地解析分类汇编:导数（1）1 【山东省师大附中2013届高三上学期期中考试数学文】方程3269100x x x -+-=的实根个数是 A.3 B.2 C.1D.0【答案】C【解析】设32()6910f x x x x =-+-，2'()31293(1)(3)f x x x x x =-+=--，由此可知函数的极大值为(1)60f =-<，极小值为(3)100f =-<，所以方程3269100x x x -+-=的实根个数为1个.选C.2 【山东省实验中学2013届高三第二次诊断性测试数学文】曲线x x y +=331在点⎪⎭⎫ ⎝⎛341，处的切线与坐标轴围成的三角形面积为 A.92 B.91 C.31 D.32【答案】B【解析】2''()+1y f x x ==，在点⎪⎭⎫⎝⎛341，的切线斜率为'(1)2k f ==。

所以切线方程为42(1)3y x -=-，即223y x =-，与坐标轴的交点坐标为21(0,),(,0)33-，所以三角形的面积为11212339⨯⨯-=，选B.3 【山东省实验中学2013届高三第二次诊断性测试数学文】若)2ln(21)(2++-=x b x x f 在），（∞+-1上是减函数，则b 的取值范围是A.[]∞+-，1B.），（∞+-1C.]1-∞-，（D.），（1-∞- 【答案】C【解析】函数的导数'()2b f x x x =-++，要是函数在），（∞+-1上是减函数，则'()02b f x x x =-+≤+，在），（∞+-1恒成立，即2b x x ≤+，因为1x >-，所以210x +>>，即(2)b x x ≤+成立。

设(2)y x x =+，则222(1)1y x x x =+=+-，因为1x >-，所以1y >-，所以要使(2)b x x ≤+成立，则有1b ≤-，选C.4 【山东省聊城市东阿一中2013届高三上学期期初考试】若函数(1)4a xy ex -=+（x ∈R ）有大于零的极值点，则实数a 范围是（） A ．3a >- B ．3a <- C ．13a >- D ．13a <-【答案】B【解析】解：因为函数y=e （a-1）x+4x ，所以y ′=（a-1）e（a-1）x+4（a ＜1），所以函数的零点为x 0=14lna 1a 1--+，因为函数y=e （a-1）x +4x （x ∈R ）有大于零的极值点，故14lna 1a 1--+＝0，得到a<-3,选B5 【山东省临沂市2013届高三上学期期中考试数学文】已知32(),f x ax bx c =++其导函数()f x '的图象如右图，则函数()f x 的极小值是A ．a b c ++B ．84a b c ++C ．32a b +D ．c【答案】D【解析】由导函数()f x '的图象知当0x <时，()0f x '<，当02x <<时，()0f x '>，所以函数()f x 的极小值为(0)f c =，选D.6 【山东省青岛市2013届高三上学期期中考试数学（文）】已知1()c o s ,f x x x=则()()2f f ππ'+=A ．2π-B ．3πC ．1π-D ．3π-【答案】D【解析】因为1()cos ,f x x x=所以211'()cos sin f x x x xx=--，所以1()f ππ=-，2'()2f ππ=-，所以3()()2f f πππ'+=-，选D.7 【山东省济南外国语学校2013届高三上学期期中考试文科】若a>0,b>0,且函数224)(23---=bx axx x f 在x=1处有极值，则ab 的最大值（）A.2B.3C.6D.9 【答案】D【解析】函数的导数为2'()1222f x x a x b =--，函数在1x =处有极值，则有'(1)1222f a b =--=，即6a b +=，所以6a b =+≥，即9a b ≤，当且仅当3a b ==时取等号，选D.8 【山东省济南外国语学校2013届高三上学期期中考试文科】函数f(x)的定义域为R ，f(-1)=2,对任意x R ∈，2)(/>x f ,则()24f x x >+的解集为( )A.(-1，1)B.(-1，+∞)C.(-∞，-l)D.(-∞,+∞) 【答案】B【解析】设()()(24)F x f x x =-+,则(1)(1)(24)220F f -=---+=-=，'()'()2F x f x =-，对任意x R ∈，有'()'()20F x f x=->，即函数()F x 在R 上单调递增，则()0F x >的解集为(1,)-+∞，即()24f x x >+的解集为(1,)-+∞，选B.9 【山东省实验中学2013届高三第三次诊断性测试文】已知)1('2)(2xf x x f +=，则=)0('f .【答案】-4【解析】函数的导数为'()22'(1)f x x f =+，所以'(1)22'(1)f f =+，解得'(1)2f =-，所以2()4f x x x =-，所以'()24f x x =-，所以'(0)4f =-。

高考数学各地名校试题解析分类汇编(一)3 导数2 理

各地解析分类汇编:导数21【山东省烟台市2013届高三上学期期中考试理】（本小题满分13分）已知函数)(ln )(R a x ax x f ∈+=.（1）求)(x f 的极值；（2）若函数)(x f 的图象与函数1)(=x g 的图象在区间],0(2e 上有公共点，求实数a 的取值范围.【答案】（1）)(x f 的定义域为),0(+∞,2)(ln 1)('x a x x f +-=，……2分令0)('=x f 得a e x -=1，当),0(1ae x -∈时，,0)('>xf )(x f 是增函数；当),(1+∞∈-aex 时，,0)('<x f )(x f 是减函数，∴)(x f 在a e x -=1处取得极大值，11)()(--==a ae ef x f 极大值，无极小值.………………5分（2）①当21e e a <-时，即1->a 时，由（1）知)(x f 在),0(1ae-上是增函数，在],(21e e a -上是减函数，11max )()(--==∴a a e e f x f ,又当a e x -=时，0)(=x f ，当],0(aex -∈时，0)(<x f ；当],(2e e x a -∈时，0)(>x f ；Θ)(x f 与图象1)(=x g 的图象在],0(2e 上有公共点，11≥∴-a e ，解得1≥a ，又1->a ，所以1≥a . ………9分②当21e e a ≥-时，即1-≤a 时，)(x f 在],0(2e 上是增函数， ∴)(xf 在],0(2e 上的最大值为222)(eae f +=，所以原问题等价于122≥+ea，解得22-≥e a . 又1-≤a ,∴无解. 综上，实数a 的取值范围是),1[+∞. ……13分2.【山东省实验中学2013届高三第三次诊断性测试理】（本小题满分14分）已知函数)(x f 的导数b a b f ax x x f ,,)0(,33)('2=-=为实数，21<<a .（Ⅰ）若)(x f 在区间［-1，1］上的最小值、最大值分别为-2、1，求a 、b 的值；（Ⅱ）在（Ⅰ）的条件下，求经过点）（1,2P 且与曲线)(x f 相切的直线l 的方程；（Ⅲ）设函数xex x f x F 2]16)('[)(⋅++=，试判断函数)(x F 的极值点个数。

理科数学真题分类汇编专题3 导数的几何意义、定积分与微积分基本定理答案

x
2x
2
12．A【解析】点 (1,0) 处的切线斜率为 k ， k = y x =1 = 312 − 2 = 1 ，由点斜式可得切线
方程为 A．
13．D【解析】因为 y'
= −4e x (ex +1)2
= −4 ex +2 +ex
−1，即 tan
≥－1，所以 3 4
．
14． y = 2x 【解析】∵ y = 2ln(x +1) ，∴ y = 2 ．当 x = 0 时， y = 2， x +1
h(x) = 1− 1 x
=
x
−1 x
，所以
h(
x
)min
= h(1) = 0 ，故
x −1≥ln x，
可知曲线C ： y = ln x 在点P(1,0) 附近位于直线 l 的下侧，⑤错误．
25．2【解析】 y = x −1，则k = ，故切线方程 y = x过点(1, 2) 解得 = 2 ．
26．3【解析】 T x 2dx = x3 T = T 3 = 9 T = 3 ．
线的斜率4a − b = − 7 ②，由①②解得a = −1, b = −2 ，所以 a + b = −3． 42
24．①③④【解析】对于①，y = 3x2 , y |x=0 = 0 ，所以 l : y = 0是曲线C : y = x 3 在点 P(0,0)
处的切线，画图可知曲线C : y = x 3 在点 P(0,0) 附近位于直线 l 的两侧，①正确；对于
2(1 + x) ndx.
0
从而得到如下等式：
Cn0
1 2
+
1 2
Cn1

【2013备考】各地名校试题解析分类汇编(一)理科数学：3导数1

各地解析分类汇编:导数11【云南省玉溪一中2013届高三上学期期中考试理】已知曲线x x y ln 342-=的一条切线的斜率为21，则切点的横坐标为( ) A. 3 B. 2C. 1D.21 【答案】A【解析】函数的定义域为(0,)+∞，函数的导数为3'2x y x =-，由31'22x y x =-=，得260x x --=，解得3x =或1x =-（舍去），选A. 2【云南师大附中2013届高三高考适应性月考卷（三）理科】如图3，直线y=2x 与抛物线y=3－x 2所围成的阴影部分的面积是（）A ．353B ．C ．2D ．323【答案】D【解析】12332(32)d 3S x x x -=--=⎰，故选D. 3【云南省玉溪一中2013届高三第三次月考理】如图所示，曲线2x y =和曲线x y =围成一个叶形图（阴影部分），则该叶形图的面积是（）A.21 B. 41 C. 61 D. 31 【答案】D【解析】由2y xy ⎧=⎪⎨=⎪⎩11x y =⎧⎨=⎩或00x y =⎧⎨=⎩，所以根据积分的应用可得阴影部分的面积为3123120021211)()33333x dx x x =-=-=⎰，选D. 4【山东省烟台市莱州一中2013届高三10月月考（理）】由直线2,21==x x ，曲线x y 1=及x 轴所谓成图形的面积为A.415B.417C.2ln 21D. 2ln 2【答案】D【解析】根据积分的应用可知所求22112211ln ln 2ln2ln 22dx x x==-=⎰，选D. 5【云南师大附中2013届高三高考适应性月考卷（三）理科】已知()f x 为R 上的可导函数，且,x R ∀∈均有()f x f >′（x ），则有（）A ．20132013(2013)(0),(2013)(0)e f f f e f -<>B ．20132013(2013)(0),(2013)(0)e f f f e f -<<C ．20132013(2013)(0),(2013)(0)e f f f e f ->>D ．20132013(2013)(0),(2013)(0)e f f f e f -><【答案】A【解析】构造函数()()x f x g x e=，则2()()()()()()()x x x xf x e e f x f x f xg x e e ''''--==，6【山东省烟台市莱州一中2013届高三10月月考（理）】曲线x e y 21=在点()2,4e处的切线与坐标轴所围三角形的面积为A.2eB.24eC.22eD.229e 【答案】A【解析】121'2x y e =，所以在点()2,4e 的导数为142211'22y e e ⨯==，即切线斜率为212k e =，所以切线方程为221(4)2y e e x -=-，令0x =得，2y e =-，令0y =，得2x =.所以三角形的面积为22122e e ⨯⨯=，选A. 7【云南省昆明一中2013届高三新课程第一次摸底测试理】函数22ln y x x e ==在处的切线与坐标轴所围成的三角形的面积为A ．292e B ．212Se =C ．22eD ．2e【答案】D 【解析】212'2y x x x=⨯=，所以在2x e=处的切线效率为22k e =，所以切线方程为2224()y x e e-=-，令0x =，得2y =，令0y =，得2x e =-，所以所求三角形的面积为22122e e ⨯⨯=，选D. 8【山东省烟台市莱州一中20l3届高三第二次质量检测（理）】曲线()ln 2y x =+在点()1,0P -处的切线方程是 A.1y x =+ B.1y x =-+C.21y x =+D.21y x =-+【答案】A 【解析】1'2y x =+,所以在点P 处的切线斜率1112k ==-+，所以切线方程为(1)1y x x =--=+，选A.9【山东省烟台市莱州一中20l3届高三第二次质量检测（理）】由直线2,,0sin 33x x y y x ππ====与所围成的封闭图形的面积为A.12B.1C.2【答案】B 【解析】由积分的应用得所求面积为2233332sin cos coscos 2cos 1333xdx xπππππππ=-=-+==⎰，选B. 10【天津市新华中学2012届高三上学期第二次月考理】已知函数))((R x x f ∈满足1)1(=f ，且)(x f 的导函数21)('<x f ，则212)(+<x x f 的解集为 A. {}11<<-x x B. {}1-<x x C. {}11>-<x x x 或 D. {}1>x x 【答案】D【解析】设1()()()22xF x f x =-+, 则11(1)(1)()11022F f =-+=-=，1'()'()2F x f x =-，对任意x R ∈，有1'()'()02F x f x =-<，即函数()F x 在R 上单调递减，则()0F x <的解集为(1,)+∞，即212)(+<x x f 的解集为(1,)+∞，选D.11【山东省烟台市莱州一中20l3届高三第二次质量检测（理）】函数()32f x x bx cx d=+++的大致图象如图所示，则2212x x +等于A.89B.109C.169D.289【答案】C【解析】函数过原点，所以0d =。

2021年高考真题理科数学解析汇编导数与积分

2021年高考真题理科数学解析汇编：导数与积分一、选择题1 ．〔2021年高考〔新课标理〕〕函数1()ln(1)f x x x=+-;那么()y f x =的图像大致为2 ．〔2021年高考〔浙江理〕〕设a >0,b >0.〔〕A ．假设2223a b a b +=+,那么a >bB ．假设2223a b a b +=+,那么a <bC ．假设2223a b a b -=-,那么a >bD ．假设2223a b a b -=-,那么a <b3 ．〔2021年高考〔重庆理〕〕设函数()f x 在R 上可导,其导函数为()f x ',且函数(1)()y x f x '=-的图像如题(8)图所示,那么以下结论中一定成立的是〔〕A ．函数()f x 有极大值(2)f 和极小值(1)fB ．函数()f x 有极大值(2)f -和极小值(1)fC ．函数()f x 有极大值(2)f 和极小值(2)f -D ．函数()f x 有极大值(2)f -和极小值(2)f4 ．〔2021年高考〔陕西理〕〕设函数()xf x xe =,那么〔〕A ．1x =为()f x 的极大值点B ．1x =为()f x 的极小值点C ．1x =-为()f x 的极大值点D ．1x =-为()f x 的极小值点5 ．〔2021年高考〔山东理〕〕设0a >且1a ≠,那么“函数()xf x a =在R 上是减函数〞,是“函数3()(2)g x a x =-在R 上是增函数〞的〔〕A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件6 ．〔2021年高考〔湖北理〕〕二次函数()y f x =的图象如下图,那么它与x 轴所围图形的面积为〔〕A ．2π5 B ．43C ．32D ．π27 ．〔2021年高考〔福建理〕〕如下图,在边长为1的正方形OABC 中任取一点P,1-y xO第3题图11那么点P 恰好取自阴影局部的概率为〔〕A ．14B ．15C ．16D ．178 ．〔2021年高考〔大纲理〕〕函数33y x x c =-+的图像与x 轴恰有两个公共点,那么c =〔〕A ．2-或2B ．9-或3C ．1-或1D ．3-或1二、填空题9 ．〔2021年高考〔上海理〕〕函数)(x f y =的图像是折线段ABC ,假设中A (0,0),B (21,5),C (1,0).函数)10()(≤≤=x x xf y 的图像与x 轴围成的图形的面积为_______ .10．〔2021年高考〔山东理〕〕设0a >.假设曲线y x =与直线,0x a y ==所围成封闭图形的面积为2a ,那么a =______.11．〔2021年高考〔江西理〕〕计算定积分121(sin )x x dx -+=⎰___________.12．〔2021年高考〔广东理〕〕曲线33y x x =-+在点()1,3处的切线方程为___________________. 三、解答题13．〔2021年高考〔天津理〕〕函数()=ln (+)f x x x a -的最小值为0,其中>0a .(Ⅰ)求a 的值;(Ⅱ)假设对任意的[0,+)x ∈∞,有2()f x kx ≤成立,求实数k 的最小值; (Ⅲ)证明=12ln (2+1)<221ni n i --∑*()n N ∈. 14．〔2021年高考〔新课标理〕〕函数()f x 满足满足121()(1)(0)2x f x f e f x x -'=-+;(1)求()f x 的解析式及单调区间; (2)假设21()2f x x ax b ≥++,求(1)a b +的最大值. 15．〔2021年高考〔浙江理〕〕a >0,b ∈R,函数()342f x ax bx a b =--+.(Ⅰ)证明:当0≤x ≤1时,(ⅰ)函数()f x 的最大值为|2a -b |﹢a ;(ⅱ) ()f x +|2a -b |﹢a ≥0;(Ⅱ) 假设﹣1≤()f x ≤1对x ∈[0,1]恒成立,求a +b 的取值范围.16．〔2021年高考〔重庆理〕〕(本小题总分值13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)设13()ln 1,22f x a x x x =+++其中a R ∈,曲线()y f x =在点(1,(1))f 处的切线垂直于y 轴.(Ⅰ) 求a 的值;(Ⅱ) 求函数()f x 的极值.17．〔2021年高考〔陕西理〕〕设函数()(,,)nn f x x bx cn N b c R +=++∈∈(1)设2n ≥,1,1b c ==-,证明:()n f x 在区间1,12⎛⎫⎪⎝⎭内存在唯一的零点;(2)设2n =,假设对任意12,x x [1,1]∈-,有2122|()()|4f x f x -≤,求b 的取值范围; (3)在(1)的条件下,设n x 是()n f x 在1,12⎛⎫⎪⎝⎭内的零点,判断数列23,,,nx x x 的增减性.18．〔2021年高考〔山东理〕〕函数ln ()xx kf x e+=(k 为常数, 2.71828e =⋅⋅⋅是自然对数的底数),曲线()y f x =在点(1,(1))f 处的切线与x 轴平行. (Ⅰ)求k 的值;(Ⅱ)求()f x 的单调区间;(Ⅲ)设2()()'()g x x x f x =+,其中'()f x 为()f x 的导函数.证明:对任意20,()1x g x e -><+.19．〔2021年高考〔辽宁理〕〕设()ln(1)(,,,)f x x ax b a b R a b =+++∈为常数,曲线()y f x =与直线32y x =在(0,0)点相切. (Ⅰ)求,a b 的值.(Ⅱ)证明:当02x <<时,9()6xf x x <+. 20．〔2021年高考〔江苏〕〕假设函数)(x f y =在0x x =处取得极大值或极小值,那么称0x 为函数)(x f y =的极值点.a b ，是实数,1和1-是函数32()f x x ax bx =++的两个极值点.(1)求a 和b 的值;(2)设函数()g x 的导函数()()2g x f x '=+,求()g x 的极值点;(3)设()(())h x f f x c =-,其中[22]c ∈-，,求函数()y h x =的零点个数.21．〔2021年高考〔湖南理〕〕函数()f x =axex =-,其中a ≠0.(1) 假设对一切x∈R,()f x ≥1恒成立,求a 的取值集合.(2)在函数()f x 的图像上取定两点11(,())A x f x ,22(,())B x f x 12()x x <,记直线AB 的斜率为K,问:是否存在x 0∈(x 1,x 2),使0()f x k '>成立?假设存在,求0x 的取值范围;假设不存在,请说明理由.22．〔2021年高考〔湖北理〕〕(Ⅰ)函数()(1)(0)r f x rx x r x =-+->,其中r 为有理数,且01r <<.求()f x 的最小值;(Ⅱ)试用(Ⅰ)的结果证明如下命题:设120,0a a ≥≥,12,b b 为正有理数. 假设121b b +=,那么12121122b b a a a b a b ≤+; (Ⅲ)请将(Ⅱ)中的命题推广到一般形式,并用数学归纳法．．．．．证明你所推广的命题. 注:当α为正有理数时,有求导公式1()x x ααα-'=.23．〔2021年高考〔广东理〕〕(不等式、导数)设1a <,集合{}0A x R x =∈>,(){}223160B x R x a x a =∈-++>,D A B =.(Ⅰ)求集合D (用区间表示);(Ⅱ)求函数()()322316f x x a x ax =-++在D 内的极值点.24．〔2021年高考〔福建理〕〕函数2()()xf x e ax ex a R =+-∈.(Ⅰ)假设曲线()y f x =在点(1,(1))f 处的切线平行于x 轴,求函数()f x 的单调区间; (Ⅱ)试确定a 的取值范围,使得曲线()y f x =上存在唯一的点P ,曲线在该点处的切线与曲线只有一个公共点P .25．〔2021年高考〔大纲理〕〕(注意:在试题卷上作答无效．．．．．．．．．)设函数()cos ,[0,]f x ax x x π=+∈. (1)讨论()f x 的单调性;(2)设()1sin f x x ≤+,求a 的取值范围.26．〔2021年高考〔北京理〕〕函数2()1f x ax =+(0a >),3()g x x bx =+.(1)假设曲线()y f x =与曲线()y g x =在它们的交点(1,c )处具有公共切线,求,a b 的值;(2)当24a b =时,求函数()()f x g x +的单调区间,并求其在区间(,1]-∞-上的最大值.27．〔2021年高考〔安徽理〕〕(本小题总分值13分)设1()(0)x xf x ae b a ae =++> (I)求()f x 在[0,)+∞上的最小值;(II)设曲线()y f x =在点(2,(2))f 的切线方程为32y x =;求,a b 的值.2021年高考真题理科数学解析汇编：导数参考答案一、选择题1. 【解析】选B得:0x >或10x -<<均有()0f x < 排除,,A C D2. 【答案】A【解析】假设2223a b a b +=+,必有2222a b a b +>+.构造函数:()22x f x x =+,那么()2ln 220x f x '=⋅+>恒成立,故有函数()22x f x x =+在x >0上单调递增,即a >b 成立.其余选项用同样方法排除. 3. 【答案】D【解析】2,10x x <-->,由(1)()0()0x f x f x ''->⇒>,函数()f x 为增;21,10x x -<<->,由(1)()0()0x f x f x ''-<⇒<,函数()f x 为减; 12,10x x <<-<,由(1)()0()0x f x f x ''->⇒<,函数()f x 为减; 2,10x x >-<,由(1)()0()0x f x f x ''-<⇒>,函数()f x 为增.【考点定位】判断函数的单调性一般利用导函数的符号,当导函数大于0,那么函数为增,当导函数小于0那么函数递减.4. 解析:()(1)xf x x e '=+,令()0,f x '=得1x =-,1x时,()0f x '<,()x f x xe =为减函数;1x时,()0f x '>,()x f x xe =为增函数,所以1x =-为()f x 的极小值点,选D.5. 【解析】假设函数xa x f =)(在R 上为减函数,那么有10<<a .函数3)2()(x a x g -=为增函数,那么有02>-a ,所以2<a ,所以“函数xa x f =)(在R 上为减函数〞是“函数3)2()(x a x g -=为增函数〞的充分不必要条件,选A.6. 考点分析:此题考察利用定积分求面积.解析:根据图像可得: 2()1y f x x ==-+,再由定积分的几何意义,可求得面积为12311114(1)()33S x dx x x --=-+=-+=⎰. 7. 【答案】C【解析】312201211)()13260S x dx x x S ==-==⎰正阴影,故16P =,答案C 【考点定位】此题主要考查几何概型的概率和定积分,考查推理能力、计算求解能力.8. 答案A【命题意图】本试题主要考查了导数在研究三次函数中的极值的运用.要是函数图像与x轴有两个不同的交点,那么需要满足极佳中一个为零即可. 【解析】因为三次函数的图像与x 轴恰有两个公共点,结合该函数的图像,可得极大值或者极小值为零即可满足要求.而2()333()(1)f x x x x '=-=-+,当1x =±时取得极值由(1)0f =或(1)0f -=可得20c -=或20c +=,即2c =±.二、填空题 9. [解析]如图1,⎩⎨⎧≤<-≤≤=1,10100,10)(2121x x x x x f所以⎩⎨⎧≤<+-≤≤==1,10100,10)(212212x x x x x x xf y 易知,y =xf (x )的分段解析式中的两局部抛物线形状完全相同,只是开口方向及顶点位置不同,如图2,封闭图形MNO 与OMP 全等,面积相等,故所求面积即为矩形ODMP 的面积S=452521=⨯.[评注]对于曲边图形,上海现行教材中不出微积分,能用微积分求此面积的考生恐是极少的,而对于极大局部考生,等积变换是唯一的出路.10. 【解析】由得223023032|32a a x x S a a====⎰,所以3221=a ,所以94=a .11.23【解析】此题考查有关多项式函数,三角函数定积分的应用. 31211111112(sin )cos |cos1cos1333333x x x dx x --⎛⎫-⎛⎫⎛⎫+=-=---=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰. 【点评】这里,许多学生容易把原函数写成3cos 3x x +,主要是把三角函数的导数公式记混而引起的.表达考纲中要求了解定积分的概念.来年需要注意定积分的几何意义求曲面面积等.12.解析:210x y -+=.21|3112x y ='=⨯-=,所以切线方程为()321y x -=-,即210x y -+=.三、解答题13. 【命题意图】本试题主要考查导数的运算、利用导数研究函数的单调性、不等式等根底知识,考查函数思想、分类讨论思想、考查综合分析和解决问题的能力. (1)()f x 的定义域为(,)a -+∞得：1x a =-时，min ()(1)101f x f a a a =-⇔-=⇔= 〔2〕设22()()ln(1)(0)g x kx f x kx x x x =-=-++≥那么()0g x ≥在[0,+)x ∈∞上恒成立min ()0(0)g x g ⇔≥=〔*〕 ①当1210()2k k -<<时，0012()00()(0)02k g x x x g x g k-'≤⇔≤≤=⇒<=与〔*〕矛盾②当12k ≥时，min ()0()(0)0g x g x g '≥⇒==符合〔*〕得：实数k 的最小值为12(lfxlby)〔3〕由〔2〕得：21ln(1)2x x x -+<对任意的0x >值恒成立取2(1,2,3,,)21x i n i ==-：222[ln(21)ln(21)]21(21)i i i i -+--<-- 当1n =时，2ln32-< 得：=12ln (2+1)<221ni n i --∑〔lb ylfx 〕当2i ≥时，2211(21)2321i i i <----得：121[ln(21)ln(21)]2ln 3122121ni i i i n =-++-<-+-<--∑【点评】试题分为三问,题面比拟简单,给出的函数比拟常规,因此入手对于同学们来说没有难度,第二问中,解含参数的不等式时,要注意题中参数的讨论所有的限制条件,从而做到不重不漏;第三问中,证明不等式,应借助于导数证不等式的方法进行.14. 【解析】(1)1211()(1)(0)()(1)(0)2x x f x f e f x x f x f e f x --'''=-+⇒=-+令1x =得:(0)1f = 得:21()()()12xx f x e x x g x f x e x '=-+⇒==-+ ()10()x g x e y g x '=+>⇒=在x R ∈上单调递增得:()f x 的解析式为21()2xf x e x x =-+且单调递增区间为(0,)+∞,单调递减区间为(,0)-∞ (2)21()()(1)02x f x x ax b h x e a x b ≥++⇔=-+-≥得()(1)x h x e a '=-+ ①当10a +≤时,()0()h x y h x '>⇒=在x R ∈上单调递增x →-∞时,()h x →-∞与()0h x ≥矛盾②当10a +>时,()0ln(1),()0ln(1)h x x a h x x a ''>⇔>+<⇔<+ 得:当ln(1)x a =+时,min ()(1)(1)ln(1)0h x a a a b =+-++-≥ 令22()ln (0)F x x x x x =->;那么()(12ln )F x x x '=-当x =,max ()2e F x =当1,a b ==,(1)a b +的最大值为2e 15. 【解析】此题主要考察不等式,导数,单调性,线性规划等知识点及综合运用能力.(Ⅰ)(ⅰ)()2122f x ax b '=-.当b ≤0时,()2122f x ax b '=->0在0≤x ≤1上恒成立,此时()f x 的最大值为:()1423f a b a b a b =--+=-=|2a -b |﹢a ; 当b >0时,()2122f x ax b '=-在0≤x ≤1上的正负性不能判断, 此时()f x 的最大值为:()max 2max{(0)1}max{()3}32b a b af x f f b a a b a b b a ->⎧==--=⎨-<⎩，，（），()，=|2a -b |﹢a ; 综上所述:函数()f x 在0≤x ≤1上的最大值为|2a -b |﹢a ; (ⅱ) 要证()f x +|2a -b |﹢a ≥0,即证()g x =﹣()f x ≤|2a -b |﹢a . 亦即证()g x 在0≤x ≤1上的最大值小于(或等于)|2a -b |﹢a ,∵()342g x ax bx a b =-++-,∴令()21220g x ax b x '=-+=⇒=. 当b ≤0时,()2122g x ax b '=-+<0在0≤x ≤1上恒成立, 此时()g x 的最大值为:()03g a b a b =-<-=|2a -b |﹢a ; 当b <0时,()2122g x ax b '=-+在0≤x ≤1上的正负性不能判断, ≤|2a -b |﹢a ;综上所述:函数()g x 在0≤x ≤1上的最大值小于(或等于)|2a -b |﹢a . 即()f x +|2a -b |﹢a ≥0在0≤x ≤1上恒成立.(Ⅱ)由(Ⅰ)知:函数()f x 在0≤x ≤1上的最大值为|2a -b |﹢a ,且函数()f x 在0≤x ≤1上的最小值比﹣(|2a -b |﹢a )要大. ∵﹣1≤()f x ≤1对x ∈[0,1]恒成立, ∴|2a -b |﹢a ≤1.取b 为纵轴,a 为横轴. 那么可行域为:21b a b a ≥⎧⎨-≤⎩和231b aa b <⎧⎨-≤⎩,目标函数为z =a +b .作图如下:由图易得:当目标函数为z =a +b 过P (1,2)时,有max 3z =,min 1z =-.∴所求a +b 的取值范围为:[]13-，. 【答案】(Ⅰ) 见解析;(Ⅱ) []13-，. 16. 【考点定位】本小题主要考查利用导数研究曲线上某点切线方程、函数的最值及其几何意义,两条直线平行的判定等根底知识,考查运算求解能力. 解:(1)因()13ln 122f x a x x x =+++,故()21322a f x x x '=-+ 由于曲线()y f x =在点()()1,1f 处的切线垂直于y 轴,故该切线斜率为0,即()10f '=,从而13022a -+=,解得1a =- (2)由(1)知()()13ln 1022f x x x x x =-+++>,令()0f x '=,解得1211,3x x ==-(因213x =-不在定义域内,舍去),当()0,1x ∈时,()0f x '<,故()f x 在()0,1上为减函数; 当()1,x ∈+∞时,()0f x '>,故()f x 在()1,+∞上为增函数; 故()f x 在1x =处取得极小值()13f =.17.解析:(1)1,1b c ==-,2n ≥时,()1nn f x x x =+-∵111()(1)()10222n n nf f =-⨯<,∴()n f x 在1,12⎛⎫⎪⎝⎭内存在零点. 又当1,12x ⎛⎫∈ ⎪⎝⎭时,1()10n n f x nx -'=+>∴ ()n f x 在1,12⎛⎫⎪⎝⎭上是单调递增的,所以()n f x 在1,12⎛⎫⎪⎝⎭内存在唯一零点. (2)当2n =时,22()f x x bx c =++对任意12,[1,1]x x ∈-都有2122|()()|4f x f x -≤等价于2()f x 在[1,1]-上最大值与最小值之差4M ≤,据此分类讨论如下:(ⅰ)当||12b>,即||2b >时, 22|(1)(1)|2||4M f f b =--=>,与题设矛盾(ⅱ)当102b-≤-<,即02b <≤时, 222(1)()(1)422b bM f f =---=+≤恒成立(ⅲ)当012b≤≤,即20b -≤≤时,222(1)()(1)422b bM f f =---=-≤恒成立.综上可知,22b -≤≤注:(ⅱ)(ⅲ)也可合并证明如下: 用max{,}a b 表示,a b 中的较大者.当112b-≤≤,即22b -≤≤时, 2||(1)42b =+≤恒成立 (3)证法一设n x 是()n f x 在1,12⎛⎫⎪⎝⎭内的唯一零点(2)n ≥ ()1n n n n n f x x x =+-,11111()10n n n n n f x x x +++++=+-=,11,12n x +⎛⎫∈ ⎪⎝⎭于是有11111111()0()11()n nn n n n n n n n n n f x f x x x x x f x ++++++++===+-<+-=又由(1)知()n f x 在1,12⎛⎫⎪⎝⎭上是递增的,故1(2)n n x x n +<≥, 所以,数列23,,,nx x x 是递增数列.证法二设n x 是()n f x 在1,12⎛⎫⎪⎝⎭内的唯一零点那么1()n f x +的零点1n x +在(,1)n x 内,故1(2)n n x x n +<≥, 所以,数列23,,,nx x x 是递增数列.18.解析:由f(x) = x e k x +ln 可得=')(x f xexk x ln 1--,而0)1(='f ,即01=-e k ,解得1=k ;(Ⅱ)=')(x f xexx ln 11--,令0)(='x f 可得1=x , 当10<<x 时,0ln 11)(>--='x x x f ;当1>x 时,0ln 11)(<--='x xx f .于是)(x f 在区间)1,0(内为增函数;在),1(+∞内为减函数.(Ⅲ)xx ex x x x e xx x x x g ln )(1ln 11)()(222+--=--+=, (1)当1≥x 时, 0,0,0ln ,0122>>+≥≤-xe x x x x ,210)(-+<≤ex g .(2)当10<<x 时,要证221ln 11)()(-+<--+=e exx x x x g x. 只需证)ln 1(1112x x e ex x +-+<+-即可设函数)1,0(),ln 1(1)(,1)(∈+-=+=x x x x q e x x p e . 那么)1,0(,ln 2)(,0)(∈--='<-='x x x q exx p x ,那么当10<<x 时1)0(1)(=<+=p ex x p e ,令0ln 2)(=--='x x q 解得)1,0(2∈=-ex ,当),0(2-∈e x 时0)(>'x q ;当)1,(2-∈e x 时0)(<'x q ,那么当10<<x 时221)()ln 1(1)(--+=≤+-=e e q x x x q ,且0)(>x q ,那么≥+-+-)ln 1(112x x e 11122=++--e e ,于是可知当10<<x 时)ln 1(1112x x e ex x +-+<+-成立综合(1)(2)可知对任意x>0,21)(-+<e x g 恒成立.另证1:设函数)1,0(,1)(∈+=x e x x p e ,那么0)(<-='xe xx p , 那么当10<<x 时1)0(1)(=<+=p ex x p x ,于是当10<<x 时,要证221)ln 11(ln 11)()(-+<--<--+=e x x x exx x x x g x, 只需证21)ln 11(-+<--e x xx 即可,设)1,0(),ln 1(1)(∈+-=x x x x q ,)ln 1(1)(x x x q +-=', 令0ln 2)(=--='x x q 解得)1,0(2∈=-ex ,当),0(2-∈e x 时0)(>'x q ;当)1,(2-∈e x 时0)(<'x q , 那么当10<<x 时221)()ln 1(1)(--+=≤+-=e e q x x x q ,于是可知当10<<x 时221ln 11)(-+<--+e exx x x x成立综合(1)(2)可知对任意x>0,21)(-+<e x g 恒成立.另证2:根据重要不等式当10<<x 时x x <+)1ln(,即xe x <+1,于是不等式221)ln 11(ln 11)()(-+<--<--+=e x x x exx x x x g x, 设)1,0(),ln 1(1)(∈+-=x x x x q ,)ln 1(1)(x x x q +-=', 令0ln 2)(=--='x x q 解得)1,0(2∈=-ex ,当),0(2-∈e x 时0)(>'x q ;当)1,(2-∈e x 时0)(<'x q , 那么当10<<x 时221)()ln 1(1)(--+=≤+-=e e q x x x q ,于是可知当10<<x 时221ln 11)(-+<--+e exx x x x成立. 19. 【答案及解析】【点评】此题综合考查导数的概念、几何意义、导数在判断函数单调性与最值中的运用.此题容易忽略函数)(x f 的定义域,根据条件曲线()y f x =与直线32y x =在(0,0)点相切,求出,a b 的值,然后,利用函数的单调性或者均值不等式证明9()6xf x x <+即可.从近几年的高考命题趋势看,此类型题目几乎年年都有涉及,因此,在平时要加强训练.此题属于中档题.20. 【答案】解:(1)由32()f x x ax bx =++,得2()32f'x x ax b =++.∵1和1-是函数32()f x x ax bx =++的两个极值点,∴ (1)32=0f'a b =++,(1)32=0f'a b -=-+,解得==3a b -0，. (2)∵ 由(1)得,3()3f x x x =- ,∴()()23()()2=32=12g x f x x x x x '=+-+-+,解得123==1=2x x x -，. ∵当2x <-时,()0g x <';当21<x <-时,()0g x >', ∴=2x -是()g x 的极值点.∵当21<x <-或1x >时,()0g x >',∴ =1x 不是()g x 的极值点. ∴()g x 的极值点是-2.(3)令()=f x t ,那么()()h x f t c =-.先讨论关于x 的方程()=f x d 根的情况:[]2, 2d ∈-当=2d 时,由(2 )可知,()=2f x -的两个不同的根为I 和一 2 ,注意到()f x 是奇函数,∴()=2f x 的两个不同的根为一和2.当2d <时,∵(1)=(2)=20f d f d d >----,(1)=(2)=20f d f d d <----- , ∴一2 , -1,1 ,2 都不是()=f x d 的根. 由(1)知()()()=311f'x x x +-.① 当()2x ∈+∞，时,()0f'x > ,于是()f x 是单调增函数,从而()(2)=2f x >f . 此时()=f x d 在()2+∞，无实根. ② 当()1 2x ∈，时.()0f'x >,于是()f x 是单调增函数. 又∵(1)0f d <-,(2)0f d >-,=()y f x d -的图象不间断,∴()=f x d 在(1 , 2 )内有唯一实根.同理,()=f x d 在(一2 ,一I )内有唯一实根.③ 当()11x ∈-，时,()0f'x <,于是()f x 是单调减两数. 又∵(1)0f d >--, (1)0f d <-,=()y f x d -的图象不间断,∴()=f x d 在(一1,1 )内有唯一实根.因此,当=2d 时,()=f x d 有两个不同的根12x x ，满足12=1 =2x x ，;当2d < 时 ()=f x d 有三个不同的根315x x x ，，,满足2 =3, 4, 5i x <i ，. 现考虑函数()y h x =的零点:( i )当=2c 时,()=f t c 有两个根12t t ，,满足12==2t t 1，. 而1()=f x t 有三个不同的根,2()=f x t 有两个不同的根,故()y h x =有5 个零点.( 11 )当2c <时,()=f t c 有三个不同的根345t t t ，，,满足2 =3, 4, 5i t <i ，. 而() =3,() 4, = 5i f x t i 有三个不同的根,故()y h x =有9 个零点.综上所述,当=2c 时,函数()y h x =有5 个零点;当2c <时,函数()y h x =有9 个零点. 【考点】函数的概念和性质,导数的应用.【解析】(1)求出)(x f y =的导数,根据1和1-是函数)(x f y =的两个极值点代入列方程组求解即可.(2)由(1)得,3()3f x x x =-,求出()g x ',令()=0g x ',求解讨论即可.(3)比拟复杂,先分=2d 和2d <讨论关于x 的方程()=f x d 根的情况;再考虑函数()y h x =的零点.21. 【解析】(Ⅰ)假设0a <,那么对一切0x >,()f x 1axex =-<,这与题设矛盾,又0a ≠,故0a >.而()1,axf x ae '=-令11()0,ln .f x x a a'==得当11ln x a a <时,()0,()f x f x '<单调递减;当11ln x a a >时,()0,()f x f x '>单调递增,故当11ln x a a =时,()f x 取最小值11111(ln )ln .f a a a a a=-于是对一切,()1x R f x ∈≥恒成立,当且仅当111ln 1a a a-≥. ① 令()ln ,g t t t t =-那么()ln .g t t '=-当01t <<时,()0,()g t g t '>单调递增;当1t >时,()0,()g t g t '<单调递减. 故当1t =时,()g t 取最大值(1)1g =.因此,当且仅当11a=即1a =时,①式成立. 综上所述,a 的取值集合为{}1.(Ⅱ)由题意知,21212121()() 1.ax ax f x f x e e k x x x x --==---令2121()(),ax ax axe e xf x k ae x x ϕ-'=-=--那么令()1t F t e t =--,那么()1tF t e '=-.当0t <时,()0,()F t F t '<单调递减;当0t >时,()0,()F t F t '>单调递增. 故当0t =,()(0)0,F t F >=即10.te t -->从而21()21()10a x x ea x x ---->,12()12()10,a x x ea x x ---->又1210,ax e x x >-2210,ax e x x >-所以1()0,x ϕ<2()0.x ϕ>因为函数()y x ϕ=在区间[]12,x x 上的图像是连续不断的一条曲线,所以存在012(,)x x x ∈使0()0,x ϕ=2()0,()ax x a e x ϕϕ'=>单调递增,故这样的c 是唯一的,且21211ln ()ax ax e e c a a x x -=-.故当且仅当212211(ln ,)()ax ax e e x x a a x x -∈-时, 0()f x k '>.综上所述,存在012(,)x x x ∈使0()f x k '>成立.且0x 的取值范围为212211(ln ,)()ax ax e e x a a x x --. 【点评】此题考查利用导函数研究函数单调性、最值、不等式恒成立问题等,考查运算能力,考查分类讨论思想、函数与方程思想,转化与划归思想等数学思想方法.第一问利用导函数法求出()f x 取最小值11111(ln )ln .f a a a a a=-对一切x∈R,f(x) ≥1恒成立转化为min ()1f x ≥,从而得出a 的取值集合;第二问在假设存在的情况下进行推理,通过构造函数,研究这个函数的单调性及最值来进行分析判断.22.考点分析:此题主要考察利用导数求函数的最值,并结合推理,考察数学归纳法,对考生的归纳推理能力有较高要求.解析:(Ⅰ)11()(1)r r f x r rx r x --'=-=-,令()0f x '=,解得1x =.当01x <<时,()0f x '<,所以()f x 在(0,1)内是减函数; 当 1x > 时,()0f x '>,所以()f x 在(1,)+∞内是增函数.故函数()f x 在1x =处取得最小值(1)0f =. (Ⅱ)由(Ⅰ)知,当(0,)x ∈+∞时,有()(1)0f x f ≥=,即(1)r x rx r ≤+- ① 假设1a ,2a 中有一个为0,那么12121122b b a a a b a b ≤+成立; 假设1a ,2a 均不为0,又121b b +=,可得211b b =-,于是在①中令12a x a =,1r b =,可得1111122()(1)b a ab b a a ≤⋅+-, 即111121121(1)b b a a a b a b -≤+-,亦即12121122b b a a a b a b ≤+.综上,对120,0a a ≥≥,1b ,2b 为正有理数且121b b +=,总有12121122b b a a a b a b ≤+. ② (Ⅲ)(Ⅱ)中命题的推广形式为:设12,,,n a a a 为非负实数,12,,,n b b b 为正有理数.假设121n b b b +++=,那么12121122n b b b n n n a a a a b a b a b ≤+++. ③用数学归纳法证明如下:(1)当1n =时,11b =,有11a a ≤,③成立. (2)假设当n k =时,③成立,即假设12,,,k a a a 为非负实数,12,,,k b b b 为正有理数,且121k b b b +++=,那么12121122k b b b k k k a a a a b a b a b ≤+++.当1n k =+时,121,,,,k k a a a a +为非负实数,121,,,,k k b b b b +为正有理数,且1211k k b b b b +++++=,此时101k b +<<,即110k b +->,于是111212121121()k k k k b b b b b b b b kk k k a aa aa aa a++++==12111111111121()kk k k k k b b b b b b b b kk aaaa +++++----+.因121111111kk k k b b b b b b ++++++=---,由归纳假设可得1211111112k k k k b b b b b b kaaa+++---≤1212111111k k k k k b b b a a a b b b +++⋅+⋅++⋅---112211k kk a b a b a b b ++++=-, 从而112121k k b b b b k k a a a a ++≤1111122111k k b b k k k k a b a b a b a b ++-++⎛⎫+++ ⎪-⎝⎭.又因11(1)1k k b b ++-+=,由②得 112211k k k k a b a b a b a b ++=++++,从而112121k k b b b b k k a a a a ++112211k k k k a b a b a b a b ++≤++++.故当1n k =+时,③成立.由(1)(2)可知,对一切正整数n ,所推广的命题成立.说明:(Ⅲ)中如果推广形式中指出③式对2n ≥成立,那么后续证明中不需讨论1n =的情况.23.解析:(Ⅰ)考虑不等式()223160x a x a -++>的解.因为()()()2314263331a a a a ∆=⎡-+⎤-⨯⨯=--⎣⎦,且1a <,所以可分以下三种情况: ①当113a <<时,0∆<,此时B =R ,()0,D A ==+∞. ②当13a =时,0∆=,此时{}1B x x =≠,()()0,11,D =+∞.③当13a <时,0∆>,此时()223160x a x a -++=有两根,设为1x 、2x ,且12x x <,那么1x =2x =,于是{}12B x x x x x =<>或.当103a <<时,()123102x x a +=+>,1230x x a =>,所以210x x >>,此时()()120,,D x x =+∞;当0a ≤时,1230x x a =≤,所以10x ≤,20x >,此时()2,D x =+∞.综上所述,当113a <<时,()0,D A ==+∞;当13a =时,()()0,11,D =+∞;当103a <<时,()()120,,D x x =+∞;当0a ≤时,()2,D x =+∞.其中1x =2x =.(Ⅱ)()()26616f x x a x a '=-++,令()0f x '=可得()()10x a x --=.因为1a <,所以()0f x '=有两根1m a =和21m =,且12m m <.①当113a <<时,()0,D A ==+∞,此时()0f x '=在D 内有两根1m a =和21m =,列表可得x()0,aa(),1a1 ()1,+∞()f x ' + 0 - 0 + ()f x递增极小值递减极大值递增所以()f x 在D 内有极大值点1,极小值点a . ②当13a =时,()()0,11,D =+∞,此时()0f x '=在D 内只有一根113m a ==,列表可得 x10,3⎛⎫ ⎪⎝⎭131,13⎛⎫ ⎪⎝⎭()1,+∞()f x ' + 0 - + ()f x递增极小值递减递增所以()f x 在D 内只有极小值点a ,没有极大值点.③当103a <<时,()()120,,D x x =+∞,此时1201a x x <<<<(可用分析法证明),于是()0f x '=在D 内只有一根1m a =,列表可得x()0,aa()1,a x()2,x +∞()f x ' + 0 - + ()f x递增极小值递减递增所以()f x 在D 内只有极小值点a ,没有极大值点.④当0a ≤时,()2,D x =+∞,此时21x >,于是()f x '在D 内恒大于0,()f x 在D 内没有极值点.综上所述,当113a <<时,()f x 在D 内有极大值点1,极小值点a ;当103a <≤时,()f x 在D 内只有极小值点a ,没有极大值点.当0a ≤时,()f x 在D 内没有极值点.24. 【考点定位】此题主要考查函数的导数、导数的应用、二次函数的性质、函数的零点等根底知识,考查运算求解能力、抽象与概括的能力、推理与论证的能力,考查数形结合的思想、转化与化归的思想、分类讨论的思想、有限与无限的思想. 解:(1)()2x f x e ax e '=+-,(1)200k f a a '===⇒=,故()x f x e e '=-1x ∴>时,()0f x '>,1x <时,()0f x '<,所以函数()f x 的增区间为(1,)+∞,减区间为(,1)-∞(2)设切点00(,)P x y ,那么切线000()()()y f x x x f x '=-+令000()()()()()g x f x f x x x f x '=---,因为只有一个切点,所以函数()g x 就只有一个零点,因为0()0g x =000()()()2()x x g x f x f x e e a x x '''=-=-+-,假设0,()0a g x '≥>0()()0g x g x >=,因此有唯一零点,由P 的任意性知0a ≥不合题意假设0a <,令00()2()xxh x e e a x x =-+-,那么0()0h x =()2x h x e a '=+,存在一个零点(ln(2),(ln 2))P a f a --,使曲线在该点处的切线与曲线只有一个公共点.故a 的取值范围为0a <. 25. 【命题意图】本试题考查了导数在研究函数中的运用.第一就是函数中有三角函数,要利用三角函数的有界性,求解单调区间.另外就是运用导数证明不等式问题的构造函数思想的运用.解:()sin f x a x '=-.(Ⅰ)因为[0,]x π∈,所以0sin 1x ≤≤.当1a ≥时,()0f x '≥,()f x 在[0,]x π∈上为单调递增函数; 当0a ≤时,()0f x '≤,()f x 在[0,]x π∈上为单调递减函数;当01a <<时,由()0f x '=得sin x a =,由()0f x '>得0arcsin x a ≤<或arcsin a x ππ-<≤;由()0f x '<得arcsin arcsin a x a π<<-.所以当01a <<时()f x 在[0,arcsin ]a 和[arcsin ,]a ππ-上为为单调递增函数;在[arcsin ,arcsin ]a a π-上为单调递减函数.(Ⅱ)因为()1sin cos 1sin 1sin cos f x x ax x x ax x x ≤+⇔+≤+⇔≤+- 当0x =时,01sin0cos00≤+-=恒成立当0x π<≤时,min 1sin cos 1sin cos 1sin cos []x x x xax x x a a x x+-+-≤+-⇔≤⇔≤令1sin cos ()(0)x xg x x xπ+-=<≤,那么又令()(1)cos (1)sin 1c x x x x x =++--,那么那么当3(0,)4x π∈时,sin cos 0x x +>,故()0c x '<,()c x 单调递减当3(,]4x ππ∈时,sin cos 0x x +<,故()0c x '≥,()c x 单调递增所以()c x 在(0,]x π∈时有最小值3()14c π=,而0lim ()(10)cos0(01)sin 010x c x +→=++--=,lim ()()(1)10x c x c πππ-→==-+-<综上可知(0,]x π∈时,()0()0c x g x '<⇒<,故()g x 在区间(0,]π单调递所以min 2[()]()g x g ππ==故所求a 的取值范围为2a π≤.另解:由()1sin f x x ≤+恒成立可得2()111f a a πππ≤⇔-≤⇔≤令2()sin (0)2g x x x x ππ=-≤≤,那么2()cos g x x π'=-当2(0,arcsin)x π∈时,()0g x '>,当2(arcsin,)2x ππ∈时,()0g x '< 又(0)()02g g π==,所以()0g x ≥,即2sin (0)2x x x ππ≤≤≤故当2a π≤时,有2()cos f x x x π≤+①当02x π≤≤时,2sin x x π≤,cos 1x ≤,所以()1sin f x x ≤+②当2x ππ≤≤时,22()cos 1()sin()1sin 22f x x x x x x ππππ≤+=+---≤+ 综上可知故所求a 的取值范围为2a π≤.【点评】试题分为两问,题词面比拟简单,给出的函数比拟新颖,因为里面还有三角函数,这一点对于同学们来说有点难度,不同于平时的练习题,相对来说做得比拟少.但是解决的关键还是要看导数的符号,求解单调区间.第二问中,运用构造函数的思想,证明不等式,一直以来是个难点,那么这类问题的关键是找到适宜的函数,运用导数证明最值大于或者小于零的问题得到解决.26. 【考点定位】此题应该说是导数题目中较为常规的类型题目,考查的切线、单调性、极值以及最值的问题都是课本中要求的重点内容,也是学生掌握比拟好的知识点.解:(1)由()1c ，为公共切点可得:2()1(0)f x ax a =+>,那么()2f x ax '=,12k a =, 3()g x x bx =+,那么2()=3g x x b '+,23k b =+,∴23a b =+①又(1)1f a =+,(1)1g b =+,∴11a b +=+,即a b =,代入①式可得:33a b =⎧⎨=⎩.(2)24a b =,∴设3221()()()14h x f x g x x ax a x =+=+++那么221()324h x x ax a '=++,令()0h x '=,解得:12a x =-,26ax =-;0a >,∴26a a-<-,∴原函数在2a ⎛⎫-∞- ⎪⎝⎭，单调递增,在26a a ⎛⎫-- ⎪⎝⎭，单调递减,在6a ⎛⎫-+∞ ⎪⎝⎭，上单调递增①假设12a--≤,即2a ≤时,最大值为2(1)4a h a =-;②假设126a a -<-<-,即26a <<时,最大值为12a h ⎛⎫-= ⎪⎝⎭③假设16a --≥时,即6a ≥时,最大值为12a h ⎛⎫-= ⎪⎝⎭. 综上所述:当(]02a ∈，时,最大值为2(1)4a h a =-;当()2,a ∈+∞时,最大值为12a h ⎛⎫-= ⎪⎝⎭. 27. 【解析】(I)设(1)xt e t =≥;那么2222111a t y at b y a at at at -'=++⇒=-= ①当1a ≥时,0y '>⇒1y at b at=++在1t ≥上是增函数得:当1(0)t x ==时,()f x 的最小值为1a b a++②当01a <<时,12y at b b at =++≥+当且仅当11(,ln )xat t e x a a ====-时,()f x 的最小值为2b +(II)11()()x xx x f x ae b f x ae ae ae'=++⇒=-由题意得:2222212(2)333131(2)222f ae b a ae e f ae b ae ⎧⎧=++==⎧⎪⎪⎪⎪⎪⇔⇔⎨⎨⎨'=⎪⎪⎪-==⎩⎪⎪⎩⎩。

全国各地高考试题分类解析导数部分

全国各地高考试题分类解析导数部分1、(广东卷)函数32()31f x x x=-+是减函数的区间为(D)（Ａ）(2,)+∞（Ｂ）(,2)-∞（Ｃ）(,0)-∞（Ｄ）(0,2)2.（全国卷Ⅰ）函数93)(23-++=xaxxxf，已知)(xf在3-=x时取得极值，则a=（B）（A）2 （B）3 （C）4（D）53.（湖北卷）在函数xxy83-=的图象上，其切线的倾斜角小于4π的点中，坐标为整数的点的个数是（ D ）A．3 B．2 C．14．(江西)已知函数()y xf x'='()f x是函数()f x的导函数)中()y f x=的图象大致是(C ）5.(浙江)函数y＝ax2＋1(A) 18(B)416.(重庆卷)曲线y=x3在点角形的面积为______8/3____。

7.（江苏卷）（14）曲线31y x x=++在点（1,3）处的切线方程是41y x=-8. ( 全国卷III)曲线32y x x=-在点（1，1）处的切线方程为x+y-2=09.（北京卷）过原点作曲线y＝e x的切线，则切点的坐标为(1,e)；，切线的斜率为e．10.(全国卷Ⅱ)设a为实数,函数.)(23axxxxf+--=(Ⅰ)求)(x f 的极值.(Ⅱ)当a 在什么范围内取值时,曲线x x f y 与)(=轴仅有一个交点.解：(I)'()f x =32x －2x －1若'()f x =0，则x ==－13，x =1当x 变化时，'()f x ，()f x 变化情况如下表：∴()f x 的极大值是()327f a -=+，极小值是(1)1f a =- (II)函数322()(1)(1)1f x x x x a x x a =--+=-++-由此可知，取足够大的正数时，有()f x >0，取足够小的负数时有()f x <0，所以曲线y =()f x 与x 轴至少有一个交点结合()f x 的单调性可知：当()f x 的极大值527a +<0，即5(,)27a ∈-∞-时，它的极小值也小于0，因此曲线y =()f x 与x 轴仅有一个交点，它在(1，+∞)上。

【2013备考】各地名校试题解析分类汇编(一)理科数学：1集合

各地解析分类汇编:集合与简易逻辑1【云南省玉溪一中2013届高三第四次月考理】已知:p “,,a b c 成等比数列”，:q “ac b =”，那么p 成立是q 成立的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又非必要条件【答案】D【解析】,,a b c 成等比数列,则有2b ac =，所以b =所以p 成立是q 成立不充分条件.当==0a b c =时，有ac b =成立，但此时,,a b c 不成等比数列，所以p 成立是q 成立既不充分又非必要条件，选D.2【云南省玉溪一中2013届高三上学期期中考试理】设全集{}1,2,3,4,5U =,集合{}2,3,4A =,{}2,5B =,则()U B C A =（）A.{}5B. {}125，，C. {}12345，，，，D.∅【答案】B【解析】{1,5}U C A =，所以()={1,5}{2,5}={1,2,5}U B C A ，选B.【解析】当k =0时，x =1；当k =1时，x =2；当k =5时，x =4；当k =8时，x =5，故选B. 4【云南师大附中2013届高三高考适应性月考卷（三）理科】已知条件2:340p x x --≤；条件22:690q x x m -+-≤ 若p是q的充分不必要条件，则m的取值范围是（）A．[]1,1- B．[]4,4- C．(][),44,-∞-+∞D．(][),11,-∞-+∞【答案】C【解析】14p x -：≤≤，记33(0)33(0)q m x m m m x m m -++-：≤≤＞或≤≤＜，依题意，03134m m m ⎧⎪--⎨⎪+⎩＞， ≤，≥或03134m m m ⎧⎪+-⎨⎪-⎩＜， ≤，≥，解得44m m -≤或≥.选C.5【云南省玉溪一中2013届高三第三次月考理】下列命题中正确的是( )A.命题“x R ∀∈，2x x -0≤”的否定是“2,0x R x x ∃∈-≥”B.命题“p q ∧为真”是命题“p q ∨为真”的必要不充分条件C.若“22am bm ≤，则a b ≤”的否命题为真 D.若实数,[1,1]x y ∈-，则满足221x y +≥的概率为4π. 【答案】C【解析】A 中命题的否定式2,0x R x x ∃∈->，所以错误.p q ∧为真，则,p q 同时为真，若p q ∨为真，则,p q 至少有一个为真，所以是充分不必要条件，所以B 错误.C 的否命题为“若22am bm >，则a b >”，若22am bm >，则有0,m a b ≠>所以成立，选C.6【天津市耀华中学2013届高三第一次月考理科】下列命题中是假命题的是 A 、(0,),>2x x sin x π∀∈ B 、000,+=2x R sin x cos x ∃∈C 、 ,3>0xx R ∀∈ D 、00,=0x R lg x ∃∈ 【答案】B【解析】因为000+4sin x cos x x π+≤（），所以B 错误，选B.7【天津市耀华中学2013届高三第一次月考理科】设a ，b ∈R ，那么“>1ab”是“>>0a b ”的A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件【答案】B【解析】由>1ab 得，10a a b b b --=>，即()0b a b ->，得0b a b >⎧⎨>⎩或0b a b <⎧⎨<⎩，即0a b >>或0a b <<，所以“>1ab ”是“>>0a b ”的必要不充分条件，选B.8【山东省烟台市莱州一中2013届高三10月月考（理）】集合{x x y R y A ,lg =∈=＞}{}2,1,1,2,1--=B 则下列结论正确的是A.{}1,2--=⋂B AB.()()0,∞-=⋃B A C RC.()+∞=⋃,0B AD.(){}1,2--=⋂B A C R【答案】D【解析】{0}A y y =>，所以={0}R C A y y ≤，所以(){}1,2--=⋂B A C R ，选D. 9【天津市天津一中2013届高三上学期一月考理】有关下列命题的说法正确的是A.命题“若x 2=1,则x=1”的否命题为:若“x 2=1则x ≠1” B.“1x =-”是“2560x x --=”的必要不充分条件C.命题“∃x ∈R,使得x 2+x+1<0”的否定是:“∀x ∈R,均有x 2+x+1<0” D.命题“若x=y,则sinx=siny ”的逆否命题为真命题【答案】D【解析】若x 2=1,则x=1”的否命题为21x ≠,则1x ≠，即A 错误。

各地名校试题解析分类汇编(一)理科数学：3导数1

2013年高考真题理科数学解析分类汇编3-导数

2019年高考真题和模拟题分项汇编数学(理)：专题03 导数及其应用 (含解析).docx

【2013备考】各地名校试题解析分类汇编(一)理科数学：3导数3

2021-2022年高考数学分项汇编 专题03 导数(含解析)理

【2013备考】各地名校试题解析分类汇编(一)理科数学：3导数1

【名师解析】高三名校数学理试题分省分项汇编专题03导数版含解析

高考数学各地名校试题解析分类汇编(一)3 导数1 理

(2019备考)各地名校试题解析分类汇编(一)理科数学：3导数2.doc

2021届高三名校数学理试题分省分项汇编 专题03 导数 Word版含解析

高考数学各地名校试题解析分类汇编(一)3 导数1 文

高考数学各地名校试题解析分类汇编(一)3 导数2 理

理科数学真题分类汇编专题3 导数的几何意义、定积分与微积分基本定理答案

【2013备考】各地名校试题解析分类汇编(一)理科数学：3导数1

2021年高考真题理科数学解析汇编导数与积分

全国各地高考试题分类解析导数部分

【2013备考】各地名校试题解析分类汇编(一)理科数学：1集合

2021-2022年高考数学分项汇编专题03 导数(含解析)理

2021届高三名校数学理试题分省分项汇编专题03 导数 Word版含解析