船舶静力学第三章初稳性(欧)
合集下载
船舶静力学:第3章 初稳性

1 2
y12dx
L/2 L / 2
1 2
y22dx
0
上式表示WL水线面对o-o轴的静矩为零,故该轴一定通过水线面的形心。 可见,两等体积水线面的交线必过原水线面的漂心(形心)。
二、浮心的移动
为便于研究浮心的移动,先介绍重心移动原理。 如图两物体W1,W2,重心为g,g1, 总的重心 为G,对g点取矩
由于 f 为小量
M R GM f
由复原力矩的方向,或G点和M点之间的关系,可以判断船舶平衡
的稳定性。
1)G在M之下, GM 为正值,MR为正值,与倾斜方向相反,外力消 失后可回复到原平衡位置,则原平衡状态为稳定平衡;
2)G在M之上, GM 为负值,MR为负值,与倾斜方向一致,外力消 失后,船舶在MR作用下继续倾斜,则原平衡状态为不稳定平衡; 3)G与M重合, GM 为零,MR为零,外力消失后,船舶不动,则原 平衡状态为中性平衡或随意平衡。
• >0 : 稳定平衡;=0:中性平衡;<0:不稳定平衡。
• 若系统处于稳定平衡状态,则:
F 0;M 0
P 2P l 0; l 2 0
• 打破平衡需要外力做功,或由外界输入的能量大于阀值H(h)。
船舶受外力矩作用,WL 不变,但形状变化,B
W1L1,W,G 不变,故▽大小 B1,复原力矩
M R GZ
t
aw1 w0
aw1
IT
2 3
L y3dx 2
0
3
L ( a )3 dx a3L
02
12
KB
1 2
w1a
BM IT a3L 1 a 12 atL 12w1
GM
KB BM
KG
1 2
第03章 初稳性

5/6
横倾 1 力矩
o
四、横倾1°力矩和横倾角计算 称船舶横倾1°(1/57.3)所需要的力矩为横倾1°力矩。
Mo GM 57.3
船舶在静横倾力矩MH 的作用下,引起的横倾角φ为: φ= MH / Mo ( °)
5°=0.08726; 10°=0.1745; 15°=0.2618;
sin5°=0.08715 sin10°=0.1736 sin15°=0.2588
p( x 2 x 1 ) GM L
新的首吃水dF’,尾吃水dA’分别为:
L d d F ( x f ) tg() 2 L ' d A d A ( x f ) tg() 2
' F
5/11
重量移动对浮态和稳性影响
重量p 从A(x1,y1,z1) 移动至A2(x2 ,y2,z2),排水量不变,
动稳性:外力矩突然作用,船舶横倾角速度不能忽 略时的稳性。动稳性主要是研究能量的转换与平衡问 题。(83.3甲1057驳在吴淞口被海轮碰撞1467吨生铁抛 入江中) 3/5
外力矩和复原力矩
五、外力矩和复原力矩 外力矩:包括风浪、船上货物(液体、谷物)移动、旅客 集中一舷、拖船急牵、拖网、火炮导弹发射、水流乱流、 回转等。它们是引起船舶倾斜的外部因素。 复原力矩:是船舶倾斜 后由重力和浮力产生的力 矩。它取决于船舶排水量、 重心高、浮心移动的距离、 横倾角。是内力。 4/5
2/2
二.浮心移动
系统质心移动原理:
考虑W=W1+W2 组成的系统,当W1从原位置移动到
新位置时,质心从g1移动到g1’,系统的质心也从G移 动到G’,且质心: 移动线:
' GG ' // g1g1 ' W1 g1g1 W
第03章-初稳性

2/5
静稳性和动稳性
四、静稳性和动稳性 Ø 静稳性:当外力矩缓慢作用,船舶横倾角速度很小时的 稳性。静稳性主要是研究力矩平衡问题。(86.4甲01004 和01007在青山锚地2*1200吨铁矿粉翻入江中) Ø 动稳性:外力矩突然作用,船舶横倾角速度不能忽 略时的稳性。动稳性主要是研究能量的转换与平衡问 题。(83.3甲1057驳在吴淞口被海轮碰撞1467吨生铁抛 入江中)
吐鲁番火焰山
1
3.1 概述
一、船舶稳性 Ø 船舶受到外力矩扰动产生倾斜后,是否会倾覆? Ø 外力矩消失后,船舶能否回复到原来的位置? 二、复原力矩
当船舶倾斜后,重力与浮力产生的力矩。 Mr = ΔGZ =f (船形,吃水,重心高,横倾角)
1/5
横倾与纵倾
三、横倾与纵倾 Ø 横倾:是指船体在左右舷方向的倾斜。由于受船宽的 限制,船舶提供的横向回复力矩小。船舶的横倾角大, 容易发生倾覆。 Ø 纵倾:是指船体在首尾方向的倾斜。由于船长大, 船舶提供的纵向回复力矩大,纵倾角一般都很小。(泰 坦尼克)
移动线: GG' //g1g1' 移动距离:GG' W1 g1g1' W
(与重量成反比 | 移动力矩相等)
1/3
浮心移动
同样,船体做等体积小角度横倾时,浮心移动服从:
BB1 //g1g2
B1B2v1o1g
其中 v1 og1是入水体积对倾斜轴 o-o 的静矩:
v 1 o 1 g L L // 2 2 1 2 y y( t) d g 3 2 x y t( g )1 3 L L // 2 2 y 3 dx
积分
L/ 2 L/ 2
1 2
y12dx
和
L/2 L/ 2
静稳性和动稳性
四、静稳性和动稳性 Ø 静稳性:当外力矩缓慢作用,船舶横倾角速度很小时的 稳性。静稳性主要是研究力矩平衡问题。(86.4甲01004 和01007在青山锚地2*1200吨铁矿粉翻入江中) Ø 动稳性:外力矩突然作用,船舶横倾角速度不能忽 略时的稳性。动稳性主要是研究能量的转换与平衡问 题。(83.3甲1057驳在吴淞口被海轮碰撞1467吨生铁抛 入江中)
吐鲁番火焰山
1
3.1 概述
一、船舶稳性 Ø 船舶受到外力矩扰动产生倾斜后,是否会倾覆? Ø 外力矩消失后,船舶能否回复到原来的位置? 二、复原力矩
当船舶倾斜后,重力与浮力产生的力矩。 Mr = ΔGZ =f (船形,吃水,重心高,横倾角)
1/5
横倾与纵倾
三、横倾与纵倾 Ø 横倾:是指船体在左右舷方向的倾斜。由于受船宽的 限制,船舶提供的横向回复力矩小。船舶的横倾角大, 容易发生倾覆。 Ø 纵倾:是指船体在首尾方向的倾斜。由于船长大, 船舶提供的纵向回复力矩大,纵倾角一般都很小。(泰 坦尼克)
移动线: GG' //g1g1' 移动距离:GG' W1 g1g1' W
(与重量成反比 | 移动力矩相等)
1/3
浮心移动
同样,船体做等体积小角度横倾时,浮心移动服从:
BB1 //g1g2
B1B2v1o1g
其中 v1 og1是入水体积对倾斜轴 o-o 的静矩:
v 1 o 1 g L L // 2 2 1 2 y y( t) d g 3 2 x y t( g )1 3 L L // 2 2 y 3 dx
积分
L/ 2 L/ 2
1 2
y12dx
和
L/2 L/ 2
第03章 初稳性解读

随遇平衡
2/6
初稳性高与横摇固有周期
三、初稳性高与船舶横摇固有周期Tφ的关系(补充)
T 0 . 58 f B
2
4 KG GM
0
B:船宽
f=f(B/d):修正系数(d:吃水)
KG: 船舶重心高度 GMo: 未经自由液面修正的初稳性高。 可见,过大的初稳性高使船舶横摇周期小,横摇剧 烈;因此应在保证船舶有足够的稳性的前提下,取较 小的初稳性高。(黄河9号采用高位水舱) 3/6
3
2
1 3
y 1 dx
3
)
v 1 og
1
L/2
L /2
1 2
y ytg ( ) dx
2 3
y tg ( )
1 3
L/2
L /2
y dx
3
3/3
三.横稳心及稳心半径
船舶小角度横倾时,浮心移动的轨迹,可视为圆心在
M点,半径为 BM 的圆弧的一部分。浮力ω▽作用线通
过M点。称M点为稳心;BM为稳心半径。
1 2 1 2
y 1 dx y 2 dx
2
2
v1=v2
1/2
等体积倾斜水线
积分
L/2
1 2
L /2
2 y 1 dx
和
L/2
1 2
L /2
y 2 dx 分别表示水线面WL
2
在轴线 o-o 两侧的面积对该轴线的静矩。由于横倾后排 水体积不变,应有V1=V2,即水线面对o-o 轴的静矩= 0, 所以等体积倾斜水线面与原水线面交线 o-o 通过水线面 漂心F。
动稳性:外力矩突然作用,船舶横倾角速度不能忽 略时的稳性。动稳性主要是研究能量的转换与平衡问 题。(83.3甲1057驳在吴淞口被海轮碰撞1467吨生铁抛 入江中) 3/5
第三章 稳性

船舶稳性的定义
一、船舶的三种平衡状态
1)重心G在稳心M之下,复原力矩与倾侧力矩反向,正浮时的船 舶处于稳定平衡状态。 稳心M:正浮时浮力作用线和微倾后浮力作用线的交点
一、船舶的三种平衡状态
2)重心G在稳心M之上,复原力矩与倾侧力矩同向,正浮时的船 舶处于不稳定平衡状态。
一、船舶的三种平衡状态
Байду номын сангаас
第二节 初稳性
横稳心(Transverse metacenter)M——船舶横向微幅倾斜后的 浮力作用线与正浮时的浮力作用线的交点。
第二节 初稳性
一、船舶初稳性的基本标志
一、船舶初稳性的基本标志
1.船舶微倾,θ<10~15° 2.等容倾斜,即倾斜前后排水量不变 3.倾斜轴通过初始水线面的面积中心,即漂心F 4.当排水量一定时,船舶的稳心M点为一定点 5.浮心B沿着以稳心M 为圆心,以稳心半径(横稳心半径BM )。 r 为半 径的圆弧轨迹移动
KG0
P Z
i
i
(m)
式中,Pi——船舶各组成部分的重量(包括空船、货物、航次储 备、船舶常数) (t) Zi——Pi相应的中心重心距基线高度 (m) Σ PiZi ——垂向重量力矩 (9.81kN.m)
1)空船重量及其重心高度的查取
对于某一船舶,空船重量及其重心高度为定值,它们可在船舶稳性计算 资料中查找。
2)货物重心高度Zi的确定
将均匀货物(积载因数SF相同或相近)的体积中心作为货物 重心看待。
近似公式计算法 Zi=货高/2 + 货物底端距基线距离 估算法 平行中体部位的舱室,货物重心取在货高的1/2处;首、尾部 位的舱室,货物重心取在货高的0.54~0.58处。 利用舱容曲线图确定载荷的重心高度
船舶静力学初稳性
20
▪ 二、重量的横向移动
Hale Waihona Puke 2020/5/23轮机工程学院
21
2020/5/23
轮机工程学院
22
▪ 三、重量的纵向移动
2020/5/23
轮机工程学院
23
2020/5/23
轮机工程学院
24
▪ 四、重量沿任意方向的移动
2020/5/23
轮机工程学院
25
2020/5/23
轮机工程学院
26
2020/5/23
8
▪ 三、稳心及稳心半径
▪ M点称为横稳心 (或初稳心)。
▪ BM称为横稳心 半径(或初稳心 半径)。
2020/5/23
轮机工程学院
9
▪ 纵稳心半径
2020/5/23
轮机工程学院
10
§3-3 初稳心公式和稳心高
▪ 一、初稳心公式
2020/5/23
▪ GZ复原力臂。
▪ GM横稳心高,也称 初稳心高。
▪ 3、船型系数曲线4条。
2020/5/23
轮机工程学院
17
2020/5/23
轮机工程学院
18
§3-5 重量移动对船舶浮态和初 稳心的影响
▪ 一、重量的垂直移动
2020/5/23
轮机工程学院
19
结论:提高船舶的重心对稳性不 利;降低船舶的重心是提高船舶 稳性的有效措施之一。
2020/5/23
轮机工程学院
2020/5/23
轮机工程学院
2
§3-2 浮心的移动和稳心及稳心半径
▪ 一、 等体积倾斜水线
2020/5/23
轮机工程学院
3
▪ 1、入水楔形的体积
第三章 稳性汇总

用不仅产生角位移,而且产生角加速度时的稳性。
三、船舶稳性的分类
3、按倾斜角大小分 (1)初稳性(Initial stability)——倾斜角小于15且干舷甲板边
缘开始入水前的稳性。 (2)大倾角稳性(Stability at large angle of inclination)
——倾斜角大于15或干舷甲板边缘开始入水后的稳性。 4、按船舱是否进水分类
第三章 保证船舶具有适度的稳性
教学要求
掌握船舶稳性的基本概念分类及其与船舶平衡的关系 ; 掌握初稳性、大倾角稳性和动稳性的表示方法和校核方
法; 了解静稳性曲线图和动稳性曲线图的特征和应用 掌握船舶稳性的要求; 掌握船舶稳性的检验和调整方法。
❖ 学时:10学时
重点和难点
❖ 重点
船舶稳性(初稳性、大倾角稳性和动稳性)的表 示和核算方法;
KG0
Pi Zi
(m)
❖ 式中,Pi——船舶各组成部分的重量(包括空船、货物、航次储
备、船舶常数)
(t)
❖
Zi——Pi相应的中心重心距基线高度 (m)
❖ Σ PiZi ——垂向重量力矩 (9.81kN.m)
1)空船重量及其重心高度的查取
❖ 对于某一船舶,空船重量及其重心高度为定值,它们可在船舶稳性计算 资料中查找。
船舶稳性的定义
一、船舶的三种平衡状态
1)重心G在稳心M之下,复原力矩与倾侧力矩反向,正浮时的 船舶处于稳定平衡状态。
稳心M:正浮时浮力作用线和微倾后浮力作用线的交点
一、船舶的三种平衡状态
2)重心G在稳心M之上,复原力矩与倾侧力矩同向,正浮时的 船舶处于不稳定平衡状态。
一、船舶的三种平衡状态
3)重心G在稳心M重合,复原力矩等于0,正浮时的船舶处于随 遇稳定平衡状态。
三、船舶稳性的分类
3、按倾斜角大小分 (1)初稳性(Initial stability)——倾斜角小于15且干舷甲板边
缘开始入水前的稳性。 (2)大倾角稳性(Stability at large angle of inclination)
——倾斜角大于15或干舷甲板边缘开始入水后的稳性。 4、按船舱是否进水分类
第三章 保证船舶具有适度的稳性
教学要求
掌握船舶稳性的基本概念分类及其与船舶平衡的关系 ; 掌握初稳性、大倾角稳性和动稳性的表示方法和校核方
法; 了解静稳性曲线图和动稳性曲线图的特征和应用 掌握船舶稳性的要求; 掌握船舶稳性的检验和调整方法。
❖ 学时:10学时
重点和难点
❖ 重点
船舶稳性(初稳性、大倾角稳性和动稳性)的表 示和核算方法;
KG0
Pi Zi
(m)
❖ 式中,Pi——船舶各组成部分的重量(包括空船、货物、航次储
备、船舶常数)
(t)
❖
Zi——Pi相应的中心重心距基线高度 (m)
❖ Σ PiZi ——垂向重量力矩 (9.81kN.m)
1)空船重量及其重心高度的查取
❖ 对于某一船舶,空船重量及其重心高度为定值,它们可在船舶稳性计算 资料中查找。
船舶稳性的定义
一、船舶的三种平衡状态
1)重心G在稳心M之下,复原力矩与倾侧力矩反向,正浮时的 船舶处于稳定平衡状态。
稳心M:正浮时浮力作用线和微倾后浮力作用线的交点
一、船舶的三种平衡状态
2)重心G在稳心M之上,复原力矩与倾侧力矩同向,正浮时的 船舶处于不稳定平衡状态。
一、船舶的三种平衡状态
3)重心G在稳心M重合,复原力矩等于0,正浮时的船舶处于随 遇稳定平衡状态。
第03章 初稳性.

第三章 初稳性
3.1 概述 3.2 浮心移动,稳心 3.3 初稳性和稳性高 3.4 静水力曲线 3.5 重量移动对浮态和稳性的影响 3.6 装卸载荷对浮态和稳性的影响 3.7 自由液面对稳性的影响 3.8 悬挂重物对稳性的影响 3.9 船舶进坞和搁浅稳性 3.10 船舶完整稳性校核 3.11 船舶倾斜试验 吐鲁番火焰山 作业
2/2
二.浮心移动
系统质心移动原理:
考虑W=W1+W2 组成的系统,当W1从原位置移动到
新位置时,质心从g1移动到g1’,系统的质心也从G移 动到G’,且质心: 移动线:
' GG ' // g1g1 ' W1 g1g1 W
移动距离: GG '
(与重量成反比 | 移动力矩相等)
1/3
浮心移动
3 1 1 2 2 1 3 3 1
v1 og1
1 L / 2 2
L/ 2
y ytg()dx y tg()
2 3
L/ 2 1 3 L / 2
y3dx
3/3
三.横稳心及稳心半径
船舶小角度横倾时,浮心移动的轨迹,可视为圆心在
M点,半径为 BM 的圆弧的一部分。浮力ω▽作用线通
3.1 概述
一、船舶稳性 船舶受到外力矩扰动产生倾斜后,是否会倾覆? 外力矩消失后,船舶能否回复到原来的位置? 二、复原力矩 当船舶倾斜后,重力与浮力产生的力矩。 Mr = ΔGZ =f (船形,吃水,重心高,横倾角)
1/5
横倾与纵倾
三、横倾与纵倾
横倾:是指船体在左右舷方向的倾斜。由于受船宽 的限制,船舶提供的横向回复力矩小。船舶的横倾角 大,容易发生倾覆。
2/6
3.1 概述 3.2 浮心移动,稳心 3.3 初稳性和稳性高 3.4 静水力曲线 3.5 重量移动对浮态和稳性的影响 3.6 装卸载荷对浮态和稳性的影响 3.7 自由液面对稳性的影响 3.8 悬挂重物对稳性的影响 3.9 船舶进坞和搁浅稳性 3.10 船舶完整稳性校核 3.11 船舶倾斜试验 吐鲁番火焰山 作业
2/2
二.浮心移动
系统质心移动原理:
考虑W=W1+W2 组成的系统,当W1从原位置移动到
新位置时,质心从g1移动到g1’,系统的质心也从G移 动到G’,且质心: 移动线:
' GG ' // g1g1 ' W1 g1g1 W
移动距离: GG '
(与重量成反比 | 移动力矩相等)
1/3
浮心移动
3 1 1 2 2 1 3 3 1
v1 og1
1 L / 2 2
L/ 2
y ytg()dx y tg()
2 3
L/ 2 1 3 L / 2
y3dx
3/3
三.横稳心及稳心半径
船舶小角度横倾时,浮心移动的轨迹,可视为圆心在
M点,半径为 BM 的圆弧的一部分。浮力ω▽作用线通
3.1 概述
一、船舶稳性 船舶受到外力矩扰动产生倾斜后,是否会倾覆? 外力矩消失后,船舶能否回复到原来的位置? 二、复原力矩 当船舶倾斜后,重力与浮力产生的力矩。 Mr = ΔGZ =f (船形,吃水,重心高,横倾角)
1/5
横倾与纵倾
三、横倾与纵倾
横倾:是指船体在左右舷方向的倾斜。由于受船宽 的限制,船舶提供的横向回复力矩小。船舶的横倾角 大,容易发生倾覆。
2/6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
船舶的横向倾斜——向左舷或向右舷一侧的
倾斜(横倾),倾斜力矩(横倾力矩)的作用平 面平行于中横剖面;
船舶的纵向倾斜——向船首或向船尾的倾斜
(纵倾),倾斜力矩(纵倾力矩)的作用平面平 行于中纵剖面。
横稳性和纵稳性——研究船舶抵抗横向 和纵向倾斜的能力
静稳性——倾斜力矩的作用是从零开始
逐渐增加,使船舶倾斜时的角速度很小, 可忽略不计;
WL→WL1时浮心B→B1,将浮心的轨迹假设为一圆弧,圆心为M,
半径为 BM 。这样,在倾斜过程中浮力作用线均过M点。 M~横稳心(初稳心), BM ~横稳心半径(初稳心半径)
BB1
IT
M
当 为微小角度时,
W
W
W1
L1
BB1 BB1 BM
G
B
B1
L
BM IT (3-7)
适用范围:=10º~15º的小角度情况。
动稳性——倾斜力矩是突然作用在船上,
使船舶倾斜有明显的角速度的变化。
初稳性(小倾角稳性)——倾斜角度小于 10°~15°或上甲板边缘开始入水前的稳性。
大倾角稳性(大倾角横稳性)——倾斜角度大于 10°~15°或上甲板边缘开始入水后的稳性。
划分原因:小倾角稳性可引入某些假定,既使浮态合 计被简化,又能较明确地获得影响初稳性的各种因素 之间的规律。
2V1
g1o
2 3
Байду номын сангаас
L/2 L/ 2
y3dx
IT
IT
2 3
L / 2 y3dx
L/2
IT是WL水线面对于0-0 轴的横向惯性矩
BB1
IT
(3-6)
g2
v1
O
g1
L1
B
B1 v2
L
dx
L1
y1tg
o
L
2y/3
y2
BB1
IT
(3-6)
浮心的移动距离BB1与横向惯性矩IT、 横倾角 成正比,而与排水体积成成反比。
倾斜力矩
倾斜力矩(矛盾外因) 造成船舶倾斜,这取决于
外界条件
复原力矩
复原力矩(矛盾内因) 取决于排水量、重心高 度及浮心移动的距离等 因素
船舶倾覆
外因通过内因起作用!
稳性问题是着重研究和计算这一矛盾的内因 (复原力矩计算)及其有关的影响因素
a) 倾斜力矩的来源 (1)风浪的作用; (2)船上货物的移动; (3)旅客集中于某一船舷。 (4)拖船的急牵,火箭的发射
船舶稳性——船舶在外力作用下偏离其平衡位置而 倾斜,当外力消失后,能自行回复到原来平衡位置 的能力。
是否与不倒翁类似?
左舷
右舷
阵 风
0
无外力的作用 W
G
B
船舶受外力矩作用,WL W1L1, W,G 不变,故▽大小不变,但形状
变化,B
B1,
浮力 和重力W形成一个力偶MR,
MR=·GZ
称为复原力矩 GZ称为复原力臂
3-1 概述 3-2 浮心的移动,稳心及稳心半径 3-3 初稳性公式,稳性高 3-4 船舶静水力曲线图 3-5 重量移动对船舶浮态及初稳性的影响 3-6 装卸载荷对船舶浮态及初稳性的影响 3-7 自由液面对船舶初稳性的影响 3-8 悬挂重量对船舶初稳性的影响 3-9 船舶进坞及搁浅时的稳性 3-10 船舶在各种装载下浮态及初稳性的计算 3-11 船舶倾斜试验 复习思考题
V1 g1o
L/ 2 1 y2tg dx 2 y 1 tg
2 L / 2
33
L / 2 y3dx
L/ 2
dx
L1
y1tg
o
L
2y/3
y2
V1 g1o
L/ 2 1 y2tg dx 2 y 1 tg
2 L / 2
33
L / 2 y3dx
L/ 2
W
W1
对于微小角度的横倾,有tg
对于=10º~15º的小角度情况,相当于:
W g2
W1
v1
O
g1
L1
B
B1 v2
L
利用重心移动原理, 船舶倾 斜后浮心的移动距离为:
W
BB1
g1 g2
V2
且BB1 / / g1 g2
W1
由于V1 V2 ,
1 g1o g2o 2 g1g2
g2
v1
O
g1
L1
B
B1 v2
L
BB1
2g1o
V1
V1 g1o是入水楔形体积对轴线O-O的静矩
1 2
y22dx
因为等体积倾斜 V1 V2
L/2 L/ 2
1 2
y12dx
L/2 L/ 2
1 2
y22dx
L / 2 L / 2
1 2
y12dx
L/2 L / 2
1 2
y22dx
(3-2)
上式表示水线面WL在O-O两侧面积对轴线O-O的静矩
相等, 即整个水线面WL对O-O的面积静矩为零,亦 即轴线O-O通过水线面WL的形心(或称漂心)。
b) 复原力矩 复原力矩大小取决于排水量、重心高度、浮心
移动的距离等因素。
讨论稳性问题 (1)确定倾斜水线的位置。 (2)找出浮心和浮力作用线的位置。 (3)确定复原力矩的大小及方向。
一、等体积横倾
船舶受倾斜力矩作用发生倾斜,水线WL W1L1。排水体积保 持不变,W1L1是等体积倾斜水线。φ为小角度。入水楔形为 LOL1,出水楔形WOW1。
三角形LOL1的面积
1 2
y12tg
W
W1
v2
O
y2
v1
y1
L1
沿船长取dx一小段,其体积dV1
1 2
y12tgdx
L 整个入水楔形体积
dx
L1
y1tg
o
L
y2
V1
L/2 L/ 2
1 2
y12tg
dx
tg
L/2 L/ 2
1 2
y12dx
同理:出水楔形体积为V2 tg
L/2 L/ 2
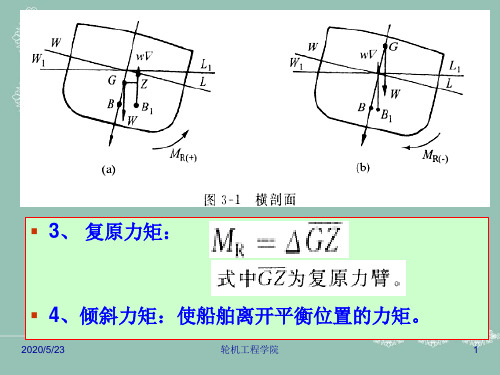
复原力矩
MR (+)
复原力矩 MR (-)
W
W
W
W1
L1
G
B
Z B1
W1
L
G
W
L1
B B1
L
MR (+)
MR (-)
W
W
W
W1
L1
G
B
Z B1
L
W1
G
W
L1
B B1
L
(1)图中复原力距,倾斜力矩方向相反,起到抵抗倾斜力矩的作 用,MR定为正值
(2)图中复原力距,倾斜力矩方向相同,倾斜力矩增加,MR定为 负值
W1 g1
WG
g
W2
G1
g2
从而
W1 Gg G1g W gg1 gg2
所以 g1gg2 与 GgG1 相似,故有
GG1 Gg W1 g1g2 gg1 W
GG1
W1 W
g1g2
上式表明:整个系统的重心移动方向平行于局部重心
的移动方向,且重心的移动距离GG1与总重量W成反 比,与局部重量W1成正比。
水线面 WL
o
y1
y1/2
o
y2
dx
L
dx
L1
y1tg
o
L
y2
重要结论:
两等体积水线面的交线o-o 必然通过原水线面 WL的漂心(同样适用于纵倾的情况)。
系统总重量: W = W1+W2
如图两物体W1,W2,重心为g1,g, 总 的重心为G,对g点取矩,W Gg W1 gg1
W1由 g1 移动到 g2 后, W G1g W1 gg2
