第 2 章 二阶张量
合集下载
第二章 张量(清华大学弹塑性力学)

利用爱因斯坦求和约定,写成:
xi aij x j
其中 j 是哑指标,i 是自由指标。
19
Appendix A.1
张量基本概念
★ 在表达式或方程中自由指标可以出现多次,但不得
在同项内出现两次,若在同项内出现两次则是哑指 标。例:
若i为自由指标
ji , j fi 0
ji , j fii 0
个独立的自由指标,其取值范围是1~n,则这个方
程代表了nk 个分量方程。在方程的某项中若同时出 现m对取值范围为1~n的哑指标,则此项含相互迭
加的nm个项。
27
Appendix A.1
张量分析初步
矢量和张量的记法,求和约定 符号ij与erst 坐标与坐标转换 张量的分量转换规律,张量方程 张量代数,商判则
3. 换标符号,具有换标作用。例如:
d s2 ij d xi d x j d xi d xi d x j d x j
即:如果符号的两个指标中,有一个和同项中其它 因子的指标相重,则可以把该因子的那个重指标换成 的另一个指标,而自动消失。
30
Appendix A.2
符号ij与erst
Appendix A.1
张量基本概念
★ 指标符号也适用于微分和导数表达式。例如,三维
空间中线元长度 ds 和其分量 dxi 之间的关系
d s d x1 d x2 d x3
2 2 2
2
2 可简写成: d s d xi d xi
场函数 f(x1, x2, x3) 的全微分:
21n1 22n2 23n3 T2
31n1 32n2 33n3 T3
18
xi aij x j
其中 j 是哑指标,i 是自由指标。
19
Appendix A.1
张量基本概念
★ 在表达式或方程中自由指标可以出现多次,但不得
在同项内出现两次,若在同项内出现两次则是哑指 标。例:
若i为自由指标
ji , j fi 0
ji , j fii 0
个独立的自由指标,其取值范围是1~n,则这个方
程代表了nk 个分量方程。在方程的某项中若同时出 现m对取值范围为1~n的哑指标,则此项含相互迭
加的nm个项。
27
Appendix A.1
张量分析初步
矢量和张量的记法,求和约定 符号ij与erst 坐标与坐标转换 张量的分量转换规律,张量方程 张量代数,商判则
3. 换标符号,具有换标作用。例如:
d s2 ij d xi d x j d xi d xi d x j d x j
即:如果符号的两个指标中,有一个和同项中其它 因子的指标相重,则可以把该因子的那个重指标换成 的另一个指标,而自动消失。
30
Appendix A.2
符号ij与erst
Appendix A.1
张量基本概念
★ 指标符号也适用于微分和导数表达式。例如,三维
空间中线元长度 ds 和其分量 dxi 之间的关系
d s d x1 d x2 d x3
2 2 2
2
2 可简写成: d s d xi d xi
场函数 f(x1, x2, x3) 的全微分:
21n1 22n2 23n3 T2
31n1 32n2 33n3 T3
18
第2章 张量分析(清华大学张量分析,你值得拥有)

( Nij ij )a j 0 det( Nij ij ) 0
利用指标升降关系 a为非0矢量 利用主不变量
N ( ) 3 J1N 2 J 2 J3N 0
二阶张量的标准形: 张量最简单的形式
非对称二阶张量
•
请研究以下领域的同学关注。 1、应变梯度理论,偶应力理论 2、电流场,电磁流变(有旋场)
x
x
椭圆曲线的坐标变换
正交变换可使椭圆曲线的方程由以下一般形式
ax bxy cy d 0
任意二阶张量将一线性相关的矢量集映射为线性相 关的矢量集:
(i)u(i) 0
i 1
l
l l 0 T (i)u(i) (i)(T u(i)) i 1 i 1
正则与退化的二阶张量
•
3D空间中任意二阶张量T将任意矢量组u,v,w映射 为另一矢量组,满足:
N S
1 p
S S1e1e1 S2e2e2 S3e3e3
Si N i
1 p
几种特殊的二阶张量
正张量的对数
N N1e1e1 N2e2e2 N3e3e3
ln N ln N1 e1e1 ln N2 e2e2 ln N3 e3e3
Nij N ji Ni j Nij Nij N ji N ij N ji
N 1 NT 1
( ) , ( ) , ( ) ,
N T 1 N 2 N T 3 N 3 N T 2 N 4
NT 4
N T ( 4 )
反对称张量与其转置张量分量及二者所对应的矩阵
二阶张量的行列式
连续介质力学第二章.

即得( i ),将( i )作相应的指标替换, 展开化简,将得其余三式。
二维置换符号 e (, 1, 2)
从三维退化得到
e ei j3 e 3
其中
e11 e22 0, e12 e21 1
有下列恒等式
e e
又如,方程
12
2 2
32
111
2 22
333
用指标法表示,可写成
i i i ii i ii i ii
i 不参与求和,只在数值上等于 i
1.2 Kronecker 符号
在卡氏直角坐标系下,Kronecker 符号定义为:
ij
表示
e1 A11e1 A12e2 A13e3 e2 A21e1 A22e2 A23e3 e3 A31e1 A32e2 A33e3
ei Aije j i 为自由指标,j 为哑标
表示
e1 A11e1 A12e2 A13e3 e2 A21e1 A22e2 A23e3 e3 A31e1 A32e2 A33e3
新旧基矢量夹角的方向余弦:
ei e j | ei || e j | cos(ei , e j ) cos(ei , e j ) ij
1.5.1 坐标系的变换关系
ij cos(ei , e j ) ei e j
旧 新
e1
e 2 e 3
e1
11 21 31
ai xi a1x1 a2 x2 a3x3 bjj b11 b22 b33
cmem c1e1 c2e2 c3e3
双重求和
33
S
张量分析提纲及部分习题答案

y
对静止的连续介质,有
ζ n fd 0 , ζd fd 0 ,
A
ζ f 0。
(21) 证明应力是一个张量; 记 ij :表示在给定基 g i 下,在面 g j 上,单位面积受力 F j 在 g i 方向上的分量为
对斜圆锥面上任一点 (图中黑点处) , 不难由相似三角形得到,
z z R cos C i R sin j zk ,进而可得, H H r Rz sin zR cos r R cos C R g i j, gz i sin j k , H H z H H r
dx g dx I g dx II 1 4 x I 2 dx I 6 x I x II 2 dx II Pdx I Q dx II 11 12 1 1 I 。 2 4 dxII g 21dx I g 22 dx II 6 x I x II dx I 9 x II dx II P2 dx I Q2 dx II
Pi Qi 时,坐标 xI , xII 才可能存在。即向量场 P, Q 无旋时,其在两点间 x II x I Pi Qi 的路径积分与路径无关,积出的值就是坐标。本例中, II I ,故相应的“协 x x
当 变坐标”不存在。 (正因为如此,坐标也没有逆变、协变之说。 ) (9) 有点类似曲面第一基本型(1.3.12) 。 (10) Lame 常数定义(1.3.13)在非正交系中也成立,但此时(1.3.12a)不成立。
1.9-1.13:略; 1.14: 注意,所谓斜圆锥是指, O 点沿 z 方向在大圆平面上的投影 M 在大圆的直径上。
第二章-张量基础

5
例 2. 张量。
ai 和 bi 是两个任意矢量, ij ai b j 是标量。证明 ij 是一个二阶
证:由于 是一个标量,即坐标变换时的不变量,故
ij ai b j ij (ii ai )( jj b j ) ii jjij aib j ij aib j
为一个二阶张量。事实上
(2.21)
Cij Aij Bij ii jj Aij ii jj Bij
ii jj ( Aij Bij ) ii jj Cij
式(2.21)也可以写成 C Cij ei e j A B ( Aij Bij )ei e j 。 张量的线性组合满足加法交换律 A B B A 、结合律
T21e2 e1 T22e 2 e 2 T23e2 e3
T31e3 e1 T32e3 e 2 T33e3 e3
二阶的基张量有 9 个。需要指出的是,若 i j ,则 ei
e j e j ei 。
3
张量的第二种定义 在某一坐标系中,某一个量 T 可表示成 T Ti1i2 in ei1 ei2 ein 的形式, 则就称 T 是一个 n 阶张量。 可以证明,该定义和(2.19)式的定义是等价的:
(c)
Cij ii jj Cij ii jj Aijkl Bkl ii jj k k l l Aijkl Bk l
(b)-(c)得: ( Aijk l ii jj k k l l Aijkl ) Bk l 0 由于 Bk l 是任意的,从上式可得: Aij k l 上式表明, Aijkl 为一个四阶张量。
T Ti1i2 in ei1 ei2 ein Ti1i2 in i1i1 ei1 i2 i2 ei2 in in ein i1i1 i2 i2 in in Ti1i2 in ei1 ei2 ein Ti1i2 in ei1 ei2 ein
弹性力学-第二章 张量基础知识

′ x1 = a11 x1 + a12 x2 + a13 x3
′ x2 = a21 x1 + a22 x2 + a23 x3 ′ x3 = a31 x1 + a32 x2 + a33 x3
张量基础知识§ 第二章 张量基础知识§2-1
坐标系和矢量
e′ = Aije j i
表示
i 为自由指标,j 为哑标 为自由指标,
x3
(2.2)
e3 x1
e1 e2
x2
张量基础知识§ 第二章 张量基础知识§2-1
坐标系和矢量
A:求和约定、 A:求和约定、哑指标 求和约定 S = a1 x1 + a2 x2 + ⋯ an xn
= ∑ ai xi = ∑ a j x j = ∑ ak xk
i =1 j=1 k =1 n n n
显然, 与求和无关,可用任意字母代替。 显然,指标 i, j, k 与求和无关,可用任意字母代替。 为简化表达式,引入Einstein求和约定: Einstein求和约定 为简化表达式,引入Einstein求和约定:每逢某个指 标在一项中重复一次 就表示对该指标求和, 重复一次, 标在一项中重复一次,就表示对该指标求和,指标取 遍正数1 这样重复的指标称为哑标 哑标。 遍正数1,2,…,n。这样重复的指标称为哑标。 于是 or or
i, j, k为顺序排列 为顺序排列 i, j, k为逆序排列 为逆序排列 i, j, k有两个相等 有两个相等 (2.5)
例如: 例如:
e123 = e231 = e312 = 1 e321 = e213 = e132 = −1 e111 = e121 = e232 = ⋯ = 0
连续介质力学第二章
T ip eie p
其中: T ip ekjp jTik
小 结:
哈密顿算子
梯度
i ei gradf f eii f
散度
diva a iai
旋度
curla a
2.2 Laplace算子
公式:
2 f f
展开后有:
原式 (i ei ) ( j f ej ) (i j f )ij
第二章 张量分析
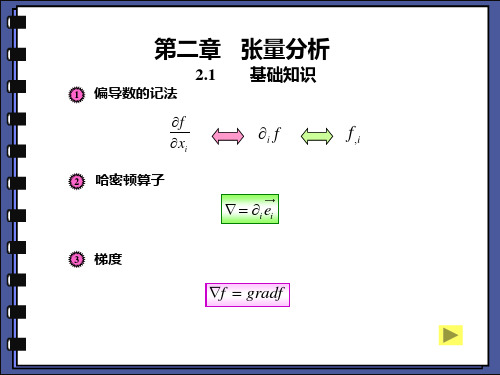
2.1 基础知识
1 偏导数的记法
f
xi
i f
f,i
2 哈密顿算子
i ei
3 梯度
f gradf
标量的梯度:
标量函数:
f f (r)
则梯度为:
f gradf eii f 展开后有: 原式 1 f e1 2 f e2 3 f e3
f i f j f k x y z
a (P、Q、R)
根据Gauss定理有:
左边 (a1n1 a2n2 a3n3)dS S ainidS S
a ndS a d S
S
S
右边 (1a1 2a2 3a3)dV V
iaidV adV
V
V
a d S adV
S
V
2 Stokes定理
Pdx Qdy Rdz
ii f 11 f 22 f 33 f
2 f 2 f 2 f
x2 y2 z2
2.3 物质导数
若 f f (t, r(t))
则:Df f f r f f x f y f z
Dt t r t t x t y t z t
f
x
y
z
t (1 f ) t (2 f ) t (3 f ) t
S
(1a2 2a1)dl1dl2 ]
其中: T ip ekjp jTik
小 结:
哈密顿算子
梯度
i ei gradf f eii f
散度
diva a iai
旋度
curla a
2.2 Laplace算子
公式:
2 f f
展开后有:
原式 (i ei ) ( j f ej ) (i j f )ij
第二章 张量分析
2.1 基础知识
1 偏导数的记法
f
xi
i f
f,i
2 哈密顿算子
i ei
3 梯度
f gradf
标量的梯度:
标量函数:
f f (r)
则梯度为:
f gradf eii f 展开后有: 原式 1 f e1 2 f e2 3 f e3
f i f j f k x y z
a (P、Q、R)
根据Gauss定理有:
左边 (a1n1 a2n2 a3n3)dS S ainidS S
a ndS a d S
S
S
右边 (1a1 2a2 3a3)dV V
iaidV adV
V
V
a d S adV
S
V
2 Stokes定理
Pdx Qdy Rdz
ii f 11 f 22 f 33 f
2 f 2 f 2 f
x2 y2 z2
2.3 物质导数
若 f f (t, r(t))
则:Df f f r f f x f y f z
Dt t r t t x t y t z t
f
x
y
z
t (1 f ) t (2 f ) t (3 f ) t
S
(1a2 2a1)dl1dl2 ]
弹性力学第二章

强调指出:张量必须满足坐标变换,否则不能视为张量。也就是 说,从一个坐标系旋转到另一个新的坐标系,张量的表达形式不变。 即应有:T
= Ti1i2 ⋅⋅⋅in ei1 ⊗ ei2 ⊗ ⋅⋅⋅ ⊗ ein = Ti1i2 ⋅⋅⋅in βi1′i1 ei1′ ⊗ β i2′ i2 ei2′ ⊗ = βi1′i1 β i2′ i2
n n 12 n 1
⊗ β in′ in ein′
2
βi′ i Ti i ⋅⋅⋅i ei′ ⊗ ei′ ⊗
⊗ ein′
⊗ ein′
= Ti1′i2′ ⋅⋅⋅in′ ei1′ ⊗ ei2′ ⊗
注:1.对于一个给定的张量,其各分量必须满足式(2.19)的转换 关系;否则,不能视为一个张量。 2.虽然张量的分量是随坐标系的变化而变化的,但张量的本身 则不随坐标系的变化而变化。 3.在一个给定的坐标系,若某一张量的所有分量都为零,则由 式(2.19)可知,在任意的坐标系中这一张量的所有分量也 必为零。这种张量称为零张量,用O表示。
a1 a2 = b1 c1 b2 c2 a3 b3 c3
(2.9)
设: a = ai ei
eijk和δij之间的关系及其证明 :
若i、j、k三个指标中有两个取相同的值,则显然 (2.10) 式(2.10)两边都为零值;或l、m、n中有两个 取相同的值,上式两边也同样为零。下面证明: 当指标i、j、k取三个不同的值,且同时l、m、n 由式(2.10)等号右端行列式的 也取三个不同的值时,式(2.10)是否成立。 分析可知,任意两行或两列较 如: 换一次,行列式的绝对值不 变,仅改变符号,且其符号改 变规则与置换符号的定义是相 (b) 符合的。
12 n
12 n
(2.19)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 2 章 二阶张量
研究定义在一个固定点(张量的元素是实常数, gi 也是常数)上的二阶张量随坐标系转动的
不同形式,不涉及与另一个张量的关系,也不涉及张量运动。
2.1 二阶张量的元素
T = Tij g i g j = Ti• j g i g j = T•ii gi g j = T ij gi g j
k n
(2) T 的不变量由无限多个(不变量的组合仍是不变量),通常关心的有两组:
主不变量( T 特征多项式的三个系数)
2
η1 = T•11 + T•22 + T•33 = G : T = T•mm = GmnT mn = GmnTmn = Tm•m
( )( ) η2
=
T•11 T•21
T•12 T•22
、 Ni• j
=
N•ji
,
(而一般: N•i j
≠
N
j •i
、
N
• i
j
≠
N •i j
在相同的,混变分量的转置 ≠ 系数矩阵的转置)
N ⋅u=u⋅N
(4) 反对称张量 Ω = −ΩT
性质: Ωij
=
−Ω 、 Ω ij ji
=
−Ω
ji
Ω 、 i •j
=
Ω − Ω 、 •i
•j
j
i
=
−Ω•ij ,
(而一般:
+ T•22 T•32
T•23 T•33
+ T•11 T•31
T•13 T•33
=
1 2
⎣⎡
G :T
G :T − T ⋅⋅T ⎦⎤
=
1 2
⎡⎣T•mmT•nn
− T•pqT•qp ⎤⎦
=
1 2
δ
ijpqT•jiT•qp
[共有 6 项相加,前后指标一样为正,不一样为负;指标 m, n 和 p, q 可以互换但乘积不
矩:
η1∗ = G : T = trT
η
∗ 2
=
T
⋅ ⋅T
=
tr(T
⋅T)=Fra bibliotekT•i
jT•
j i
( ) η3∗ = tr T ⋅ T ⋅ T
=
T•i
jT•
j k
T•ki
两者之间的关系:
( ) ( ) η1∗
=
η1
,η
∗ 2
=
η1
2
− 2η2 ,η3∗
= 3η3
+
η1
3
− 3η1η2
(3) 二阶张量的独立不变量有 6 个,对称二阶张量有 3 个,反对称张量 1 个。
变,所以要乘 1/2]
T•11 T•12 T•13
η3 = T•21
T•22
T•23
=
1 3!
εMT
⊗T
⊗TMε
=
1 6
δ limjknT•l iT•mjT•nk
=
1 6
ε
ijk ε lmnT•l iT•mjT•nk
T•31 T•32 T•33
[共有 6 项相加,前后指标均为顺序或逆序为正,一正一逆为负,有非序为零; l, m, n 均顺 序和均逆序的排列有 6 种,同样 i, j, k 也有六种,组合共有 36 种,除去重复的只有 6 种, 所以要乘 1/6]
同一坐标系下不同的并矢下,其分量也不同: Tij ≠ Ti• j ≠ T•ii ≠ T ij 。
(2) 定义转置张量:
( ) ( ) ( ) ( ) TT =
TT
gig j =
ij
TT
•j i
gi g j
=
TT
i •i
gi g j
=
TT
ij
gi g j
= Tji gi g j
=
T•
j i
gi
g
j
=
T
(4) [T ⋅ a,b,c] = [a,T ⋅ b,c] = [a,b,T ⋅ c] =η1 [a,b,c] [T ⋅ a,T ⋅ b,c] = [a,T ⋅ b,T ⋅ c] = [a,T ⋅ b,T ⋅ c] =η2 [a,b,c]
张量分量的数值随坐标改变而变化,但其某些组合却是不随坐标变化的标量---不变量。
(1) T 通过与自身 T 、 G 、 ε 进行缩并,得到的标量就是不变量:
G
:T
=
G ⋅⋅T
=
δ
jiT
j i
=
T
i i
T
⋅ ⋅T
=
T
ijT
j i
=
tr(T
⋅T )
εMT
⊗T
⊗T
Mε
=
εε ijk
T lmn
ilT
mj T
i =1
i =1
i =1
定理:[T ⋅ u, T ⋅ v, T ⋅ w] = detT [u, v, w]
[ det T 为两个平行六面体的体积比,三维空间中 3 个矢量是否线性相关取决与它们的混合积
是否为零] 正则与退化
det T ≠ 0 的二阶张量-正则二阶张量;否则为退化的二阶张量
(1) T 为正则 ⇔ u(i) (i=1,2,3) 性无关,则T ⋅ u(i) 也线性无关。
(2) 正则T 是单射的: u ≠ v ⇒ T ⋅ u ≠ T ⋅ v (3) 正则T 是满射的: ∀u 所作的线性变换T ⋅ u = v ,必存在唯一的逆变换T −1 ⋅ v = u 定义:正则二阶张量T ,必存在唯一的正则二阶张量T −1 使:T ⋅T −1 = T −1 ⋅T = G
2.3 二阶张量的不变量
= Ti•k
Gkj
=
g
Ti• k
⎤ ⎦
1
(6) 二阶张量的缩并(求迹): trT = T•ii ,
tr(T + S ) = T•ii + S•ii , tr(T ⋅ S ) = T ⋅ ⋅S , tr (T ⋅ ST ) = T : S
(7) 二阶张量与矢量的点积就是线性变换:
w =T ⋅u,
wi
•i j
gi
g
j
=T
ji gi g j
协、逆变分量指标交换,混变分量互相交换
= Tij g j gi
= Ti• j g j gi
=
Ti •i
g
j
gi
= T ij g j gi
也可以分量不动,并矢交换
(3) 对称张量 N = N T
性质: Nij
=
N ji 、 N ij
=
N
ji 、 N•i j
=
N
•i j
Ωi •j
≠
−Ω•ij 、 −Ωi • j
=
−Ωj•i
在相同的
(5) 行列式的值:
定义: detT = T•i j , Tij = g Ti• j = T•i j g = g 2 T ij , g = Gij
`Tij
= Tij
、 `T ij
= T ij
、 `Ti • j
=
T•
j i
、
⎡ ⎣
Tij
= Ti•k Gkj
= Ti′j′ g i′ g j′
= Ti′• j′ g i′ g j′
=
T i′ • i′
gi′
g
j′
= T i′j′ gi′ g j′
同一坐标系 另一坐标系
(1) 不同坐标系中实体不变,但其分量不同: Tij ≠ Ti′j′,
T•j i
≠
T• i′
j′
,
Ti •j
≠
T ,i′ • j′
T ij ≠ T i′j′
=
T
i j
⋅uj
,T
⋅u
≠
u⋅T
但 T ⋅u ≠ u⋅TT
2.2 正则与退化的二阶张量
定理:任意二阶张量将一个线性相关的矢量集映射为线性相关的矢量集
【设矢量集 u(i) 线性相关,则存在不全为零的实数α(i) 使:
I
I
I
∑α (i)u(i) = 0 , 0 = T ⋅ ∑α (i)u(i) = ∑α(i) (T ⋅ u(i)) , 所以T ⋅ u(i) 也线性相关】
研究定义在一个固定点(张量的元素是实常数, gi 也是常数)上的二阶张量随坐标系转动的
不同形式,不涉及与另一个张量的关系,也不涉及张量运动。
2.1 二阶张量的元素
T = Tij g i g j = Ti• j g i g j = T•ii gi g j = T ij gi g j
k n
(2) T 的不变量由无限多个(不变量的组合仍是不变量),通常关心的有两组:
主不变量( T 特征多项式的三个系数)
2
η1 = T•11 + T•22 + T•33 = G : T = T•mm = GmnT mn = GmnTmn = Tm•m
( )( ) η2
=
T•11 T•21
T•12 T•22
、 Ni• j
=
N•ji
,
(而一般: N•i j
≠
N
j •i
、
N
• i
j
≠
N •i j
在相同的,混变分量的转置 ≠ 系数矩阵的转置)
N ⋅u=u⋅N
(4) 反对称张量 Ω = −ΩT
性质: Ωij
=
−Ω 、 Ω ij ji
=
−Ω
ji
Ω 、 i •j
=
Ω − Ω 、 •i
•j
j
i
=
−Ω•ij ,
(而一般:
+ T•22 T•32
T•23 T•33
+ T•11 T•31
T•13 T•33
=
1 2
⎣⎡
G :T
G :T − T ⋅⋅T ⎦⎤
=
1 2
⎡⎣T•mmT•nn
− T•pqT•qp ⎤⎦
=
1 2
δ
ijpqT•jiT•qp
[共有 6 项相加,前后指标一样为正,不一样为负;指标 m, n 和 p, q 可以互换但乘积不
矩:
η1∗ = G : T = trT
η
∗ 2
=
T
⋅ ⋅T
=
tr(T
⋅T)=Fra bibliotekT•i
jT•
j i
( ) η3∗ = tr T ⋅ T ⋅ T
=
T•i
jT•
j k
T•ki
两者之间的关系:
( ) ( ) η1∗
=
η1
,η
∗ 2
=
η1
2
− 2η2 ,η3∗
= 3η3
+
η1
3
− 3η1η2
(3) 二阶张量的独立不变量有 6 个,对称二阶张量有 3 个,反对称张量 1 个。
变,所以要乘 1/2]
T•11 T•12 T•13
η3 = T•21
T•22
T•23
=
1 3!
εMT
⊗T
⊗TMε
=
1 6
δ limjknT•l iT•mjT•nk
=
1 6
ε
ijk ε lmnT•l iT•mjT•nk
T•31 T•32 T•33
[共有 6 项相加,前后指标均为顺序或逆序为正,一正一逆为负,有非序为零; l, m, n 均顺 序和均逆序的排列有 6 种,同样 i, j, k 也有六种,组合共有 36 种,除去重复的只有 6 种, 所以要乘 1/6]
同一坐标系下不同的并矢下,其分量也不同: Tij ≠ Ti• j ≠ T•ii ≠ T ij 。
(2) 定义转置张量:
( ) ( ) ( ) ( ) TT =
TT
gig j =
ij
TT
•j i
gi g j
=
TT
i •i
gi g j
=
TT
ij
gi g j
= Tji gi g j
=
T•
j i
gi
g
j
=
T
(4) [T ⋅ a,b,c] = [a,T ⋅ b,c] = [a,b,T ⋅ c] =η1 [a,b,c] [T ⋅ a,T ⋅ b,c] = [a,T ⋅ b,T ⋅ c] = [a,T ⋅ b,T ⋅ c] =η2 [a,b,c]
张量分量的数值随坐标改变而变化,但其某些组合却是不随坐标变化的标量---不变量。
(1) T 通过与自身 T 、 G 、 ε 进行缩并,得到的标量就是不变量:
G
:T
=
G ⋅⋅T
=
δ
jiT
j i
=
T
i i
T
⋅ ⋅T
=
T
ijT
j i
=
tr(T
⋅T )
εMT
⊗T
⊗T
Mε
=
εε ijk
T lmn
ilT
mj T
i =1
i =1
i =1
定理:[T ⋅ u, T ⋅ v, T ⋅ w] = detT [u, v, w]
[ det T 为两个平行六面体的体积比,三维空间中 3 个矢量是否线性相关取决与它们的混合积
是否为零] 正则与退化
det T ≠ 0 的二阶张量-正则二阶张量;否则为退化的二阶张量
(1) T 为正则 ⇔ u(i) (i=1,2,3) 性无关,则T ⋅ u(i) 也线性无关。
(2) 正则T 是单射的: u ≠ v ⇒ T ⋅ u ≠ T ⋅ v (3) 正则T 是满射的: ∀u 所作的线性变换T ⋅ u = v ,必存在唯一的逆变换T −1 ⋅ v = u 定义:正则二阶张量T ,必存在唯一的正则二阶张量T −1 使:T ⋅T −1 = T −1 ⋅T = G
2.3 二阶张量的不变量
= Ti•k
Gkj
=
g
Ti• k
⎤ ⎦
1
(6) 二阶张量的缩并(求迹): trT = T•ii ,
tr(T + S ) = T•ii + S•ii , tr(T ⋅ S ) = T ⋅ ⋅S , tr (T ⋅ ST ) = T : S
(7) 二阶张量与矢量的点积就是线性变换:
w =T ⋅u,
wi
•i j
gi
g
j
=T
ji gi g j
协、逆变分量指标交换,混变分量互相交换
= Tij g j gi
= Ti• j g j gi
=
Ti •i
g
j
gi
= T ij g j gi
也可以分量不动,并矢交换
(3) 对称张量 N = N T
性质: Nij
=
N ji 、 N ij
=
N
ji 、 N•i j
=
N
•i j
Ωi •j
≠
−Ω•ij 、 −Ωi • j
=
−Ωj•i
在相同的
(5) 行列式的值:
定义: detT = T•i j , Tij = g Ti• j = T•i j g = g 2 T ij , g = Gij
`Tij
= Tij
、 `T ij
= T ij
、 `Ti • j
=
T•
j i
、
⎡ ⎣
Tij
= Ti•k Gkj
= Ti′j′ g i′ g j′
= Ti′• j′ g i′ g j′
=
T i′ • i′
gi′
g
j′
= T i′j′ gi′ g j′
同一坐标系 另一坐标系
(1) 不同坐标系中实体不变,但其分量不同: Tij ≠ Ti′j′,
T•j i
≠
T• i′
j′
,
Ti •j
≠
T ,i′ • j′
T ij ≠ T i′j′
=
T
i j
⋅uj
,T
⋅u
≠
u⋅T
但 T ⋅u ≠ u⋅TT
2.2 正则与退化的二阶张量
定理:任意二阶张量将一个线性相关的矢量集映射为线性相关的矢量集
【设矢量集 u(i) 线性相关,则存在不全为零的实数α(i) 使:
I
I
I
∑α (i)u(i) = 0 , 0 = T ⋅ ∑α (i)u(i) = ∑α(i) (T ⋅ u(i)) , 所以T ⋅ u(i) 也线性相关】
