13简明材料力学习题答案第十三章
第十三章北航 材料力学 全部课件 习题答案
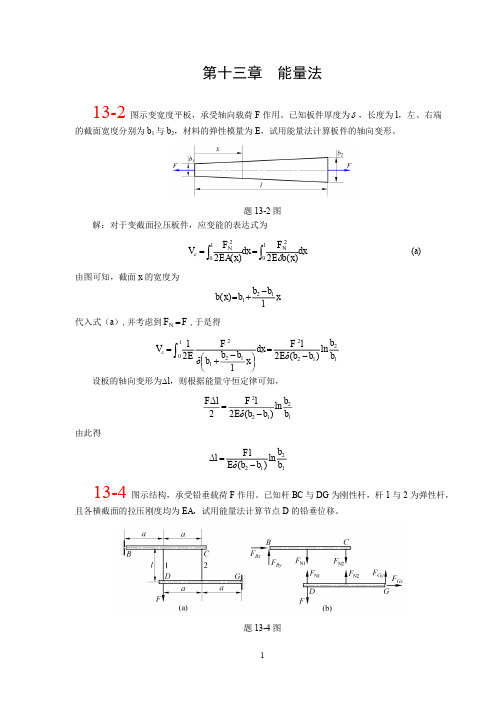
M ( x2 ) Fx2 M C ,
图 13-9 根据卡氏定理,得
C
1 [ EI
a 0
( Fx1 )(
x1 )dx1 a
a 0
( Fx2 )(1)dx2 ]
5Fa 2 () 6EI
A A
13-10 图示各梁,弯曲刚度 EI 均为常数,试用卡氏定理计算横截面 A 的挠度 与转角 。
3 3
3 3
–F
F 2
3 Fa 3 3 Fa 12
3 Fa 12
3
a
3 6
9
故有
ΔB
求 AB 的运算过程列表如下: i 1 2 3
i 1
3
F Ni FNi li 3Fa (←) EA 12EA
li
a a a
F Ni
2 3a 1
FNi
F
F Ni FNi l i
2 3 F 3
3a 1
–F
3 F 3
3 F 6
3a
F 2
故有
5 3 F 6
AB
F Ni FNi li 5 3F () EA 6 EA i1
3
(b) 解:求Δ B 和 AB 的单位状态分别示如图 13-17b(1)和 b(2) 。
图 13-17b 求 Δ B 的运算过程列表如下:
i 1 2 3 4
转角。
图示刚架,承受载荷 F 作用。设弯曲刚度 EI 为常数,试用卡氏定理计算截面 C 的
题 13-9 图 解:在截面 C 处假想附加一矩为 M C 的力偶(见图 13-9) ,由图可得
M x1 ( F
材料力学课后习题答案13章

= 7.44 × 10− 2 m = 74.4mm
而
2 × 0.050 Fd = (300 N ) 1 1 + + 2.22 × 10 − 2
= 1.004 × 10 3 N
M max = 1.004 ×10 3 N (1.00m ) = 1.004 ×10 3 N ⋅ m
设压杆微弯平衡时的挠曲轴方程为
πx w = f sin l
式中,f 为压杆中点的挠度即最大挠度。
题 13-8 图 解:由题设可知,
w = f sin
πx , l
6
w′ =
πf πx cos l l
据此可得
λ (x ) =
q cr 所作之功为
1 x 2 * 1 ( w′) dx = 2 0 2
∫
∫
x 0
(也可通过左侧题号书签直接查找题目与解)
13-2
比为 8:3。
图示圆截面简支梁,直径为 d,承受均布载荷 q 作用,弹性模量 E 与切变模量 G 之
(1)若同时考虑弯矩与剪力的作用,试计算梁的最大挠度与最大转角; (2)当 l/d =10 与 l/d =5 时,试计算剪切变形在总变形(最大挠度与最大转角)中所占百分比。
(2)被冲击面(弹簧顶面)的静位移为
∆st =
最大冲击载荷为
Pl P 500 + = 1.516 × 10 − 5 m + m = 2.52 × 10 − 3 m 3 EI k 200 × 10
2h + + Fd = P 1 1 ∆ st
于是,杆内横截面上最大的正应力为
Fl 3 ∆= 48EI
得刚度系数
0.030 4 48 × 200 × 10 × F 48 EI 12 N = 6.48 × 10 5 N k= = 3 = 3 ∆ m m l 1.00
材料力学习题册答案-第13章 能量法

5.如下图刚架受一对平衡力F作用,各段的EI相同且等于常量,试用图乘法求两端A、B间的相对转角。
解:应用图乘法,在A、B点加一对单位力偶。它们的内力图如下图。
6.图示刚架,各段的抗弯刚度均为EI。试计算B截面的水平位移和C截面的转角。
解:应用图乘法,在B截面加一水平单位力,在C截面加一单位力偶,它们的内力图如下图。
第十三章能量法
一、选择题
1.一圆轴在图1所示两种受扭情况下,其〔A〕。
A应变能相同,自由端扭转角不同;
B应变能不同,自由端扭转角相同;
C应变能和自由端扭转角均相同;
D应变能和自由端扭转角均不同。
〔图1〕
2.图2所示悬臂梁,当单独作用力F时,截面B的转角为θ,假设先加力偶M,后加F,那么在加F的过程中,力偶M〔C〕。
A不做功;B做正功;
C做负功,其值为 ;D做负功,其值为 。
3.图2所示悬臂梁,加载次序有下述三种方式:第一种为F、M同时按比例施加;第二种为先加F,后加M;第三种为先加M,后加F。在线弹性范围内,它们的变形能应为〔D〕。
A第一种大;B第二种大;
C第三种大;D一样大。
4.图3所示等截面直杆,受一对大小相等,方向相反的力F作用。假设杆的拉压刚度为EA,材料的泊松比为μ,那么由功的互等定理可知,该杆的轴向变形为 ,l为杆件长度。〔提示:在杆的轴向施加另一组拉力F。〕
A 0;B ;
C ;D无法确定。
〔图2〕〔图3〕
二、计算题
1.图示静定桁架,各杆的拉压刚度均为EA相等。试求节点C的水平位移。
解:解法1-功能原理,因为要求的水平位移与P力方向一致,所以可以用这种方法。
由静力学知识可简单地求出各杆的内力,如下表所示。
材料力学(金忠谋)第六版答案第14章

材料力学(金忠谋)第六版答案第14章第十三章 动载荷13-1 铸铁杆AB 长m l 8.1=,以等角速度绕垂直轴O -O 旋转如图示。
已知铸铁的比重3/74m kN =γ,许用拉应力[]MPa 40=σ,材料的弹性模量E =160 Gpa 。
试求此杆的极限转速,并计算此杆在转速m r n /100=时的绝对伸长。
解: (1) 极限转速m rn s s l g l g A A Ndl gA dr r qd r Nd x r gAdr ma r qd x r a jx dl n n 1092260137.114175.130799.010*******.92)2(][2][)2(21][)2(21)()()()()(235222222222====⨯⨯⨯⨯⨯=≤≤≤======⎰πωωγσωσωγσσωγωγω(2) 当n =1000m rcm m Eg l r EA r Nd l s n l 0252.01052.28.91016039.072.104107423)2(2)(2172.1046010002602492233220=⨯=⨯⨯⨯⨯⨯⨯⨯===∆=⨯==-⎰ωππω(2)吊索: MPa A P d d 55.2105276.14max=⨯==-σ13-3 轴上装一钢质圆盘,盘上有一圆孔。
若轴与盘以s140=ω的匀角速度旋转,论求轴内由这一圆孔引起的最大正应力。
解:23max max 22225.1212.021*********.01060041411060064003.03.047800640404.0mMN W M mN L P N Na gA ma P s m r a z d d d d n n d n =⨯⨯==⋅=⨯⋅===⨯⨯⨯⨯=⋅⋅⋅===⨯==πσπδγω13-4 飞轮轮缘的平均直径D =1.2m ,材料比重3/72m kN =γ,弹性模量GPa E 200=,轮缘与轮幅装配时的过盈量mmD2.0=∆,若不计轮相的影响,求飞轮允许的最大转速。
简明材料力学习题解答

简明材料力学习题解答标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]3-1. 用截面法求图示各杆在截面1-1、2-2、3-3上的扭矩。
并于截面上有矢量表示扭矩,指出扭矩的符号。
作出各杆扭矩图。
解: (a)(1) 用截面法求1-1截面上的扭矩(2) 用截面法求2-2(3) 画扭矩图(b)(1) 用截面法求1-1截面上的扭矩(2) 用截面法求2-2截面上的扭矩(21 x2xT xx(3) 用截面法求3-3截面上的扭矩(4) 画扭矩图. 直径D =50 mm处的切应力,并求横截面上的最大切应力。
解: (1) 圆轴的极惯性矩点的切应力(2) 圆轴的抗扭截面系数截面上的最大切应力注:截面上的切应力成线性分布,所以也可以用比例关系求最大切应力。
. 发电量为1500 kW 的水轮机主轴如图示。
D =550 mm ,d =300 mm ,正常转速n =250r/min 。
材料的许用剪应力[τ]=500 MPa 。
试校核水轮机主轴的强度。
解:(1) 计算外力偶矩(2) 计算扭矩(3) (4) 强度校核T强度足够。
注:强度校核类问题,最后必需给出结论。
3-5. 图示轴AB 的转速n =120 r/min ,从B 轮输入功率P = kW ,功率的一半通过锥形齿轮传送给轴C ,另一半由水平轴H 输出。
已知D 1=60 cm ,D 2=24 cm ,d 1=10 cm ,d 2=8 cm ,d 3=6 cm ,[τ]=20 MPa 。
试对各轴进行强度校核。
解:(1(2(3)计算抗扭截面系数(4)强度校核强度足够。
3-6. 图示阶梯形圆轴直径分别为d 1=40 mm ,d 2=70 mm ,轴上装有三个带轮。
已知由轮3输入的功率为P 3=30 kW ,轮1输出的功率为P 1=13 kW ,轴作匀速转动,转速n =200 r/min ,许用扭转角[θ]=2 o /m 。
试校核轴的强度和刚度。
解:(1) 计算外力偶矩 (2) 计算扭矩T(3) 计算抗扭截面系数(4) 强度校核强度足够。
工程力学材料力学(北京科大东北大学版)第4版13章习题答案

第一章参考答案1-1: 解:(a):N 1=0,N 2=N 3=P (b):N 1=N 2=2kN (c):N 1=P,N 2=2P,N 3= -P (d):N 1=-2P,N 2=P (e):N 1= -50N,N 2= -90N (f):N 1=0.896P,N 2=-0.732P 注(轴向拉伸为正,压缩为负)1-2: 解: σ1= 2118504P kN S d π==35.3Mpa σ2=2228504P kNS d π==30.4MPa∴σmax =35.3Mpa 1-3:解:下端螺孔截面:σ1=19020.065*0.045P S ==15.4Mpa上端单螺孔截面:σ2=2PS =8.72MPa上端双螺孔截面:σ3= 3PS =9.15Mpa∴σmax =15.4Mpa 1-4:解: 受力分析得: F 1*sin15=F 2*sin45 F 1*cos15=P+F 2*sin45∴σAB = 11F S =-47.7MPa σBC =22F S =103.5 MPa1-5:解: F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2FS =38.1MPa1-6:解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm (2) ∴AB l ∆=-0.02mm 1-7:解:AC AC AC LNL EA EA σε===1.59*104, CB CB CB LNL EA EA σε===6.36*1041-8:解: 1-9:解: 1-10:解:[][]max 59.5MPa σσ=<1-11:解:(1)当45oα=,[]11.2σσ=>强度不够(2)当60oα=,[]9.17σσ=< 强度够1-12:解:1-13:解:[]max 200213MPa MPa σ=< 1-14:解: 1.78, 1.26d cm d cm==拉杆链环1-15 解:22BC F Q ==70.7 kN查表得: 45*45*3 1-16解:(1)[]2401601.5ssn σσ===MPa(2)1-17 解:(1)'61544014.521542390F n F ===≈1-18 解:P=119kN 1-19 解:所以最大载荷 84kN 1-20 解: P=33.3 kN 1-21 解: 1-22 解: 1-23 解:第二章习题2-1 一螺栓连接如图所示,已知P=200 kN , =2 cm ,螺栓材料的许用切应力[τ]=80Mpa ,试求螺栓的直径。
大学物理13章习题详细答案
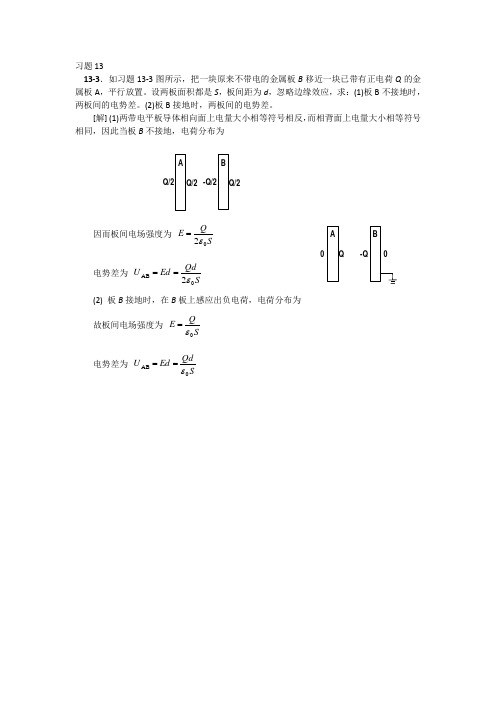
习题1313-3.如习题13-3图所示,把一块原来不带电的金属板B 移近一块已带有正电荷Q 的金属板A ,平行放置。
设两板面积都是S ,板间距为d ,忽略边缘效应,求:(1)板B 不接地时,两板间的电势差。
(2)板B 接地时,两板间的电势差。
[解] (1)两带电平板导体相向面上电量大小相等符号相反,而相背面上电量大小相等符号相同,因此当板B 不接地,电荷分布为因而板间电场强度为 SQ E 02ε=电势差为 SQdEd U 0AB 2ε== (2) 板B 接地时,在B 板上感应出负电荷,电荷分布为 故板间电场强度为 SQ E 0ε=电势差为 SQdEd U 0AB ε== B A-Q/2Q/2Q/2Q/2A B -QQ13-4 两块靠近的平行金属板间原为真空。
使两板分别带上面电荷密度为0的等量异号电荷,这时两板间电压为U 0=300V 。
保持两板上电量不变,将板间空间一半如图习题13-4图所示充以相对电容率为r =5的电介质,试求(1) 金属板间有电介质部分和无电介质部分的E,D 和板上的自由电荷密度; (2) 金属板间电压变为多少电介质上下表面束缚电荷面密度多大13-5.如习题13-5图所示,三个无限长的同轴导体圆柱面A 、B 和C ,半径分别为R A 、R B 、R C 。
圆柱面B 上带电荷,A 和C 都接地。
求B 的内表面上线电荷密度1和外表面上线电荷密度2之比值1/2。
[解] 由A 、C 接地 BC BA U U = 由高斯定理知 r E 01I 2πελ-=rE 02II 2πελ= AB 0101I BA ln 2d 2d ABA BR Rr r U R R R R πελπελ=-==⎰⎰r E IIIB C 0202II BC ln 2d 2d CB CBR R r r U R R R R πελπελ===⎰⎰r EBC 02A B 01ln 2ln 2R R R R πελπελ= 因此 AB BC 21ln :ln:R R R R =λλ13-6.如习题13-6图所示,一厚度为d 的无限大均匀带电导体板,单位面积上两表面带电量之和为。
揭示材料力学的奥秘知到章节答案智慧树2023年山东农业工程学院

揭示材料力学的奥秘知到章节测试答案智慧树2023年最新山东农业工程学院第一章测试1.从材料力学的角度来讲,为了使构件能正常的工作,必须使构件具有足够的()。
参考答案:其余选项都是2.材料力学研究的内力是构件各部分的相互作用力。
()参考答案:错3.因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
()参考答案:错4.材料力学只限于研究弹性范围内的小变形情况。
()参考答案:对5.角应变是变形后,构件中任意两根微线段夹角角度的变化量。
()参考答案:错第二章测试1.在下列说法中,正确的是()。
参考答案:内力随外力的增大而增大2.用截面法求内力时,是对()建立平衡方程而求解的。
参考答案:左段或右段3.关于轴向拉压杆件轴力的说法中,错误的是()。
参考答案:轴力是沿杆轴作用的外力4.计算M-M面上的轴力。
()参考答案:-P5.梁在某一段内作用有向下的分布载荷时,在该段内它的弯矩图为( )参考答案:上凸曲线第三章测试1.拉杆伸长后,横向会缩短,这是因为杆有横向应力存在。
()参考答案:错2.虎克定律适用于弹性变形范围内。
()参考答案:错3.材料的延伸率与试件的尺寸有关。
()参考答案:对4.应用拉压正应力公式的条件是()。
参考答案:外力的合力沿杆轴线;5.一圆截面直杆,两端受的拉力相同,若将长度增大一倍其他条件不变,则下列结论错误的是( )。
参考答案:伸长量不变第四章测试1.挤压发生在局部表面,是连接件在接触面上的相互压紧;而压缩是发生在杆件的内部。
()参考答案:对2.剪断钢板时,所用外力使钢板产生的应力大于材料的屈服极限。
()参考答案:错3.在平板与螺栓之间加一垫片,可以提高()的强度。
参考答案:平板挤压4.在冲床上将钢板冲出直径为d的圆孔,冲力F与()。
参考答案:与直径d成正比5.对于圆柱形连接件的挤压强度问题,应该直接用受挤压的半圆柱面来计算挤压应力。
()参考答案:错第五章测试1.圆杆受扭时,杆内各点均处于纯剪切状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:方法1:
两杆的变形
外力的功
功能原理
方法2:
两杆的内力
变形能
13.2.图示杵架各杆的材料相同截面面积相等,在P力作用下,试求桁架的变形能。
解:(1)求约束力
(2)分析铰B
(3)分析铰D
(4)分析铰C
(5)桁架的变形能
解:(1)约束反力
(2)弯矩方程
(3)在C处作用单位集中力
截面C的挠度
(4)在B处作用单位集中力偶
截面B的转角
顺时针转向
13.9.试求图示各梁截面B的挠度和转角。EI=常量
解:(1)在B处作用虚加力Pf和Mf,并列出弯矩方程
(2)上式分别对Pf和Mf求偏导数
(3)用卡氏定理求挠度和转角
(4)令上两式中的Pf和Mf为零
解:(1)写出曲杆的弯矩方程
(2)在B处垂直方向作用单位集中力
B的垂直位移
(3)在B处水平方向作用单位集中力
B的水平位移
13.28.图示折轴杆的横截面为圆形,在力偶矩m作用下,试求自由端的线位移和角位移。
解:(1)求水平杆的扭矩方程和垂直杆的弯矩方程
(2)在自由端分别单独作用一单位力和单位力偶,并求出相应的扭矩方程和弯矩方程
解:(1)由于结构和载荷对称,取刚架一半分析
(2)弯矩方程
(3)应用卡氏定理
(4)A、B间的相对位移
A、B两点相互靠近。
13.16.图示桁架各杆的材料相,截面面积相等,在载荷P作用下,试求节点B与D间的相对位移。
解:(1)在B处作用虚加力Pf,并求出约束反力
(2)求各杆的轴力
(3)上式分别对Pf求偏导数
(2)弯矩方程和扭矩方程
(3)变形能
(4)使用功能原理求解本题
13.6.试用互等定理求跨度中点C的挠度,设EI=常量。
解:(a)
(1)将P力移到C截面处,如下图
(2)由位移互等定理
方向向上
(b)
(1)将P力移到C截面处,如下图
(2)由位移互等定理
方向向下
13.8.车床主轴可简化成EI=常量的当量轴,如图所示,试求在载荷P作用下,截面C的挠度和前轴承B处的截面转角。
(3)用卡氏定理求C点垂直位移
方向向下。
13.23.平面刚架如图所示。刚架各部分截面相同,试求截面A的转角。
解:(1)求各杆的弯矩方程
(2)在梁上A处单独作用一单位力偶源自并列出弯矩方程(3)用莫尔定理求A截面的转角
转角的方向与单位力偶方向相同。
13.25.等截面曲杆BC的轴线为四分之三的圆周,如图所示。若AB可视为刚性杆,在P作用下,试求截面B的水平位移及垂直位移。
(4)用卡氏定理求B点沿BD方向的位移
(5)令上式中的Pf为零
方向为B向D靠近
13.20.图示简易吊车的撑杆AC长为2m,截面的惯性矩I=8.53×106mm4。拉杆BD的A=600mm2。P=2.83kN。如撑杆只考虑弯曲影响,试求C点的垂直位移,设E=200GPa。
解:(1)求出约束反力
(2)求BD杆的轴力和AC杆的弯矩
(3)用莫尔定理求C端的垂直位移
自由端的垂直位移单位力方向一致。
13.3.平均半径为R的细圆环,截面为直径为d的圆形。两个力P垂直于圆环轴线所在的平面(见图)。试求两个力P作用点的相对位移。
解:(1)求曲杆的扭矩方程和弯矩方程
(2)上两式分别对P求偏导数
(3)用卡氏定理求垂直位移
13.23.图示杆系各杆的材料相同,截面面积相等。试用力法求各杆的内力。
解:(1)属一次静不定问题,取C为多余约束,约束反力为X1
列出用力法求解的基本方程
(2)求1P
由上图知
分别对D点受力分析
由莫尔定理
(3)求δ11
(4)求出X1
(5)求杆的内力
2杆受拉,3杆受压。
挠度和转角的方向与虚加力的方向一致
13.9.图示刚架各杆的的EI相等。试求A的位移和截面C的转角。
解:(a)应用莫尔定理
(1)刚架各段的弯矩方程
(2)在A处垂直方向作用单位集中力
A的垂直位移
(3)在A处水平方向作用单位集中力
A的水平位移
(4) 在C处作用单位集中力偶
C截面的转角
顺时针转向
13.18.图示刚架各部分的EI相等,在一对P力作用下,求A、B两点间的相对位移。
13.3.计算图示各杆的变形能。
解:(b)
方法1:
(1)查表得C截面的转角
(2)由功能原理
方法2
(1)列出梁的弯矩方程
(2)求弯曲变形能
(c)
(1)列出梁的弯矩方程
(2)求弯曲变形能
13.4.传动轴受力情况如图所示,轴直径为40 mm,E=210 GPa,G=80 GPa。试计算轴的变形能。
解:(1)传动轴受力
(3)用莫尔定理求自由端的位移
自由端的线位移和角位移和方向与单位力和单位力偶方向一致。
13.26.图示曲拐的自由端C上作用集中力P。曲拐两段材料的相同,且均为同一直径的圆截面杆,试求C点的垂直位移。
解:(1)求BC杆的弯矩方程及AB杆的扭矩方程和弯矩方程
(2)在C端单独作用一单位力,并求出相应的扭矩方程和弯矩方程
