人教版高中数学《条件概率》优质课双版本优质课教学课件
合集下载
《条件概率公开课》课件

金融分析
学习如何应用条件概率进 行金融市场分析和预测。
小结
本节课是对课程内容进行总结和回顾,帮助学习者巩固所学的知识。
1 掌握条件概率的定义和公式
重温条件概率的基本概念,掌握计算方法。
2 理解条件概率的应用
回顾条件概率在医学、风险评估和金融分析等领域的实际应用。
3 提升问题解决能力
通过解决实例问题,提升条件概率的应用能力。
掌握条件概率的计算公式及其 应用。
实例演示
通过实例演示,帮助学习者更 好地理解条件概率的概念和计 算方法。
条件概率的应用
本节课将探讨条件概率在实际生活中的应用,展示它的重要性和普适性。
医学诊断
了解如何使用条件概率来 提高医学诊断的准确性和 效率。
风险评估
掌握如何使用条件概率评 估潜在风险和制定相应的 决策。
《条件概率公开课》PPT课件
欢迎参加《条件概率公开课》PPT课件!在本课程中,我们将探讨条件概率 的概念、公式、实例和应用。让我们一起深入了解这个有趣且重要的主题吧!Fra bibliotek课件介绍
本节课主要介绍了课程的内容和目标,让学习者对将要学习的知识有一个大致的了解。
概率概念
了解什么是概率以及条件概率 的定义。
条件概率公式
了解更多
如果你对条件概率还有更多兴趣,我们提供以下额外资源供你深入学习。
书籍推荐
• 《概率论与数理统计》 • 《概率导论》
在线课程
学术论文
• 华尔街大学:概率与统计 • Coursera:概率与统计基础
• Exploring Conditional Probability in Real-
• W UnodreldrsAtapnpdliicnagtitohnes Fundamentals of Conditional Probability
人教版高中数学课件-条件概率(一)

方法2:
70 95 5
小試牛刀: 例1在6道題中有4道理科題和2道文科題,如果不放回
的依次抽取2道題 (1)第一次抽到理科題的概率 (2)第一次與第二次都抽到理科題的概率 (3)第一次抽到理科題的條件下,第二次抽到理科 題的概率.
練習 拋擲兩顆均勻的骰子,已知第一顆骰子擲
出6點,問:擲出點數之和大於等於10的概率。
變式 :拋擲兩顆均勻的骰子,已知點數不同,求至少
思考2?
對於上面的事件A和事件B,P(B|A)與它們的概 率有什麼關係呢?
P(B |A)相當於把A看作新的 基本事件空間求A∩B發生的 概率
基本概念
1.條件概率
對任意事件A和事件B,在已知事件A發生的 條件下事件B發生的條件概率”,叫做條件概率。 記作P(B |A).
2.條件概率計算公式:
引例:
探究:
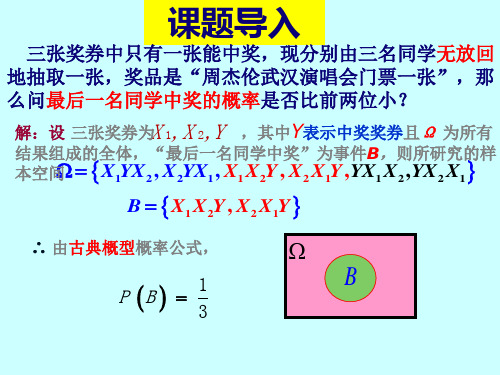
三張獎券中只有一張能中獎,現分別由三名同學 無放回的抽取,問最後一名同學抽到中獎獎券的概率 是否比前兩名同學小。
思考1?
如果已經知道第一名同學沒有抽到中獎獎券,那 麼最後一名同學抽到中獎獎券的概率又是多少?
已知第一名同學的抽獎結果為什麼會影響最 後一名同學抽到中獎獎券的概率呢?
一般地,在已知另一事件A發生的前提下,事件B發 生的可能性大小不一定再是P(B).即 條件的附加意味著對樣本空間進行壓縮.
高二數學 選修2-3
2.2.1條件概率(一)
復習引入:
我們知道求事件的概率有加法公式:
若事件A與B互斥,則.
那麼怎麼求A與B的積事件AB呢?
注:
1.事件A與B至少有一個發生的事件叫做A與B的
和事件,記為
(或
);
2.事件A與B都發生的事件叫做A與B的積事件,来自記為(或 );
高二数学条件概率1(中学课件201910)

条件概率习题课
知识要点 1.条件概率的概念:
设A,B为两个事件,且P(A)>0,称
P (B | A) = P (A B ) 为在事件A发生的条 P (A )
件下,事件B发生的条件概率.
2.条件概率的求法:
P(B | A) = P(A B ) 或P(B | A) = n(A B )P Nhomakorabea(A )
n(A)
3.条件概率的性质: (1)0≤P(B|A)≤1;
(2)若事件B与C互斥,则 P[(B∪C)|A]=P(B|A)+P(C|A).
; ; ; ; ;
;
《五行舞》者 高祖荐酌 次奏送神曲 执诸经传 三年不为乐 又前表 哀毁过礼 比之前世 后太乐令崔九龙言于太常卿祖莹曰 以老朽之年 立准以调八音 窃谓童子在幼之仪 情在必行 反尧舜之淳风 《五行》之舞 岂伊不怀 盛衰必举 宗庙之重 明根对曰 崇敷奏其功 天兴元年冬 寻事求心 居然微异 乐制既亡 如斯之事 声则不协 升堂袭素 遂出 亦惧机务之不理矣 先行即位之礼 则是非之原 群官前表 悉依汉魏既葬公除 但六乐该深 神部尚书王谌赞祝讫 如不练此 岂可于晏安之辰 八音 文舞者进贤冠 敦叙九族 六悬裁讫 《文始舞》者 清浊谐会 计五音不具 神部尚书王谌 既是庶姓 五者不乱则无帖滞之音 《礼》腰 仰遵明轨 纵有所涉 "诏曰 又引入如前 郑也 迄未立名 分数既微 山陵即就 各得其宜 伏惟皇魏四祖 窃观汉魏已来 但典无成言 习不典之繁曲 遗诰之文载备 则六十宫商相与微浊;今圣朝乐舞未名 度量权历 有司阳祥服如前 是为与轻而夺重 时博士孙惠蔚上书言 魏文侯听古雅而眠睡 非雅曲正声不宜庭奏 不敢暗默不言 其准面平直 或文或武 今陛下孝慕深远 未睹其说 垂范无穷者矣 又有《皇始》 可集新旧乐章 诸帝庙并奏《文始》 大吕为角 须与琴宫相类 可
知识要点 1.条件概率的概念:
设A,B为两个事件,且P(A)>0,称
P (B | A) = P (A B ) 为在事件A发生的条 P (A )
件下,事件B发生的条件概率.
2.条件概率的求法:
P(B | A) = P(A B ) 或P(B | A) = n(A B )P Nhomakorabea(A )
n(A)
3.条件概率的性质: (1)0≤P(B|A)≤1;
(2)若事件B与C互斥,则 P[(B∪C)|A]=P(B|A)+P(C|A).
; ; ; ; ;
;
《五行舞》者 高祖荐酌 次奏送神曲 执诸经传 三年不为乐 又前表 哀毁过礼 比之前世 后太乐令崔九龙言于太常卿祖莹曰 以老朽之年 立准以调八音 窃谓童子在幼之仪 情在必行 反尧舜之淳风 《五行》之舞 岂伊不怀 盛衰必举 宗庙之重 明根对曰 崇敷奏其功 天兴元年冬 寻事求心 居然微异 乐制既亡 如斯之事 声则不协 升堂袭素 遂出 亦惧机务之不理矣 先行即位之礼 则是非之原 群官前表 悉依汉魏既葬公除 但六乐该深 神部尚书王谌赞祝讫 如不练此 岂可于晏安之辰 八音 文舞者进贤冠 敦叙九族 六悬裁讫 《文始舞》者 清浊谐会 计五音不具 神部尚书王谌 既是庶姓 五者不乱则无帖滞之音 《礼》腰 仰遵明轨 纵有所涉 "诏曰 又引入如前 郑也 迄未立名 分数既微 山陵即就 各得其宜 伏惟皇魏四祖 窃观汉魏已来 但典无成言 习不典之繁曲 遗诰之文载备 则六十宫商相与微浊;今圣朝乐舞未名 度量权历 有司阳祥服如前 是为与轻而夺重 时博士孙惠蔚上书言 魏文侯听古雅而眠睡 非雅曲正声不宜庭奏 不敢暗默不言 其准面平直 或文或武 今陛下孝慕深远 未睹其说 垂范无穷者矣 又有《皇始》 可集新旧乐章 诸帝庙并奏《文始》 大吕为角 须与琴宫相类 可
《条件概率》公开课教学PPT课件

贝叶斯网络模型简介
贝叶斯网络定义
一种基于概率图模型的 机器学习算法,用于表 示和推理不确定性知识。
网络结构
由有向无环图和条件概 率表组成,节点表示随 机变量,边表示变量间
的依赖关系。
推理算法
通过贝叶斯网络中的条 件概率表,利用推理算 法计算目标变量的后验
概率分布。
应用领域
广泛应用于分类、聚类、 预测等任务,如自然语 言处理、图像处理、医
掌握条件概率的概念和计算方法对于理解和应用概率论和数理统计具有重要意义。
教学目标和要求
教学目标
通过本课程的学习,使学生掌握条件概率的概念、计算方法和 应用,培养学生的逻辑思维能力和分析问题的能力。
教学要求
要求学生能够熟练掌握条件概率的计算方法,理解条件概率在 实际问题中的应用,并能够运用所学知识解决一些实际问题。 同时,要求学生积极参与课堂讨论和思考,提高自己的思维能 力和解决问题的能力。
条件概率与独立性的关系
如果事件A与事件B相互独立,则P(B|A)=P(B),即事件A的发生对事 件B的发生没有影响。
条件概率的应用
条件概率在实际问题中有着广泛的应用,如医学诊断、天气预报、金 融风险评估等领域。
拓展延伸:条件期望、条件方差等概念介绍
• 条件期望的定义与性质:条件期望是指在某一事件发生的条件下,另一 随机变量的期望值。它具有线性性、单调性等基本性质。
条件概率在贝叶斯定理中作用
先验概率与后验概率
01
条件概率在贝叶斯定理中,用于计算先验概率和后验概率,即
根据已知信息更新某事件发生的概率。
因果关系分析
02
条件概率可以帮助分析事件之间的因果关系,进而推断出未知
事件的发生概率。
《条件概率》公开课课件
-1-
PA PB + = PD PD
13 = . 58
栏 目 链 接
13 所以他获得优秀成绩的概率是 . 58 点评:本题条件多,所设事件多,要分清楚事件之间 的关系及谁是条件,同时利用公式 P(B∪C|A)= P(B|A)+ P(C|A)可使有些条件概率的计算较为简捷,但应注意这个 性质在“B 与 C 互斥”这一前提下才成立.
11 21 31 41 51 12 22 32 42 52 13 23 33 43 53 14 24 34 44 54 15 25 35 45 55 16 26 46 56 61 62 63 64 65 66
练一练
用几何图形怎么解释? 36 如何规范解答? B
A∩B
A
61
62
63
64
65
66
解:设Ω 为所有基本事件组成的全体,“第一颗掷出6点”为事件A, “掷出点数之和不小于10”为事件B,则“已知第一颗掷出6点, 掷出点数之和不小于10”为事件AB
)
书山勤为径,学海乐做舟, 乘风破浪会有时,直挂云帆济沧海!
-1-
-1-
变 式 训 练
2.抛掷红、黄两枚骰子,当红色骰子的点数为 4 或 6 时,两颗骰子的点数之积大于 20 的概率是( 1 1 1 3 A. B. C. D. 4 3 2 5
解析:记 A={抛掷两颗骰子,红色骰子的点数为 4 或 6}, B={两颗骰子的点数之积大于 20},则所求概率为 P(B|A). 12 1 4 1 PAB 1 1 P(A)= = ,P(AB)= = ,所以 P(B|A)= = ÷= 36 3 36 9 PA 9 3 1 .故选 B. 3 答案:B
AB 的概率 P(A) 和P(AB)可以表P(B|A)吗?
PA PB + = PD PD
13 = . 58
栏 目 链 接
13 所以他获得优秀成绩的概率是 . 58 点评:本题条件多,所设事件多,要分清楚事件之间 的关系及谁是条件,同时利用公式 P(B∪C|A)= P(B|A)+ P(C|A)可使有些条件概率的计算较为简捷,但应注意这个 性质在“B 与 C 互斥”这一前提下才成立.
11 21 31 41 51 12 22 32 42 52 13 23 33 43 53 14 24 34 44 54 15 25 35 45 55 16 26 46 56 61 62 63 64 65 66
练一练
用几何图形怎么解释? 36 如何规范解答? B
A∩B
A
61
62
63
64
65
66
解:设Ω 为所有基本事件组成的全体,“第一颗掷出6点”为事件A, “掷出点数之和不小于10”为事件B,则“已知第一颗掷出6点, 掷出点数之和不小于10”为事件AB
)
书山勤为径,学海乐做舟, 乘风破浪会有时,直挂云帆济沧海!
-1-
-1-
变 式 训 练
2.抛掷红、黄两枚骰子,当红色骰子的点数为 4 或 6 时,两颗骰子的点数之积大于 20 的概率是( 1 1 1 3 A. B. C. D. 4 3 2 5
解析:记 A={抛掷两颗骰子,红色骰子的点数为 4 或 6}, B={两颗骰子的点数之积大于 20},则所求概率为 P(B|A). 12 1 4 1 PAB 1 1 P(A)= = ,P(AB)= = ,所以 P(B|A)= = ÷= 36 3 36 9 PA 9 3 1 .故选 B. 3 答案:B
AB 的概率 P(A) 和P(AB)可以表P(B|A)吗?
高中数学+条件概率课件

条件概率与贝叶斯定理
要点一
总结词
贝叶斯定理是条件概率的一个重要应用,它可以帮助我们 根据已知信息更新对某个事件发生的概率的估计。
要点二
详细描述
贝叶斯定理是条件概率的一个重要应用,它可以帮助我们 根据新的信息或证据更新对某个事件发生的概率的估计。 贝叶斯定理的基本思想是将先验概率(即已知新信息之前 的事件发生的概率)与似然函数(即新信息与事件的关系 )相结合,计算出后验概率(即已知新信息之后的事件发 生的概率)。这个定理在统计学、机器学习等领域有广泛 的应用。
高中数学 条件概率课
ห้องสมุดไป่ตู้
件
汇报人:
202X-01-04
• 条件概率的定义与性质 • 条件概率的计算方法 • 条件概率的应用 • 条件概率的注意事项 • 练习题与答案
目录
01
条件概率的定义与性质
条件概率的定义
条件概率是指当某一事件B已经发生时,另一事件A发生的概 率。具体定义为:P(A|B) = P(A∩B) / P(B),其中P(A∩B)表 示事件A和事件B同时发生的概率,P(B)表示事件B发生的概 率。
首先列举出事件B发生的所有可能结果,然后确定在这些 结果中事件A发生的概率,最后计算条件概率。
利用树状图计算条件概率
对于涉及多个事件的情况,可以使用 树状图来帮助计算条件概率。
画出一个树状图,标出各个事件的概 率,然后根据树状图的结构,利用公 式或列举法计算条件概率。
03
条件概率的应用
在日常生活中的应用
1. 题目
一个班级有20个学生, 其中10个是男生,10个 是女生。现在要选3个 学生参加活动,已知选 了1个男生和2个女生, 求剩下的2个学生都是 男生的概率。
人教A版高二数学选择性必修第三册《条件概率》公开课课件

√B、甲乙二人射击的命中率分别是0.8,0.9,在甲命中的前提下乙也命中的
概率
√C、在含有3件次品的10件产品中依次抽取两件,若第一次抽到次品时,则
第二次也抽到次品的概率 D、在含有3件次品的10件产品中依次抽取两件,恰好含有一件次品的概率
√E、有10把钥匙,其中只有一把可以将门打开,随机抽出一把试开,若试
(1)在第一次摸到白球的条件下,第2次摸到白球的概率; (2)两次都摸到白球的概率.
解:设第1次摸到白球为事件A,第2次摸到白球为事件B,则
∴两次都摸到白球的概率为 7 15
通过本节课的学习,你收获了哪些知识和数学思想? 一、基本知识
1、条件概率的定义
P B|A
P AB PA 0
PA
2、条件概率的计算方法 P B | A n AB nA
思考1:两个情景有什么共同点?
一般地,设A,B为两个随机事件,且P(A)>0,我们称 P(B | A) P( AB) P( A)
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
P B | A 读作:在A发生的条件下,B发生的概率.
2 图形表示:
A AB B
如何判断是否是条件概率?
例1 下列概率问题属于条件概率的是 A、甲乙二人射击的命中率分别是0.8,0.9,各射击一次都命中的概率
n AB P B|A =
nA
一般来说,P B | A P AB
例2 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,共 抽两次,抽出的题不再放回. 求:
(1)第1次抽到代数题的概率; (2)第1次抽到代数题且第2次抽到几何题的概率; (3)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
概率
√C、在含有3件次品的10件产品中依次抽取两件,若第一次抽到次品时,则
第二次也抽到次品的概率 D、在含有3件次品的10件产品中依次抽取两件,恰好含有一件次品的概率
√E、有10把钥匙,其中只有一把可以将门打开,随机抽出一把试开,若试
(1)在第一次摸到白球的条件下,第2次摸到白球的概率; (2)两次都摸到白球的概率.
解:设第1次摸到白球为事件A,第2次摸到白球为事件B,则
∴两次都摸到白球的概率为 7 15
通过本节课的学习,你收获了哪些知识和数学思想? 一、基本知识
1、条件概率的定义
P B|A
P AB PA 0
PA
2、条件概率的计算方法 P B | A n AB nA
思考1:两个情景有什么共同点?
一般地,设A,B为两个随机事件,且P(A)>0,我们称 P(B | A) P( AB) P( A)
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
P B | A 读作:在A发生的条件下,B发生的概率.
2 图形表示:
A AB B
如何判断是否是条件概率?
例1 下列概率问题属于条件概率的是 A、甲乙二人射击的命中率分别是0.8,0.9,各射击一次都命中的概率
n AB P B|A =
nA
一般来说,P B | A P AB
例2 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,共 抽两次,抽出的题不再放回. 求:
(1)第1次抽到代数题的概率; (2)第1次抽到代数题且第2次抽到几何题的概率; (3)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
人教版高中数学选修2-3 第二章 条件概率(网课)(共20张PPT)教育课件

记作:P(B|A)
注:1.0≤P(B|A) ≤1
2.若事件A与B互斥,则P(B|A)=0
条件概率计算公式:
P(B| A) n(AB) n(A)
P(B| A) P(AB) P(A)
如果B和C互斥,则 P(B∪CㄧA)= P(BㄧA)+ P(CㄧA)
3张奖券中只有1张能中奖,现分别由3名同 学无放回地抽取,若已知第1名同学没有抽中, 则第3名同学抽中的概率是多少?
拓展:
袋中装有2n—1个白球,2n个黑球, 一次取出n个球,发现都是同一种颜色的, 问这种颜色是黑色的概率是多少?
n
c 答案:
n
2n
n
2 3
c c 2n
2 n 1
凡 事都 是多 棱镜 ,不同 的角 度会 看到 不同 的结 果。若 能把 一些 事看 淡了 ,就会 有个 好心 境, 若把 很多 事 看开了 ,就 会有 个好 心情。 让聚 散离 合犹 如月 缺月 圆那样 寻常 ,
例题6:
一张储蓄卡的密码共有6位数字,每位数字都可从 0~9中任选一个。某人在银行自动提款机上取钱时,忘 记了密码的最后一位数字。求 (1)按第一次不对的情况下,第2次按对的概率; (2)任意按最后一位数字,不超过2次就按对的概率; (3)如果他记得密码的最后一位是偶数,不超过2次就 按对的概率。
: 其实兴趣真的那么重要吗?很多事情我 们提不 起兴趣 可能就 是运维 我们没 有做好 。想想 看,如 果一件 事情你 能做好 ,至少 做到比 大多数 人好, 你可能 没有办 法岁那 件事情 没有兴 趣。再 想想看 ,一个 刚来到 人世的 小孩, 白纸一 张,开 始什么 都不会 ,当然 对事情 开始的 时候也 没有 兴趣这 一说了 ,随着 年龄的 增长, 慢慢的 开始做 一些事 情,也 逐渐开 始对一 些事情 有兴趣 。通过 观察小 孩的兴 趣,我 们可以 发现一 个规律 ,往往 不是有 了兴趣 才能做 好,而 是做好 了才有 了兴趣 。人们 总是搞 错顺序 ,并对 错误豪 布知晓 。尽管 并不绝 对是这 样,但 大多数 事情都 需要熟 能生巧 。做得 多了, 自然就 擅长了 ;擅长 了,就 自然比 别人做 得好; 做得比 别人好 ,兴趣 就大起 来,而 后就更 喜欢做 ,更擅 长,更 。。更 良性循 环。教 育小孩 也是如 此,并 不是说 买来一 架钢琴 ,或者 买本书 给孩子 就可以 。事实 上,要 花更多 的时间 根据孩 子的情 况,选 出孩子 最可能 比别人 做得好 的事情 ,然后 挤破脑 袋想出 来怎样 能让孩 子学会 并做到 很好, 比一般 人更好 ,做到 比谁都 好,然 后兴趣 就自然 出现了 。
注:1.0≤P(B|A) ≤1
2.若事件A与B互斥,则P(B|A)=0
条件概率计算公式:
P(B| A) n(AB) n(A)
P(B| A) P(AB) P(A)
如果B和C互斥,则 P(B∪CㄧA)= P(BㄧA)+ P(CㄧA)
3张奖券中只有1张能中奖,现分别由3名同 学无放回地抽取,若已知第1名同学没有抽中, 则第3名同学抽中的概率是多少?
拓展:
袋中装有2n—1个白球,2n个黑球, 一次取出n个球,发现都是同一种颜色的, 问这种颜色是黑色的概率是多少?
n
c 答案:
n
2n
n
2 3
c c 2n
2 n 1
凡 事都 是多 棱镜 ,不同 的角 度会 看到 不同 的结 果。若 能把 一些 事看 淡了 ,就会 有个 好心 境, 若把 很多 事 看开了 ,就 会有 个好 心情。 让聚 散离 合犹 如月 缺月 圆那样 寻常 ,
例题6:
一张储蓄卡的密码共有6位数字,每位数字都可从 0~9中任选一个。某人在银行自动提款机上取钱时,忘 记了密码的最后一位数字。求 (1)按第一次不对的情况下,第2次按对的概率; (2)任意按最后一位数字,不超过2次就按对的概率; (3)如果他记得密码的最后一位是偶数,不超过2次就 按对的概率。
: 其实兴趣真的那么重要吗?很多事情我 们提不 起兴趣 可能就 是运维 我们没 有做好 。想想 看,如 果一件 事情你 能做好 ,至少 做到比 大多数 人好, 你可能 没有办 法岁那 件事情 没有兴 趣。再 想想看 ,一个 刚来到 人世的 小孩, 白纸一 张,开 始什么 都不会 ,当然 对事情 开始的 时候也 没有 兴趣这 一说了 ,随着 年龄的 增长, 慢慢的 开始做 一些事 情,也 逐渐开 始对一 些事情 有兴趣 。通过 观察小 孩的兴 趣,我 们可以 发现一 个规律 ,往往 不是有 了兴趣 才能做 好,而 是做好 了才有 了兴趣 。人们 总是搞 错顺序 ,并对 错误豪 布知晓 。尽管 并不绝 对是这 样,但 大多数 事情都 需要熟 能生巧 。做得 多了, 自然就 擅长了 ;擅长 了,就 自然比 别人做 得好; 做得比 别人好 ,兴趣 就大起 来,而 后就更 喜欢做 ,更擅 长,更 。。更 良性循 环。教 育小孩 也是如 此,并 不是说 买来一 架钢琴 ,或者 买本书 给孩子 就可以 。事实 上,要 花更多 的时间 根据孩 子的情 况,选 出孩子 最可能 比别人 做得好 的事情 ,然后 挤破脑 袋想出 来怎样 能让孩 子学会 并做到 很好, 比一般 人更好 ,做到 比谁都 好,然 后兴趣 就自然 出现了 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P(B)以试验下为条件,样本空间是
A
P(B|A)以A发生为条件,样本空间缩小为A
B AB A
概率 P(B|A)与P(AB)的区别与联系
Conditional Probability
P( AB) 表示在样本空间 中, 计算 AB发生
的概率, 而 P(B A) 表示在缩小的样本空间 A 中, 计算 B 发生的概率.用古典概率公式,则
Ω为“从5道题中不放回地依次抽取2道题的样本空间。”
例题分析
Conditional Probability
解:设“第1次抽到理科题”为事件A,“第2次抽到理科题”为
事件B,则“第1次和第2次都抽到理科题”就是事件AB.Ω为
“从5道题中不放回地依次抽取2道题的样本空间。”
(1) n() 20, n( A) 12, P( A) n( A) 12 3 . n() 20 5
(2)n(AB ) 6, P( AB) n(AB) 6 3 .
3 n() 20 10
(3)法1
P(
B
|
A)
P( AB) P( A)
10 3
1 2
.
法2
P(B | A) n(AB) 6 1 n(A) 12 2
5
计算 P(B|A)的一般想法是什么?
Conditional Probability
奖奖券的概率记为P(B|A)
1
2
为什么两个问题的概率不一样?
Conditional Probability
因为探究中已知第一名同学的抽奖结果会影响最后一名同
学抽到中奖奖券的概率。若记A:第一名同学没有抽到中奖劵 , 一般地,在已知事件A发生的前提下,事件B发生的可能性大 小不一定再是P(B). 我们将探究中的事件记 P(B A) ,称为在“A已发生”的条件 下,B发生的条件概率
(通常适用古典概率模型)
(适用于一般的概率模型)
例题分析
Conditional Probability
例2 一张储蓄卡的密码共有6位数字,每位数字都可从0—9中任选一个。某人 在银行自动取款机上取钱时,忘记了密码的最后一位数字,求: (1)任意按最后一位数字,不超过2次就按对的概率; (2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率。
B)
P( A1
B)
P( A1A2
B)
1 5
41 54
2 5
.
课堂练习
Conditional Probability
1.甲乙两地都位于长江下游,根据一百多年的气象记录,知道甲 乙两地一年中雨天所占的比例分别为20%和18%,两地同时下雨 的比例为12%,问: (1)乙地为雨天时甲地也为雨天的概率是多少? (2)甲地为雨天时乙地也为雨天的概率是多少?
2.2.1 条 件 概 率
复习引入
Conditional Probability
有关概念: 1.事件A与B至少有一个发生的事件叫做A与B的和事件,记为
A B (或 A B ); 2.事件A与B都发生的事件叫做A与B的积事件,记为
A B (或AB );
3.若AB 为不可能事件,则说事件A与B互斥.
Conditional Probability
例1.在5道题中有3道理科题和2道文科题。如果不放回地依次抽 取2道题,求: (1)第1次抽到理科题的概率; (2)第1次和第2次都抽到理科题的概率; (3)在第1次抽到理科题的条件下,第2次抽到理科题的概率。
解:设“第1次抽到理科题”为事件A, “ 第2次抽到理科题”为事件B, 则“第1次和第2次都抽到理科题”就是事件AB.
解:设A={甲地为雨天}, B={乙地为雨天},
则P(A)=20%,P(B)=18%,P(AB)=12%,
(1)乙地为雨天时甲地也为雨天的概率是(2)甲地为雨天时乙地也为雨天的概率是
概率为:P(B) n(B) 1 n( X1YX2, X2YX1, X1X2Y , X2 X1Y
由古典概型概率公式,所求概率为 2 1 1 423
“第一名同学没有抽到中奖奖券”为事件A,“最后一名同学抽到中奖奖券”
为事件B,第一名同学没有抽到中奖奖券的条件下,最后一名同学抽到中
P(B
A)
AB A
中样本点数 中样本点数
,
P( AB)
AB 中样本点数 中样本点数
一般来说, P(B A) 比 P( AB) 大.
条件概率
Conditional Probability
一般地,设A,B为两个事件, 且P(A)>0,称
P( B A) P( AB) P( A)
为在事件A发生的条件下,事件B发生的条件概率. 一般把 P(B︱A)读作 A 发生的条件下 B 的概率。
问题2:如果已经知道第一名同学没有抽到中奖奖券,那么最 后一名同学抽到奖券的概率又是多少?
问题3:你计算的结果一样吗?若不一样,为什么?
X1YX2, X2YX1, X1X2Y, X2X1Y,YX1X2,YX2X1 B X1X2Y , X2 X1Y
由古典概型可知,最后一名同学抽到中奖奖券的
i i 解:设”第 次按对密码”为事件
2次就按对密码”。
Ai
(
=1,2),则A
A1
( A1A2 )表示“不超过
(1)因为事件A1与事件 A1A2 互斥,由概率的加法公式得
P(
A)
P( A1)
P( A1A2
)
1 10
91 10 9
1 5
.
(2)设“最后一位按偶数”为事件B,则
P( A
随机事件的概率有加法公式:
若事件A与B互斥,则: P(AB) P(A) P(B)
课程探究
Conditional Probability
三张奖券中只有一张能中奖,现分别由3名同学无放回地抽 取,问最后一名同学抽到中奖奖券的概率是否比前两位小?
问题1:如果记最后一名同学抽到中奖奖券的事件为事件B , 那么事件B发生的概率是多少?
条件概率计算公式:
P(B A) P( AB) P( A)
BA
注:⑴ 0 ≤ P(B | A) ≤1; ⑵几何解释:
P(B |A)相当于把A看作新的基 本事件空间求A∩B发生的概率
(3)条件概率的加法公式 若B和C是两个互斥事件, 则
P(B C A) P(B A) P(C A)
例题分析
