截面法求内力解析
第二节截面法求内力
作业：
1、有一低碳钢杆件受三力如图，F1=30KN, F2=10KN, F3=20KN,求杆件各截面处的内力。
F1 A F2
B
C F3
2、试求图中所示各杆件横截面1-1、2-2、3-3上 的轴力。F1=50KN，F2=40KN，F3=30KN。
讨论： 图示阶梯杆AD受三个集中力F 作用，设AB、 BC、CD段的横截面面积分别为A、2A、 3A，则三段杆的横截面上（） （A）轴力不等，应力相等； （B）轴力相等，应力不等； （C）轴力和应力都相等； （D）轴力和应力都不等。
m
1、确定要截开的次 数和位置
2、任选取一段为研 究对象 3、假设出截面上的 内力 4、用平衡方程求出 截面上的内力
F A
m
F B FN F FN 选左段时：∑Fx=O －F+FN＝0 FN＝F 选右段时：∑Fx=O F－FN＝0 FN＝F
F
例1：试求图3—1所示杆件指定各截面上的内力大 小。 解：(1)计算截面1—1的内力.
截面法求内力
学习目标：
1、掌握“截面法”的定义； 2、正确理解和应用截面法求内力的一
般步骤；
一、什么是截面法？
截面法：将受外力作用的杆件假想地切
开，用以显示内力的大小，并以平衡条 件确定其合力的方法，称为截面法。它
是分析杆件内力的唯一方法。
如图AB杆受两个力，一个向左，一个向右， 大小均为F。作用点分别为A和B。
3 F1 A
2 F2
2 C
1
F3 1 D
3 B
FN3
F1
Hale Waihona Puke F2 （c）F3练习：求杆件各处的内力。
F１＝
2
1
F2＝
浅探内力分析之截面法
浅探内力分析之截面法摘要: 材料力学离不开内力分析，截面法更是求内力的一般方法，在展开工程设计时，如果建筑的受力分析准确性得不到保障，那么建筑的安全性和耐久性等就会出现问题。
本文从截面法对不同种内力的具体应用进行初步研究寻找其计算方法。
关键词: 材料力学；内力；截面法引言在工程设计过程中会运用许多的理论力学知识，截面法便是其中至关重要的一种，且短时间内难以被取代，因此截面法受到广泛运用。
本文即从截面法对不同种内力的具体应用题展开计算分析。
1 截面法1.1 截面法的定义截面法：用截面假想地把构件分成两部分，以此来分析明确内力大小，并以平衡条件确定其合力的方法。
1.2 截面法的研究对象内力：物体在受到外力作用而变形时,其内部各质点间的相对位置将发生变化。
相应地,各质点间的相互作用力也将发生改变。
这种由外力作用而引起的质点间相互作用力的改变量,即为材料力学中所研究的内力。
1.3 截面法的步骤主要分以下三个步骤：1、截开：在需要求内力的截面处，假想地将杆分为两部分；2、代替：将两部分中的任意一部分留下，把弃去部分对留下部分的作用，以作用在截面上的内力（力或力偶）代替；3、平衡：对留下部分建立平衡方程，根据上面的已知外力来计算杆件在截开面上的未知内力。
注意，截开面上的内力对留下部分而言已属外力。
图 12 轴力与杆件轴线相重合的内力，称为轴力，用符号FN表示。
轴力的正负规定: 当轴力的指向离开截面时,杆受拉,规定轴力为正;反之,当轴力指向截面时,杆受压,规定轴力为负。
即拉为正,压为负。
2.1 轴力分析计算已知F1=4OKN，F2=-30KN，求AB杆的内力。
应用截面法求杆件横截面上的内力，如图2所示。
截开：用假想平面m-m将构件切开分为两部分。
代替：取出其中任一部分如I部分为研究对象,画出I部分的受力图平衡：列出Ⅰ部分的平衡方程式:由∑Fx=0，得Fx-F=0，得FN=F1=4OKN（背离横截面,拉力为正）求BC杆的内力。
试述求杆件横截面上内力的截面法步骤和方法
试述求杆件横截面上内力的截面法步骤和方法1. 了解截面法哎，说到工程力学里的截面法，别让这些名字吓坏了，其实就是一种找出杆件内部力量的简单方法。
咱们平常接触的建筑物、桥梁，或者一些机械构件，都是通过这种方法来确保它们的稳固和安全的。
这个方法简单来说就是用“剪刀”切一刀，把杆件“分尸”，然后分析切面上受力的情况。
好比是咱们剥苹果皮，剥开之后看里面的果肉，这样能更清楚地了解苹果的质量。
2. 截面法的步骤2.1 选取截面首先，挑选一个合适的截面，瞅准了方向之后，就下手了。
这个步骤就像在你脑子里画出一条切割线。
你得选择一个合适的位置，把杆件从中间“切开”。
这里要注意，选取的位置一定要使得切面上的力易于计算。
如果这个位置选错了，结果就像你在黑暗中找钥匙一样，费劲不讨好。
2.2 画出受力图接下来，别忘了给这片“切面”画上图。
要把杆件切开后，分离出的部分的受力情况画出来。
图上得标明各种内力，比如剪力、轴力和弯矩等等。
这些力就像是在打游戏时，你需要记录你的角色的状态和装备一样，你要准确记录这些力的情况，这样才能确保你计算的准确。
2.3 列出平衡方程然后，你就要写平衡方程了。
平衡方程是用来保证杆件在切开时的受力状态是平衡的，不会乱七八糟。
这些方程包括了力的平衡、力矩的平衡等。
就像你玩积木，如果要保持积木塔不倒，就得仔细计算每一块积木的放置位置。
2.4 解方程找内力最后，你要解这些方程，找出杆件内部的力量。
就像做数学题一样，把方程算出来，你就能得到具体的内力数值。
这个步骤可不能马虎，不然得到的结果就像是空话，没有实际意义。
3. 截面法的应用3.1 结构分析截面法在结构分析中的应用非常广泛。
无论是大桥、小楼，还是家里的门框，都是用这个方法来确保结构的安全性。
就像是大厨做菜，得先知道每种材料的用量和比例，才能做出美味的菜肴。
工程师用截面法就像是这个大厨，通过计算内力，确保建筑的稳定性和安全性。
3.2 机械设计在机械设计中，截面法也是必不可少的。
第二章 杆件的内力·截面法讲解
F
FN （＋）FN
F
F
FN （－）FN
F
轴力图： 轴力沿轴线变化的图形
F
F
FN
轴力图的意义
+ x
① 直观反映轴力与截面位置变化关系； ② 确定出最大轴力的数值及其所在位置，即确定危险截面位置，为 强度计算提供依据。
例 图示杆的A、B、C、D点分别作用着大小为FA = 5 F、 FB = 8 F、 FC = 4 F、 FD= F 的力，方向如图，试求各段内力并画出杆 的轴力图。
应变
一、正应变（线应变）定义
av
Du Ds
棱边 ka 的平均正应变
lim
Du k点沿棱边 ka 方向的正应变
Ds0 Ds
正应变特点
1、 正应变是无量纲量 2、 过同一点不同方位的正应变一般不同
二、切应变定义 微体相邻棱边所夹直角的
改变量 g ，称为切应变
切应变量纲与单位
切应变为无量纲量 切应变单位为 弧度（rad）
BC
D
FN 2 FB FC FD 0
FB
FC
FD
FN2= –3F，
求BC段内力：
FN3
C
D
Fx 0 FN3 FC FD 0 FN3= 5F，
FC
FD
FN4
D
求CD段内力：
Fx 0 FN 4 FD 0
FN4= F
FD
FN1 2F, FN2= –3F， FN3= 5F， FN4= F
M
M
取左段为研究对象：
M 0, T M 0 M x
Tx
T M
取右段为研究对象：
截面法是求杆件内力的基本方法
一、概述截面法是工程力学中用于求解杆件内力的基本方法之一。
在工程结构分析和设计中，了解截面法的原理和应用是至关重要的。
本文将深入探讨截面法的基本概念、原理和应用，以帮助读者更好地理解和应用这一方法。
二、截面法的基本概念1.1 概念简介截面法是工程力学中用于分析杆件内力的一种方法，它基于杆件内力平衡的原理，通过考察杆件的截面上的内力分布情况来求解杆件的内力。
1.2 截面法的基本原理截面法基于力的平衡原理，即在杆件的截面上，杆件的内力必须满足横向平衡和转矩平衡的条件。
通过分析截面上的内力分布情况，可以确定杆件内的弯矩、剪力和轴力。
1.3 截面法的应用范围截面法适用于各种杆件的内力分析，包括梁、柱、桁架等结构中的杆件。
在工程实践中，截面法常常用于分析结构内部的受力情况，为结构设计和分析提供重要依据。
三、截面法的具体步骤2.1 确定截面在应用截面法时，首先需要确定分析的截面位置。
通常情况下，选择距离受力部位较近的位置作为截面。
2.2 绘制内力图在截面上绘制出杆件内的剪力图和弯矩图，根据平衡条件和力学原理，确定内力的方向和大小。
2.3 计算内力根据绘制的剪力图和弯矩图，可以直接求解出截面上的剪力、弯矩和轴力大小。
这些内力是杆件在该截面上的受力情况的表示。
2.4 检验平衡通过检验内力图的平衡条件，验证所得的内力是否符合力学平衡定律。
如果内力满足平衡条件，则认为截面法计算是正确的。
四、截面法的应用举例3.1 梁的截面力分析以简支梁为例，说明如何利用截面法分析梁的内力情况。
根据距离支座较近的位置选择截面，绘制剪力图和弯矩图，并计算出截面上的内力情况。
3.2 柱的截面力分析以等截面柱为例，说明如何利用截面法分析柱的内力情况。
通过选择适当位置的截面，绘制出内力图，计算出截面上的轴力和弯矩。
五、截面法的优缺点4.1 优点截面法简单直观，易于理解和应用。
通过截面法可以直接得到截面上的内力分布情况，为结构的受力分析提供了重要依据。
02截面法求内力基本方法
ED杆内力如何求?
小结：
熟练掌握 计算桁架内力的基 本方法： 结点法和截面法
采取最简捷的途径计算桁架 内力
如何 计算？
FP
返 回 章
静定组合结构
特点 既有桁架杆，又有弯曲杆 一般有一些关键的联系杆
求解的关键点 选择恰当方法解决关键杆内力计算 选择截面时，必须注意区分两类杆
组合结构的计算
斜直 剪力图 水平线 线(
)
为 零 处
有突 变(突 变值=
FP)
如 变 号
无 无变化 影
响
一般 抛物 有 有尖 有 有突变
弯矩图 为斜 线(
极 角(向 极 （突变 为零
直线 下凸) 值 下） 值 值=M）
曲杆微分关系
曲杆微段
dFN ds
=-qt+
FQ R
dFQ ds
=qn-
FN R
dM ds
=FQ-m
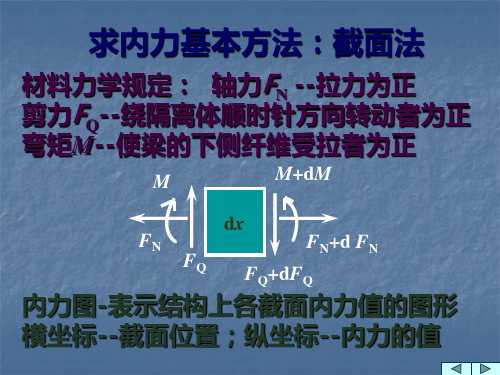
求内力基本方法：截面法
材料力学规定： 轴力FN --拉力为正 剪力FQ--绕隔离体顺时针方向转动者为正
弯矩M--使梁的下侧纤维受拉者为正
M
M+dM
dx
FN
dx
FN+d FN
FQ
FQ+dFQ
内力图-表示结构上各截面内力值的图形
横坐标--截面位置；纵坐标--内力的值
结构力学规定
正
MAB A端
FNAB
FQAB
一、根据维数分类 1. 平面（二维）桁架（plane truss） ——所有组成桁架的杆件以及荷载的作 用线都在同一平面内
2. 空间（三维）桁架（space truss） ——组成桁架的杆件不都在同一平面内
二、按外型分类 1. 平行弦桁架 2. 三角形桁架 3. 抛物线桁架 4. 梯形桁架
截面法求内力讲解
解： 1. 确定支座反力
B Fx 0 MA 0
FBy
Fy 0
FAx 0 2FPa FPa FBy 3a 0 FAy FBy 2FP 0
FBy
FP 3
FAy
5FP 3
2FP FQE
A 5FP
C E ME
3
Fy 0
2FP
FQE
5FP 3
0
C
a
FAy
b l
FPb l
+
FP a
-
l FQ图
FPab M图
l
B FBy
A FPb
l
FQ
M
MA 0
Fy 0
FBy
FP a l
FAy
FPb l
FQ
FQ
FPb l
(0 x a)
M
M FPb x (0 x a)
l
B
FQ
FP a l
(a x l)
FPa M FPa (l x)
平: 对留下部分写平衡方程求出内力的值
FQ(+)
FQ(+)
M(+)
M(+)
（1）平衡方程的正负和内力的正负是完全不同性质的两套符号系统。 （2）取简单部分作为隔离体，列平衡方程时，尽量使一个方程含有一个未知量
例1 求E截面内力
A FAx
FAy
2FP FPa
C
D
1.5a E
a
a
a
2. 用截面法研究内力
M JK J
F QJK
M JK J
简述截面法求内力的步骤
截面法求内力的步骤简介截面法是一种用于计算结构内力的方法，广泛应用于工程领域。
它通过将结构切割成若干个截面，分析每个截面上的受力情况，从而确定结构中各个部分的内力分布。
本文将详细介绍截面法求内力的步骤，包括确定切割截面、计算受力平衡、绘制剪力图和弯矩图等内容。
步骤一：确定切割截面在进行截面法计算之前，首先需要确定切割截面的位置。
通常情况下，选择合适的切割截面位置可以简化计算，并且使得结果更加准确。
切割截面的位置应该选择在结构受力变化较大或者存在集中荷载作用的地方。
步骤二：计算受力平衡在确定了切割截面之后，需要对每个切割截面进行受力平衡计算。
根据静力平衡原理，对于一个处于静止状态的结构，在任意一个切割截面上受到的外部作用力和内部反作用力之和应该为零。
可以利用受力平衡方程来计算切割截面上的内力。
步骤三：绘制剪力图剪力是指结构中某一截面上的内力，它与截面上的受力平衡有关。
在截面法求解内力时，常常需要绘制剪力图。
剪力图是以结构轴线为横坐标，剪力值为纵坐标的图形表示。
绘制剪力图的步骤如下：1.选择合适的坐标系，通常选取结构轴线作为横坐标。
2.根据受力平衡计算出每个切割截面上的剪力值。
3.将计算得到的剪力值绘制在相应位置上。
4.连接各个点，即可得到完整的剪力图。
步骤四：绘制弯矩图弯矩是指结构中某一截面上的内力，它与截面上的受力平衡和几何形状有关。
在截面法求解内力时，常常需要绘制弯矩图。
弯矩图是以结构轴线为横坐标，弯矩值为纵坐标的图形表示。
绘制弯矩图的步骤如下：1.选择合适的坐标系，通常选取结构轴线作为横坐标。
2.根据受力平衡和几何形状计算出每个切割截面上的弯矩值。
3.将计算得到的弯矩值绘制在相应位置上。
4.连接各个点，即可得到完整的弯矩图。
步骤五：计算其他内力除了剪力和弯矩之外，还有其他一些常见的内力需要计算，如轴力、扭矩等。
根据受力平衡和结构几何形状，可以通过类似的方法计算出这些内力，并绘制相应的图形。
步骤六：分析结果在完成内力计算之后，需要对结果进行分析。
《截面法求内力》课件
截面法求内力的基本步骤
确定截面位置
根据结构的特点和受力情况，选择适 当的截面位置。
进行截面分析
对所选截面进行详细的分析，包括该 截面的受力状态、约束条件以及与周 围结构的相互作用关系等。
计算内力
截面法的优缺点
截面法的优点在于简单易懂，易于操作，适用于各种形状和尺寸的构件。然而，截面法也存在一些局限 性，如对于复杂结构和多跨连续梁的计算可能较为繁琐，需要借助其他分析方法。
截面法求内力的展望
截面法的进一步研究和改进
随着科技的发展和工程实践的深入，截面法的研究也在不断进步。未来可以进一步研究截 面法的精度和可靠性，提高其计算效率和准确性。同时，可以结合数值分析方法和其他现 代技术手段，对截面法进行改进和优化。
《截面法求内力》 ppt课件
contents
目录
• 截面法求内力概述 • 截面法求内力的基本原理 • 截面法求内力的具体操作 • 截面法求内力的实例解析 • 截面法求内力的注意事项与优化建议 • 总结与展望
01
CATALOGUE
截面法求内力概述
截面法求内力的定义
截面法求内力是指在结构分析中，通过在结构上选择适当的截面，并按照一定的 步骤和方法，计算出该截面所承受的内力（如轴力、剪力和弯矩等）的方法。
内力计算
计算内力时，应考虑所有可能的受力情况， 避免遗漏。
边界条件
正确处理结构的边界条件，如固定、自由、 简支等，对分析结果至关重要。
优化建议
简化模型
使用软件辅助
在保证分析精度的前提下，尽量简化模型 ，减少计算量。
利用专业软件进行内力分析，可以大大提 高计算效率和准确性。
机械基础——第二节截面法求内力讲述
三、梁弯曲时的内力
P
P P P
P P P
P
1、弯曲变形的概念
杆件在载荷作用下，其轴线由原来的直线弯曲成 曲线，这种变形称为弯曲。 以弯曲变形为主的杆件通常称为梁。
（一）平面弯曲
梁有一个纵向对称面。 当外力都作用在该纵向对称面内，弯曲也 发生在该对称面内，我们称之为平面弯曲。 我们可以用梁轴线的变形代表梁的弯曲。
1、扭矩的概念
扭转变形的杆往往称之为扭转轴 扭转轴的内力称为扭矩
2、扭矩可利用截面法、并建立平衡方程求得 M M x M T-M=0 →T=M
T
3、扭矩正负号的规定
确定扭矩方向的右手法则：
伸出右手，四指沿扭矩转动的 方向，大拇指即为扭矩的方向 离开截面扭矩为正， 指向截面扭矩为负。
_
指向截面
+
离开截面
用截面法求扭矩时，先按正向假设。
4、扭矩图
将扭转轴各个截面扭矩沿轴线方向分布情况 用图形表示。
Y
637N· m
＋
X
－
318N· m 795N· m
例3-2 图示为一传动轴，主动 轮B输入功率PB=60 kW，从动 轮A、C、D输出功率分别为 PA=28 kW，PC=20 kW， PD=12 kW。轴的转速n=500 r/min，试绘制轴的转矩图。
（二） 梁的基本类型
1、载荷的简化 # 集中力 # 均布载荷 # 集中力矩 正负号规定： 集中力和均布载荷与坐标轴同向为正、反向为负； 集中力矩逆时针为正、顺时针为负。
2、约束的简化
根据支座对梁在载荷平面内的约束情况，一般可
以简化为三种基本形式：
FX FY
FX FY
M
FY
固定铰支座
构件内力的求解用截面法。
构件内力的求解用截面法。
构件内力的求解是工程力学中的一个重要问题。
截面法是一种常见的求解构件内力的方法之一。
本文将详细介绍截面法的基本原理和具体应用。
截面法的基本原理是基于静力学平衡条件，即在任何一个截面上，作用在该截面上的剪力、弯矩和轴力之和等于零。
因此，对于任意一个构件，只要确定其受力状态，就可以通过截面法求解出其各个截面上的内力。
截面法的求解过程通常分为以下几步：1. 确定截面：根据受力情况，选择需要求解的截面。
2. 切割构件：将构件沿着所选截面切割成两个或多个部分，形成一个自由体和一个受力体。
3. 建立平衡方程：对自由体和受力体分别建立平衡方程，其中包括剪力平衡、弯矩平衡和轴力平衡等。
4. 求解内力：通过求解平衡方程，计算出所选截面上的剪力、弯矩和轴力等内力。
5. 绘制内力图：根据所求得的内力，绘制出相应的内力图，以便于分析和设计。
截面法的具体应用广泛，常见的应用包括：1. 梁的内力求解：对于梁受到的外力和支反力情况，可以通过截面法求解出其各个截面上的剪力、弯矩和轴力等内力，从而进行梁的设计和分析。
2. 框架结构的内力求解：对于框架结构，可以通过截面法求解出每个构件的内力，从而得到结构的整体受力情况，进行结构的设计和分析。
3. 桥梁结构的内力求解：对于桥梁结构，可以通过截面法求解出桥梁各个截面的内力，从而进行桥梁的设计和分析。
例如，可以确定桥梁的最大荷载能力和最大跨度等参数。
截面法是一种常见的求解构件内力的方法，其基本原理是基于静力学平衡条件，通过建立平衡方程，计算出所选截面上的剪力、弯矩和轴力等内力。
在工程实践中，截面法被广泛应用于梁、框架结构和桥梁等工程领域。
截面法求内力讲解
l
l
(a ? x ? l)
x A FAy
M0
C
B
a
l
b FBy
? MA ? 0
? Fy ? 0
FBy
?
?
M0 l
FAy
?
M0 l
M0 l
+
FQ图
M 0b l
M0a l
M图
A M0 l
FQ
M
FQ
FQ
?
M0 l
M M ? M0 x
l
(0 ? x ? a) (0 ? x ? a)
B
FQ
?
M0 l
(a ? x ? l)
FAy 70 +
A
A
4m
2m 2m
FBy
A
EC D 10 10 -
B 70
50 50
FQ
FQ图（单位kN）
M
F
EC D
B
q FQ FQ ? 70 ? 20x
M ? 70x ? 10x2
M
40 B
FQ ? ?10
50 M ? 160 ? 10x
(0 ? x ? 4) (0 ? x ? 4)
(4 ? x ? 6) (4 ? x ? 6)
100 120 100 122.5
M图（单位kN.m）
FQ M
FQ ? ?50 (6 ? x ? 8)
B 50 M ? 400 ? 50x (6 ? x ? 8)
叠加法
条件：结构线弹性、小变形
荷载叠加法： 当结构上同时作用有许多荷载
时，先分别作出各荷载单独作用 下的内力图，再将各个内力图的 竖标相叠加（代数和），便得到 各荷载共同作用下的内力图。
内力、截面法及应力的概念 建筑力学
建筑力学
3
二、 截面法
• 截面法是求内力的基本方法。要确定杆件某一截面上的内力，可以 假想地将杆件沿需求内力的截面截开，将杆分为两部分，并取其中一 部分作为研究对象。此时，截面上的内力被显示出来，并成为研究对 象上的外力，再由静力平衡条件求出此内力。这种求内力的方法，称 为面法可归纳为三个步骤： 1．截开 欲求某一截面上的内力时，沿该截面假想地把杆件分成两部分（图5-3a），任取一 部分作为研究对象。 2．代替 用作用于截面上的内力代替弃去部分对研究部分的作用（图5-3b）或（图5-3c）。 3．平衡
一点处的集度，杆件中某截面上任一点的应力一般有两个分量：正应 力和剪应力。
4.求内力的基本方法----截面法 步骤：截开；代替；平衡。
建筑力学
11
单位换算：
建筑力学
8
本章小结
建筑力学
9
本章讨论了材料力学的一些基本概念。 1．材料力学的研究对象
是由均匀、连续、各向同性的弹性体材料制成的杆件。 2．杆件的四种基本变形形式 （1）轴向拉伸或压缩 （2）剪切 （3）扭转 （4）弯曲
建筑力学
10
3.内力与应力的概念 内力是杆件在外力作用下，相连两部分之间的相互作用力。 工程上最常见的是计算杆件横截面上的内力。应力是内力在某
对研究部分建立平衡方程，从而确定截面上内力的大小和方向。图5-3
建筑力学
5
三、应力
建筑力学
6
构件的破坏不仅与内力大小有关，还与内力在构件截面上 的密集程度（简称集度）有关。通常将内力在一点处的集度 称为应力。用式子表示为：P称为E点处应力。
建筑力学
7
通常应力P与截面既不垂直也不相切。材料力学中总是将它分解为垂直 于截面和相切于截面两个分量。垂直于截面的应力分量称为正应力或法 向应力，用σ表示；相切于截面的应力分量称为剪应力或切向应力，用τ 表示。
静定结构的内力—截面法求静定平面桁架内力(建筑力学)
2、 截面法
对于联合桁架或复杂桁架，单纯应用结点法不能求出全部杆件的轴力，因 为总会遇到有三个未知轴力的结点而无法求解，此时要用截面法求解。即使在 简单桁架中，求指定杆的轴力用截面法也比较方便。
截面法所选取的隔离体包含两个或两个以上的结点，隔离体上的力系是一
个平面一般力系，可以建立三个平衡方程：
0
A
FP
FP I
C 1
0 2a
00
3a
D 4I
2.5FP
a
a
取截面I－I以左为隔离体：
FP
FP I
C
1 0 2a
52
0A
00
3a
1
D 4I
Fx 0， 2.5FP
a
a
FN 1 FN 4 Fx 3 Fx 2 0， FN 1 (2.75FP 0.75FP 0.5FP )
1.5FP (压)。
Fx 2 0.5FP ； Fx 3 0.75FP； FN 4 2.75FP。
结 论：
结点法和截面法是计算桁架的两种基本方法，各有其优缺点。 结点法：适用于求解桁架全部杆件的内力，但求指定杆件内力时，一般来说比较 繁琐。 截面法：适用于求指定杆件的内力，但用它来求全部杆件的内力时，工作量要比 结点法大得多。 应用时，要根据题目的要求适当选择计算方法。
FP
FP I
C
1 0 2a
Fx3 Fy3 / 2 0.75FP。
0A
00
3a
l
5
FN 3 Fy 3 l y 1.5FP 2
2.5FP
a
D 4I a
1.68FP (压)。
MC 0，
FN 4
1 2a
《截面法求内力》课件
适用范围广：适用 于各种类型的结构 ，如梁、板、壳等
便于分析：可以方 便地分析结构的局 部应力和应变，为 优化设计提供依据
缺点
适用范围有限：仅适用于线弹 性材料，不适用于塑性材料
计算复杂：需要求解多个方 程，计算量大
精度有限：对于复杂结构，截 面法求解的内力可能与实际值
有较大偏差
难以处理非均匀材料：对于非 均匀材料，截面法求解的内力
梁的内力分析
梁的受力分析：确定梁的受力情况，包括轴力、剪力和弯矩 截面法求内力：利用截面法求解梁的内力，包括轴力、剪力和弯矩 实例分析：选取一个具体的梁结构，进行内力分析，包括轴力、剪力和弯矩的计算 结论：总结梁的内力分析方法，以及如何利用截面法求解梁的内力
圆轴的内力分析
圆轴的受力情况： 轴向力、扭矩、弯 矩等
截面法的应用范围
材料力学：用于求解材料的 应力和应变
结构力学：用于求解杆件的 内力、应力和变形
土木工程：用于计算桥梁、 隧道、建筑物等结构的内力
机械工程：用于计算机械零 件的内力、应力和变形
截面法求内力的 步骤
确定截面位置
确定截面位置：选择合适的截面位置，以便于计算内力 截面形状：选择合适的截面形状，如矩形、圆形等 截面尺寸：确定截面的尺寸，如长度、宽度、厚度等 截面材料：确定截面的材料，如钢、铝、混凝土等 截面受力：确定截面所受的力，如拉力、压力、剪力等 截面内力：根据截面所受的力，计算截面内力，如轴力、剪
截面法求内力的步 骤：确定截面、建 立平衡方程、求解 内力
实例分析：某圆轴 在轴向力、扭矩、 弯矩作用下的内力 分析
结论：截面法求内 力是一种有效的方 法，可以准确计算 出圆轴的内力。
截面法求内力的 注意事项
简述截面法计算内力的步骤
简述截面法计算内力的步骤
截面法是一种结构力学分析的方法，用于计算结构中截面处的内力。
以下是使用截面法计算内力的步骤：
1. 确定截面：根据结构的几何形状和所需计算的截面位置，确定需要计算的截面。
2. 建立截面坐标系：在确定的截面处，建立适当的坐标系，通常使用弯矩轴线和剪力轴线作为坐标轴。
3. 计算剪力：在截面上计算受力情况，包括剪力和轴向力。
剪力可以通过受力平衡或应力分布方法进行计算。
4. 计算弯矩：在截面上计算受力情况，包括弯矩和轴向力。
弯矩可以通过弯曲公式和应力分布方法进行计算。
5. 绘制剪力图和弯矩图：根据计算得到的剪力和弯矩在截面上的分布情况，绘制剪力图和弯矩图。
6. 分析内力：根据截面上的剪力和弯矩分布，分析各个部分的内力情况，包括剪力内力和弯矩内力。
7. 分析截面的承载力：根据截面的几何特性和材料的强度，分析截面的承载力情况，包括抗弯承载力和抗剪承载力。
通过以上步骤，可以得到截面处的剪力和弯矩分布情况，以及
各个部分的内力情况。
这些结果可以用于结构设计和分析中的其他计算和决策。
截面法求桁架杆件内力
截面法1截面法可以快速求出某一内力，通常取结构 的一部分为隔离体，其上力系为平面一般力系。
每个隔离体上有3个独立平衡方程。
一般表示 为： ∑ FX = 0 投影法 ∑ FY = 0 力矩法 ∑M = 0 计算要点： 尽量使一个方程解一个未知数，避免求解 联立方程。
一. 力矩法例：求图示桁架1、2、3杆的轴力。
2VAVB解：由整体平衡条件求得支座反力 VA=VB HA=0作Ⅰ--Ⅰ截面,截开1、2、3杆的轴力 取截面以左为隔离体。
Ⅰ3Ⅰ（1）求1杆轴力N1K14选取未知力N2和N3 延长线的交点K1作 为取矩点。
N1 对K1点取矩，由 ∑MK1 = 0 从而求出所求未知 力N1。
VA（2）求2杆轴力N2N2 K2 VAY252X2由∑MK2 = 0 ,比例关系从而求出所求未知力Y2。
2杆轴力N2（3）求3杆轴力N3Y3 N3 X3K3 VA6由 ∑MK3 = 0比例关系从而求出所求未知力X3。
3杆轴力N3力矩法要点：7欲求某指定杆内力，则作一截面，截开待求 杆； 隔离体上除所求未知力外，其余未知力的延 长线均交于某一点K。
对K点取矩，从而求出所求未知力 。
（1）选择其余未知力延长线的交点K作为取矩 点，从而用∑MK=0，求出指定杆内力。
（2）将斜杆的内力放在某一个合适的点上分 解，使其一个分力通过取矩点K。
例1. 求图示桁架杆件a、b、c的轴力890kN30kN作Ⅰ—Ⅰ截面Ⅰ9Ⅰ求NaNa 求Na时，对另 外两个未知力的 交点C取矩，10C由 ΣMc＝0，得 Na×4＋30×8＝030kN解得： Na =－ 60kN求NbD Xb E Yb Nb30kN11求Nb时，对点D取矩。
将Nb 其在E点处分解 为水平和竖向分量。
由ΣMD＝0，得 Yb×12＋40×4 － 30×12＝0 解得 Yb＝16.67 kN由比例关系得到：N b = 2Yb = 2 × 16.67 = 23.57kN求NcYc XcD Nc12求Nc时，对点E取矩。
第四讲 内力与截面法
§1.3.2 截面法
求内力的方法：截面法
m
m
m m
m m
ΣF = 0 ΣM = 0
§1.3.2 截面法
求内力的方法：截面法
把分析对象作为处于准静态的刚体看待
平衡条件 （力及其力矩）
外力与外力平衡 外力与内力平衡 内力与内力平衡
}
§1.3.2 截面法
求内力的方法：截面法 例：求钻床截面m-m上的内力。
x
FN
m
m m
m
mБайду номын сангаасm
2、代替：任取一部分，该部分上弃去部分对其的作用，用作用在截 面上相应的内力（力或力偶）代替。
§1.3.2 截面法
求内力的方法：截面法
m
m m
m
m m
3、平衡：对留下部分建立平衡方程，根据其上已知外力来计算杆在截 开面上的未知内力（此时截开面上内力对所留部分而言是外力）。
有缘学习更多＋谓ｙｇｄ３０７６或关注桃报：奉献教育（店铺）
§1.3.2 截面法
求内力的方法：截面法 例：求钻床截面m-m上的内力。 解：用截面m-m将钻床截为两部分，
取上半部分为研究对象， 受力如图，列平衡方程：
Y = 0 FN = P
Mo(F) = 0
m
Pa− M = 0
M = Pa
M
有缘学习更多＋谓ｙｇｄ３０７６或关注桃报：奉献教 育（店铺）
y
P
a
m
§1.3.1 内力
内力（internal forces）：外力作用引起构件内部的附加相互作用力。
内力的本质是原子 间的电磁作用
§1.3.2 截面法
求内力的方法：截面法
F1
1、截开：在所求内力的截面处，假想 地用截面m-m将杆件一分为二。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A
J
lJK
K
B 支梁，作出简支梁在外荷载作用下的弯矩 图，叠加到基线上（弯矩竖标叠加），最
后所得图线就是实际的弯矩图。
M JK J
F QJKMຫໍສະໝຸດ JK JF Jy1lJK
J M JK
截面法
q
M JK
lJK
K
M KJ 受力等效
J
F QKJ
F Jy
荷载叠加
M JK
M KJ K
J
JJ
K
M JK
FKy1 FJy2
M
L C
80 kN
m
（3）计算点C右截面的内力
C
M
R C
40kN FNRC 0 FQRC 40kN
M
R C
80 kN
m
内力图：表示结构上各截面的内力随横截面位置变化规律的图形。
列方程作内力图
FP x
A
Ca B
l
FP
+
FQ图 FP(l-a)
截面法
剪力方程 弯矩方程
FQ FQ x M Mx
FQ B
时，先分别作出各荷载单独作用 下的内力图，再将各个内力图的 竖标相叠加（代数和），便得到 各荷载共同作用下的内力图。
2FP FPa
AC
DB
a
a
a
2FP AC
DB
a
a
a
FPa
AC
DB
a
a
a
用分段叠加法绘弯矩图
对于直杆区段，用截面法求出该段两
端的截面弯矩后，将两个竖标的顶点以虚
FP
q
M 线相连，并以此为基线，再将该段作为简
x
q=20kN/m
F Ax
A
C
FP=40kN DB
FAx 0 FAy 70kN() FBy 50kN()
F Ay 70 +
A
A
4m
2m 2m
F By
A
EC D 10 10 -
B 70
50 50
FQ
FQ图（单位kN）
M
F EC D B
q FQ FQ 70 20x
M 70x 10x2
M
40 B
FQ 10
50 M 160 10x
(0 x 4) (0 x 4)
(4 x 6) (4 x 6)
100 120 100 122.5
M 图（单位kN.m）
FQ M
B
FQ 50 (6 x 8)
50 M 400 50x (6 x 8)
叠加法
条件：结构线弹性、小变形
荷载叠加法： 当结构上同时作用有许多荷载
3a 2
0
ME
3FP a 2
FQE FPa
D
B
ME E
FP
Fy 0
3
FQE FBy 0
FQE
FP 3
ME 0
ME
FP a
FP 3
3a 2
0
ME
3FP a 2
例2 图示为在截面C处承受一斜向集中力的简支梁。试求截面 C处左、 右两截面的内力。
（1）计算梁的支座反力
(a) (a)
F F
Ax Ax
平: 对留下部分写平衡方程求出内力的值
FQ(+)
FQ(+)
M(+)
M(+)
（1）平衡方程的正负和内力的正负是完全不同性质的两套符号系统。 （2）取简单部分作为隔离体，列平衡方程时，尽量使一个方程含有一个未知量
例1 求E截面内力
A FAx
FAy
2FP FPa
C
D
1.5a E
a
a
a
2. 用截面法研究内力
6600FkkNNAy
2m
A
6044k00NkkNN A
CCMMMFFCLCCLLQQ2LLCCmFFF
L NLC NC
L NC
F By
40kN FFACCRR
F
CRMM
R CR C
C CCFFFFQQQRQRRCCCLC
BB B4400kkNN
（2）计算点C左截面的内力
FNLC 60kN
FQLC 40kN
A
B
l
ql
+
FQ图
1 ql 2 2
1 ql 2 8
M图
FQ q M
FQ＝qx 0 x l
B
M＝ 1 qx2 2
0 x l
x FP
A
C
a
FAy
b l
FPb l
+
FP a
-
l FQ图
FPab M图
l
B FBy
A FPb
l
FQ
M
MA 0
Fy 0
FBy
FP a l
FAy
FPb l
FQ
FQ
FPb l
(0 x a)
M
M FPb x (0 x a)
l
B
FQ
FP a l
(a x l)
FPa M FPa (l x)
l
l
(a x l)
x A FAy
M0
C
B
a l
b FBy
MA 0
Fy 0
FBy
M0 l
FAy
M0 l
M0 l
+
FQ图
M 0b l
M 0a l
M图
A M0 l
FQ
M
FQ
lJK
FKy2 F Jy
M KJ
K+
ql2 8
=J M JK
q M KJ
K
lJK q
ql2 lJK8
FQ
M0 l
M M M0 x
l
(0 x a) (0 x a)
B
FQ
M0 l
(a x l)
M 0 M M 0 (l x) (a x l)
l
l
x
A FAy
ql 2
+
q l
FQ图
ql 2 8
M图
B
MA 0
FBy
ql 2
FBy
Fy 0
FAy
ql 2
-
q FQ
ql FQ 2 qx
解： 1. 确定支座反力
B Fx 0 MA 0
FBy
Fy 0
FAx 0 2FPa FPa FBy 3a 0 FAy FBy 2FP 0
FBy
FP 3
FAy
5FP 3
2FP FQE
A 5FP
C E ME
3
Fy 0
2FP
FQE
5FP 3
0
FQE
FP 3
ME 0
ME
2FP
a 2
5F 3
受弯构件
M
M
梁：以弯曲变形为主的构件
纯弯曲
P/2
P/2
P
剪切和弯曲
静定梁的基本形式
(a)
简支梁
(b)
伸臂梁
(c)
悬臂梁
计算杆件内力的基本方法：截面法
m
A
m
l
M FN
FQ
FN(+)
FN(+)
切: 假想沿指定横截面将杆切开
B 留: 留下左半段或右半段，标注荷载和反力
代: 将抛掉部分对留下部分的作用用内力代替
M
FQ＝0
M＝0
0 x a
0 x a
FQ FP B
C M
FQ＝FP a x l
M＝ FP (x a) a x l
M图
M0 x
A
C
B a
l
FQ图 M0 M图
FQ B
M
FQ＝0
M＝0
0 x a
0 x a
FQ M0 B
C M
FQ＝0 a x l
M＝M0 a x l
x q
AA
FFF44PPP33===1CC11000000kkkNNN
BB
(a)
F Ax A
FF
Ay Ay
22mm43 C
22mm
B
FF
By By
Fx 0 : FAx 60kN( ) MB 0: FAy 40kN()
Fy 0 : FBy 40kN()
((bb)) (b) ((cc)) (c)
(0 x l)
ql
A
2
ql
2
M
M ql x q x2
(0 x l)
22
FP
M0
FP
FQ图
+
FP(l-a)
M图
M0
FP 内力图形状特征 M0
FPb l
+
FQ图 FPa
-
l
M0 l
+
M 0b l
M图
FP ab l
M 0a l
q
ql
+
1 ql 2 2
1 ql 2 8
q
ql 2
+ ql -
2
ql 2 8