截面法求内力完整版本
第二章 杆件的内力.截面法(第1、2、3节)
外 无外力段
力
q=0
均布载荷段
q>0
q<0
集中力
P C
集中力偶
m
C
水平直线
斜直线
自左向右突变 无变化
FS 图
FS
特
征
x
FS >0
FS
FS
x
x
FS <0 增函数
FS
FS FS1
C
x
FS2
x
降函数 FS1–FS2=P
FS
C x
M
斜直线
曲线
自左向右折角 自左向右突变
图M
M
M
M
M
与 M M1
特
x
x
x
x
xm
x
求:外力偶矩Me ( N·m)
解:PMe
n 30
P1000Me3n0
由此求得外力偶矩:
Me
Me
P103 00 P
M e
n
954 (N .9 m) n
若传递功率单位为马力(PS)时, 由于PS=735.5N·m/s
Me
702P4(N.m) n
杆件的内力.截面法
对称弯曲:工程中最常见的梁,其横截面一般至少有一根对称 轴,因而整个杆件有一个包含轴线的纵向对称面。 若所有外力都作用在该纵向对称面内时,梁弯曲变 形后的轴线将是位于该平面内的一条曲线,这种弯 曲形式称为对称弯曲。
注意 1、用截面法求轴力时,在切开的截面上建议假设正 的轴力,由平衡方程得出的FN值为正,说明轴力为正 (拉力); FN值为负,说明轴力为负(压力)。
2、在画轴力图时,填充为下画线或无填充,不要画剖 面线形式;并注上 符号 或 。
第二章 杆件的内力.截面法(第1、2、3节)

1.截面法(Method of sections) (1)截 F 在求内力的截面m-m 处, 假想地将杆截为两部分. m m F
(2)取 取左部分部分作为研 究对象. (3)代 弃去部分对研究对象 的作用以截开面上的内力 F m F
M M M M 图 M x x x x x 特 征 增函数 降函数 盆状 伞状 折向与P反向
水平直线
斜直线
自左向右突变 FS F 1
无变化
与 m 同
MM 1
x
M2 M1 M 2 m
或
弯矩图 的特征
一般斜直线 下凸的二 次抛物线 或
在C处有突变
与 m 同
最大弯矩 所在截面 可能位置
在FS=0的截面
在剪力突变 的截面
在紧靠C的某 一侧截面
m
剪力、弯矩与外力间的关系 外 力 无外力段
q=0
均布载荷段
q>0 q<0
集中力
P C
集中力偶
m C
FS FS FS FS FS FS S 图 C C 特 x x x x x x FS2 征 FS >0 FS <0 增函数 降函数 FS1–FS2=P 自左向右折角 自左向右突变 斜直线 曲线 M
m F m m FN
代替,合力为FN .
(4)平 对研究对象列平衡方程
式中:FN 为杆件任一横截面 mm上的内力.与杆的轴线重合,
即垂直于横截面并通过其形心,
称为轴力(axial force)。
FN = F
注意 1、用截面法求轴力时,在切开的截面上建议假设正 的轴力,由平衡方程得出的FN值为正,说明轴力为
截面法求杆件的内力

截面法求杆件的内力教学目标:1、理解和掌握求杆件内力的方法——截面法;2、熟练运用截面法求不同杆件受到拉伸时的内力。
教学重点:截面法求杆件内力的步骤。
教学难点:如何运用截面法求内力的方法解决工程力学中求内力的实际问题。
教学方法:提出问题——实例演示——练习点拨——归纳总结教学过程:一、复习旧知1、杆件有哪几种基本变形?2、拉伸和压缩的受力特点是什么?3、拉伸和压缩的变形特点是什么?二、新课讲解思考:当杆件受到拉伸、压缩时,就会在杆件内部产生力的作用,怎样才能确定杆件的内部会产生多大的力?(引出课题)出示本节课的学习目标。
(一)、教学什么是杆件的内力?内力:杆件在外力作用下产生变形,其内部相互间的作用力称为内力。
一般情况下,内力将随外力增加而增大。
当内力增大到一定限度时,杆件就会发生破坏。
内力是与构件的强度密切相关的,拉压杆上的内力又称为轴力。
(二)、教学截面法求杆件的内力。
1、什么是截面法?截面法:将受外力作用的杆件假想地切开,用以显示内力的大小,并以平衡条件确定其合力的方法,称为截面法。
它是分析杆件内力的唯一方法。
2、实例演示:如图AB 杆受两个力,一个向左,一个向右,大小均为F 。
作用点分别为A 和B 。
①、确定要截开的次数和位置(要根据杆件的受力情况而定) ②、选取一半截面为研究对象(一般选取受力较少的一段作为研究对象)③、假设出截面上的内力(取左段内力向右设,取右段内力向左设,方向跟坐标轴方向一致,左负右正、下负上正)④、用平衡方程求出截面上的内力(求出的内力为正值为拉力,负值为压力)取左段 ∑Fx=O -F +FN =0 取右段 ∑Fx=O F -FN =0FN =F FN =F 3、总结截面法求杆件内力的步骤:(1)截:在需求内力的截面处,沿该截面假想地把构件切开。
(2)取:选取其中一部分为研究对象。
(3)代:将截去部分对研究对象的作用,以截面上的未知内力F F N来代替。
(4)平:根据研究对象的平衡条件,建立平衡方程,以确定未知内力的大小和方向。
02截面法求内力基本方法
0 -33 34.8
19
19
Y 0 YNAD 11 kN YNAD CD 0.5 X NAD AC 1.5 X NAD 3YNAD 33 kN
X 0 FNAC 33 kN
0 -33
-33
34.8 -8
19
19
0 -33
-33
34.8
dM dx
FQ ,
dFQ q( x), dx
dFN p( x) dx
Mq
M+dM
dx
FN
dx
FN+d FN
FQ
FQ+dFQ
dM dx
FQ ,
dFQ q( x), dx
dFN p( x) dx
集中力
梁上 无外力 均布力作用 集中力作用 偶M作 铰处
情况
(q向下)
处(FP向下) 用处
斜直 剪力图 水平线 线(
)
为 零 处
有突 变(突 变值=
FP)
如 变 号
无 无变化 影
响
一般 抛物 有 有尖 有 有突变
弯矩图 为斜 线(
极 角(向 极 (突变 为零
直线 下凸) 值 下) 值 值=M)
曲杆微分关系
曲杆微段
dFN ds
=-qt+
FQ R
dFQ ds
=qn-
FN R
dM ds
=FQ-m
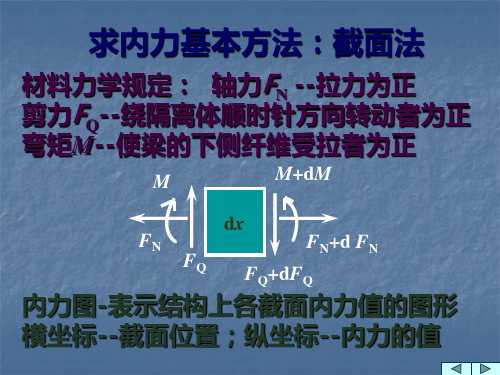
求内力基本方法:截面法
材料力学规定: 轴力FN --拉力为正 剪力FQ--绕隔离体顺时针方向转动者为正
弯矩M--使梁的下侧纤维受拉者为正
M
M+dM
试述求杆件横截面上内力的截面法步骤和方法

试述求杆件横截面上内力的截面法步骤和方法1. 了解截面法哎,说到工程力学里的截面法,别让这些名字吓坏了,其实就是一种找出杆件内部力量的简单方法。
咱们平常接触的建筑物、桥梁,或者一些机械构件,都是通过这种方法来确保它们的稳固和安全的。
这个方法简单来说就是用“剪刀”切一刀,把杆件“分尸”,然后分析切面上受力的情况。
好比是咱们剥苹果皮,剥开之后看里面的果肉,这样能更清楚地了解苹果的质量。
2. 截面法的步骤2.1 选取截面首先,挑选一个合适的截面,瞅准了方向之后,就下手了。
这个步骤就像在你脑子里画出一条切割线。
你得选择一个合适的位置,把杆件从中间“切开”。
这里要注意,选取的位置一定要使得切面上的力易于计算。
如果这个位置选错了,结果就像你在黑暗中找钥匙一样,费劲不讨好。
2.2 画出受力图接下来,别忘了给这片“切面”画上图。
要把杆件切开后,分离出的部分的受力情况画出来。
图上得标明各种内力,比如剪力、轴力和弯矩等等。
这些力就像是在打游戏时,你需要记录你的角色的状态和装备一样,你要准确记录这些力的情况,这样才能确保你计算的准确。
2.3 列出平衡方程然后,你就要写平衡方程了。
平衡方程是用来保证杆件在切开时的受力状态是平衡的,不会乱七八糟。
这些方程包括了力的平衡、力矩的平衡等。
就像你玩积木,如果要保持积木塔不倒,就得仔细计算每一块积木的放置位置。
2.4 解方程找内力最后,你要解这些方程,找出杆件内部的力量。
就像做数学题一样,把方程算出来,你就能得到具体的内力数值。
这个步骤可不能马虎,不然得到的结果就像是空话,没有实际意义。
3. 截面法的应用3.1 结构分析截面法在结构分析中的应用非常广泛。
无论是大桥、小楼,还是家里的门框,都是用这个方法来确保结构的安全性。
就像是大厨做菜,得先知道每种材料的用量和比例,才能做出美味的菜肴。
工程师用截面法就像是这个大厨,通过计算内力,确保建筑的稳定性和安全性。
3.2 机械设计在机械设计中,截面法也是必不可少的。
截面法求桁架杆件内力

截面法1截面法可以快速求出某一内力,通常取结构 的一部分为隔离体,其上力系为平面一般力系。
每个隔离体上有3个独立平衡方程。
一般表示 为: ∑ FX = 0 投影法 ∑ FY = 0 力矩法 ∑M = 0 计算要点: 尽量使一个方程解一个未知数,避免求解 联立方程。
一. 力矩法例:求图示桁架1、2、3杆的轴力。
2VAVB解:由整体平衡条件求得支座反力 VA=VB HA=0作Ⅰ--Ⅰ截面,截开1、2、3杆的轴力 取截面以左为隔离体。
Ⅰ3Ⅰ(1)求1杆轴力N1K14选取未知力N2和N3 延长线的交点K1作 为取矩点。
N1 对K1点取矩,由 ∑MK1 = 0 从而求出所求未知 力N1。
VA(2)求2杆轴力N2N2 K2 VAY252X2由∑MK2 = 0 ,比例关系从而求出所求未知力Y2。
2杆轴力N2(3)求3杆轴力N3Y3 N3 X3K3 VA6由 ∑MK3 = 0比例关系从而求出所求未知力X3。
3杆轴力N3力矩法要点:7欲求某指定杆内力,则作一截面,截开待求 杆; 隔离体上除所求未知力外,其余未知力的延 长线均交于某一点K。
对K点取矩,从而求出所求未知力 。
(1)选择其余未知力延长线的交点K作为取矩 点,从而用∑MK=0,求出指定杆内力。
(2)将斜杆的内力放在某一个合适的点上分 解,使其一个分力通过取矩点K。
例1. 求图示桁架杆件a、b、c的轴力890kN30kN作Ⅰ—Ⅰ截面Ⅰ9Ⅰ求NaNa 求Na时,对另 外两个未知力的 交点C取矩,10C由 ΣMc=0,得 Na×4+30×8=030kN解得: Na =- 60kN求NbD Xb E Yb Nb30kN11求Nb时,对点D取矩。
将Nb 其在E点处分解 为水平和竖向分量。
由ΣMD=0,得 Yb×12+40×4 - 30×12=0 解得 Yb=16.67 kN由比例关系得到:N b = 2Yb = 2 × 16.67 = 23.57kN求NcYc XcD Nc12求Nc时,对点E取矩。
截面法计算内力的步骤

截面法计算内力的步骤截面法计算内力的步骤如下:1.确定截面:根据结构的几何形状和所需计算的截面位置,确定需要计算的截面。
2.建立截面坐标系:在确定的截面处,建立适当的坐标系,通常使用弯矩轴线和剪力轴线作为坐标轴。
3.计算剪力:在截面上计算受力情况,包括剪力和轴向力。
剪力可以通过受力平衡或应力分布方法进行计算。
4.计算弯矩:在截面上计算受力情况,包括弯矩和轴向力。
弯矩可以通过剪力和轴向力的计算结果进行进一步计算。
5.建立平衡方程:根据截面上的剪力和弯矩的计算结果,建立平衡方程。
平衡方程可以根据结构的具体情况建立,通常需要考虑截面上的所有力和力矩的平衡条件。
6.解平衡方程:解平衡方程以确定未知内力。
解方程时可能需要考虑结构的刚度和惯性等物理特性。
7.确定内力值:根据解出的未知内力和已知的剪力和弯矩的计算结果,确定内力值。
内力可以是拉力或压力,也可以是弯矩。
以上步骤可以帮助您使用截面法计算内力。
需要注意的是,具体的计算步骤可能会因结构的不同而有所差异,因此在进行内力分析时需要结合具体情况灵活运用各种方法。
截面法计算内力的优点和缺点如下:优点:1.简单易行:截面法是一种简单直观的方法,易于理解和计算。
2.可适用于多种结构形式:截面法可以适用于多种结构形式,如梁、板、柱等,因此在工程实践中得到广泛应用。
3.可以考虑多种内力:截面法不仅可以计算剪力和弯矩,还可以考虑拉力、压力等其他内力。
4.可用于静力分析和动力分析:截面法不仅可用于静力分析,即求结构在恒定载荷下的内力,还可用于动力分析,即求结构在动载荷下的内力。
缺点:1.精度有限:截面法是一种近似方法,其精度取决于所取的截面和所用的简化假定。
对于复杂结构,可能需要采用更精确的方法进行内力分析。
2.对经验要求高:使用截面法进行内力分析需要具备一定的工程经验和对结构的理解,否则可能会出现误差或遗漏。
3.对初始条件敏感:截面法的计算结果对初始条件(如初始剪力和弯矩)较为敏感,因此在进行内力分析时需要注意初始条件的设定。
截面法求内力讲解
解: 1. 确定支座反力
B Fx 0 MA 0
FBy
Fy 0
FAx 0 2FPa FPa FBy 3a 0 FAy FBy 2FP 0
FBy
FP 3
FAy
5FP 3
2FP FQE
A 5FP
C E ME
3
Fy 0
2FP
FQE
5FP 3
0
C
a
FAy
b l
FPb l
+
FP a
-
l FQ图
FPab M图
l
B FBy
A FPb
l
FQ
M
MA 0
Fy 0
FBy
FP a l
FAy
FPb l
FQ
FQ
FPb l
(0 x a)
M
M FPb x (0 x a)
l
B
FQ
FP a l
(a x l)
FPa M FPa (l x)
平: 对留下部分写平衡方程求出内力的值
FQ(+)
FQ(+)
M(+)
M(+)
(1)平衡方程的正负和内力的正负是完全不同性质的两套符号系统。 (2)取简单部分作为隔离体,列平衡方程时,尽量使一个方程含有一个未知量
例1 求E截面内力
A FAx
FAy
2FP FPa
C
D
1.5a E
a
a
a
2. 用截面法研究内力
M JK J
F QJK
M JK J
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§7-2 拉 伸 和 压 缩 时 截 面 上 的 内 力
二、截面法求内力
前面学过的方法已经不能求内力了, 为了确定在外力作用下构件所产的内 力的大小和方向,我们采用了一种新 的方法——截面法
截
1、确定外力个数及作用点
面
法
求
内
力 如图AB杆受两个力,一个向左,一个向右,大小均为 的 F。作用点分别为A和B。
当杆件受外力作用时,各颗粒间的相对位置将 会发生改变,引发颗粒间内力也要变化。我们把这 种杆件内部由于外力作用而产生的相互作用力的改 变量称为内力。而且内力与外力的关系是:内力是 因外力而产生的(当外力解除时,内力也随之消失) 外力越大,内力越大,当内力超过一定限度,工件 就会产生破坏。
其大小和分部情况与杆件变形、破坏有密切联 系,所以我们必须把内力求出。
注:外力有两种
步 一、载荷:在图上用“→”标出,并注明大小的那个。 骤 二、约束反力:图上未标出,要自己分析。有约束反
力的地方必画有除研究对象以外的物体。
截
2、确定要截开的次数和位置
面
法
求
1
内
力
1
的 以外力的作用点为分界点,将杆件分段。每段必须也
步 骤
只需截开一次。在截开前我们在原图上标出截面, 并按1-1、2-2、3-3……命名。
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!
力 解:-F+FN1=0 的 FN1=F(拉) 步 注: 骤 1 、力正负的规定:
列方程时,左负右正,下负上正。和坐标轴的 规定一致。
2 、求出的结果为正值表示受拉伸,负值表示压缩。
练习题
练 习 题
作业
布 第七章:
置 ➢ 一、1-5
作 业
➢ 二、1-5 ➢ 三、1-5 ➢ 四、1-4
➢ 五、1、5、6
截
4、假设出截面上的正应力
面
法
求
内
力 为了保证所截部分仍然保持静止,必须假设出截面上 的 的内力。并以其所在截面的名称对其命名。
步 注:内力的假设原则
骤 1、拉、压时内力垂直于截面。 2、选左边为研究对象,内力向右设;选右边为研究
对象,内力向左设。
截
5、用平衡方程求出截面上的内力
面
法
求
内 列出平衡方程,求出横截面上的内力。
拉伸和压缩的概念和截面法求内力
课件
新乡市高级技工学校(三技校) 赵志强
复习提问
1、材料力学的内容、研究对象和任务 分别是什么?
2、什么是承载能力?它有哪三个衡量 面?分别表示什么意义?
3、杆件有哪几种基本变形?
§7-1 拉
拉伸和压缩的受力特的特点:作用在杆端的两外力(或外力的合力) 念 大小相等,方向相反,力的作用线与杆件的轴线重
截
3、假设截面截开选一半为研究对象
面
法
求
内 按顺序从1-1截面开始,假设截面截开,选一半为研 力 究对象,并另行画出所选部分的视图。
的 注:选哪一半为研究对象的原则 步 1、哪一半无约束反力(在原图上不和其它物体接
触),选哪一半为研究对象。
骤 2、哪一半受力简单(受力少),选哪一半为研究对 象。
3、如果以上两条两边都一样,那么随便选哪一边都 可以。
合。
§7-1 拉
拉伸和压缩的变形特点
伸
和
压
缩
的
概 变形的特点:杆件沿轴线方向伸长(拉伸时)或缩短 念 (压缩时)。
§7-2 拉 伸 和 压 缩 时 截 面 上 的 内 力
一、内力的定义
物体是由无数颗粒(原子)组成的,在其未受 外力作用时就存在相互作用力(引力和斥力),以 维持它们之间的联系及物体的原有形状。
