反向传播和梯度下降法
2、lstm反向传播计算梯度的公式

LSTM(Long Short Term Memory)是一种循环神经网络,它在处理长序列数据时比传统的循环神经网络具有更好的效果。
LSTM的核心是其能够长期记忆和选择性遗忘的机制,这使得它能够更好地处理长序列数据的依赖关系。
LSTM的反向传播算法是指在训练网络时,通过梯度下降来更新网络参数。
在LSTM中,反向传播算法的关键是计算损失函数对网络参数的梯度。
下面我们将介绍LSTM反向传播算法中计算梯度的公式。
1. 遗忘门(Forget Gate)在LSTM中,遗忘门用来控制从细胞状态中丢弃哪些信息。
遗忘门的输出由sigmoid函数计算得到,其公式如下:\[f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)\]其中,\(f_t\)为遗忘门的输出,\(W_f\)为遗忘门的权重矩阵,\(h_{t-1}\)为上一个时刻的隐藏状态,\(x_t\)为当前时刻的输入,\(b_f\)为偏置项。
通过遗忘门,LSTM网络可以选择性地丢弃以往信息,从而实现长期记忆的机制。
2. 输入门(Input Gate)输入门用来控制哪些信息可以被加入到细胞状态中。
输入门的输出由sigmoid函数计算得到,其公式如下:\[i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)\]其中,\(i_t\)为输入门的输出,\(W_i\)为输入门的权重矩阵,\(h_{t-1}\)为上一个时刻的隐藏状态,\(x_t\)为当前时刻的输入,\(b_i\)为偏置项。
3. 候选值(Candidate)候选值用来更新细胞状态的候选值,其计算公式如下:\[\tilde{C}_t = tanh(W_C \cdot [h_{t-1}, x_t] + b_C)\]其中,\(\tilde{C}_t\)为候选值,\(W_C\)为候选值的权重矩阵,\(h_{t-1}\)为上一个时刻的隐藏状态,\(x_t\)为当前时刻的输入,\(b_C\)为偏置项。
前向传播和反向传播

前向传播和反向传播1、前向传播算法所谓的前向传播算法就是:将上一层的输出作为下一层的输入,并计算下一层的输出,一直到运算到输出层为止。
对于Layer 2的输出 a_{1}^{(2)} ,a_{2}^{(2)},a_{3}^{(2)},a_{1}^{(2)}=\igma(z_{1}^{(2)})=\igma(w_{11}^{(2)}_{1}+w_{12} ^{(2)}_{2}+w_{13}^{(2)}_{3}+b_{1}^{(2)})a_{2}^{(2)}=\igma(z_{2}^{(2)})=\igma(w_{21}^{(2)}_{1}+w_{22} ^{(2)}_{2}+w_{23}^{(2)}_{3}+b_{2}^{(2)})a_{3}^{(2)}=\igma(z_{3}^{(2)})=\igma(w_{31}^{(2)}_{1}+w_{32} ^{(2)}_{2}+w_{33}^{(2)}_{3}+b_{3}^{(2)})对于Layer 3的输出a_{1}^{(3)},a_{1}^{(3)}=\igma(z_{1}^{(3)})=\igma(w_{11}^{(3)}a_{1}^{(2)} +w_{12}^{(3)}a_{2}^{(2)}+w_{13}^{(3)}a_{3}^{(2)}+b_{1}^{(3)}) a_{2}^{(3)}=\igma(z_{2}^{(3)})=\igma(w_{21}^{(3)}a_{1}^{(2)} +w_{22}^{(3)}a_{2}^{(2)}+w_{23}^{(3)}a_{3}^{(2)}+b_{2}^{(3)})从上面可以看出,使用代数法一个个的表示输出比较复杂,而如果使用矩阵法则比较的简洁。
将上面的例子一般化,并写成矩阵乘法的形式,z^{(l)}=W^{(l)}a^{(l-1)}+b^{(l)}a^{(l)}=\igma(z^{(l)})其中 \igma 为 igmoid 函数。
梯度下降优化算法

梯度下降优化算法综述,梯度下降法梯度下降法是什么?梯度下降法(英语:Gradientdescent)是一个一阶最优化算法,通常也称为最陡下降法。
要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。
如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
梯度下降一般归功于柯西,他在1847年首次提出它。
Hadamard在1907年独立提出了类似的方法。
HaskellCurry在1944年首先研究了它对非线性优化问题的收敛性,随着该方法在接下来的几十年中得到越来越多的研究和使用,通常也称为最速下降。
梯度下降适用于任意维数的空间,甚至是无限维的空间。
在后一种情况下,搜索空间通常是一个函数空间,并且计算要最小化的函数的Fréchet导数以确定下降方向。
梯度下降适用于任意数量的维度(至少是有限数量)可以看作是柯西-施瓦茨不等式的结果。
那篇文章证明了任意维度的两个向量的内(点)积的大小在它们共线时最大化。
在梯度下降的情况下,当自变量调整的向量与偏导数的梯度向量成正比时。
修改为了打破梯度下降的锯齿形模式,动量或重球方法使用动量项,类似于重球在被最小化的函数值的表面上滑动,或牛顿动力学中的质量运动在保守力场中通过粘性介质。
具有动量的梯度下降记住每次迭代时的解更新,并将下一次更新确定为梯度和前一次更新的线性组合。
对于无约束二次极小化,重球法的理论收敛速度界与最优共轭梯度法的理论收敛速度界渐近相同。
该技术用于随机梯度下降,并作为用于训练人工神经网络的反向传播算法的扩展。
梯度下降算法是指什么神经网络梯度下降法是什么?梯度下降法是一个最优化算法,通常也称为最速下降法。
最速下降法是求解无约束优化问题最简单和最古老的方法之一,虽然现已不具有实用性,但是许多有效算法都是以它为基础进行改进和修正而得到的。
最速下降法是用负梯度方向为搜索方向的,最速下降法越接近目标值,步长越小,前进越慢。
多个loss损失反向传播的原理

多个loss损失反向传播的原理反向传播算法是深度学习中广泛使用的一种优化算法,用于通过梯度下降更新模型参数来减小网络的损失。
在多个loss损失函数存在的情况下,反向传播算法可以同时计算每个loss对应的梯度,并将这些梯度累加起来,最后更新模型参数。
1. 多个loss损失函数的定义在深度学习中,为了训练一个模型,通常会定义一个主要的损失函数,比如交叉熵损失函数。
然而,在一些情况下,我们还可能定义一些辅助的损失函数,用于提供额外的信息或帮助网络学习更好的特征。
这些辅助损失函数通常会在网络结构的不同层中引入,并与主要损失函数一起构成多个loss。
2.梯度的计算在多个loss损失函数存在的情况下,反向传播算法的第一步是计算每个loss的梯度。
以主要损失函数和一个辅助损失函数为例,对于第i个loss函数,其梯度可以通过链式法则计算得到:∂Loss/∂w = ∑ ∂Loss / ∂(loss_i) * ∂loss_i/∂w其中w表示模型参数,Loss表示总的损失函数,loss_i表示第i个损失函数。
上式中的第一项∂Loss / ∂(loss_i)可以通过对Loss函数对loss_i的求导得到,第二项∂loss_i/∂w是辅助损失函数对参数w的梯度。
3.梯度的累加与更新计算得到每个loss函数的梯度后,反向传播算法会将这些梯度累加起来,并根据累加的梯度来更新模型参数。
具体而言,假设有n个loss 函数,对于模型参数w的更新可以表示为:w_new = w_old - learning_r ate * (1/n) * ∑ ∂Loss / ∂(loss_i) * ∂loss_i/∂w其中,learning_rate表示学习率,∂Loss / ∂(loss_i)和∂loss_i/∂w 分别表示前面计算得到的梯度部分。
4.梯度的传播在反向传播算法中,每个参数的梯度都会根据其对应的loss函数来计算,然后再通过网络的连接关系逐层向后传播。
多个loss损失反向传播的原理

多个loss损失反向传播的原理反向传播(Backpropagation)是深度学习中用于计算多个损失函数梯度的一种方法,它采用链式法则将损失函数的梯度反向传播到模型的每个参数上。
在深度学习中,通常会存在多个损失函数,每个损失函数对应不同的任务。
本文将主要介绍多个损失函数反向传播的原理。
1.多个损失函数的表达式在深度学习中,模型的输出通常由多个损失函数决定,每个损失函数可以看作是一个任务的指标。
设模型的输出为y,第i个损失函数为L_i(y),模型参数为θ。
则总损失函数可以表示为多个损失函数的加权和:L=Σα_i*L_i(y)其中,α_i是第i个损失函数的权重。
通过调整α_i的大小,可以对不同任务的影响程度进行调整。
2.损失函数对模型参数的偏导数为了将损失函数的梯度反向传播到模型参数上,首先需要计算损失函数对模型参数的偏导数。
设第i个损失函数L_i对模型输出y的偏导数为∂L_i/∂y,模型输出y对模型参数θ的偏导数为∂y/∂θ,则损失函数L对模型参数θ的偏导数可以由链式法则得到:∂L/∂θ=Σα_i(∂L_i/∂y)*(∂y/∂θ)其中,∂L_i/∂y可以由损失函数的具体形式求出,而∂y/∂θ可以由模型的前向传播过程和模型参数的定义求出。
3.梯度下降更新参数得到损失函数L对模型参数θ的偏导数后,就可以使用梯度下降算法更新模型参数。
梯度下降算法的更新规则为:θ_new = θ_old - η * ∂L / ∂θ其中,η是学习率。
4.权重的影响在计算总损失函数的梯度时,需要对各个任务的梯度进行加权求和。
具体来说,在计算损失函数L_i对模型输出y的偏导数∂L_i/∂y时,会乘以权重α_i。
通过调整权重α_i的大小,可以控制不同任务对总损失函数的影响程度。
5.梯度计算的传递和累加在多个损失函数反向传播的过程中,梯度的计算是从最后一个损失函数开始,逐步向前传递和累加的。
具体来说,对于第i个损失函数L_i,先计算∂L_i/∂y,然后将这个梯度乘以权重α_i,得到对应的损失函数梯度,再将这个梯度传递给模型的前一层进行计算,直到传递到模型的输入层。
bp使用方法

bp使用方法BP(反向传播算法)是一种用于训练神经网络的算法。
它通过反向传播误差来调整神经网络中的权重和偏差,以使其能够更好地逼近目标函数。
BP算法是一种有监督学习算法,它需要有标记的训练集作为输入,并且可以通过梯度下降法来最小化目标函数的误差。
BP算法的基本思想是在神经网络中,从输入层到输出层的正向传播过程中,通过计算网络的输出值与目标值之间的差异(即误差),然后将这个误差反向传播到网络的每一层,在每一层中调整权重和偏差,以最小化误差。
这个反向传播的过程将误差逐层传递,使得网络的每一层都能对误差进行一定程度的“贡献”,并根据这个贡献来调整自己的权重和偏差。
具体来说,BP算法可以分为以下几个步骤:1. 初始化网络:首先需要确定神经网络的结构,包括输入层、隐藏层和输出层的神经元个数,以及每层之间的连接权重和偏差。
这些权重和偏差可以初始化为随机值。
2. 前向传播:将输入样本送入网络,按照从输入层到输出层的顺序,逐层计算每个神经元的输出值。
具体计算的方法是将输入值和各个连接的权重相乘,然后将结果求和,并通过一个非线性激活函数(如Sigmoid函数)进行映射得到最终的输出值。
3. 计算误差:将网络的输出值与目标值进行比较,计算误差。
常用的误差函数有均方误差函数(Mean Squared Error,MSE)和交叉熵函数(Cross Entropy),可以根据具体问题选择合适的误差函数。
4. 反向传播:从输出层开始,根据误差对权重和偏差进行调整。
首先计算输出层神经元的误差,然后根据误差和激活函数的导数计算输出层的敏感度(即对权重的影响),并根据敏感度和学习率更新输出层的权重和偏差。
5. 更新隐藏层权重:同样地,根据输出层的敏感度,计算隐藏层的敏感度,并更新隐藏层的权重和偏差。
隐藏层的敏感度可以通过将输出层的敏感度按权重加权求和得到。
6. 重复步骤4和5:重复执行步骤4和5,将误差逐层传播,更新每一层的权重和偏差,直到达到训练的停止条件(如达到最大迭代次数或误差降至某个阈值)。
mlp 反向传播算法python代码

mlp 反向传播算法python代码在机器学习中,反向传播是一种常用的优化算法,用于训练神经网络。
在这篇文章中,我们将探讨反向传播算法的 Python 实现。
首先,让我们回顾一下反向传播的基本概念。
反向传播算法的目的是通过调整参数来最小化神经网络的误差。
该算法通过将误差信息在网络中向后传播,以计算每个参数对误差的贡献,并相应地更新参数。
反向传播的算法通常涉及以下步骤:1. 前向传播:网络将输入数据通过一系列变换传递,生成输出值。
2. 损失函数:损失函数与期望输出比较,生成误差。
3. 反向传播:误差反向传递回网络中,计算每个参数对误差的贡献。
4. 参数更新:将误差贡献信息用于更新网络中的参数。
下面是一个简单的 Python 函数,用于执行反向传播算法:```def backpropagation(X, Y, weights, bias, learning_rate):# 前向传播z = np.dot(X, weights) + biasexp_scores = np.exp(z)output = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)# 计算误差和梯度num_examples = X.shape[0]delta_output = outputdelta_output[range(num_examples), Y] -= 1d_weights = (1 / num_examples) * np.dot(X.T, delta_output)d_bias = (1 / num_examples) * np.sum(delta_output, axis=0, keepdims=True)# 更新参数weights -= learning_rate * d_weightsbias -= learning_rate * d_biasreturn weights, bias```该函数接收输入数据 X、期望输出 Y、权重 weights、偏差 bias 和学习率learning_rate。
BP(BackPropagation)反向传播神经网络介绍及公式推导
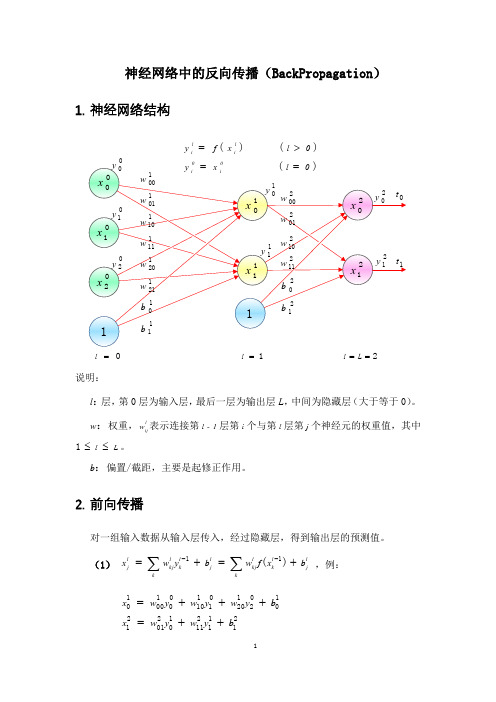
5. 链式法则
如果函数 u (t )及 v (t )都在 t 点可导,复合函数 z f(u,v)在对应点(u,v)具 有连续偏导数,z 在对应 t 点可导,则其导数可用下列公式计算:
dz z du z dv dt u dt v dt
6. 神经元误差
定义 l 层的第 i 个神经元上的误差为 il 即: (7)
5
附:激活函数
非线性: 当激活函数是线性的时候,一个两层的神经网络就可以逼近基 本上所有的函数了。但是,如果激活函数是恒等激活函数的时候(即 f(x)=x) ,就不满足这个性质了,而且如果 MLP 使用的是恒等激活函数, 那么其实整个网络跟单层神经网络是等价的。 可微性: 当优化方法是基于梯度的时候,这个性质是必须的。 单调性: 当激活函数是单调的时候,单层网络能够保证是凸函数。 f(x)≈x: 当激活函数满足这个性质的时候, 如果参数的初始化是 random 的很小的值, 那么神经网络的训练将会很高效; 如果不满足这个性质, 那 么就需要很用心的去设置初始值。 输出值的范围: 当激活函数输出值是 有限 的时候,基于梯度的优化方 法会更加 稳定,因为特征的表示受有限权值的影响更显著;当激活函数 的输出是 无限 的时候, 模型的训练会更加高效, 不过在这种情况小, 一 般需要更小的 learning rate.
l i
j
l 1 E x j x lj 1 xil
j
x lj 1 x
l i
jl 1 ,其中 l L
将公式(1) x j
l 1
w
k
l 1 l kj k
y blj 1
w
k
l 1 kj
f( xkl ) blj 1 ,对 x i 的求导
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯度下降和反向传播算法•引言 ————— 感知机与Delta法则•梯度下降算法•梯度下降概述•为什么梯度方向是上升最快的方向•梯度下降图解•梯度下降的一些问题•链式求导法则•反向传播算法•单个逻辑神经元的反向传播•多层全连接神经网络的反向传播•卷积神经网络的反向传播•梯度下降的优化算法引言 ————— 感知机与Delta法则•阈值与感知机法则:ii i i i x o t w w w w )(-=∆∆+←η t 是当前样例的目标输出,o 是感知机的输出, 是学习率.η•数据必须线性可分,特征选取是关键•收敛快,不容易推广为大型网络•线性单元与Delta法则∑-=→dd d o t w E 2)(21)(⎥⎦⎤⎢⎣⎡∂∂∂∂∂∂=∇-→110,,,)(n w E w E w E w E 损失函数的梯度:)(- ,→→→→→∇=∆∆+←w E w w w w η其中,∑∑∈∈-=∆--=∂∂Dd iddd iDd d d d i x ot wx o t w E)())((η•收敛慢,容易推广为大型网络梯度下降概述极值问题:• D 是domain, 函数的定义域, 是实数域.• D 是一维或者是高维的,.•每个维度的取值是离散的,或者连续的.•我们这里限制D 的每个维度都是连续的.•求解:ℜ→D f :)(argminx f xDx ∈*=nℜ⊆D 1. 随机搜索法尽量多的去尝试,从里面选择使得目标函数取值最小的参数.2. 随机局部搜索在现有的参数的基础上,搜寻一下周边临近的参数,若有更好的就更新参数,如此不断迭代. 3. 根据梯度选择方向搜索在现有的参数的基础上,计算函数梯度,按照梯度进行调参,如此不断迭代.ℜ为什么梯度方向上升最快?θθθθθθθθsin ),(cos ),( ),()sin ,()sin ,()sin ,cos (),()sin ,cos (0t ⋅∂∂+⋅∂∂=-+++-++=-++→yy x f x y x f ty x f t y x f t y x f t y t x f t y x f t y t x f •上升最快的方向即为方向导数最大的方向:上式即为向量在 上的投影.) ),( ,),( (yy x f x y x f ∂∂∂∂)sin ,(cos θθ2222),(),(),(sin,),(),(),(cos yy x f xy x f yy x f y y x f x y x f xy x f ∂∂+∂∂∂∂=∂∂+∂∂∂∂=θθ总之,)()()()1(i x i i x f xx∇-←+η•梯度下降算法核心迭代公式:走一步,看一步跑下去?(momentum)梯度下降图解梯度下降的一些问题•梯度为 0 的点成为 critical point•梯度下降迭代在梯度为0的点会终止运行,但是critical point 不一定是极值点•局部极小与全局极小•梯度下降不断逼近局部极小链式求导法则•粗略的讲,若 x 是实数,, )())((),(y f x g f z x g y===则dxdy dydz dxdz⋅=•粗略的讲,一般地,若)( ),( ,: ,: , ,y f z x g y f g y x nnmn m ==ℜ→ℜℜ→ℜℜ∈ℜ∈则ijjj ix y y z x z∂∂⋅∂∂=∂∂∑向量表达式为:zx y z y Tx ∇*⎪⎭⎫⎝⎛∂∂=∇其中,xy ∂∂m n ⨯是函数 的 Jacobian 矩阵.g单个逻辑神经元的反向传播)(),,(∑+==ii i b w x a x b W f σ)1( )(11)('σσσσ-⋅=+=-x e x x)1()()()(a a za a J z J a J a z a -=∂∂∂∂=∂∂=∂∂=δδδ•训练的最终目的是求 对参数 的偏导数•反向传播是从后往前一步步求偏导数J b W ,)()(z b Tz W bzz J b J J x W zz J W J J δδ=∂∂∂∂=∂∂=∇=∂∂∂∂=∂∂=∇①②③Jb b J W W b k k W k k ∇⋅-=∇⋅-=++ηη11激活函数表多层全连接网络的前向传播•神经网络实际上就是一个输入向量 到输出向量的函数,即:→x →y )(→→=x f y network 矩阵表示线性部分激活部分全部过程),( ) ( ) () (---11223112y a J a W a a W a a W a L L L L →--→→→→→⋅=⋅=⋅=σσσ456⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=→→→→→166362611553525114434241654165423211,,,,,,,,, , , 1 b b b w w w w w w w w w w w w w w w W z z z a x x x a )()(1122→→→⋅==a W z a σσ多层全连接神经网络的反向传播•第一层的是整个网络的输入,最后一层是损失函数的输入.1a L a •假设第层的输入和输出分别为:1+l 11,++l l a z )(111+++=+=l l lTll l z a b x W z σLa La J ∂∂=)(δ)1(1111++++-=∂∂l l l l a a z a I b z a W z W a z ll l l l l l l =∂∂=∂∂=∂∂+++111 , ,)1( )()()(111)(l l a l lll l z lz l T l ll l l a l a a z a a J z J W a z z J a J -=∂∂∂∂=∂∂==∂∂∂∂=∂∂=+++δδδδ)(111)(111z l ll l l b Tl z l l l l l W b z z J b J J a W z z J W J J ll++++++=∂∂∂∂=∂∂=∇=∂∂∂∂=∂∂=∇δδ卷积神经网络(Convolutional Neural Network -- CNN)•CNN的特征提取层参数是通过训练数据学习得到的,避免了人工特征抽取;•同一特征图的神经元共享权值,减少网络参数,这是卷积神经网络相对于全连接网络的一大优势.•CNN 基本层包括卷积层和池化层,二者通常一起使用,一个池化层紧跟在一个卷积层之后。
•这两层包括三个级联函数:卷积,激活函数函数,池化。
•其前向传播和后向传播的示意图如下:卷积神经网络的训练卷积层的训练——简单情形•卷积层前向传播公式:第 层第 j 行 第 j 列的误差项 filter 第 m 行 第 n 列权重 filter 的偏置项 第 层第 i 行 第 j 列神经元的输出 第层第 i 行 第 j 列神经元的加权输入第 层第 i 行 第 j 列的误差项 第 层的激活函数 1,-l j i δ1-l 1-l 1-l n m w ,l W l W bw 1,-l j i a 1,-l j i net l 1-l lji ,δ1-l f •先来考虑最简单的情况:步长为1,深度为1,filter 个数为1的情况.•根据链式求导法则,层神经元的误差为:1,1,1,1,1,-----∂∂⋅∂∂=∂∂=l j i l j i l j i l j i l j i net a a Enet E δ1-l1,12,22,11,21,22,12,21,112,11,12,12,11,112,12,12,112,11,11,112,11,11,111,11,11,111,1w w w w a E w w a net net E a net net E a E w a net net E a E ll l l l ll l l l l l l l ll l l l ⋅+⋅+⋅+⋅=∂∂⋅+⋅=∂∂⋅∂∂+∂∂⋅∂∂=∂∂⋅=∂∂⋅∂∂=∂∂------δδδδδδδ•先来看乘积的第一项:•上一页的计算,相当于把层的误差项矩阵周围补一圈0,再与旋转180度后的filter 进行卷积操作,简记此操作为 •其实,旋转180度之后进行现在的卷积,才是卷积的本来的含义:•写为求和的形式如下:l ∑∑++-=∂∂mnlnj m i l nm l ji wa E,,1,δflipconv =**•接着来看乘积的第2项:•根据链式求导法则,层神经元的误差为:1,1,1,1,1,-----∂∂⋅∂∂=∂∂=l j i l j i l j i l j i l ji net a a E net E δ1-l •第1项和第2项结合:•或写为如下表达式:卷积层神经元误差的训练——多步长•上面是步长为1时的卷积结果, 下面是步长为2时的卷积结果•当我们反向计算误差项时,先对第层的误差项相应的填充0, 再按照步长为的情形处理即可.l卷积层神经元误差的训练——输入层多深度•filter的深度和输入层的深度相同•各算各的,用filter的第d通道权重对第层误差项矩阵进行操作即可.卷积层神经元误差的训练——多 filter•filter 数量为 N 时,输出层即第层的深度也为 N •由于第 层的每个加权输入 都同时影响着第层所有 feature map 的输出,因此要用全导数反向计算误差;•我们使用每个filter 对第层相应的误差项矩阵进行 * 操作(翻转,卷积), 最后将所有结果按元素相加.l l 1-l 1, l j i net l卷积层 filter 权重的训练12,22,211,21,212,12,111,11,11,12,22,21,11,21,21,12,12,11,11,11,11,1----⋅+⋅+⋅+⋅=∂∂⋅∂∂+∂∂⋅∂∂+∂∂⋅∂∂+∂∂⋅∂∂=∂∂l l l l l l l l llll l l l l a a a a w net net Ew net net E w net net E w net net E w E δδδδ 13,22,212,21,213,12,112,11,12,1----⋅+⋅+⋅+⋅=∂∂l l l l l l l l a a a a w E δδδδ通式为:∑∑-++=∂∂mnl nj m i nm ji aw E1,,,δ卷积层 filter 权重的训练•filter 权重的更新操作即用第层的误差项矩阵作为卷积核,对第层的输出进行卷积.l1-l∑∑=+++=∂∂i jlj illllbwE,2,21,22,11,1δδδδδ•偏置项的梯度是第层误差项矩阵的逐项相加的结果:l•池化函数是一个下采样函数,对于大小为m 的池化区域,池化函数及其导数可以定义为:•均值池化: 导数:•最大值池化:导数:∑==mk kxmx g 11)(mx g i 1=∂∂iix x g max )(=Max Pooling Mean PoolingMaxPooling :•下一层的误差项的值原封不动的传递到上一层对应区块中最大值对应的神经元,•其他神经元的误差项的值都是0.MeanPooling :•下一层的误差项的值平均分配给上一层对应区块的每一个神经元梯度下降的优化算法随机梯度下降法(SGD )•每次只用一个样本进行前向传播,得到损失函数进行反向传播。
