高中数学求函数解析式经典精讲精练
高考求函数解析式方法及例题

高考求函数解析式方法及例题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN函数专题之解析式问题求函数解析式的方法把两个变量的函数关系,用一个等式来表示,这个等式叫函数的解析式,简称解析式。
求函数解析式的题型有:(1)已知函数类型,求函数的解析式:待定系数法;(2)已知()f x 求[()]f g x 或已知[()]f g x 求()f x :换元法、配凑法; (3)已知函数图像,求函数解析式;(4)()f x 满足某个等式,这个等式除()f x 外还有其他未知量,需构造另个等式:解方程组法;(5)应用题求函数解析式常用方法有待定系数法等。
,求f(x)的解,待定系数法()f x 22(2)f x -=(2)f x --设二次函数满足且图象在轴上的截距为1,在轴截得的线段长为,求的解析式。
x y ()f x 例题:解法一、1222x x a∆-==2248b ac a ∴-=21()212f x x x ∴=++1c =又1,2,12a b c ===解得2()(0)f x ax bx c a =++≠设(2)(2)f x f x -=--由40a b -=得解法二、(0)1f =41a k ∴+=1222x x -=222k a-∴=1,12a k ∴==-221()(2)121212f x x x x ∴=+-=++()y f x =2x =-得的对称轴为(2)(2)f x f x -=--由∴2()(2)f x a x k=++设二 【换元法】(注意新元的取值范围)已知))((x g f 的表达式,欲求)(x f ,我们常设)(x g t =,从而求得)(1t g x -=,然后代入))((x g f 的表达式,从而得到)(t f 的表达式,即为)(x f 的表达式。
三【配凑法(整体代换法)】若已知))((x g f 的表达式,欲求)(x f 的表达式,用换元法有困难时,(如)(x g 不存在反函数)可把)(x g 看成一个整体,把右边变为由)(x g 组成的式子,再换元求出)(x f 的式子。
函数图象的变换(原卷版)高中数学函数精讲精练 专题38

专题38函数图象的变换主要考查:函数图象的变换一、单选题1.已知指数函数()xf x a =,将函数()f x 的图象上的每个点的横坐标不变,纵坐标扩大为原来的3倍,得到函数()g x 的图象,再将()g x 的图象向右平移2个单位长度,所得图象恰好与函数()f x 的图象重合,则a 的值是()A .32B .23C .33D .32.函数()f x 的图象向左平移2个单位,所得图象与lg y x =的图象关于x 轴对称,则()f x =()A .()12g x --B .()12g x -C .()12g x -+D .()12g x +3.把函数2(2)2y x =-+的图象向左平移1个单位长度,再向上平移1个单位长度,所得图象对应的函数解析式是()A .2(3)3y x =-+B .2(3)1y x =-+C .2(1)3y x =-+D .2(1)1y x =-+4.已知函数3()log f x x =,将函数()y f x =的图象向右平移1个单位长度,再将所得的函数图象上的点的横坐标缩短为原来的12,纵坐标不变,然后将所得的图象上的点的纵坐标伸长为原来的3倍,横坐标不变,得到函数()y g x =的图象,则函数()g x 的解析式为()A .31()3log 12g x x ⎛⎫=-⎪⎝⎭B .3111()log 322g x x ⎛⎫=- ⎪⎝⎭C .3()3log (21)g x x =-D .3()3log (22)g x x =-5.已知函数()ln ,0,0xx x x f x x x e ⋅>⎧⎪=⎨≤⎪⎩,则函数(1)y f x =--的部分图象大致为()A .B .C .D .6.在平面直角坐标系中,先将抛物线223y x x =+-关于原点作中心对称变换,再将所得的抛物线关于y轴作轴对称变换,那么经过两次变换后所得的新抛物线的解析式为()A .223y x x =-+-B .2y x 2x 3=-++C .223y x x =--+D .223y x x =++7.将曲线2log y x =沿x 轴正方向移动1个单位长度,再沿y 轴负方向移动2个单位长度,得到曲线C ,在下列曲线中,与C 关于直线0x y +=对称的曲线方程是().A .221x y +=-B .221x y +=--C .221x y -=--D .221x y -=-8.如果两个方程的曲线经过若干次平移或对称变换后能够完全重合,则称这两个方程为“互为镜像方程对”,给出下列四对方程:①sin y x =与πcos 5y x ⎛⎫=+⎪⎝⎭②2ln y x =与2ln y x =③24x y =与24y x =④3y x =与32332y x x x =-++则“互为镜像方程对”的是()A .①②③B .①③④C .②③④D .①②③④二、多选题9.为了得到函数ln()y ex =的图象,可将函数ln y x =的图象()A .纵坐标不变,横坐标伸长为原来的e 倍B .纵坐标不变,横坐标缩短为原来的1eC .向上平移一个单位长度D .向下平移一个单位长度10.定义:在平面直角坐标系xOy 中,若存在常数()0ϕϕ>,使得函数()y f x =的图象向右..平移ϕ个单位长度后,恰与函数()y g x =的图象重合,则称函数()y f x =是函数()y g x =的“原形函数”.下列四个选项中,函数()y f x =是函数()y g x =的“原形函数”的是()A .()2f x x =,()221g x x x =-+B .()sin f x x =,()cos g x x =C .()ln f x x =,()ln2xg x =D .()13xf x ⎛⎫= ⎪⎝⎭,()123xg x ⎛⎫= ⎪⎝⎭11.由函数()3x f x =的图象得到函数2()3x g x +=的图象,正确的变换方法有()A .将()f x 的图象向左平移2个单位长度B .将()f x 的图象上各点的纵坐标伸长到原来的9倍C .先将()f x 的图象上各点的纵坐标伸长到原来的3倍,再向左平移1个单位长度D .先将()f x 的图象向右平移1个单位长度,将各点的纵坐标伸长到原来的3倍12.下列关于函数213()log (22)f x x x =-+的结论中,正确的有()A .值域为(,0]-∞B .在区间(1,)+∞上单调递增C .图象关于直线1x =对称D .把23()log (1)g x x =+的图象先向右平移1个单位;再关于x 对称,可得()f x 的图象.三、填空题13.函数()y f x =的图象向右平移1个单位长度,所得图象与函数xy e =的图象关于y 轴对称,则()f x =________14.将函数12log y x =的图象沿x 轴向右平移1个单位,得到图象C ,图象C 1与C 关于原点对称,图象C 2与C 1关于直线y x =对称,则C 2对应的函数解析式为______________.15.将函数2log y x =的图象上每一点的纵坐标不变,横坐标变为原来的(0)m m >倍,得到图象C ,若将2log y x =的图象向上平移2个单位,也得到图象C ,则m =__________.16.已知函数()1f x 2x⎛⎫= ⎪⎝⎭的图象与函数y=g(x)的图象关于直线y=x 对称,令h(x)=g(1-|x|),则关于h(x)有下列命题:①h(x)的图象关于原点对称;②h(x)为偶函数;③h(x)的最小值为0;④h(x)在(0,1)上为减函数.其中正确命题的序号为_________.(将你认为正确的命题的序号都填上)四、解答题17.利用指数函数()2x y f x ==的图象,作出下列各函数的图象:(1)(1)=-y f x ;(2)(||)y f x =;(3)()1y f x =-;(4)()y f x =-;(5)|()1|y f x =-;(6)()y f x =--.18.已知函数2()log (1)=+f x x ,将()y f x =的图象向左平移1个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数()y g x =的图象.(1)求()y g x =的解析式及定义域;(2)求函数()()()F x f x g x =-的最大值.19.已知函数()g x 的图象由2()f x x =向右平移一个单位,再向下平移一个单位得到.(1)求()g x 的解析式,并求函数()2g x y =的最小值.(2)解方程lg[()]lg[2()3]g x f x =-.20.已知函数(32)1x f x -=-([0,2])x ∈,将函数()y f x =的图象向右平移2个单位,再向上平移3个单位可得函数()y g x =的图象.(1)求函数()y f x =与()y g x =的解析式;(2)设22()[()]()h x g x g x =+,试求函数()y h x =的最值.21.已知函数()f x 的图象向右平移2个单位长度得到函数()2log 2y x =-的图象.(1)求()f x 的解析式;(2)若函数()()()227g x f x f x =-+⎡⎤⎣⎦,求()g x 在1,42⎡⎤⎢⎥⎣⎦上的最大值和最小值的和.22.已知0a >,将函数()212f x ax a =-的图象向右平移1a 个单位长度,再向下平移12a个单位长度后,得到函数()g x 的图象.(1)求函数()g x 的表达式;(2)当12a =时,求()g x 在区间[]4,3-上的最大值和最小值;(3)若函数()g x 在2,2⎤⎦上的最小值为()h a ,求()h a 的最大值.。
求函数解析式的方法和例题

求函数解析式的方法和例题一、常见的函数解析式的求法。
1. 一次函数,一次函数的一般形式为y=ax+b,其中a和b为常数,通过两点法、斜率法、解方程法等可以求得一次函数的解析式。
2. 二次函数,二次函数的一般形式为y=ax^2+bx+c,其中a、b、c为常数且a≠0。
通过配方法、求顶点法、根的性质等方法可以求得二次函数的解析式。
3. 指数函数,指数函数的一般形式为y=a^x,其中a为常数且a>0且a≠1。
通过观察法、对数法、取对数法等方法可以求得指数函数的解析式。
4. 对数函数,对数函数的一般形式为y=loga(x),其中a为常数且a>0且a≠1。
通过观察法、指数法、换底公式等方法可以求得对数函数的解析式。
5. 三角函数,三角函数包括正弦函数、余弦函数、正切函数等,它们的解析式可以通过周期性、对称性、变换公式等方法求得。
二、函数解析式的例题。
1. 求一次函数y=2x+3的解析式。
解,由于一次函数的一般形式为y=ax+b,所以y=2x+3的解析式为y=2x+3。
2. 求二次函数y=x^2+3x-2的解析式。
解,通过配方法或求顶点法可以求得y=x^2+3x-2的解析式为y=(x+2)(x-1)。
3. 求指数函数y=2^x的解析式。
解,观察法可得y=2^x的解析式为y=2^x。
4. 求对数函数y=log2(x)的解析式。
解,换底公式可得y=log2(x)的解析式为y=log(x)/log(2)。
5. 求正弦函数y=sin(x)的解析式。
解,通过周期性和对称性可得y=sin(x)的解析式为y=sin(x)。
以上就是关于求函数解析式的方法和例题的介绍,希望对大家有所帮助。
在学习过程中,要灵活运用各种方法,多加练习,提高解析式求解的能力。
5.7 三角函数的应用(精练)(原卷版)-人教版高中数学精讲精练(必修一)

7.(2022·湖南·高一课时练习)如图为某简谐振动的图象,它符合 y Asin ωx φ( A 0 , 0 , )
2
2
的形式.
(1)求该简谐振动的振幅、周期、频率和初相; (2)求该简谐振动的函数解析式; (3)求该函数的单调递增区间.
8.(2021·全国·高一专题练习)用弹簧挂着的小球做上下运动,它在 t 秒时相对于平衡位置的高度 h 厘米由
5.7 三角函数的应用(精练)
1 在几何中的应用
1.(2022 广东)如图,在扇形 POQ 中,半径 OP 2 ,圆心角 POQ ,B 是扇形弧上的动点,矩形 ABCD 3
内接于扇形.其中 CD 在半径 OQ 上,记 BOC .
(1)当 BOC 45 时,求矩形 ABCD 的面积; (2)求当角 取何值时,矩形 ABCD 的面积最大?并求出这个最大值.
答下列问题:
(1)单摆运动的周期是多少? (2)从 O 点算起,到曲线上的哪一点表示完成了一次往复运动?如从 A 点算起呢? (3)当 t 11s 时,单摆小球相对于静止位置的位移是多少? 6(2022·河南·高一阶段练习)如图,某个弹簧振子(简称振子)在完成一次全振动的过程中,时间 t(单位: s )与位移 y (单位: mm )之间的对应数据如表所示,其变化规律可以用
下列关系式确定:
h
2
sin
t
4
.以
t
为横坐标,h
为纵坐标,作出这个函数在
0,
2
上的图象,并回答
下列问题.
(1)小球在开始振动时(即 t 0 时)的位置在哪里? (2)小球的最高点和最低点与平衡位置的距离分别是多少? (3)经过多长时间小球往复运动一次? (4)每秒钟小球能往复运动多少次?
函数的解析式(原卷版)高中数学函数精讲精练 专题08

专题08函数的解析式主要考查:换元法,配凑法,待定系数法,方程组法求函数的解析式一、单选题1.已知函数()2123f x x x -=+-,则()f x =()A .24x x +B .24x +C .246x x +-D .241x x --2.已知函数()f x 满足()cos 1cos 21f x x -=-,则()f x 的解析式为()A .()()22420f x x x x =+-≤≤B .()()224f x x x x R =+∈C .()()2120f x x x =--≤≤D .()()21f x x x R =-∈3.若()2x x e f x e =+,则()f x 的表达式为()A .()()2ln f x x x x R =+∈B .()()2ln 0f x x x x =+>C .()()2ln f x x x x R =+∈D .()()2ln 0f x x x x =+>4.已知)1f x =+,则函数()f x 的解析式为()A .()()210f x x x =-≥B .()()211f x x x =-≥C .()()20f x x x =≥D .()()21f x x x =≥5.已知()f x 是一次函数,且(())41f f x x =-,则()f x 的解析式为()A .1()23f x x =-或()21f x x =-+B .()21f x x =+或()21f x x =--C .()21f x x =-或1()23f x x =-+D .()21f x x =+或()21f x x =-6.已知()f x 是二次函数,且(0)1f =-,(1)()22f x f x x +=-+,则()f x 的解析式为()A .2()31f x x x =-+-B .23()12f x x x =---C .213()222f x x x =-+D .21()222f x x x =-+7.若()f x 对于任意实数x 恒有()()231f x f x x --=+,则()f x =()A .x -1B .x +1C .2x +1D .3x +38.已知函数()f x 的定义域为()0,∞+,且()121f x f x ⎛⎫=⎪⎝⎭,则()f x =()A()203x +>B()103x >C.()10x +>D()10x >二、多选题9.已知函数()f x 是一次函数,满足(())98f f x x =+,则()f x 的解析式可能为()A .()32f x x =+B .()32f x x =-C .()32f x x =-+D .()34f x x =--10.若函数()()221120x f x x x--=≠,则下列结论正确的是()A .1152f ⎛⎫= ⎪⎝⎭B .()324f =-C .()241(0)(1)f x x x =-≠-D .()221411x f x x ⎛⎫=- ⎪⎝⎭-(0x ≠且1x ≠)11.已知()f x 满足()2(-)21f x f x x -=-,则()A .(3)3f =B .(3)3f =-C .()()2f x f x +-=D .()()-2f x f x +-=12.具有性质:()1f f x x ⎛⎫=-⎪⎝⎭的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是()A .()1f x x x =-B .()1f x x x=+C .(),010,11,1x x f x x x x ⎧⎪<<⎪==⎨⎪⎪->⎩D .(),010,11,1x x f x x x x⎧⎪<<⎪==⎨⎪⎪>⎩三、填空题13.设()2f x x a =+,()21()34g x x =+,且()()21g f x x x =-+,则a 的值为________.14.已知1x f x +⎛⎫ ⎪⎝⎭=221x x++1x ,则f (x )的解析式为________.15.已知2211f x x x x ⎛⎫-=+ ⎪⎝⎭,则函数(3)f =______.16.已知()f x 是定义域为R 的单调函数,且对任意实数x ,都有()32415x f f x ⎡⎤+=⎢⎥+⎣⎦,则217log sin 6f π⎛⎫= ⎪⎝⎭______.四、解答题17.已知()f x 满足()1212x f x f x x ⎛⎫+-=+ ⎪+⎝⎭,求函数()f x 的解析式.18.根据条件,求函数解析式()f x .(1)()2132f x x x +=-+;(2))223f x -=+;(3)2211f x x x x ⎛⎫+=+ ⎪⎝⎭;(4)已知()f x 是一元二次函数,且满足()00f =;()()11f x f x x +=++.19.(1)已知2(1)23f x x x +=-+,求()f x .(2)已知()49f f x x =+⎡⎤⎣⎦,且()f x 为一次函数,求()f x .(3)已知函数()f x 满足12()f x f x x ⎛⎫+= ⎪⎝⎭,求()f x .20.根据下列条件,求函数()f x 的解析式;(1)已知()f x 是一次函数,且满足()()3121217f x f x x +--=+;(2)已知3311f x x x x ⎛⎫+=+ ⎪⎝⎭;(3)已知等式()()()21f x y f x y x y -=--+对一切实数x 、y 都成立,且()01f =;(4)函数()f x 满足条件()123f x f x x ⎛⎫+= ⎪⎝⎭对任意不为零的实数x 恒成立21.已知定义域为R 的函数()f x 和()g x ,其中()f x 是奇函数,()g x 是偶函数,且1()()2x f x g x ++=.(1)求函数()f x 和()g x 的解析式;(2)解不等式:2()()f x g x ≥;(3)若关于x 的方程()()10f x g x λ-+=有实根,求正实数...λ的取值范围.22.在①2(23)46f x x x -=-,②2()2()33f x f x x x +-=-,③对任意实数x ,y ,均有+=22f x y f y()2()++-+-这三个条件中任选一个,补充在下面问题中并解答.已知函数x xy y x y233()f x的解析式.注:如果选择多个条件解答,按第一个解答计分.f x满足_________,求()。
高中数学求函数解析式解题方法大全与配套练习
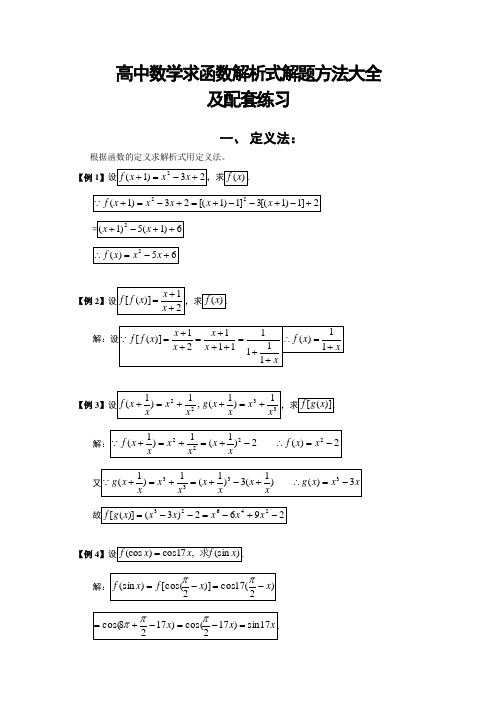
高中数学求函数解析式解题方法大全及配套练习一、定义法:根据函数的定义求解析式用定义法。
【例1】【例2】【例3】【例4】二、待定系数法:(主要用于二次函数)已知函数解析式的类型,可设其解析式的形式,根据已知条件建立关于待定系数的方程,从而求出函数解析式。
它适用于已知所求函数类型(如一次函数,二次函数,正、反例函数等)及函数的某些特征求其解析式的题目。
其方法:已知所求函数类型,可预先设出所求函数的解析式,再根据题意列出方程组求出系数。
【例1】【解析】【例2】已知二次函数f(x)满足f(0)=0,f(x+1)= f(x)+2x+8,求f(x)的解析式.解:设二次函数f(x)= ax2+bx+c,则f(0)= c= 0 ①f(x+1)(x+1)= ax2+(2a+b)x+a+b②由f(x+1)= f(x)+2x+8 与①、②得解得故f(x)= x2+7x.【例3】三、换元(或代换)法:道所求函数的类型,且函数的变量易于用另一个变量表示的问题。
使用换元法时要注意新元定义域的变化,最后结果要注明所求函数的定义域。
如:已知复合函数f [g(x)]的解析式,求原函数f(x)的解析式,把g(x)看成一个整体t,进行换元,从而求出f(x)的方法。
实施换元后,应注意新变量的取值围,即为函数的定义域.【例1】【解析】【例2】【例3】【例4】(1)在(1(2)1(3)【例5】(1(2)由【例6】四、代入法:求已知函数关于某点或者某条直线的对称函数时,一般用代入法.【例1】解则解得,上,(五)配凑法【例1】:2x当然,上例也可直接使用换元法即由此可知,求函数解析式时,可以用配凑法来解决的,有些也可直接用换元法来求解。
【例2】:分析:此题直接用换元法比较繁锁,而且不易求出来,但用配凑法比较方便。
实质上,配凑法也缊含换元的思想,只是不是首先换元,而是先把函数表达式配凑成用此复合函数的函数来表示出来,在通过整体换元。
和换元法一样,最后结果要注明定义域。
高考数学高频考点《求函数的解析式》

高频考点之求函数的解析式1. 设)(x f 是一次函数,且34)]([+=x x f f ,则)(x f =2.已知二次函数)(x f 满足(1)1f =,(1)5f -=,图像过原点,求()f x 的解析式3. 已知()f x 是二次函数,若(0)0,f =且(1)()1f x f x x +=++ 求()f x 的解析式。
4. 已知1)1,f x =+求()f x 的解析式。
5. 已知()21252f x x x +=++,求()f x 的解析式6 .里氏震级M 的计算公式为0lg lg A A M -=,其中A 是测震仪记录的地震曲线的最大振幅,0A 是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振福是1000,此时标准地震的振幅0A 为0.001,则此次地震的震级为 级;9级地震的最大的振幅是5级地震最大振幅的 倍.7. 渔场中鱼群的最大养殖量是m吨,为保证鱼群的生长空间,实际养殖量不能达到最大养殖量,必须留出适当的空闲量。
已知鱼群的年增长量y吨和实际养殖量x吨与空闲率乘积成正比,比例系数为k(k>0).(1)写出y关于x的函数关系式,指出这个函数的定义域;(2)求鱼群年增长量的最大值;(3)当鱼群的年增长量达到最大值时,求k的取值范围.8 .某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿的市场售价P(单位:元/102 kg)与上市时间t(单位:天)的关系符合图1中的折线表示的函数关系,西红柿种植成本Q(单位:元/102 kg)与上市时间t(单位:天)的关系符合图2中的抛物线表示的函数关系.(1)写出图1表示的西红柿的市场售价与上市时间的函数关系式P=f(t),图2表示的西红柿的种植成本与上市时间的函数关系式Q=g(t);(2)若西红柿的市场售价减去其种植成本为西红柿的纯收益,则何时上市西红柿的纯收益最大?9 某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.(1)写出服药后y 与t 之间的函数关系式)(t f y ;(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗疾病有效.求服药一次治疗疾病有效的时间?。
高中数学求函数解析式经典精讲精练

求函数解析式常用的方法 (一)待定系数法它适用于已知所求函数类型(如一次函数,二次函数,正、反例函数等)及函数的某些特征求其解析式的题目。
其方法:已知所求函数类型,可预先设出所求函数的解析式,再根据题意列出方程组求出系数。
例1:已知()f x 是二次函数,若(0)0,f =且(1)()1f x f x x +=++试求()f x 的表达式。
解析:设2()f x ax bx c =++ (a ≠0),由(0)0,f =得c=0,由(1)()1f x f x x +=++得,22(1)(1)1a xb xc ax bx c x ++++=++++,整理得22(2)()1ax a b x a b c ax b c x c +++++=++++得 212211120011()22a ab b a bc c b c c f x x x⎧=⎪+=+⎧⎪⎪⎪++=+⇒=⎨⎨⎪⎪=⎩=⎪⎪⎩∴=+ 小结:我们只要明确所求函数解析式的类型,便可设出其函数解析式,设法求出其系数即可得到结果。
类似的已知f(x)为一次函数时,可设f(x)=ax+b(a ≠0);f(x)为反比例函数时,可设f(x)=kx(k ≠0);f(x)为二次函数时,根据条件可设 ①一般式:f(x)=ax2+bx+c(a ≠0)②顶点式:f(x)=a(x-h)2+k(a ≠0)③双根式:f(x)=a(x-x1)(x-x2)(a ≠0)例1 设)(x f 是一次函数,且34)]([+=x x f f ,求)(x f解:设b ax x f +=)( )0(≠a ,则b ab x a b b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 (二)换元法用来处理不知道所求函数的类型,且函数的变量易于用另一个变量表示的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求函数解析式常用的方法(一) 待定系数法它适用于已知所求函数类型(如一次函数,二次函数,正、反例函数等)及函数的某些特征求其解析式的题目。
其方法:已知所求函数类型,可预先设出所求函数的解析式,再根据题意列出方程组求出系数。
例1:已知()f x 是二次函数,若(0)0,f =且(1)()1f x f x x +=++试求()f x 的表达式。
解析:设2()f x ax bx c =++ (a ≠0),由(0)0,f =得c=0,由(1)()1f x f x x +=++ 得,22(1)(1)1a x b x c ax bx c x ++++=++++,整理得22(2)()1ax a b x a b c ax b c x c +++++=++++得 212211120011()22a ab b a bc c b c c f x x x⎧=⎪+=+⎧⎪⎪⎪++=+⇒=⎨⎨⎪⎪=⎩=⎪⎪⎩∴=+小结:我们只要明确所求函数解析式的类型,便可设出其函数解析式,设法求出其系数即可得到结果。
类似的已知f(x)为一次函数时,可设f(x)=ax+b(a≠0);f(x)为反比例函数时,可设f(x)=kx(k≠0);f(x)为二次函数时,根据条件可设 ①一般式:f(x)=ax2+bx+c(a≠0)②顶点式:f(x)=a(x-h)2+k(a≠0)③双根式:f(x)=a(x-x1)(x-x2)(a≠0) 例1 设)(x f 是一次函数,且34)]([+=x x f f ,求)(x f解:设b ax x f +=)()0(≠a ,则b ab x ab b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 (二)换元法用来处理不知道所求函数的类型,且函数的变量易于用另一个变量表示的问题。
它主要适用于已知复合函数的解析式,但使用换元法时要注意新元定义域的变化,最后结果要注明所求函数的定义域。
例2:已知1)1,f x =+求()f x 的解析式。
1视为t ,那左边就是一个关于t 的函数()f t ,1t =中,用t 表示x ,将右边化为t 的表达式,问题即可解决。
1t =22201()(1)2(1)1()(1)x t f t t t t f x x x ≥∴≥∴=-+-+=∴=≥ 小结:①已知f[g(x)]是关于x 的函数,即f[g(x)]=F(x),求f(x)的解析式,通常令g(x)=t ,由此能解出x=(t),将x=(t)代入f[g(x)]=F(x)中,求得f(t)的解析式,再用x 替换t ,便得f(x)的解析式。
注意:换元后要确定新元t 的取值范围。
(三)配凑法已知复合函数[()]f g x 的表达式,要求()f x 的解析式时,若[()]f g x 表达式右边易配成()g x 的运算形式,则可用配凑法,使用配凑法时,要注意定义域的变化。
例3:已知1)f x =+求()f x 的解析式。
分析:2x x +可配凑成∴可用配凑法,解:由21))1f x =+=-,令t =,01x t ≥∴≥则2()1f t t =-, 即2()1(1)f x x x =-≥,当然,上例也可直接使用换元法,令t =1t =得222(1)()(1)2(1)1x t f t t t t =-∴=-+-=-,即2()1(1)f x x x =-≥,由此可知,求函数解析式时,可以用配凑法来解决的,有些也可直接用换元法来求解。
例4:已知2211(),f x x x x-=+求()f x .解析:由222111()()2f x x x x x x -=+=-+,令2110t x x tx x=-⇒--=,由0∆≥即240t+≥得t R ∈2()2f t t ∴=+即:2()2()f x x x R =+∈实质上,配凑法和换元法一样,最后结果要注明定义域。
例2 已知221)1(x x x x f +=+ )0(>x ,求 ()f x 的解析式解:2)1()1(2-+=+xx x x f , 21≥+x x 2)(2-=∴x x f )2(≥x(四)消元法,此方法的实质是解函数方程组。
条件中,有若干复合函数与原函数()f x 混合运算,则要充分利用变量代换,然后联立方程组消去其余部分。
例5:设()f x 满足1()2(),f x f x x -=求()f x 的解析式。
分析:要求()f x 可消去1()f x ,为此,可根据题中的条件再找一个关于()f x 与1()f x的等式,通过解方程组达到消元的目的。
解析:1()2()f x f x x-=①,显然,0x ≠,将x 换成1x 得11()2()f f x x x -=②由1()2()11()2()f x f x x f f x xx ⎧-=⎪⎪⎨⎪-=⎪⎩ 消去1()f x ,得12()33f x x x=-- 例6 设)(x f 为偶函数,)(x g 为奇函数,又,11)()(-=+x x g x f 试求)()(x g x f 和的解析式 解 )()(),()(x g x g x f x f -=-=-∴,又11)()(-=+x x g x f ① ,用x -替换x 得:11)()(+-=-+-x x g x f ,即11)()(+-=-x x g x f ② ,解① ②联立的方程组,得11)(2-=x x f ,x x x g -=21)( 小结:消元法适用于自变量的对称规律。
互为倒数,如f(x)、1()f x;互为相反数,如f(x)、f(-x),通过对称代换构造一个对称方程组,解方程组即得f(x)的解析式。
(五)赋值法其方法:将适当变量取特殊值,使问题具体化、简单化,依据结构特点,从而找出一般规律,求出解析式。
例5:已知(0)1,()()(21),f f a b f a b a b =-=--+求()f x 。
解析:令0,a =则2()(0)(1)1f b f b b b b -=--=-+ 令b x -=则2()1f x x x =++小结:①所给函数方程含有2个变量时,可对这2个变量交替用特殊值代入,或使这2个变量相等代入,再用已知条件,可求出未知的函数,至于取什么特殊值,根据题目特征而定。
②通过取某些特殊值代入题设中等式,可使问题具体化、简单化,从而顺利地找出规律,求出函数的解析式。
六、代入法:求已知函数关于某点或者某条直线的对称函数时,一般用代入法。
例4已知:函数)(2x g y x x y =+=与的图象关于点)3,2(-对称,求)(x g 的解析式解:设),(y x M 为)(x g y =上任一点,且),(y x M '''为),(y x M 关于点)3,2(-的对称点 则⎪⎩⎪⎨⎧=+'-=+'3222y y xx ,解得:⎩⎨⎧-='--='y y x x 64 , 点),(y x M '''在)(x g y =上,x x y '+'='∴2,把⎩⎨⎧-='--='yy x x 64代入得: )4()4(62--+--=-x x y ,整理得672---=x x y ,∴67)(2---=x x x g七、递推法:若题中所给条件含有某种递进关系,则可以递推得出系列关系式,然后通过迭加、迭乘或者迭代等运算求得函数解析式。
例8 设)(x f 是定义在+N 上的函数,满足1)1(=f ,对任意的自然数b a , 都有ab b a f b f a f -+=+)()()(,求)(x f解 +∈-+=+N b a ab b a f b f a f ,)()()(,,∴不妨令1,==b x a ,得:x x f f x f -+=+)1()1()(,又1)()1(,1)1(+=-+=x x f x f f 故 ①分别令①式中的1,21x n =- 得:(2)(1)2,(3)(2)3,()(1),f f f f f n f n n -=-=--=,将上述各式相加得:n f n f ++=-32)1()(, 2)1(321)(+=+++=∴n n n n f +∈+=∴N x x x x f ,2121)(2五、待定系数法例5. 已知二次函数)x (f 的二次项系数为a ,且不等式x 2)x (f ->的解集为(1,3),方程0a 6)x (f =+有两个相等的实根,求)x (f 的解析式。
解:因为的0x 2)x (f >+解集为(1,3),设0a ),3x )(1x (a x 2)x (f <--=+且,所以x 2)3x )(1x (a )x (f ---=a 3x )a 42(ax 2++-= ①,由方程0a 6)x (f =+,得0a 9x )a 42(ax 2=++- ②,因为方程②有两个相等的实根,所以0a 9a 4)]a 42([2=⋅-+-=∆,即,01a 4a 52=--解得51a 1a -==或,又51a ,0a -=<所以,将51a -=①得53x 56x 51)x (f 2---=。
六、函数性质法利用函数的性质如奇偶性、单调性、周期性等求函数解析式的方法。
例6. 已知函数)x (f y =是R 上的奇函数,当)x (f ,13)x (f ,0x x求时-=≥的解析式。
解析:因为)x (f 是R 上的奇函数,所以)x (f )x (f ),x (f )x (f --=-=-即,当0x ,0x >-<时,13)13()x (f )x (f xx +-=--=--=--,所以⎪⎩⎪⎨⎧<+-≥-=-0x ,130x ,13)x (f xx七、反函数法利用反函数的定义求反函数的解析式的方法。
例7. 已知函数)0x (1x ln y >+=,求它的反函数。
解:因为0x >,1y ex ,1y x ln ,1x ln y R1x ln y -=-=+=∈+=∴所以得由∴反函数为)R x (ey 1x ∈=-八、“即时定义”法给出一个“即时定义”函数,根据这个定义求函数解析式的方法。
例8. 对定义域分别是g f D D 、的函数)x (g y ),x (f y ==,规定:函数⎪⎪⎩⎪⎪⎨⎧∈∉∉∈∈∈⋅=g f g f g f d x D x ),x (g ,D x D x ),x (f D x D x ),x (g )x (f )x (h 且当且当且当若2x )x (g ,1x 1)x (f =-=,写出函数)x (h 的解析式。
