年高考数学专题02高考考前调研卷二-2019最新整理
深圳市2019年高三年级第二次调研考试数学(理科)试题(含答案)

学 (1)求 ABC 的大小;
(2)求△ ABC 的面积.
科 解:(1)(法一)依题意设 ABD = 2CBD = 2 ,
∵ AD = 2CD , AC = 2 5 ,
∴ AD = 4 5 , CD = 2 5 ,
育3
3
…………………………………………2 分
在△ BAD 中,由正弦定理,可得 AB = AD ,
Sn
Sn−1
令 bn
=
2n S
+
n
1
,则
bn
− bn−1
=
2(n
2 ),
数列{bn}是以 b1
=
3 S1
=
3 a1
= 1为首项,公差 d
=
2 的等差数列,
bn
=
2n
−1,即
2n +1 Sn
=
2n
−1 ,
Sn
=
2n +1 2n −1
,
S1S2
Sm
=
3
5 3
2m 2m
+1 −1
=
2m
+1
,
由 2m +1 2019 ,解得 m 1009 ,即正整数 m 的最小值为1009 ,故应填1009 .
三、解答题:解答应写出文字说明,证明过程或演算步骤.
理科数学试题答案及评分参考第2页(共13页)
市教育科
院
17.(本小题满分 12 分)
究
研 已知△ ABC 中,AB = 2BC ,AC = 2 5 ,点 D 在边 AC 上,且 AD = 2CD ,ABD = 2CBD .
教 sin ADB sin ABD
2019届高三入学调研考试卷文科数学(二)含答案
平均气温(℃)
2
3
5
6
销售额(万元)
20
23
27
30
根据以上数据,求得 y 与 x 之间的线性回归方程 y b x a 的系数 b 则 a ________.
12 ,
5
15.已知某三棱柱的三视图如图所示, 那么该三棱柱最大侧面的面积为 __________.
16.如图为函数 f x Asin 2 x
A. 2 3
B.2
C. 3
D.1
6.已知函数 f x 2sin x ,
0,0
的部. 1,3 4
B . 2, 4
C. 3 4
D. 2 4
7.若过点
2,0 有两条直线与圆
2
x
2
y 2x 2y
m 1 0 相切, 则实数 m 的取值
范围是(
)
A. , 1
B . 1,+
C. 1,0
(A 0,
x2 a,b ,若 f x1 f x2 ,都有 f x1 x2
) 的部分图象,对于任意的 2
x1 ,
2 ,则 等于 __________.
三、解答题(本大题有 6 小题,共 70 分.解答应写出文字说明、证明过 程或演算步骤)
C. 1,1
2. i 为虚数单位,复数 z 2i 在复平面内对应的点所在象限为( i1
A .第二象限
B .第一象限
C .第四象限
D . 1,2 )
D .第三象限
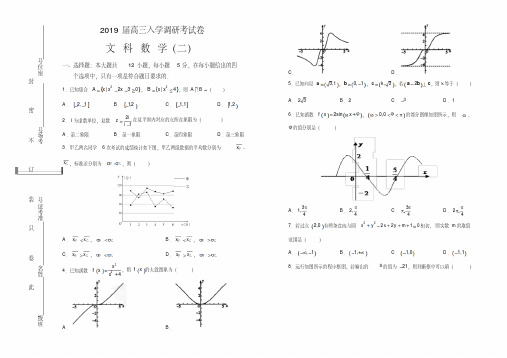
3.甲乙两名同学 6 次考试的成绩统计如下图,甲乙两组数据的平均数分别为
x甲 、
x乙 ,标准差分别为 甲 , 乙 ,则(
)
装号 证 考 准
只
2019年普通高等学校招生全国统一考试 高考模拟调研卷理科数学(二)(无答案)

普通高等学校招生全国统一考试 高考模拟调研卷理科数学(二)理科数学测试卷共4页。
满分150分。
考试时间120分钟。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的.(1) 集合{1012}M =-, , , ,集合{0246}N =, , , ,则=N M I(A ){11}-,(B ){1012}-, , , (C ){0246}, , , (D ){02},(2) 设1i +是方程20()x ax b a b R ++=∈,的一个根,则 (A )11a b ==,(B )22a b ==-,(C )22a b =-=, (D )21a b =-=-,(3) 已知A B , 两组数据如茎叶图所示,它们的平均数相同且2x y =,若将A B , 两组数据合在一起,得到的这组新数据的中位数是 (A )23 (B )24 (C )23.5 (D )24.5(4) 设x 、y 满足约束条件2022030x y x y x -+⎧⎪+-⎨⎪-⎩≥≥≤,则2z x y =-的最大值为(A )1(B )2(C )10(D )12(5) 若向量a b r r , 满足(2)a b a +⊥r r r ,()a b b +⊥r r r ,则a r 与b r的夹角为(A )45︒(B )60︒(C )120︒(D )135︒(6) 在ΔABC中,sincos 225C C =,10AB =,AC =BC = (A )5(B )8 (C )11 (D )5或11(7)命题:0p x ∀>;命题2:e 5x x q x R ∃∈=, (e 为自然对数的底数),则下列命题为真命题的是 (A )p q ∧(B )p q ⌝∨(C )p q ⌝∧ (D )p q ∨A 组B 组x1 4 6 42y9(8) 给图中的A B C D , , , 四块区域涂色,且相邻(有公共边的)区域不同色,现有四种不同颜色可供选用,则所有不同的涂色方法种数是 (A )36 (B )54 (C )84 (D )120(9) 执行如图所示的程序框图,若输入28=A ,6=B ,则输出的结果是 (A )2 (B )4 (C )6(D )28(10)已知椭圆22221(0)x y a b a b +=>>的右顶点、上顶点、右焦点分别为A B F , , ,22(1)BF BA a b ⋅=+-u u u r u u u r,则该椭圆的离心率为(A )2 (B )2 (C )12(D )4(11)已知0ab >,22a b ab +=,则21a b a b+++的最小值为 (A )34 (B )1 (C )54(D )32(12)已知()3sin 2cos f x x x x =++,当1a b +=时,不等式()(0)()(1)f a f f b f +>+恒成立,则实数a 的取值范围是 (A )(0)-∞,(B )1(0)2,(C )1(1)2,(D )(1)+∞,第Ⅱ卷本卷包括必考题和选考题两部分。
2019年普通高等学校招生全国统一考试高考模拟调研卷文科数学(二)数文答案2

高考模拟调研卷文科数学(二)参考答案 第1页 共3页2019年普通高等学校招生全国统一考试高考模拟调研卷文科数学(二)参考答案一、选择题 1~6 DCBCCD 7~12 ADDABB(12)解析:224422122323a b a b ab ab a b a b ab ab ab+++===+++++++,又22ab a b =+≥2ab ∴≥,故121a b a b+++≥,当且仅当22a b ==时,等号成立,故选B. 二、填空题(13)2 (14)0 (15)2 (16)100101(16)解析:2211111()(1)n n n n n n n n n n n n n S S S S S S S S S S S S S -----=--=--+⇒=-,即1111n n S S --=,1nn S ∴=,111(1)1n b n n n n ∴==-++,故前100项和为11001101101-=. 三、解答题(17)(本小题满分12分)解:(Ⅰ)616217S a a =⇒+=,又134a a +=,故1d =,11a =,n a n ∴=;……4分(Ⅱ)(5)n T n n =+,当2n ≥时124n n n b T T n -=-=+,当1n =时116b T ==,故对任意*n N ∈,24n b n =+,11111()2(2)42n n a b n n n n ==-++, 11113(1)42128n A n n ∴=+--<++.……12分 (18)(本小题满分12分)解:(Ⅰ)27947842ˆ 1.7708764b-⨯⨯==-⨯,ˆ42 1.7828.4a=-⨯=,故ˆ 1.728.4y x =+;…6分 (Ⅱ)由0.930.75>知,选择回归方程2ˆ0.17520y x x =-++拟合更好,代入9x =,可算得ˆ51.23y =,即总投入为9万元时的总产出约为51.23万. ……12分(19)(本小题满分12分)解:(Ⅰ)连接BD 交AC 于点O ,连接EO ,E O ,分别为DP DB , 的中点, 故//EO PB ,又EO ⊂平面EAC ,PB 不在平面EAC 内, 故//PB 平面EAC ;……6分 (Ⅱ)1124E ADCP ADC P ABCD V V V ---==,取AB 中点F ,连接PF ,则PF AB ⊥又面PAB ⊥面ABCD ,PF ∴⊥面ABCD122232P ABCD V -∴=⨯⨯=,12E ACD V -∴=. ……12分(20)(本小题满分12分)高考模拟调研卷文科数学(二)参考答案 第解:(Ⅰ)由题知圆心O '的横坐标为4p ,故3422p p +=,2p ∴=,抛物线C 的方程为24y x =; ……4分(Ⅱ)设1()2O m ', ,点200()4y P y , ,则22220011()()424y m y m -+-=+,即42004320y y --=, ∴208y =或4-(舍),0y ∴=,抛物线C 在点P 处的切线方程为2002()4y y y x =+, 即20x +=,若点O '在该切线上,则4m =,故存在满足条件的圆22127:()(28O x y '-+=. ……12分 (21)(本小题满分12分)解:(Ⅰ)()21x f x e x '=-+,故1()2f '=11()24f =,则切线方程为11))42y x -=-,即14y =; ……4分 (Ⅱ)由题知()210x f x ae x '=-+=有两个不等实根12x x , ,()2x f x ae ''=-,当0a ≤时,()0f x ''<,()f x '单调递减,不可能与x 轴有两个交点,故0a >,此时()f x '在2(ln )a -∞, 上单减,在2(ln )a+∞, 上单增,当x →-∞时,()0f x '>,当x →+∞时,()0f x '>,故只需2(ln )0f a'<,即322a e -<,22210x ae x -+=,∴22222222()31x f x ae x x x x =-+=--2235()24x =--+,223ln 2x a >>,故25()4f x <. ……12分(22)(本小题满分10分)解:(Ⅰ)曲线C 的普通方程为24y x =,直线l 的极坐标方程可化为:sin()sin (sin cos cos sin )sin sin cos sin x y ραθαραθαθαααα-=⇒-=⇒-=即cos (1)sin y x αα=-; ……5分(Ⅱ)显然(10)M , ,直线l 的参数方程为1cos sin x t y t αα=+⎧⎨=⎩(t 为参数),代入曲线C 的方程可得22sin 4cos 40t t αα--=, 故2416||||[16]sin 3MA MB α⋅=∈, . ……10分 (23)(本小题满分10分)解:(Ⅰ)即()f x 的最大值|42|m -≤,又()|3||7||37|10f x x x x x =+--+-+=≤,故|42|10m -≥,即3m ≥或2m -≤; ……5分 (Ⅱ)函数()y f x =的图象如右图所示,y kx=是过原点的直线,结合图形可知:当107k<<时,有三个交点,即方程有3个根;当107k=时,有两个交点,即方程有2个根;当107k>时,有一个交点,即方程有1个根. ……10分高考模拟调研卷文科数学(二)参考答案第3页共3页。
专题02 函数的概念与基本初等函数Ⅰ-2019年高考真题和模拟题分项汇编数学(文)(解析版)

=
4
+ 2π π2
1,
f
(π)
=
π −1+
π2
0 ,可知应为 D 选项中的图象.
2
7.【2019 年高考北京文数】在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗
星的星等与亮度满足
m2
–
m1
=
5 2
lg
E1 E2
,其中星等为 mk
的星的亮度为
Ek (k=1,2).已
知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为
=
−
1 2
,1
x
2
,其中 k>0.若在区间(0,9]上,关于 x 的方程 f (x) = g(x) 有
8 个不同的实数根,则 k 的取值范围是 ▲ .
【答案】
1 3
,
2 4
【解析】作出函数 f (x) , g(x) 的图象,如图:
由图可知,函数 f (x) = 1− (x −1)2 的图象与 g(x) = − 1 (1 x 2,3 x 4,5 x 6, 7 x 8) 的图象仅有 2 个交点,即在区间
专题 02 函数的概念与基本初等函数 I
1.【2019 年高考全国Ⅰ卷文数】已知 a = log2 0.2,b = 20.2, c = 0.20.3 ,则( )
A. a b c
B. a c b
C. c a b
D. b c a
【答案】B
【解析】 a = log2 0.2 log2 1 = 0, b = 20.2 20 = 1, 0 c = 0.20.3 0.20 = 1, 即 0 c 1, 则 a c b .故选 B.
河南省六市2019年高三第二次联合调研检测数学(理)试卷(有答案)

2019年河南省六市高三第二次联合调研检测数学(理科)试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试时间为120分钟,其中第Ⅱ卷22题,23题为选考题,其它题为必考题.考试结束后,将答题卡交回.注意事项:1.答题前,考生必须将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内.2.选择题必须用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.4.保持卡面清洁,不要折叠、不要弄破、不准使用涂改液、刮纸刀.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.已知集合A ={(x ,y )|y =x +1,x ∈Z },集合B ={y |y =2x ,x ∈Z },则集合A ∩B 等于A .{1,2}B .(1,2)C .{(1,2)}D .2.若复数z 满足(3-4i )z =|3-4i |,则z 的虚部为A .-4B .45C .4D .-453.某学校为落实学生掌握社会主义核心价值观的情况,用系统抽样的方法从全校2400名学 生中抽取30人进行调查.现将2400名学生随机地从1-2400编号,按编号顺序平均分 成30组(1-80号,81-160号,…,2321-2400号),若第3组与第4组抽出的号码 之和为432,则第6组抽到的号码是A .416B .432C .448D .4644.若等差数列{n a }的公差为2,且5a 是2a 与6a 的等比中项,则该数列的前n 项和n S 取最 小值时n 的值等于A .7B .6C .5D .45.设P 是正方体ABCD -A 1B 1C 1D 1的对角面BDD 1B 1(含边界)内的点,若点P 到平面ABC 、平面ABA 1、平面ADA 1的距离相等,则符合条件的点PA .仅有一个B .有有限多个C .有无限多个D .不存在6.已知Rt △ABC ,点D 为斜边BC 的的中点,|AB |=AC |=6,AE =12ED ,则AE ·EB 等于A .-14B .-9C .9D .147.设变量x ,y 满足不等式组001x y x y x ⎧⎪⎨⎪⎩+-4≤-3+3≤,≥则z =|x -y -4|的最大值为A .53B .72C .133D .6 8.函数22xx x f x -2-3()=的大致图象为9.设实数a ,b ,c 分别满足a =125-,b1nb =1,3c 3+c =1,则a ,b ,c 的大小关系为A .c >b >aB .b >c >aC .b >a >cD .a >b >c10.在直角坐标系xOy 中,F 是椭圆C :22221x y a b+=(a >b >0)的左焦点,A 、B 分别为左、右顶点,过点F 作x 轴的垂线交椭圆C 于P 、Q 两点,连接PB 交y 轴于点E ,连接AE 交PQ 于点M ,若M 是线段PF 的中点,则椭圆C 的离心率为A.2 B .12 C .13 D .1411.已知数列{n a }中,1a =1,且对任意的m ,n ∈N *,都有m n a +=m a +n a +mn ,则201911i i a ∑= =A .20192020B .20182019C .20181010D .2019101012.已知函数f (x )=sin2x 的图象与直线2kx -2y -k π=0(k >0)恰有三个公共点,这三个点的横坐标从小到大依次为x 1,x 2,x 3,则(x 1-x 2)tan (x 2-2x 3)=A .-2B .-12C .0D .1 第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分.13.已知tan (x +4)=2,x 是第三象限角,则cosx =_________.14.《易经》是中国传统文化中的精髓,右图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每卦有三根线组成(“”表示一根阳线,“”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率)_________.15.抛物线y 2=4x 的焦点为F ,其准线为直线l ,过点M (5,l 的垂线,垂足为H ,则∠FMH 的角平分线所在的直线斜率是__________.16.我国古代数学名著《九章算术》中有如下问题:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺。
【高考模拟】2019届高三入学调研考试卷 理科数学(二)(word版有答案)

2019届高三入学调研考试卷理 科 数 学(二)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2|230A x x x =--≥,{}2|4B x x =≤,则A B =( )A .[]2,1--B .[)1,2-C .[]1,1-D .[)1,2【答案】A【解析】由一元二次不等式的解法可得,集合{}{}223031A x x x x x x =--≥=≥≤-或,{}{}2|4|22B x x x x =≤=-≤≤, 所以{}[]212,1A B x x =-≤≤-=--,故选A . 2.i 为虚数单位,复数2ii 1z =-在复平面内对应的点所在象限为( ) A .第二象限 B .第一象限 C .第四象限 D .第三象限【答案】C【解析】()()2i 12i i 11i i 1i 1z --===--=---,复数2i i 1z =-在复平面内对应坐标为()1,1-,所以复数2ii 1z =-在复平面内对应的点在第四象限,故选C . 3.甲乙两名同学6次考试的成绩统计如下图,甲乙两组数据的平均数分别为甲x 、乙x ,标准差分别为,甲乙σσ,则( )A .甲乙x x <,甲乙σσ<B .甲乙x x <,甲乙σσ>C .甲乙x x >,甲乙σσ<D .甲乙x x >,甲乙σσ>【答案】C【解析】由图可知,甲同学除第二次考试成绩略低与乙同学,其他次考试都远高于乙同学,可知甲乙x x >,图中数据显示甲同学的成绩比乙同学稳定,故甲乙σσ<. 故选C .4.已知函数()324x f x x =+,则()f x 的大致图象为( )A .B .C .D .【答案】A【解析】因为()()324x f x f x x --==-+,所以函数为奇函数,排除B 选项,求导:()()42221204x x f x x'+=≥+,所以函数单调递增,故排除C 选项,令10x =,则()1000104104f =>,故排除D .故选A .5.已知向量)=a ,()0,1=-b ,(k =c ,若()2-⊥a b c ,则k 等于( )A .B .2C .3-D .1【答案】C【解析】因为()2-⊥a b c ,)2-=a b 0+,3k =-,故选C .6.已知函数()()2sin f x x ωϕ=+,()0,0ωϕ><<π的部分图像如图所示,则ω,ϕ的值分别是( )A .31,4πB .2,4πC .34ππ,D .24ππ,【答案】C 【解析】因为51244T =-,2T ∴=,2Tωπ∴==π,又因为324f ⎛⎫=- ⎪⎝⎭, 所以32sin 24ϕ⎛⎫π+=- ⎪⎝⎭,3sin 14ϕ⎛⎫∴π+=- ⎪⎝⎭,()3242k k ϕπ∴π+=-+π∈Z ,()524k k ϕπ∴=-+π∈Z ,0ϕ<<π,34ϕπ∴=,故选C . 7.若过点()2,0有两条直线与圆222210x y x y m +-+++=相切,则实数m 的取值范围是( ) A .(),1-∞- B .()1,-∞+ C .()1,0- D .()1,1-【答案】D【解析】由已知圆的方程满足2240D E F +->,则()44410m +-+>解得1m <; 过点有两条直线与圆相切,则点在圆外,代入有4410m -++>,解得1m >-, 综上实数m 的取值范围11m -<<,故选D .8.运行如图所示的程序框图,若输出的S 的值为21-,则判断框中可以填( )A .64?a <B .64?a ≤C .128?a <D .128?a ≤【答案】A【解析】运行程序如下:1a =,0S =,1S =,2a =-,12S =-,4a =,124S =-+,8a =-,1248S =-+-,16a =,124816S =-+-+,32a =-,1248163221S =-+-+-=-,64a =,故答案为A .9.抛物线()2:20E y px p =>的焦点为F ,点()0,2A ,若线段AF 的中点B 在抛物线上,则BF =( )A .54B .52C D 【答案】D【解析】点F 的坐标为,02p ⎛⎫⎪⎝⎭,所以A 、F 中点B 的坐标为,14p ⎛⎫ ⎪⎝⎭,因为B 在抛物线上,所以将B的坐标代入抛物线方程可得:212p =,解得:p =,则点F 坐标为⎫⎪⎪⎝⎭,点B 的坐标为⎫⎪⎪⎝⎭,由两点间距离公式可得BF =.故选D . 10.将半径为3,圆心角为23π的扇形围成一个圆锥,则该圆锥的内切球的体积为( )A B C .43π D .2π【答案】A【解析】设圆锥的底面半径为r ,高为h ,则2233r ππ=⨯,1r ∴=,h ==设内切球的半径为R 13=,R ∴=,334433V R =π=π=⎝⎭,故选A .11.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,且sin 1sin sin A bB C a c+=++,则C 为( )A .6π B .3π C .23π D .56π 【答案】B【解析】∵由正弦定理可得:sin 2a A R =,sin 2b B R =,sin 2c C R=, ∴sin 1sin sin A b a bB C a c b c a c+=+=++++,整理可得:222a b c ab +-=,∴由余弦定理可得:2221cos 22a b c C ab +-==,∴由()0,C ∈π,可得:3C π=.故选B .12.已知可导函数()f x 的定义域为(),0-∞,其导函数()f x '满足()()20xf x f x -'>,则不等式()()()22017201710f x x f +-+-<的解集为( ) A .(),2018-∞- B .()2018,2017-- C .()2018,0-D .()2017,0-【答案】B 【解析】令()()2,0f x g x x x =<,()()()()()243220x f x xf x xf x f x g x x x '--∴'==<',因为()()()22017201710f x x f +-+-<,所以()()()()2220172017201710x g x x g +--<++, 因为()g x 在(),0-∞单调递减,所以()()2017020170201820172017120171x x x g x g x +<+⎧⎪⎨⎪<⎧⇒⇒-<<-⎩⎨+<-+>-⎩,故选B .二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上)13.已知实数x ,y 满足约束条件2060 230x y x y x y -≥⎧⎪⎨+-≤-≤⎪⎩-,则23z x y =-的最小值是_____.【答案】8-【解析】实数x ,y 满足约束条件2060 230x y x y x y -≥⎧⎪⎨+-≤-≤⎪⎩-的可行域如图:目标函数23z x y =-,点()2,4A ,z 在点A 处有最小值:22348z =⨯-⨯=-, 故答案为8-.14.春节期间,某销售公司每天销售某种取暖商品的销售额y (单位:万元)与当天的平均气温x (单位:℃)有关.现收集了春节期间这个销售公司4天的x 与y 的数据列于下表:根据以上数据,求得y 与x 之间的线性回归方程y b x a =+的系数125b =-, 则a =________. 【答案】775【解析】由题意可得:235644x ----==-,20232730254y +++==,∴()12772ˆ5455a y bx -=+⨯-==.故答案为775. 15.已知某三棱柱的三视图如图所示,那么该三棱柱最大侧面的面积为__________.【解析】正视图、侧视图为长方形,俯视图为三角形的几何体为三棱柱,由图形可知面DA '的面积最16.在直角坐标系xOy 中,如果相异两点(),A a b ,(),B a b --都在函数()y f x =的图象上,那么称A ,B 为函数()f x 的一对关于原点成中心对称的点(A ,B 与B ,A 为同一对)函数()6sin 0 2log 0x x f x x x π⎧≤⎪=⎨⎪>⎩的图象上有____________对关于原点成中心对称的点.【答案】3【解析】()y f x =关于原点的对称图像的解析式为()y f x =--,因此()f x 关于原点对称的点的个数实际上就是()()f x f x =--在()0,+∞上解的个数.又当0x >时,()sin 2f x x π--=,考虑sin 2y x π=与6log y x =在()0,+∞上的图像的交点的个数.如下图所示,它们有3个公共点,从而()f x 有3对关于原点对称的点.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(12分)已知数列{}n a 的前n 项和n S 满足()2*2n n nS n +=∈N . (1)求数列{}n a 的通项公式;(2)设()*3n a n n b a n =⋅∈N ,求数列{}n b 的前n 项和n T . 【答案】(1)n a n =;(2)1313424n n n T +⎛⎫=+-⋅ ⎪⎝⎭. 【解析】(1)当2n ≥时,1n n n a S S n -=-=;当1n =时,111a S ==,符合上式. 综上,n a n =.(2)3n n b n =⋅,则1231323333n n T n =⋅+⋅+⋅+⋅⋅⋅+⋅, 234131323333n n T n +=⋅+⋅+⋅+⋅⋅⋅+⋅,∴()2311313233333313n nn n n T n n ++--=+++⋅⋅⋅+-⋅=-⋅-,∴1313424n n n T +⎛⎫=+-⋅ ⎪⎝⎭. 18.(12分)某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数y 与仰卧起坐个数x 之间的关系如下:0,03060,304080,4050100,50x x y x x ≤<⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:(1)计算a 值;(2)以此样本的频率作为概率,求①在本次达标测试中,“喵儿”得分等于80的概率; ②“喵儿”在本次达标测试中可能得分的分布列及数学期望. 【答案】(1)0.03a =;(2)见解析.【解析】(1)()0.010.010.05101a +++⨯=,∴0.03a =. (2)由直方图可知,“喵儿”的得分ξ情况如下:①在本次的三组测试中,“喵儿”得80分为事件A ,则“喵儿”可能第一组得80分, 或者第二组得80分,或者第三组得80分, 则()0.50.10.50.10.10.50.555P A =+⨯+⨯⨯=; ②()00.10.10.10.001P δ==⨯⨯=,()600.30.10.30.10.10.30.333P δ==+⨯+⨯⨯=, ()10010.0010.3330.5550.111P δ==---=,分布列如下:Eξ=⨯+⨯+⨯+⨯=.数学期望()00.001600.333800.5551000.11175.4819.(12分)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.(1)求证:AB1⊥平面A1BD;(2)求锐二面角A-A1D-B的余弦值;【答案】(1)见解析;(2【解析】(1)取BC中点O,连结AO.∵△ABC为正三角形,∴AO⊥BC.∵在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,∴AO⊥平面BCC1B1.OO,OA的方向为x,y,z轴的正方向建立空间直角坐标系:取B1C1中点O1,以O为原点,OB,1-,如图所示,则B(1,0,0),D(1,1,0),O xyzA1(0,2,A(0,0,B1(1,2,0),∴(11,2,AB=,()BD=-,(1BA=-.2,1,0∴10AB BD ⋅=,110AB BA ⋅=,∴1AB BD ⊥,11AB BA ⊥,∴AB 1⊥平面A 1BD .(2)设平面A 1AD 的法向量为(),,x y z =n .1,1,(AD =-,1,2,0(0)AA =.∵AD ⊥n ,1AA ⊥n ,∴100AD AA ⋅=⋅⎧⎪⎪⎩=⎨n n,∴020x y y ⎧-+-==⎪⎨⎪⎩,0y x ==⎧⎪⎨⎪⎩, 令1z =得(3,,1)0-=n 为平面A 1AD 的一个法向量.由(1)知AB 1⊥平面A 1BD ,1AB 为平面A 1BD 的法向量,∴1113cos AB AB AB ⋅--===-⋅n n,n . ∴锐二面角A -A 1D -B 的大小的余弦值为20.(12分)已知()23f x x =--,()21n g x x x ax =-且函数()f x 与()g x 在1x =处的切线平行.(1)求函数()g x 在()()1,1g 处的切线方程;(2)当()0,x ∈+∞时,()()0g x f x -≥恒成立,求实数a 的取值范围.【答案】(1)220x y ++=;(2)(],4-∞.【解析】(1)()2f x x '=-,()21n 2g x x a =+'-因为函数()f x 与()g x 在1x =处的切线平行所以()()11f g '='解得4a =,所以()14g =-,()12g '=-,所以函数()g x 在()()1,1g 处的切线方程为220x y ++=.(2)解当()0,x ∈+∞时,由()()0g x f x -≥恒成立得()0,x ∈+∞时, 221n 30x ax x -++≥即321n a x x x≤++恒成立, 设()321n (0)h x x x x x=++>,则()()()2223123x x x x h x x x +='-+-=, 当()0,1x ∈时,()0h x '<,()h x 单调递减,当()1,x ∈+∞时,()0h x '>,()h x 单调递增,所以()()min 14h x h ==,所以a 的取值范围为(],4-∞.21.(12分)设椭圆22221(0)x y a b a b+=>>的右顶点为A ,上顶点为B,AB =(1)求椭圆的方程;(2)设直线:(0)l y kx k =<与椭圆交于P ,Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM △的面积是BPQ △面积的2倍,求k 的值.【答案】(1)22194x y +=;(2)12-. 【解析】(1)设椭圆的焦距为2c ,由已知得2259c a=,又由222a b c =+,可得23a b =.由AB =3a =,2b =. 所以椭圆的方程为22194x y +=. (2)设点P 的坐标为()11,x y ,点M 的坐标为()22,x y ,由题意,210x x >>,点Q 的坐标为()11,x y --.由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ ,从而()21112x x x x -=--⎡⎤⎣⎦,即215x x =.易知直线AB 的方程为236x y +=,由方程组236x y y kx +==⎧⎨⎩,消去y ,可得2632x k =+. 由方程组22194x y y kx ⎧+==⎪⎨⎪⎩,消去y,可得1x = 由215x x =()532k =+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-. 当89k =-时,290x =-<,不合题意,舍去; 当12k =-时,212x =,1125x =,符合题意. 所以,k 的值为12-. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(10分)【选修4-4:坐标系与参数方程】以平面直角坐标系的原点为极点,x 轴的正半轴为极轴,建立极坐标系,已知直线l的参数方程是()0,12x m m t y t ⎧⎪⎪⎨=+⎩>=⎪⎪为参数,曲线C 的极坐标方程为2cos ρθ=. (1)求直线l 的普通方程和曲线C 的直角坐标方程;(2)若直线l 与x 轴交于点P ,与曲线C 交于点A ,B ,且1PA PB ⋅=,求实数m 的值.【答案】(1)见解析;(2)1m =1.【解析】(1)直线l的参数方程是()0,12x m m t y t ⎧⎪⎪⎨=+⎩>=⎪⎪为参数, 消去参数t可得x m =+.由2cos ρθ=,得22cos ρρθ=,可得C 的直角坐标方程:222x y x +=.(2)把()12x m t y t ⎧⎪⎪⎨⎪⎪⎩=+=为参数,代入222x y x +=,得2220t t m m +-+-=. 由0∆>,解得13m -<<,∴2122t t m m =-, ∵121PA PB t t ⋅==,∴221m m -=±,解得1m =或1.又满足0∆>,0m >,∴实数1m =1.23.(10分)【选修4-5:不等式选讲】 设函数()212f x x x =--+.(1)解不等式()0f x >;(2)若0x ∃∈R ,使得()2024f x m m +<,求实数m 的取值范围.【答案】(1)1|33x x x ⎧⎫⎨<>⎩⎭-⎬或;(2)1522m -<<. 【解析】(1)函数()3,21212=31,2213,2x x f x x x x x x x ⎧⎪-+<-⎪⎪=--+---≤≤⎨⎪⎪->⎪⎩, 令()0f x =,求得13x =-,或3x =, 故不等式()0f x >的解集为1|33x x x ⎧⎫⎨<>⎩⎭-⎬或; (2)若存在0x ∃∈R ,使得()2024f x m m +<,即()2042f x m m <-有解,由(1)可得()f x 的最小值为11531222f ⎛⎫=-⨯-=- ⎪⎝⎭, 故25422m m -<-,解得1522m -<<.。
2019年普通高等学校统一招生考试调研卷(二)数学

半部分,则剩余几何体的侧视图为( )
高考调研卷
数学调研卷(二)·第 1 页(共 12 页)
2019·群模考
小梦学习园地系列试卷
A
B
C
4.若 sin
3 5
,
是第三象限角,则
sin
4
(
)
A. 2
10
B. 7 2
10
C. 2
10
5.
a x
3
x2
7
的展开式中,
E
于
M
,
N
两点, O
为坐标原点,问: OM
ON
是否
为定值?若是,请求出定值;若不是,请说明理由.
高考调研卷
数学调研卷(二)·第 5 页(共 12 页)
2019·群模考
小梦学习园地系列试卷
6
21.(本小题满分 12 分)已知函数 f x 1 ax2 1 2a x 2ln x , a R ;
高考调研卷
数学调研卷(二)·第 6 页(共 12 页)
2019·群模考
小梦学习园地系列试卷
7
文科卷【文科生做答】
第Ⅰ卷 (选择题 共 60 分)
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符合题 目要求的.
1.已知集合 A x 1 x 2 , B x x x 3 0 ,则集合 A B ( )
A.
B.
C.
D.
10.已知空间四边形
ABCD
,
BAC
2 3
,
AB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
年高考数学专题02高考考前调研卷二-2019最新整理
【试题说明】命题者认真研究近几年新课标全国卷高考试题,命题时严格按照全国Ⅰ卷格式编排,以最新发布的2018年全国卷《考试说明》为依据,内容确保不超纲。
调研卷体现高考“前瞻性”和“预测性”。
试卷力争做到形、神与新课标全国卷风格一致,让学生和教师有“高考卷”的感觉。
试卷中知识点分布、试卷的总字数(包括各科选择题的题干字数、大题材料的长度、信息的有效性)、选项文字的长度、答案的规范、难易度的梯度等,都要符合高考试卷特点。
一.选择题
1.已知集合A=,则 ( ).2{|230},{|ln(1)}x x x B x y x --≤==-A B =
A.(1,3)
B.
C.
D.(-1,2)(1,3][1,2)-
【答案】.B
【解析】,2{|230}{|13}[1,3]A x x x x x =--≤=-≤≤=-
{|ln(1)}{|10}(1,)B x y x x x ==-=->=+∞,所以A B =(1,3]
2. 若复数是虚数单位)的实部和虚部相等,则等于( )(,i 12a i z a R i
+=
∈-|4|a i + A .2 B .3 C .4 D .8
【答案.】C
3.双曲线的一条渐近线和圆相交截的弦长是1,则双曲线的方程是( )
2
221(0)x y a a
-=>22(2)2x y +-= A. B. 2213x y -=2
212
x y -= C. D.2221x y -=2231x y -=
【答案】.D
【解析】双曲线的一条渐近线设为,利用渐近线与圆相交截得的弦长是2,所以
圆心到直线的距离d=,即2
221(0)x y a a
-=>x y a =22(2)2x y +-=1=
1=,解得,所以双曲线的方程是。
213
a =2231x y -= 4.下面的几何体是圆锥的一半和一个三棱锥组成,正视图和侧视图如图所示,则俯视图可能是( )
A. B.C. D.
【答案】.A 【解析】根据题意该几何体是圆锥的一半和一个三棱锥组成,只有A 满足题意。
5.《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织的快,而且每天增加的数量相同,已知第一天织布5尺,一个月(按30天计算)总共织布390尺,问第五天织布的数量为多少尺?该问题的答案为( )
A .尺
B .尺
C .尺
D .尺
92920129209292029 【答案】.C。
