柯西极限存在准则
函数极限的柯西收敛准则

写完之后我想看看其他人是怎么证明的搜索了一下拉格朗日中值定理的辅助函数的构造结果发现自己写的这篇博客居然排名第一
函数极限的柯西收敛准则
以下内容来自中科大数学分析教程P73,定理2.4.7 函数在x_{0}点的极限的定义 若存在l,\forall \epsilon>0,\exists\delta>0,使得当|x-x_{0}|<\delta 则有|f(x)-l|<\epsilon,即称l为f(x)当x趋近于x_{0}的极限 定理:函数f(x)在x_{0}处有极限的充要条件是\forall \epsilon>0,\exists\delta>0, \quad\quad 使得任意x_{1},x_{2}\in U(x_{0},\delta)时,有 \quad\quad |f(x_{1})-f(x_{2})|<\epsilon 证明: 1.必要性 若f(x)在x_{0}点的极限为l,即\forall \frac{\epsilon}{2}>0,\exists\delta,当x_{1},x_{2}\in U(x_{0},\delta) 有|f(x_{1})-l|<\frac{\epsilon}{2},|f(x_{2})-l|<\frac{\epsilon}{2} 则:|f(x_{1})-f(x_{2})|=|f(x_{1})+l-l-f(x_{2})| \quad\quad \leqslant |f(x_{1})-l|+|f(x_{2})-l| \ห้องสมุดไป่ตู้uad\quad\leqslant\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon
柯西收敛准则

柯西收敛准则
收敛准则(又称柯西极限存在准则),是用来判断某个式子是否收敛的充要条件(不
限于数列),主要应用在以下方面:数列、数项级数、函数、反常积分、函数列和函数项
级数每个方面都对应一个柯西准则,因此下文将按照不同的方面对准则进行说明。
反常积分:反常积分分为两种,一种是积分区间含有无穷大的反常积分(又叫做无穷
限的反常积分),另一种是被积函数为无界函数的反常积分(又叫做无界函数的反常积分、瑕积分)。
因此相应的柯西收敛准则有两种,两种准则的描述有些区别,但都可以根据函
数的柯西收敛准则来证明。
函数:考虑到数列就是特定的函数(即为定义域为正整数集),可以悖论,函数的敛
散性也应存有相似的结论,这就是接下来要说的函数的柯西发散准则。
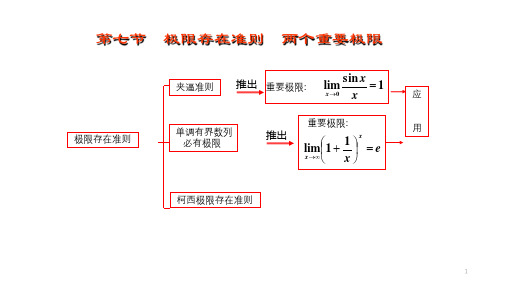
极限存在准则两个重要极限

一、 极限存在准则
定理20
(单调有界准则)单调有界数 列必有极限.
设数列{xn}单调增加,且 xn≤M.从图2-9可以看出,因为数 列单调增加又不能大于M,故该 数列某项以后的所有项必然集中 在某数a(a≤M)的附近,即对ε>0, 必然存在正整数N与数a,使当 n>N时,恒有xn-a<ε,从而数 列{xn}的极限存在.
N=max{N1,N2},则当n>N
yn-a<ε,zn-a<ε,
a-ε<yn<a+ε,a-ε<zn<a+ε, 从而,当n>N a-ε<yn≤xn≤zn<a+ε, 即xn-a<ε,所以limn→∞ xn=a.
一、 极限存在准则
注
利用定理18求极限,关键是构造出极限相同且易求 的两个数列yn与zn.
【例29】
二、 两个重要极限
数学中常常会对一些重要且有典型 意义的问题进行研究并加以总结,以期 通过对该问题的解决带动一类相关问题 的解决,下面介绍的重要极限就体现了 这样的一种思路,利用它们并通过函数 的恒等变形与极限的运算法则就可以使 得两类常用极限的计算问题得到解决.
二、 两个重要极限
1.
证在图2-10所示的单位圆中,设 ∠AOB=x,先假设0<x< ,点A处的 切线与OB的延长线相交于点D,又 BC⊥OA
谢谢聆听
【例35】
三、 柯西极限存在准则
定理21
(柯西极限存在准则)数列{xn}收敛的充分必要条件是:对于任意 给定的正数ε,存在正整数N,使得当m>N,n>N
xm-xn<ε. 证必要性.设limn→∞ xn=a,则对于ε>0,由数列极限的定义,v 正整数N,当n>N
第十讲 柯西收敛准则

第十讲、柯西收敛准则定理10.1 . (柯西收敛准则)数列{}n x 极限存在的充要条件是:对于0ε∀>存在正数 N , 使当n N >时, 对于一切p +∈ 有||n p n x x ε+−<注记10.1. (I )柯西准则的意义是:数列{}n x 是否有极限可以根据其一般项的特性得出,而不必事先知晓其极限的具体值(见下面的例子10.2)。
(II )定理10.1的逆否命题为:(柯西收敛准则)数列{}n x 极限不存在的充要条件是: 00ε∃>,使得对 +N ∀∈ , 均存在n N >时, 存在p +∈ ,使得0||n p n x x ε+−≥例子10.1设sin 2n n x n =,试用柯西收敛准则证明该数列极限存在。
证明:注意到sin 2()sin 2sin 2()sin 2||=112n p n n p n n p n x x n p n n p nn p n n +++−−≤+++≤+≤+于是,对0ε∀>,取正数 2=N ε, 则当n N >时, 对于一切p +∈ 有2||n p n x x n ε+−≤<。
故由定理10.1柯西收敛准则可知sin 2lim n n n →∞存在。
证毕。
例子10.2.设222111123n x n =++++ ,证明数列{}n x 收敛。
证明:注意到222111||=(1)(2)()111(1)(1)(2)(1)()1111111121111n p n x x n n n p n n n n n p n p n n n n n p n p n n p n+−++++++≤+++++++−+ =−+−++− ++++−+=−<+ 于是,对0ε∀>,取正数 1=N ε, 则当n N >时, 对于一切p +∈ 有1||n p n x x nε+−≤<。
故由定理10.1柯西收敛准则可知222111lim 123n n →∞ ++++ 存在。
函数极限的柯西收敛准则

函数极限的柯西收敛准则柯西收敛准则是指数列收敛的一种判据,它是由法国数学家柯西(Augustin Cauchy)在19世纪初提出的。
柯西收敛准则主要应用于函数极限的研究中,通过判断数列的柯西条件是否满足来确定数列是否收敛。
柯西收敛准则的数学表述如下:对于任意给定的正数ε,存在正整数 N,对任意的m,n≥ N,都有,an - am,< ε 成立。
直观来解释柯西收敛准则就是当数列中的一段数列的值无限接近时,整个数列也会收敛。
柯西收敛准则可以用来证明一个数列收敛,但是对于具体的极限值并没有给出明确的方法。
对于函数极限来说,柯西收敛准则可以用来证明一个函数在特定点处的极限存在。
具体来说,对于函数f(x),如果对任意给定的正数ε,存在正实数δ,使得对于所有的x1,x2∈(c-δ,c+δ),都有,f(x1)-f(x2),<ε成立,则f(x)在点c处的极限存在。
柯西收敛准则的证明通常通过数列的收敛性和函数的连续性来进行。
对于函数极限的柯西收敛准则,可以通过数列的柯西性和函数的其中一种性质(例如连续、有界等)来进行证明。
以函数极限的柯西收敛准则的证明为例,我们先假设函数f(x)在点c 处具有极限L,然后构造一个数列{x_n},使得{f(x_n)}满足柯西收敛准则。
首先,对于给定的正数ε,由于f(x)在点c处极限存在,存在正实数δ1,使得当,x-c,<δ1时,,f(x)-L,<ε/2成立。
然后,我们选取一个数列{x_n},使得对于任意的正整数n,,x_n-c,<δ1/n成立。
显然,当n较大时,x_n-c,较小,这意味着{x_n}收敛于c。
接下来,我们考虑数列{f(x_n)}。
由于f(x)在点c处连续,根据ε-δ定义,存在正整数N,使得对于任意的m,n≥N,都有,x_n-x_m,<δ1,从而有,f(x_n)-f(x_m),<ε/2成立。
综上所述,数列{f(x_n)}满足柯西收敛准则,从而根据柯西收敛定理,数列{f(x_n)}收敛于一些极限值,假设为L'。
高等数学 第1章 第七节 极限存在准则 两个重要极限
则
lim
n
x n1
lim n
6 xn ,
A
6 A,
解得 A 3或A 2,(舍去)
lim n
xn
3.
14
3.两个重要极限的应用
例6: 求 lim tan x 1
x0 x
可作为公式
lim
x
s
in u x ux
1
lim ux 0
x
解: lim tan x lim sin x 1 lim sin x lim 1 11 1 x0 x x0 x cos x x0 x x0 cos x
1 n2 1
n2
1
22
n2
1
n2
n n2 1
,
1
lim 1 0, n 2n
lim n n n2 1
lim n
n
1
1
由夹逼定理知:
n2
0 0, 10
lim n
n
1 2
1
n2
1 22
n2
1 n2
存在, 且
lim n
n
1 2
1
n2
1
22
n2
1
n2
0.
8
例2 用夹逼准则证明:
lim sin x 1.
1yn xn zn n 1,2,3,,
2
lim
n
yn
a,
lim
n
z
n
a,
则数列x
n
的
极
限
存
在,
且
lim
n
xn
a.
准则1 若
1当x
U
x
极限不存在的证明

不如何证明极限不存在一、归结原则原理:设f 在);('00δx U 内有定义,)(lim 0x f x x →存在的充要条件是:对任何含于);('00δx U 且以0x 为极限的数列{}n x 极限)(lim n n x f ∞→都存在且相等。
例如:证明极限xx 1sinlim 0→不存在 证:设),2,1(221,1⋯=+="='n n x n x n n πππ,则显然有 ,)(0,0∞→→"→'n x x n n )(111sin ,001sin ∞→→="→='n x x nn 由归结原则即得结论。
二、左右极限法原理:判断当0x x →时的极限,只要考察左、右极限,如果两者相等,则极限存在,否则极限不存在。
例如:证明)1arctan()(xx f =当0→x 时的极限不存在。
因为2)1arctan(lim 0π-=-→x x x=0,2)1arctan(lim 0π=+→x x ,)1arctan(lim )1arctan(lim 00xx x x +-→→≠,所以当0→x 时,)1arctan(x的极限不存在。
三、证明∞→x 时的极限不存在原理:判断当∞→x 时的极限,只要考察-∞→x 与+∞→x 时的极限,如果两者相等,则极限存在,否则极限不存在。
例如:证明x e x f =)(在∞→x 时的极限不存在因为0lim =-∞→x x e ,+∞=+∞→x x e lim ;因此,x x x x e e +∞→-∞→≠lim lim 所以当∞→x 时,x e 的极限不存在。
四、柯西准则原理:设f 在);('00δx U 内有定义,)(lim 0x f x x →存在的充要条件是:任给0>ε,存在正数)(δδ'<,使得对任何);(,00δx U x x ∈''',使得0)()(ε≥''-'x f x f 。
一致连续与柯西收敛准则

2. 一致连续性
设函数f ( x)在区间I上有定义,如果对于任意给定的 正数ε,总存在着正数δ,使得对于区间I上的任意两点x1、 x2,当 x1 − x2 < δ时,就有 f ( x1 ) − f ( x2 ) < ε , 那么称函数f ( x)在区间I上是一致连续的。
2 n
其中 0 < q < 1,
证明: 证明: n > m时,
ai ≤ M(常数) .
xn − xm = am +1q m +1 + am + 2 q m + 2 + L + an q n
1− qm M m m +1 ≤ Mq < q , 1− q 1− q
M m ∀ε > 0, 欲使 xn − xm < ε , 只要 q < ε, 1− q
1− q ln ε M , 或只要 m > ln q
1− q ln M ε , 则当n, m > N时,恒有 故取正整数N ≥ ln q
xn − xm < ε ,
所以,由柯西收敛准则知,数列{xn }收敛。
例2. 写出极限 lim f ( x)存在的柯西收敛准则及其否定描述。
∴ f ( x)在区间[a,+∞)上一致连续。
1 例10. 证明 : 若函数f ( x) = e cos 在区间(0,1)上非一致连续。 x
x
证明: 证明: 给定正数ε(< 1 , 对任意的正数δ,总有 ) 0
1 1 x1 = , x2 = ,∈ (0,1), π 2nπ 2nπ + 2 x1 − x2 < δ , (n充分大时总可成立)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
柯西极限存在准则
柯西极限存在准则又叫柯西收敛原理,给出了数列收敛的充分必要条件。
数列{Xn}收敛的充分必要条件是:对于任意给定的正数ε,存在着这样的正整数N,使得当m>N,n>N时就有|Xn-Xm|<ε这个准则的几何意义表示,数列{Xn}收敛的充分必要条件是:对于任意给定的正数ε,在数轴上一切具有足够大号码的点Xn中,任意两点间的距离小于ε .
充分性证明:
(1)、首先证明Cauchy列有界
取ε=1,根据Cauchy列定义,存在自然数N,对一切n>N,有
Ia(n)-a(N+1)I<1。
令M=max{|a(1)|,|a(2)|,…,|a(N)|,|a(N+1)|+1}
则对一切n,成立|a(n)|≤M。
所以Cauchy列有界。
(2)、其次在证明收敛
因为Cauchy列有界,所以根据Bolzano-Weierstrass定理(有界数列有收敛子列)存在一个子列aj(n)以
A为极限。
那么下面就是要证明这个极限A也就是是Cauchy列的极限。
(注意这种证明方法是实数中常用
的方法:先取点性质,然后根据实数稠密性,考虑点领域的性质,然后就可以证明整个实数域的性质了)
因为Cauchy列{a(n)}的定义,对于任意的ε>0,都存在N,使得m、n>N时有
|a(m)-a(n)|<ε/2
取子列{aj(n)}中一个j(k),其中k>N,使得
|aj(k)-A|<ε/2
因为j(k)>=k>N,所以凡是n>N时,我们有
|a(n)-A|<=|a(n)-aj(k)|+|aj(k)-A|<ε/2+ε/2=ε
这样就证明了Cauchy列收敛于A.
即得结果:Cauchy列收敛。
