第3章 热力学第二、三定律 第5节 第二定律的本质和熵的统计意义
熵与热力学第二定律

熵与热力学第二定律热力学是一门研究能量转化和传递的学科,而熵则是热力学的一个重要概念。
熵是描述系统无序度的物理量,也可以理解为系统的混乱程度。
热力学第二定律则给出了一个有关熵变化的基本规律,对于理解自然界中各种现象都具有重要意义。
首先,我们来了解一下熵的概念。
熵最初由德国物理学家鲁道夫·克劳修斯在19世纪提出,用以描述能量在转化和传递过程中的无序度。
熵的单位是焦耳/开尔文(J/K)。
在热力学中,我们通常用S表示熵。
对于一个封闭系统来说,其熵的变化可以通过以下公式表示:ΔS = Q/T其中,ΔS表示熵变化,ΔQ表示系统所吸收或释放的热量,T表示温度。
从这个公式可以看出,熵的变化与温度和能量的传递有着密切的关系。
进而,熵的变化与热力学第二定律密切相关。
热力学第二定律是热力学中的一条基本定律,它通过熵的变化来描述了自然界中一种普遍存在的变化趋势:任何一个孤立系统总是朝着熵增的方向进行变化。
热力学第二定律可以用以下两种表述方式进行阐述:1. 克劳修斯表述:不可能自发地将热量从低温物体传递到高温物体,而不做额外的功。
这个表述是从能量守恒的角度上来看待熵增的原理。
2. 开尔文表述:不可能从单一热源吸热,使之完全转化为有效功而不产生其他变化。
这个表述则是从热力学循环的角度上来看待熵增的原理。
无论是克劳修斯表述还是开尔文表述,都体现了一个重要的观点:自然界的变化总是朝着更高的熵方向发展,即朝着能量的分散和无序性的增加。
这进一步表明了熵在物理系统中的重要性。
熵的概念不仅在热力学领域有着广泛的应用,还可以引申到其他领域。
在信息论中,熵被用来度量信息的不确定性,即信息的无序度。
熵在信息论中与热力学中的熵有着数学上的相似性,都是描述系统无序度的物理量。
这种类比为信息论提供了一个重要的工具,使之能够研究信息的流动和传递。
总结起来,熵是热力学中一个重要的概念,用于描述系统的无序度。
熵的变化与热力学第二定律密切相关,从而给出了自然界中的一种普遍存在的变化趋势。
§7-9 熵增加原理 热力学第二定律的统计意义

m dV R M V
不可逆
o V1
V2 V
m V2 R ln 0 M V1
§7-9 熵增加原理 热力学第二定律的统计意义 设在微小时间 t 内, 从 A 传到 B 的热量为 Q. 例2 求热传导中的熵变
Q
Q S A TA
TA
TA TB
TB绝Leabharlann 壁Q Q S S A S B TA TB
§7-9 熵增加原理 热力学第二定律的统计意义 证明 理想气体真空膨胀过程是不可逆的 .
Q 0, A 0, E 0, T 0
p
1
2
( p1 ,V1 , T )
( p2 ,V2 , T )
在态1和态2之间假设一可逆 等温膨胀过程
S 2 S1
2 dQ 1
T
V2 V1
不可逆过程 非平衡态 平衡态(熵增加) 自发过程 熵增加原理成立的条件: 孤立系统或绝热过程.
§7-9 熵增加原理 热力学第二定律的统计意义
熵增加原理的应用 :给出自发过程进行方向
的判椐 . 五 熵增加原理与热力学第二定律
热力学第二定律亦可表述为 : 一切自发过程
总是向着熵增加的方向进行 .
§7-9 熵增加原理 热力学第二定律的统计意义
Q S B TB
TA TB
S 0
同样,此孤立系统中不可逆过程熵亦是增加的 .
§7-9 熵增加原理 热力学第二定律的统计意义
三 熵增加原理:孤立系统中的熵永不减少.
S 0
孤立系统不可逆过程
孤立系统可逆过程
S 0 S 0
孤立系统中的可逆过程,其熵不变;孤立系统 中的不可逆过程,其熵要增加 . 平衡态 A 可逆过程 平衡态 B (熵不变)
热力学第二定律的统计解释
3 – 9 热力学第二定律的统计意义
第三章热力学基础
N1
2
4
N
Ω
(左)
2
22
24
2N
0
N个分子,Ωi
2 N。
若N=100, 则:
Ωi 2100 1030
而左右各半的平衡态及其附近宏观态的热力学概率则
占总微观状态数的绝大比例。 Ω(N左)
一般热力学系统 N的数量级约
N 很大
为1023,上述比例实际上是百分
概率小的状态
概率大的状态
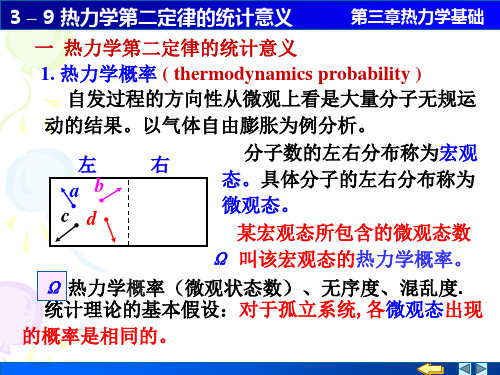
讨论 N 个粒子在空间的分布问题
可分辨的粒子集中在 左空间的概率
N 1, 2
N 2, 4
3 – 9 热力学第二定律的统计意义
第三章热力学基础
b Aa
B
cd
ab
bc
c
a dcd
a bd
a bd
c
1 1264
A
bBa
cd
bd c
a
ab
c d
分子的分布
容器 A
的部
分B
设 S f(),求 f 的函数形式。
由 S 的可加性来分析:
1 S1, 1
1+2
S,
2 S2, 2 1、2彼此独立
∴ 应有: f( ) ln
3 – 9 热力学第二定律的统计意义
第三章热力学基础
S k ln
─ 玻耳兹曼熵公式
1877年玻耳兹曼提出了S ln 。
1900年普朗克引进了比例系数 k 。
ab cd
0
0a
b
c
d
bc ac ab a a d d d bc b
abbc cd d
熵的应用和意义

浅谈熵的意义及其应用摘要:介绍了熵这个概念产生的原因,以及克劳修斯对熵变的定义式;介绍了玻尔兹曼从微观角度对熵的定义及玻尔兹曼研究工作的重要意义;熵在信息、生命和社会等领域的作用;从熵的角度理解人类文明和社会发展与环境的关系。
关键词:克劳修斯熵玻尔兹曼熵信息熵生命熵社会熵0 前言:熵是热力学中一个非常重要的物理量,其概念最早是由德国物理学家克劳修斯(R.Clausius)于1854年提出,用以定量阐明热力学第二定律,其表达式为dS=(δQ/T)rev。
但克劳修斯给出的定义既狭隘又抽象。
1877年,玻尔兹曼(L.Boltzmann)运用几率方法,论证了熵S与热力学状态的几率W之间的关系,并由普朗克于1900给出微观表达式S=k logW,其中k为玻尔兹曼常数。
玻尔兹曼对熵的描述开启了人们对熵赋予新的含义的大门,人们开始应用熵对诸多领域的概念予以定量化描述,促成了广义熵在当今自然及社会科学领域的广泛应用【1】【2】。
1 熵的定义及其意义克劳修斯所提出的熵变的定义式为dS=(δQ/T)rev,由其表达式可知,克劳修斯用过程量来定义状态函数熵,表达式积分得到的也只是初末状态的熵变,并没有熵的直接表达式,这给解释“什么是熵”带来了困难。
【1】直到玻尔兹曼从微观角度理解熵的物理意义,才用统计方法得到了熵的微观表达式:S=k logW。
这一公式对应微观态等概出现的平衡态体系。
若一个系统有W个微观状态数,且出现的概率相等,即每一个微观态出现的概率都是p=1/W,则玻尔兹曼的微观表达式还可写为:S=-k∑plogp。
玻尔兹曼工作的杰出之处不仅在于它引入了概率方法,为体系熵的绝对值计算提供了一种可行的方案,而且更在于他通过这种计算揭示了熵概念的一般性的创造意义和价值:上面所描述的并不是体系的一般性质量和能量的存在方式和状态,而是这些质量和能量的组构、匹配、分布的方式和状态。
玻尔兹曼的工作揭示了正是从熵概念的引入起始,科学的视野开始从对一般物的质量、能量的研究转入对一般物的结构和关系的研究,另外,玻尔兹曼的工作还为熵概念和熵理论的广义化发展提供了科学依据。
材料热力学3-1第二 第三定律

T2 S 3 nC p , m H 2 O, s ln T1
ΔS环境?????
恒压条件下:
S 环境
H m 263 . 15 H 1 H m 273 . 15 H 3 1 75 . 3 10 6020 37 . 6 10 5463 J H m 263 .15 K S 环境 21 .44 J K 1 263 .15 K
解:由于是正常相变:
QR S T
n fu s H m 1 5995 . 8 273 .15 T 1 1 22 . 01( J K m ol )
2. 不可逆相变:定温定压下两相不平衡时的相变。 不是发生在两相平衡共存的T,P下的相变——不可逆相变
亚(介)稳态:过冷、过热的液体;过 饱和溶液等。 不可逆相变的ΔS 计算:
不可逆过程: H2O (l)263K p0
需 计 逆 程 计 ΔS
设 可 过 来 算
ΔS=?
H2O (s)263K p0
等压可 逆降温
ΔS1
等压可 逆升温
ΔS3
H2O (l)273K p0
ΔS2
可逆相变
H2O (s) 273K p0
H2O (l)263K
p0
ΔS=?
H2O (s)263K p0
等压可 逆降温
pdV = nRT
∫
V1 +V 2 V1
dV V 1+V 2 = nRT ln V V1
Q V 1+V 2 S = S 2 _S 1 = = nR ln T V1
1mol理想气体在298K时等温膨胀,体积增大10倍,求系统的熵
物理化学热力学第二定律重点归纳

一、内容提要:热力学第二定律是在研究热功转化的效率的过程中发展和建立起来的。
热力学第二定律的主要任务,是解决过程的方向和限度问题,为了解决这个问题,本章首先从常见的自发过程入手,发现自发变化过程都有一定的方向和限度,而自发过程能否成为可逆过程的问题又可归结到热是否能够全部转换为功而不引起其他变化(结论是不能)的问题,从而得出自发过程的共同特征—不可逆性,根据自发变化的这一规律性引出了热力学第二定律的经验叙述。
然后通过研究热功转化的理想循环—卡诺循环、归纳出卡诺定理,解决了热功转换的最大效率问题;得出卡诺循环的热温商之和为零,然后将卡诺循环的这个特点推广到任意的可逆循环从而得到了热力学第二定律的基本状态函数—熵,再通过可逆循环和不可逆循环过程的热温商的推导,得出熵变的计算方法以及熵变与过程的热温商之和之间的关系,从而得出了热力学第二定律的数学表达式—克劳修斯不等式和熵增原理,将熵增原理应用于孤立系统因而得出了熵判据,根据熵判据,我们可以判断所有过程的方向和限度(或者平衡条件)。
(一) 自发过程的共同特征——不可逆性,且都可以归结到热功交换的不可逆性。
(二) 热力学第二定律表述:1、Clausius 说法:不可能把热从低温物体传到高温物体而不引起其他变化。
这一说法揭示了热量传递的不可逆性2、Kelvin 说法:不可能从单一热源取热,使之完全转变为功而不发生其它变化,这一说法揭示了热功交换的不可逆性。
Kelvin 的另一说法:第二类永动机是不可能制成的。
人们在研究热功转化规律的基础上,抓住了事物的共性,提出了具有普遍意义的熵函数,根据熵函数和由此导出的另两个状态函数—亥姆霍兹自由能和吉布斯自由能,可以较简便的解决化学反应的方向和限度问题。
这就是热力学第二定律的重要作用和目的。
(三)卡诺循环结论:h l h l 0Q Q T T += (由此结论得出了得到了热力学第二定律的基本状态函数-熵)(四)卡诺定律:IR R ηη<,热力学第二定律证明,工作于同温热源与同温冷源之间的所有热机,可逆热机的效率最大。
热力学第二定律与熵

热力学第二定律与熵热力学第二定律是热力学中的基本定律之一,与能量转化的方向和效率有关。
它描述了一个闭合系统中热量无法从低温物体自发地传递到高温物体的现象,并提出了一个重要的热力学量——熵。
一、热力学第二定律的基本原理热力学第二定律有多种表述方式,其中最常见的是开尔文表述和克劳修斯表述。
开尔文表述认为热量自发地只能从高温物体传递到低温物体,不可能反向传递。
这可以用热力学系统的能量转化过程来解释,即热量只能自发地由高温区域向低温区域传递,而不能自行实现相反的过程。
克劳修斯表述则强调系统熵的增加,即一个孤立系统的熵总是不断增加的。
熵可以理解为系统的无序程度或混乱程度。
克劳修斯表述意味着热力学过程总是趋向于增加系统的熵,即趋向于增加系统的混乱程度。
这也可以解释为什么一切自发发生的过程都是不可逆的。
二、热力学第二定律的两种熵增表达式热力学第二定律可以通过熵增来表达。
熵增等于热量的流入量除以温度的比值,即ΔS = Q/T,其中ΔS表示熵增,Q表示热量,T表示温度。
这个公式是一个定量描述系统熵的变化的表达式,通过计算系统的输入和输出热量以及热力学温度的比值,可以得到系统熵的变化情况。
另外,还有一个更常见的表达式,即ΔS = Qrev/T,其中ΔS表示熵增,Qrev表示可逆过程中系统所吸收的热量,T表示热力学温度。
这个表达式中的热量只考虑了可逆过程中的热量变化,反映了系统在可逆过程中熵的变化情况。
这两种熵增表达式都可以用于定量计算系统熵的变化。
三、熵与系统可逆性的关系热力学第二定律中的熵增原理与系统的可逆性密切相关。
对于一个可逆过程,系统经历的熵增为零,即ΔS = 0。
这是因为可逆过程不会产生任何排除模式或混乱的行为,系统的熵保持不变。
而对于非可逆过程,系统经历的熵增为正,即ΔS > 0。
这意味着非可逆过程总是趋向于增加系统的混乱程度,使系统的熵增加。
熵可以看作是系统有序度的度量,而熵增则意味着系统的有序度减少。
物理化学03章_热力学第二定律-2-

Helmholtz自由能
Helmholtz(Hermann von Helmholtz, 1821 ~1894 , 德国人)定义了一个状态函数
A def U TS
A 称为Helmholtz自由能(Helmholtz free energy),是 状态函数,具有容量性质。
则 W dA
即:在等温过程中,封闭系统对外所作的功等 于或小于系统Helmholtz自由能的减少值。
而热不能无条件地全变为功
热和功即使数量相同,但“质量”不等, 功是“高质量”的能量
高温热源的热与低温热源的热即使数量相 同,但“质量”也不等,高温热源的热“质量” 较高,做功能力强。
从高“质量”的能贬值为低“质量”的能 是自发过程。
§3.9 热力学第二定律的本质和熵的统计意义
热力学第二定律的本质
热与功转换的不可逆性 热是分子混乱运动的一种表现,而功是分子 有序运动的结果。 功转变成热是从规则运动转化为不规则运动, 混乱度增加,是自发的过程; 而要将无序运动的热转化为有序运动的功就 不可能自动发生。
总结 至此,熵判据问题已经彻底解决。
历史的回顾 实践总结: 发现自发过程共性
发现
第二定率: 解决了过程可能与否,难度大
定量化
Clausius不等式:
计算S和
δQ T
,不方便
Q=0
熵增加原理: 只能判断是否可逆,不理想
孤立系统
熵增加原理(namely, entropy criterion):
由S确定方向和限度,解决问题方便
Gibbs自由能判据
(dG)T , p,Wf 0
0
" "表示可逆,平衡 " "表示不可逆,自发
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 热寂论
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 热寂论
Physical Chemistry University of Science and Technology Beijing
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 非平衡态热力学(超纲)
非平衡态热力学的提出解决了这一矛盾:
Onsager—倒易关系获得1968诺贝尔奖 Prigogine—耗散结构理论1977诺贝尔奖
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 波尔兹曼分布
Physical Chemistry University of Science and Technology Beijing
1. 热力学几率与数学几率不同,数学几率总是小于1,而热力学几率总是大于1;
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 热力学概率
1 1 当盒中有10个球: P ( )10 2 1024
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 热力学概率
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 热力学概率
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 热力学概率
分布情况: 1个球 Ω=2=21 P左=1/2 P右=1/2
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 有序和混乱 做八宝粥的原料
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 非平衡态热力学(超纲)
经典热力学:孤立体系自发消除差别,趋向均匀,从有序 到无序方向进行; 达尔文进化论:生物进化是从单细胞到多细胞,从无序到 有序的方向演变,只要外界条件合适,可以保持非平衡态 而不趋向于平衡态。因此,趋向平衡,趋向无序并非自然 界的普遍规律。
熵值的大小通常有如下规律: (1)对同一物质,当温度升高时,它的运动越
激烈,混乱越大,熵值越大;
(2)同一物质,气、液、固态相比,混乱度递 减,S(g)>S(l) > S(s)。 (3)一般来说,一种分子中,原子数目越多, 混乱度越大,熵值越大;
(4)对气相反应,分解反应由于质点数目增多
而混乱度加大,熵值加大。
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 功与热转换的不可逆性
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 功与热转换的不可逆性
Physical Chemistry University of Science and Technology Beijing
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 第二定律的本质 综上分析,对于同一个体系,发生同一个 过程,从微观上看混乱度增加,从宏观上 看熵值增大,因此我们肯定熵函数和混乱 度是有一定联系的。实际上熵函数可以作 为体系混乱度的一种量度,这就是热力学 第二定律所阐明的不可逆过程的本质。
当盒中有20个球: 小球的数目越多,集中在 一侧的可能性越小,当小 球的数量增加到宏观体系 的数时,小球全部集中在 一侧的可能性几乎是零。
1 20 1 P( ) 6 2 10
一种相反的情况,粒子数目越多,均匀分布的微观状态 数迅速增加,当粒子数目达到宏观体系时,均匀分布的微观状 态数非常非常大,P≈1。因此,对于大量分子的集合体来说, 均匀分布可以代替体系的所有分布。我们平时所观察到的宏观 热力学状态就是由这种均匀分布所表现出来的性质而决定的。
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 热力学概率
N2
O2
可证明均匀分布时系统所具有的微观状态数最 大,即混乱度最大
Physical Chemistry University of Science and Technology Beijing
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 热力学概率
热力学概率就是实现某种宏观状态的微观 状态数,通常用 表示。 数学概率是热力学概率与总的微观状态数 之比,通常用 p 来表示。
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 熵流的简介(超纲)
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 波尔兹曼分布 由玻兹曼公式可看出,混乱度越 大,熵值越大,所以熵是体系混乱度 的量度,这就是熵的物理意义。
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 波尔兹曼分布
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 波尔兹曼分布
Physical Chemistry University of Science and Technology Beijing
,波尔兹曼在1867年就注意到生物体生长过程与熵增加
过程相抗拒的事实,他说,生物为了生存而作一般斗争 ,即不是为了物质,也不是为了能量,而是为了熵。
薛定鄂说过“生物体是吃负熵流长大的”,如果生物 体不能从外界吃进负熵流,那么其内部不断产生的正熵
diS (由血液流动、扩散、生化反应等不可逆过程所引
起)将使它趋向于熵极大的危险状态,那就是死亡。
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 熵流的简介(超纲)
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 熵流的简介(超纲)
deS < 0也称负熵流,它对于生物体的生存是非常重要的
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 熵流的简介(超纲)
Physical Chemistry University of Science and Technology Beijing
2个球
3个球 4个球
Ω=4 =22
Ω=8=23 Ω=16=24 Ω=2 N
P左=1/4
P左=1/8 P左=1/16
P右=1/4
P右=1/8 P右=1/16 P=(1/2)N
(两球都在左)(两球都在右) (三球都在左) (三球都在右) (四球都在左) (四球都在右) 都集中在一侧的数学几率
结论: 2. 粒子数目越多,全部集中在一侧的可能性越小; 3. 粒子数目越多,均匀分布的微观状态数越多。
Physical Chemistry University of Science and Technology Beijing
3 热力学第二定律 3.5 第二定律的本质与熵的统计意义 பைடு நூலகம்熵流的提出(超纲)
热力学第二定律表明,自然界的任何一个孤立体 系总是朝着从有序到无序的方向进行变化,而在 一个孤立体系中,从无序到有序的转化是不会自 动发生的。在变化过程中,孤立体系的熵在不断 增加(能量不变),到体系达平衡时,熵最大。 然而,这个结论与我们所观察到的现实世界中的 某些现象是矛盾的,因为自然界的许多现象总是 朝着更加有序的方向演变,只要外界条件合适, 可以保持非平衡态而不趋向于平衡态。因此,趋 向平衡,趋向无序并非自然界的普遍规律。
