初中数学之阴影部分面积
初中数学阴影面积答题技巧

初中数学阴影⾯积答题技巧 对于⼀些简单求阴影部分⾯积的题⽬,其基本思路是寻找阴影部分图形与规则图形之间的关系,然后利⽤⾯积和差进⾏计算即可. 但有些题⽬是⽆法直接利⽤和差求解的,必须要对图形进⾏观察分析,选择适当的⽅法进⾏计算,下⾯是⼩编为⼤家整理的关于初中数学阴影⾯积答题技巧,希望对您有所帮助。
欢迎⼤家阅读参考学习! 1初中数学阴影⾯积答题技巧 所谓分割策略,⼜称“化整为零”,是将⼀个图形分割成若⼲个有逻辑联系的、较简单或较熟悉的、能够应⽤基本公式进⾏⾯积计算的图形,从⽽解答阴影图形的⾯积的策略。
分割策略是解答“阴影⾯积问题”的最重要的策略。
理论上,中⼩学中的任何图形都可分割为若⼲三⾓形和扇形,因⽽都是可⽤公式进⾏计算的。
在实践中,分割策略⼀般具有两种功能:(1)为利⽤⼏何性质和定理进⾏补整或拼图创造条件;(2)为图形之间的转换创造条件。
在具体运⽤分割策略时,⼀般按照由外到内、由⼤到⼩的次序进⾏分割,以实现规则图形的最⼤化,减⼩计算量。
例2.△ABC为⼀住宅区的平⾯⽰意图,其周长为800m,计划把住宅区外5m内(图2中△ABC与三段圆弧和分别与之相切的三条公切线所围成的阴影部分)作为绿化带,求此绿化带的⾯积。
分析:作为⼀个整体,阴影图形(绿化带)的⾯积很难直接求出,根据题⽬中“圆弧”、“相切”等信息,可以运⽤分割策略,将阴影图形分割为三个矩形和三个扇形。
然后再运⽤“补整策略”将三个扇形合并为⼀个圆,将三个矩形合并为以△ABC周长800m为边,5m为⾼的矩形。
于是,S阴影=S圆+S矩形。
2初中数学⼏何做辅助线技巧 辅助线在平⾏四边形中的恰当运⽤ 平⾏四边形主要包括正⽅形、菱形,以及矩形,这些图形的两组对边、对⾓等具有的性质都有⼀定的相似之处,所以,辅助线在这些图形中的添加⽅法⼀般都具有较⼤的相似性,往往都是为了实现线段的垂直与平⾏,在此基础上构成相应的全等、相似三⾓形。
通常情况下,都是平移、连接图形对⾓线,或者是结合实际情况连接其中⼀边的中点与顶点等⽅式,从⽽将平⾏四边形巧妙转化成相应的矩形、三⾓形等图形,这样再分析解决其该题⽬则更加便捷。
初中数学专题辅导:阴影面积求法9种方法(不规则图形)
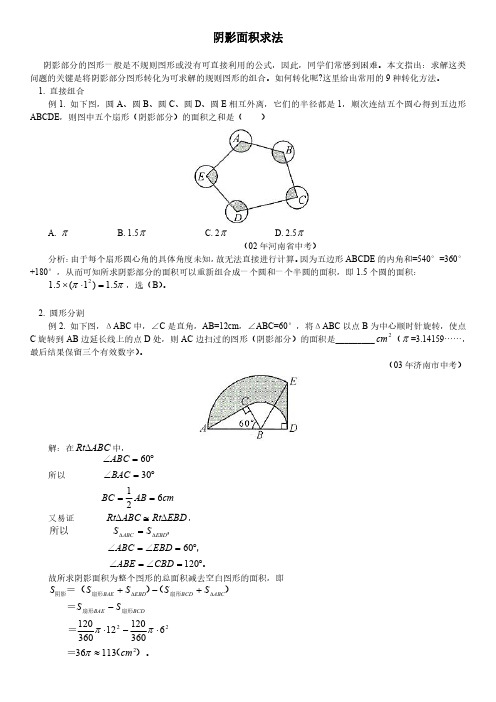
阴影面积求法阴影部分的图形一般是不规则图形或没有可直接利用的公式,因此,同学们常感到困难。
本文指出:求解这类问题的关键是将阴影部分图形转化为可求解的规则图形的组合。
如何转化呢?这里给出常用的9种转化方法。
1.直接组合例1.如下图,圆A 、圆B 、圆C 、圆D 、圆E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是()A.π B.1.5π C.2πD.2.5π(02年河南省中考)分析:由于每个扇形圆心角的具体角度未知,故无法直接进行计算。
因为五边形ABCDE 的内角和=540°=360°+180°,从而可知所求阴影部分的面积可以重新组合成一个圆和一个半圆的面积,即1.5个圆的面积:ππ5.1)1(5.12=⋅⨯,选(B )。
2.圆形分割例2.如下图,ΔABC 中,∠C 是直角,AB=12cm ,∠ABC=60°,将ΔABC 以点B 为中心顺时针旋转,使点C 旋转到AB 边延长线上的点D 处,则AC 边扫过的图形(阴影部分)的面积是_________2cm (π=3.14159……,最后结果保留三个有效数字)。
(03年济南市中考)解:在ABC Rt ∆中,所以cm AB BC BAC ABC 6213060==︒=∠︒=∠又易证EBD Rt ABC Rt ∆≅∆,。
,,所以︒=∠=∠︒=∠=∠=∆∆12060CBD ABE EBD ABC S S EBD ABC 故所求阴影面积为整个图形的总面积减去空白图形的面积,即)。
(===)()=(扇形扇形扇形扇形阴影22211336636012012360120cm S S S S S S S BCDBAE ABC BCD EBD BAE ≈⋅-⋅-+-+∆∆πππ3.平移例3.如下图,矩形内有两个相邻的正方形,面积分别为4和2,那么阴影部分的面积为________________。
史上最全几何阴影面积的解法(1)

【史上最全】初中数学几何阴影面积的3种解法|知识点
初中备考指南1周前
为所有考生和家长,加油!
栏目导语:这是小许老师精心设计的初中知识点学习板块,以语数外基础和提高性考点为主,也会有物化,史政生地等科目知识点合集。
在这里你会对未学提前了解,对已学知识有更好的理解,欢迎转发,收藏!
“几何”问题不仅是初中数学的重点,到了高中数学学习中也占很大比重,内容是循序渐进的,所以基础一定要打好。
这里,就来具体说说如何把这类题的分数拿到手,更准确地说就是初中生要掌握3个方法,才能够解决大部分求解几何图形阴影面积的题目。
公式法
这属于最简单的方法,阴影面积是一个常规的几何图形,例如三角形、正方形等等。
简单举出2个例子:
和差法
攻略一直接和差法
这类题目也比较简单,属于一目了然的题目。
只需学生用两个或多个常见的几何图形面积进行加减。
攻略二构造和差法
从这里开始,学生就要构建自己的数学图形转化思维了,学会通过添加辅助线进行求解。
割补法
割补法,是学生拥有比较强的转化能力后才能轻松运用的,否则学生看到这样的题目还是会无从下手。
尤其适用于直接求面积较复杂或无法计算时,通过对图形的平移、旋转、割补等,为利用公式法或和差法求解创造条件。
攻略一全等法
攻略二对称法
攻略三平移法
攻略四旋转法
距离中考越来越近,希望家长不要再给孩子压力,同时还要开导孩子,中考只是一场普通的考试。
希望同学们也能平时练习要严谨,中考考场放轻松,祝所有同学考个好成绩。
2021年九年级数学初中几何圆、扇形、弓形的面积及阴影部分面积专项

初中几何圆、扇形、弓形的面积及阴影部分面积专项一、圆的面积计算公式:S=R 2,圆心角是1°的扇形面积等于圆面积的1360,圆心角是n 度的扇形面积等于圆的面积的360n ,扇形的弧长等于l=180n R ,⇒S 扇=12lR 。
二、运用公式法、割补法、拼凑法、等积变化法、平移法、旋转法、构造方程法等方法求组合图形的面积。
三、运用割补法、平移法、旋转法、等积变换法、容斥原理求阴影部分面积。
1、弓形面积弓形的面积可以转化为扇形的面积与三角形的面积之差,如下图所示,弓形AmB 的面积S弓形=S 扇性AOB -S △AOB弓形的面积可以转化为:扇形的面积与三角形的面积之和,如下图所示弓形AmB 的面积S 弓形= S 扇性AOB +S △AOB注:①当弓形所含的弧是劣弧时如甲图所示,弓形AmB 的面积S 弓形=S 扇性AOB -S △AOB②当弓形所含的弧是优弧时,如图乙所示,AnB 的面积S 弓形= S 扇性AOB +S △AOB③当弓形所含的弧是半圆时,弓形的面积S 弓形=12S 圆 如图:半径OA=6cm,C 为OB 的中点,∠AOB=120°,求阴影部分面积S 。
(右:乙图)解:由图形可知,S 阴影ABC =S 扇性ABO -S △ACO ,而S 扇形ABO =21206360⋅=12,S △ACO =12×6×3×sin60°=932,所以S 阴影ABC =(93122-)cm 2。
2、割补法凡求与圆有关的不规则图形面积问题,一般都要把它转化为三角形、扇形、弓形的面积来求解,在进行复杂的图形的面积计算时,时常通过添加辅助线,把图形分割成若干个基本图形求解,这种求解的方法是经常用到的。
如图:⊙O 中的弦AC=2cm ,圆周角∠ABC=45°,求图中阴影部分的面积。
(部分与整体)解:做⊙O 的直径AB 1,则连结OC 、B 1C ,∠ACB=90°,∠B=∠B 1,AB 1=22,∵OA=2,∴S △AOC=1,S 扇形AOC =12,∴S 阴影=S 扇形AOC -S △AOC =12-1 例二:如图在两个半圆中大圆的弦MN 与小圆相切,D 为切点,且MN ∥AB ,MN=a ,ON ,CD 分别为两圆的半径,求阴影部分的面积。
求阴影部分面积九字决

求阴影部分面积九字决河北张家口市第十九中学 贺峰关于求几何图形阴影部分面积的计算问题是初中数学“空间与图形”中一道亮丽的风景,历年来常考不衰,这类试题往往将多边形与圆结合,并且多由一些不规则图形组合、重叠而成;既能考查同学们观察能力、分析能力、计算能力、空间想象能力,同时又能考查同学们合理选择和运用数学思想方法的技能。
解决这类问题时,要善于抓住图形的特点,灵活采用作“差”、重“组”、“去”重、求“和”巧“移”、“翻”折、旋“转”、“设”参、转“化”等方式进行,从而使问题得到解决。
一、作“差”例1如图1,正六边形ABCDEF 的边长是a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是( )(A)223332a ⎪⎪⎭⎫ ⎝⎛π- (B)23333a ⎪⎪⎭⎫ ⎝⎛π-(C)232233a ⎪⎪⎭⎫⎝⎛-π (D)23223a ⎪⎭⎫ ⎝⎛π- 析解:依题意,由于给出的阴影部分是由规则图形围成的,因此解决此题可利用“作差法”解决,即S 阴影=S 正六边形-2S 扇形=232233a ⎪⎪⎭⎫⎝⎛-π。
因此答案选C 。
二、重“组”例2 如图2,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连接五个圆心得到五边形ABCDE ,则图中五个扇形的面积和是_______。
析解:由于不知道每个扇形圆心角的具体角度,故无法直接计算,而五边形的内角和为5400=3600+1800,因此可将阴影部分的面积“重新组合”成一个圆和一个半圆的面积,即1.5个圆的面积。
因此结果为1.5π。
三、“去”重例3(2005湖北武汉) 如图3,Rt △ABC 中,∠C=900,AC =2,AB =4,分别以AC 、BC 为直径作半圆,则图中阴影部分的面积为 。
析解:观察图形,发现两个半圆覆盖了一个三角形,而且中间阴影部分重叠了两次,故采用“图形去重法”解决,即阴影部分的面积等于大、小半圆面积之和与Rt △ABC 面积的差:12×π×12+12×π×(42-22÷2)2-12×2×3,故结果为2π-23。
阴影部分面积的多种求法

阴影部分面积的多种求法陕西延安市新区第一中学(716000)陈巧莲[摘要]求阴影部分面积,一方面考查了学生的基础知识、基本能力和基本方法,另一方面考查了学生观察分析能力、空间想象能力和运算能力.文章结合典型例题,提出求解阴影部分面积的方法:公式法、直接和差法、构造和差法、平移法、旋转法.[关键词]阴影部分;面积;求法[中图分类号]G 633.6[文献标识码]A[文章编号]1674-6058(2021)05-0027-02平面图形的面积计算问题是常见的数学题型,其中较难的是求平面图形阴影部分的面积,这类问题构思巧妙,属于综合类试题.其一方面考查了学生的基础知识、基本能力和基本方法,另一方面考查了学生的观察分析能力、空间想象能力和运算能力.一般所求阴影部分的图形为不规则图形,在解题时需进行分解组合,将不规则图形转化为规则图形.一、公式法某些阴影部分的图形是规则图形,求面积时可直接应用公式计算,如:S 三角形=12ah ,S 平行四边形=ah ,S 矩形=ab ,S 菱形=ah =12×对角线的乘积,S 正方形=a 2,S 扇形=n πr 2360,等等.[例1]如图1,在矩形ABCD 中,AB =3,AD =6,将AD 边绕点A 顺时针旋转,使点D 恰好落在BC 边上的点D '处,则阴影部分的面积为().图1A .9B.3πC .9πD .18分析:∵线段AD '由线段AD 旋转而成,AD =6,∴AD '=AD =6.∵AB =3,∠B =90°,∴∠AD 'B =30°.∵AD ∥BC ,∴∠DAD '=∠AD 'B =30°,∴S 阴影=30×π×62360=3π.故选B .评注:本题平面图形的阴影部分是一个扇形,欲求扇形面积,需求得扇形圆心角的度数和半径长,然后直接利用扇形面积公式求解.分析出阴影部分是什么样的图形是求解问题的关键.二、直接和差法某些阴影部分,虽然是不规则图形,但是可直接看出它是哪些图形的和或差,无须作辅助线,这样就可以分别求出各个图形的面积,然后再求和或作差.[例2]如图2,在Rt△ACB 中,∠C =90°,AC =BC =2,点D 是AB 的中点,DE 是以点A 为圆心,以AD 为半径的弧, DF 是以点B 为圆心,以BD 为半径的弧,则图中由 DE 、 DF 、EC 、FC 围成的阴影部分的面积为.图2分析:在Rt △ABC 中,∵∠C =90°,AC =BC =2,∴AB =22,∠A =∠B =45°,∵D 是AB 的中点,∴AD =DB =2,∴S 阴影=S △ABC -2S 扇形ADE =12×2×2-2×45×π×(2)2360=2-π2,故答案为2-π2.评注:此题可直接看出阴影部分面积等于三角形面积减去两个扇形的面积.当然,某些阴影部分图形面积可能是若干个图形面积的和,或和与差的组合.这里实际上将一个问题转化为三个小问题,从而达到解决问题的目的.三、构造和差法某些阴影部分,从已知图形中无法看出它是哪些图形的和或差,需要作辅助线才能看出来,此时应使用构造和差法,通过辅助线,补上一些规则图形,再减去其他规则图形,从而达到化不规则图形为规则图形的目的.[例3]如图3,在扇形OAB 中,C 是OA 的中点,CD ⊥OA ,CD 与AB 交于点D ,以O 为圆心,OC的长为半径作CE 交OB 于点E ,若OA =4,∠AOB =120°,则图中阴影部分的面积为.(结果保留π)图3图4分析:如图4,连接OD ,AD ,∵点C 为OA 的中点,∴OC =12OA =12OD ,∵CD ⊥OA ,∴∠CDO =30°,数学·解题研究∠DOC=60°,∴△ADO为等边三角形,∴CD=23,∴S扇形AOD=60×π×42360=83π,∴S阴影=S扇形AOB-S扇形COE-(S扇形AOD-S△COD)=120×π·42360-120×π·22360-()83π-12×2×23=163π-43π-83π+23=43π+23.故答案为43π+23.评注:需注意的是,在有弧线的图形中,通常会用扇形面积公式,此题还用到了等边三角形的判定、直角三角形的性质等,综合性比较强,不要把它看成只是求面积这样简单的问题,这样的题常作为压轴题,有一定的难度.四、平移法某些阴影部分的图形虽是不规则图形,但是通过将一部分图形平移,可以拼合成规则的图形,这是利用了图形平移后,图形的形状、大小都未变,只是位置变化的性质.一个图形平移后能否与另一个图形重合,主要看几个关键点按相同的方法平移后能否与对应点重合.[例4]如图5,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线,使其顶点P沿直线移动到点P'(2,-2),点A的对应点为A',则图中抛物线上AP段、A'P'段、P P'、A A'围成的图形(阴影部分)面积为.图5图6分析:如图6,连接AP,A'P',过点A作AD⊥PP'于点D,由题意可得出AP∥A'P',AP=A'P',∴四边形APP'A'是平行四边形,∵抛物线的顶点为P(-2,2),与y轴交于点A(0,3),平移该抛物线使其顶点P沿直线移动到点P'(2,-2),∴PO=22+22=22,PP'=22×2=42,∠AOP=45°,又∵AD⊥OP,是等腰直角三角形,∴AD=DO=sin45°·OA=×3=322,∴抛物线上AP段扫过的区域(阴影部分)的面积=平行四边形APP'A'的面积=42×322=12.故答案为12.评注:抛物线也是图形,平移后其形状与大小都不变,所以图中弓形AP与弓形A'P'的形状与大小是相同的;图形平移后形成平行四边形,注意平行四边形面积公式的使用.五、旋转法某些阴影部分的图形虽是不规则图形,但是将其中的一部分图形旋转后,可以拼接成规则图形,这是利用旋转后的图形其形状、大小不变,只是位置变化的性质.一个图形旋转后能否与另一个图形重合,主要看几个关键点按相同的旋转方法旋转后能否与对应点重合.[例5]如图7,AC是汽车挡风玻璃前的雨刷器,如果AO=45cm,CO=5cm,当AC绕点O顺时针旋转90°时,则雨刷器AC扫过的面积为cm2(结果保留π).图7分析:∵OA=OA',OC=OC',AC=A'C',∴△AOC≌△A'OC',∴雨刷器AC扫过的面积=S扇形AOA'-S扇形COC'=452-524×π=500π(cm2),故答案为500π.评注:此题相当于将一个三角形旋转后,求边AC扫过的面积.通过上述试题我们发现,它实际上是两个扇形面积的差,这是中考的高频题型.求阴影部分图形的面积,本质就是将不规则图形转化为规则图形,转化的方法有直接和差法、构造和差法、平移法、旋转法、对称法、等积替代法、覆盖法等,然后结合已知数量,将几何问题转化为代数运算.这是始终不变的主线.[参考文献][1]于秀坤.求阴影部分面积的思路和方法[J].中学生数理化(初中版·中考版),2020(8):2-3.[2]王金伟.求阴影部分面积的方法技巧[J].数理天地(初中版),2019(10):12-13.[3]罗峻,段利芳.十招走出圆中面积阴影[J].数理化学习(初中版),2019(7):29-33.[4]王文智.利用对称性求解与扇形相关的阴影面积[J].理科考试研究,2019(10):27-28.(责任编辑陈昕)数学·解题研究。
求阴影部分面积教学设计-冀教版九年级数学
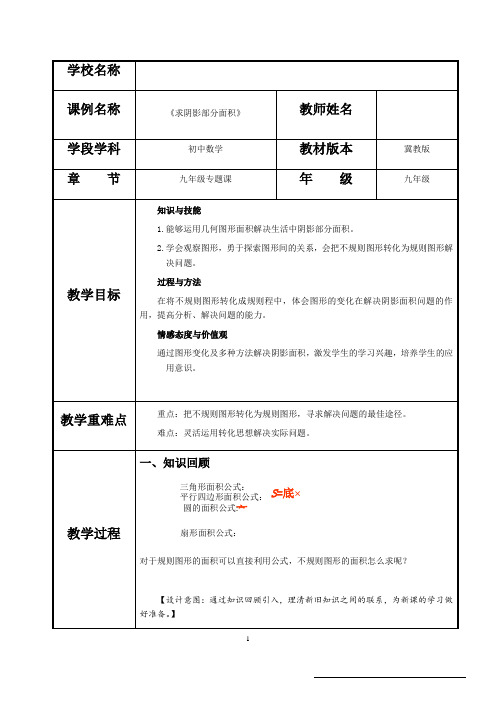
学校名称课例名称 《求阴影部分面积》教师姓名学段学科 初中数学 教材版本 冀教版 章 节九年级专题课年 级九年级教学目标知识与技能1.能够运用几何图形面积解决生活中阴影部分面积。
2.学会观察图形,勇于探索图形间的关系,会把不规则图形转化为规则图形解决问题。
过程与方法在将不规则图形转化成规则程中,体会图形的变化在解决阴影面积问题的作用,提高分析、解决问题的能力。
情感态度与价值观通过图形变化及多种方法解决阴影面积,激发学生的学习兴趣,培养学生的应用意识。
教学重难点重点:把不规则图形转化为规则图形,寻求解决问题的最佳途径。
难点:灵活运用转化思想解决实际问题。
教学过程一、知识回顾对于规则图形的面积可以直接利用公式,不规则图形的面积怎么求呢?【设计意图:通过知识回顾引入,理清新旧知识之间的联系,为新课的学习做好准备。
】三角形面积公式:平行四边形面积公式: S =底×高圆的面积公式:扇形面积公式:【板书课题】专题课:阴影部分的面积二、探究新知、形成共识1、公式法所求阴影部分的面积是规则图形,直接用几何图形的面积公式求解.lR R n S 213602==π扇形2、割补法先设法将不规则阴影部分与空白部分组合,构造规则图形或分割后为规则图形,再进行面积和差计算.圆阴影S S 41=ABC S S S ∆-=圆阴影41例题讲解:要在面积为1256m2的三角形广场ABC 的三个角处各建一个半径相同的扇形草坪,要求草坪总面积为广场面积的一半,那么扇形的半径应是多少?【设计意图:运用几何画板动画助力教学,使抽象问题具体化,帮助学生直观理解如何进行图形的拼接,发展学生的空间观念。
】针对练习:3、等积转化法通过对图形的变换,为利用公式法或和差法求解创造条件.圆阴影S S 21= 圆阴影S S 41=例题讲解:将四边形ABCD 绕顶点A 顺时针旋转45°至四边形AB ′C ′D ′的位置,若AB =16 cm ,则图中阴影部分的面积为 ( )cm ².=S阴影思路总结:如图在矩形ABCD 中,AB=2,AD=4,将AD 边绕点A 顺时针旋转,使点D 正好 落在BC 边上的点D ′处,则阴影部分的扇形面积为________________.【设计意图:通过学生合作探究,找到解决图形变化的方法,将不规则图形转化为规则,并用和差求解,在此活动中体验数学建模,培养学生与人合作交流的能力,增强学生探究能力,操作能力,分析问题能力,发展空间观念。
与圆有关的计算——求阴影部分面积

㊀㊀㊀解题技巧与方法125㊀数学学习与研究㊀2023 04与圆有关的计算与圆有关的计算㊀㊀㊀ 求阴影部分面积Һ王㊀玮㊀(十堰市东风第五中学,湖北㊀十堰㊀442000)㊀㊀ʌ摘要ɔ面积问题是初中数学中的常见题型,与圆有关的求阴影部分面积问题是这类问题中的一个难点,通常不规则的阴影图形的面积是由三角形㊁四边形㊁扇形㊁圆和弓形等基本图形组合而成的,学生在解决问题时需要观察图形特点,会分割或组合图形.ʌ关键词ɔ计算;阴影部分面积在近几年的中考试题中,求阴影部分的面积是一个热点.观察㊁分析图形可知,阴影部分通常是由三角形㊁四边形㊁扇形和圆等常见的几何图形组成的.学生在解决问题时首先要明确需要计算面积的阴影部分是由哪些图形分解或组合而成的,才能找到解题的途径.下面将求阴影部分面积的常见方法总结如下.类型一:直接公式法例1㊀如图1,矩形ABCD的边长AB=1,BC=2.把BC绕B逆时针旋转,使C恰好落在AD上的点E处,线段BC扫过部分为扇形BCE,则扇形BCE的面积是.图1ʌ分析ɔ根据矩形的性质得出ADʊBC,øA=90ʎ,易得øEBC=øAEB=30ʎ,再根据扇形的面积公式求出即可.例2㊀如图2,在等腰直角三角形ABC中,øA=90ʎ,BC=4.分别以点B㊁点C为圆心,线段BC长的一半为半径作圆弧,交AB,BC,AC于点D,E,F,则图中阴影部分的面积为.ʌ分析ɔ阴影部分的面积S=SәABC-S扇形BDE-S扇形CEF.图2例3㊀如图3,在▱ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F,若øBAC=60ʎ,øABC=100ʎ,BC=4,则扇形EBF的面积为.图3ʌ分析ɔ先根据三角形内角和定理求出øACB,再根据三角形外角的性质求出øBEF,最后根据扇形面积公式直接计算即可.例4㊀如图4,AB是☉O的直径,CD是弦,øBCD=30ʎ,OA=2,则阴影部分的面积是.图4ʌ分析ɔ先根据圆周角定理得到øBOD=60ʎ,然后根据扇形的面积公式计算阴影部分的面积即可.类型二:直接和差法阴影部分面积可由扇形㊁三角形㊁特殊四边形的面积相加减得到.㊀图5例5㊀如图5,在扇形OAB中,已知øAOB=90ʎ,OA=2,过AB(的中点C作CDʅOA,CEʅOB,垂足分别为D,E,则图中阴影部分的面积为.ʌ分析ɔ先根据矩形的判定定理得到四边形CDOE是矩形,再连接OC,根据全等三角形的性质得到OD=OE,得到矩形CDOE是正方形,最后根据扇形和正方形的面积公式即可得到结论.图6例6㊀如图6,在菱形ABCD中,对角线AC,BD交于点O,øABC=60ʎ,AB=2,分别以点A㊁点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为.ʌ分析ɔ先根据菱形的性质得到ACʅBD,øABO=12øABC=30ʎ,øBAD=øBCD=120ʎ,再根据直角三角形的性质求出AC,BD的长,最后根据扇形面积公式㊁菱形面积公式计算即可.图7例7㊀如图7,在边长为23的正方形OABC中,D为边BC上一点,且CD=2,以O为圆心㊁OD为半径作圆弧,分别与OA,OC的延长线交于点E,F,则阴影部分的面积为.㊀㊀解题技巧与方法㊀㊀126数学学习与研究㊀2023 04ʌ分析ɔ设AB交EF(于M,阴影部分的面积S=S正方形OABC-SәOAM-S扇形ODM-SәOCD.例8㊀如图8,已知四边形ABCD和四边形BEFM均为正方形,以B为圆心㊁BE为半径作弧EM.若大正方形的边长为8,则图中阴影部分的面积为.(结果保留π)图8ʌ分析ɔ根据正方形的性质得出øABC=øDCM=90ʎ,BE=BM=8,AB=BC=CD=AD,设AB=BC=CD=AD=a,则阴影部分的面积S=S扇形BME+S正方形ABCD+SәDMC-SәADE,代入求出即可.类型三:构造和差法阴影部分面积需要通过添加辅助线构造扇形㊁三角形或特殊四边形,然后相加减.图9例9㊀如图9,AB是☉O的直径,CD为☉O的弦,ABʅCD于点E,若CD=63,AE=9,求阴影部分的面积.ʌ分析ɔ根据垂径定理得出CE=DE=12CD=33,再利用勾股定理求得半径,根据锐角三角函数关系得出øEOD=60ʎ,进而结合扇形面积公式即可求出答案.例10㊀如图10,正方形ABCD内接于☉O,PA,PD分别与☉O相切于点A和点D,PD的延长线与BC的延长线交于点E.已知AB=2,则图中阴影部分的面积为.图10ʌ分析ɔ如图10所示,连接AC,OD,根据已知条件得到AC是☉O的直径,øAOD=90ʎ,根据切线的性质得到øPAO=øPDO=90ʎ,易得әCDE是等腰直角三角形,再根据等腰直角三角形的性质得到PE=32,最后根据梯形和圆的面积公式即可求出阴影部分的面积.图11例11㊀如图11,等边三角形ABC的边长为2,以A为圆心,1为半径作圆弧分别交AB,AC边于D,E,再以点C为圆心,CD长为半径作圆交BC边于F,连接E,F,那么图中阴影部分的面积为.ʌ分析ɔ如图11,过A作AMʅBC于M,ENʅBC于N,根据等边三角形的性质得到AM=32BC=32ˑ2=3,求得EN=12AM=32,再根据三角形的面积和扇形的面积公式计算即可.例12㊀如图12,在RtәABC中,øBAC=30ʎ,以直角边AB为直径作半圆交AC于点D,以AD为边作等边三角形ADE,延长ED交BC于点F,BC=23,则图中阴影部分的面积为.(结果不取近似值)图12ʌ分析ɔ如图12,根据题意结合等边三角形的性质分别得出AB,AC,AD,DC的长,进而利用S阴影=SәABC-SәAOD-S扇形ODB-SәDCF求出答案.图13例13㊀如图13,在菱形ABCD中,øD=60ʎ,AB=2,以B为圆心㊁BC长为半径画AC(,点P为菱形内一点,连接PA,PB,PC.当әBPC为等腰直角三角形时,图中阴影部分的面积为.ʌ分析ɔ如图13,连接AC,延长AP交BC于E,根据菱形的性质得出әABC是等边三角形,进而通过三角形全等证得AEʅBC,从而求得AE,PE,则S阴影=S扇形BAC-SәPAB-SәPBC.例14㊀如图14,在әABC中,O为BC边上的一点,以O为圆心的半圆分别与AB,AC相切于点M,N.已知øBAC=120ʎ,AB+AC=16,MN(的长为π,则图中阴影部分的面积为.图14ʌ分析ɔ如图14,连接OM,ON,根据半圆分别与AB,AC相切于点M,N,可得OMʅAB,ONʅAC,由øBAC=120ʎ,可得øMON=60ʎ,进而得出øMOB+øNOC=120ʎ,再根据MN(的长为π,可得OM=ON=r=3,连接OA,根据RtәAON中,øAON=30ʎ,ON=3,可得AM=AN=3,进而可求得图中阴影部分的面积.类型四:等积转化法利用等积转化法将阴影部分面积转化为求扇形㊁三角形㊁特殊四边形的面积或它们面积的和差.㊀㊀㊀解题技巧与方法127㊀数学学习与研究㊀2023 04例15㊀如图15,将半径为2㊁圆心角为90ʎ的扇形BAC绕点A逆时针旋转60ʎ,点B,C的对应点分别为D,E,点D在AC(上,则阴影部分的面积为.图15ʌ分析ɔ如图15,连接BD,直接利用旋转的性质结合扇形面积求法及等边三角形的判定与性质得出S阴影=S扇形BAC-S弓形AD=S扇形BDC+SәADB,进而得出答案.例16㊀如图16,在әABC中,CA=CB,øACB=90ʎ,AB=2,点D为AB的中点,以点D为圆心作圆心角为90ʎ的扇形DEF,点C在弧EF上,则图中阴影部分的面积为.图16ʌ分析ɔ如图16,连接CD,证明әDCHɸәDBG,则S四边形DGCH=SәBDC,求得扇形FDE的面积,则阴影部分的面积即可求得.例17㊀如图17,AB是半圆O的直径,线段DC是半圆O的弦,连接AC,OD,若ODʅAC于点E,øCAB=30ʎ,CD=3,则阴影部分的面积为.图17ʌ分析ɔ如图17,连接OC,先证得әCOD是等边三角形,然后证得RtәAOEɸRtәCOE,即可得出S阴影=S扇形OCD.㊀图18例18㊀如图18,在边长为4的正方形ABCD中,以AB为直径的半圆交对角线AC于点E,以C为圆心㊁BC长为半径画弧交AC于点F,则图中阴影部分的面积是.ʌ分析ɔ如图18,连接BE,易证S弓形AE=S弓形BE,ʑ图中阴影部分的面积=S半圆-12(S半圆-SәABE)-(SәABC-S扇形CBF).类型五:容斥原理法当阴影部分是由几个图形叠加形成时,求阴影部分面积需先找出叠加前的几个图形,然后厘清图形之间的重叠关系.计算方法:叠加前的几个图形面积之和-(多加部分面积+空白部分面积).例19㊀如图19,直径AB=6的半圆,绕B点顺时针旋转30ʎ,此时点A到了点Aᶄ处,则图中阴影部分的面积为.图19ʌ分析ɔȵ半圆绕B点顺时针旋转30ʎ,ʑS阴影=S半圆+S扇形BAAᶄ-S半圆=S扇形BAAᶄ.例20㊀如图20,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把әOAC绕点A按顺时针方向转到әOᶄACᶄ的位置,使得点Oᶄ的坐标是(4,43),则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为.图20ʌ分析ɔ如图20,过Oᶄ作OᶄMʅOA于M,解直角三角形求出旋转角的度数,根据图形得出阴影部分的面积S=S扇形AOOᶄ+SәOᶄACᶄ-SәOAC-S扇形ACCᶄ=S扇形AOOᶄ-S扇形ACCᶄ,分别求出即可.㊀图21例21㊀如图21,在矩形ABCD中,AB=6,BC=4,以A为圆心㊁AD长为半径画弧交AB于点E,以C为圆心㊁CD长为半径画弧交CB的延长线于点F,求图中阴影部分的面积.ʌ分析ɔ图中阴影部分的面积=S扇形CFD-(S矩形ABCD-S扇形ADE).㊀图22例22㊀如图22,在扇形OAB中,øAOB=120ʎ,连接AB,以OA为直径作半圆C交AB于点D,若OA=4,则图中阴影部分的面积为.ʌ分析ɔ如图22,连接OD,CD,根据圆周角定理得到ODʅAB,根据等腰三角形的性质得到AD=DB,øOAD=30ʎ,再根据扇形面积公式㊁三角形的面积公式计算即可.阴影部分的面积S=S扇形OAB-SәAOB-(S扇形CAD-SәACD).ʌ参考文献ɔ[1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.[2]章士藻.中学数学教育学[M].北京:高等教育出版社,2007.[3]曹一鸣,冯启磊,陈鹏举,等.基于学生核心素养的数学学科能力研究[M].北京:北京师范大学出版社,2017.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学之阴影部分面积
一、直接法
1、如图1,在Rt △ABC 中,∠ABC=90°,AB=8cm,BC=6cm,分别以A 、C 为圆心,
以
2
AC 为半径作圆,将Rt △ABC 截去两个扇形,则剩余(阴影)部分的面积为( )cm 2
A 、24-π425
B 、π425
C 、24-π4
5 D 、24-π625
2、如图2,将△ABC 绕点B 逆时针旋转到△A 1BC 1使A 、B 、C 1在同一直线上,
若∠BCA=90°,∠BAC=30°,AB=4cm,则图2中的阴影部分面积为 cm 2
3、如图3,正方形的边长为a ,以各顶点为圆心,2
1
a 为半径画弧。
再以正方形的中心
为圆心,2
1
a 为半径画圆,则阴影部分的面积等于
二、割补法
4、如图4,△ABC 是直角边长为a 的等腰直角三角形,直角边AB 是半圆O 1的直径, 半圆O 2过C 点且与半圆O 1相切,则图中阴影部分的面积是( )
A 、
2
36
7a π- B 、2365a π- C 、2367a D 、2365a 5、如图5,AB=EF=4cm,BC=AE=3cm,则阴影部分面积为
6、如图6,中的圆均为等圆,且相邻两圆外切,圆心连线构成正三角形,
记各阴影部分面积从左至右依次为S 1,S 2,S 3,…S n ,则S 12:S 4的值等于
三、平移法
7、如图7,平行于y 轴的直线l 被
抛物线y=21x 2+1,y=2
1x 2
-1所截,
当直线l 向右平移3个单位时,
直线l 被两条抛物线所截得的 线段扫过的图形面积为
8、在长为a m,宽为b m 的一块草坪上修一条宽1 m 的笔直小路,
则余下草坪的面积可表示为 m 2
;
现为了增加美感,把这条小路改为宽恒为1 m 的弯曲小路(如图8)
则余下草坪的面积为 m 2
四、对称法
9、如图9,⊙O 的半径为2,C 1是函数y=
21x 2的图象,C 2是函数y= -2
1x 2
的图象, 则阴影部分的面积是
10、如图10,⊙A 和⊙B 都与x 轴和y 轴相切,
圆心A 和圆心B 都在反比例函数y=x
1
图象上,
则图中阴影部分的面积等于
五、旋转法
11、如图11,半圆O 的直径AB=20,将半圆O 绕着点B 顺时针
旋转54°得到半圆O 1,弧A 1B 交AB 于点P (1)求AP 的长;(2)求图中阴影部分的面积(结果精确到0.1)
图
2
1O 图4
图
5
图6
第1个
图11
图3
(参考数据:sin54°=0.81,cos54°=0.59,tan54°=1.38∏,π=3.14)
六、等积法
12、如图12,是重叠的两个直角三角形,将其中一个直角三角形沿BC 方向平移
得到△DEF,如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为 cm 2
13、如图13,四边形ABCD 、CEFG 是正方形,B 、C 、E 在同一直线上,
正方形ABCD 的边长是4,则△BDF 的面积是 。
14、如图14,A 、B 是半圆周上的三等分点,
则阴影部分的面积是 cm 2
七、方程法
15、矩形纸片ABCD 的边长AB=4,AD=2,将矩形纸片沿EF 折叠,使点A 与点C 重合,
折叠后其一面着色如图15,则着色部分的面积为( )A 、8 B 、211 C 、4 D 、2
5
16、如图16,在半径为5,圆心角等于45°的扇形AOB 内部作一个正方形CDEF,使
点C 在OA 上,点D 、E 在OB 上,点F 在弧AB 上,则阴影部分的面积为
八、参数法
17、如图17,E,F,G,H 分别为正方形ABCD 的边
AB,BC,CD,DA 上的点,且AE=BF=CG=DH=
3
1
AB, 则图中阴影部分的面积与正方形ABCD 的面积之比为( ) A 、
52 B 、94C 、21 D 、5
3 九、比例法
18、如图18,点M 是△ABC 内一点,过点M 分别作直线平行于△ABC 的各边,
所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别为4,9和49 则△ABC 的面积是
十、估算法
19、如图19
,是二次函数y= -2
1x 2
+2的图象在x 轴上方的一部分,
对于这段图象与x 轴所围成的阴影部分的面积,
你认为与其最接近的值是( )A 、4 B 、3
16
C 、2π
D 、8
20、如图20,记抛物线y=-x
2
+1的图象与x 正半轴的交点为A ,将线段OA 分成n 等份,
设分点分别为P 1,P 2,…,P n-1,过每个分点作x 轴的垂线,
分别与抛物线交于点Q 1,Q 2,…,Q n-1,再记直角三角形OP 1Q 1,P 1P 2Q 2,…
的面积分别为S 1,S 2,…这样就有S 1=3221n n -,S 2=3
224
n
n -,…记W=S 1+S 2+…+S n-1, 当n 越来越大时,你猜想W 最接近的常数是( )A 、
32 B 、21 C 、31 D 、4
1
图15
O
A
B
C
F
D 图16
A
B
D E
N H M
P
F Q
G 图19
n-1
图20
图12。
