清华大学数学分析真题参考答案
清华大学考研试题及答案
清华大学考研试题及答案模拟试题：清华大学考研数学试题一、选择题（每题3分，共30分）1. 下列函数中，哪个不是周期函数？A. y = sin(x)B. y = e^xC. y = |x|D. y = cos(x)答案：B2. 函数f(x) = x^2 + 3x - 2在区间（-∞，-3]上的单调性是：A. 单调递增B. 单调递减C. 先减后增D. 不确定答案：B3. 已知数列{an}满足a1 = 1，an + 1 = 2an + 1，该数列是：A. 等差数列B. 等比数列C. 既不是等差数列也不是等比数列D. 几何数列答案：C4. 曲线y = x^3 - 6x^2 + 12x + 5在点（2，12）处的切线斜率为：A. -1B. 0C. 1D. 2答案：D5. 以下哪个选项是正确的？A. ∫(0 to 1) x dx = 1/2B. ∫(0 to 1) x^2 dx = 1/3C. ∫(0 t o 1) x^3 dx = 1/4D. 以上都是答案：D6. 方程x^2 - 4x + 3 = 0的根是：A. 1, 3B. -1, 3C. 2, 2D. -2, 2答案：A7. 以下哪个级数是收敛的？A. ∑(1 to ∞) (1/n)^2B. ∑(1 to ∞) (1/n)C. ∑(1 to ∞) (-1)^n / nD. ∑(1 to ∞) n答案：A8. 以下哪个矩阵是可逆的？A. | 1 2 || 2 4 |B. | 1 0 || 0 1 |C. | 2 0 || 0 2 |D. | 0 1 || 1 0 |答案：B9. 设随机变量X服从参数为λ的泊松分布，P(X=k)的表达式为：A. (λ^k / k!) * e^(-λ)B. λ^k / k!C. e^(-λ) * λ^kD. k * (λ^k / k!)答案：A10. 以下哪个命题是错误的？A. 两个连续函数的乘积仍然是连续函数B. 有界数列必有收敛子列C. 闭区间上连续函数必定一致连续D. 以上都是答案：B二、填空题（每题4分，共20分）11. 极限lim (x->0) [sin(x)/x] 的值为 _______ 。
清华大学往年考试试卷真题
清华大学往年考试试卷真题清华大学是中国顶尖的高等学府之一，其考试试卷真题通常包含多个学科领域，以下是一个模拟的清华大学往年考试试卷真题的示例：清华大学数学分析考试试卷一、选择题（每题2分，共20分）1. 下列函数中，哪一个不是连续函数？A. f(x) = x^2B. f(x) = sin(x)C. f(x) = |x|D. f(x) = 1/x2. 函数f(x) = x^3 - 2x + 1在x=1处的导数是：A. 2B. 0C. -2D. 43. 积分∫(0,1) x^2 dx的值是：A. 1/3B. 1/2C. 2/3D. 1...（此处省略其他选择题）二、填空题（每题3分，共15分）1. 函数f(x) = 3x^2 + 2x - 1的极值点是_________。
2. 若f(x) = e^x，那么f'(x) = __________。
3. 函数y = ln(x)的定义域是_________。
...（此处省略其他填空题）三、简答题（每题10分，共30分）1. 证明函数f(x) = x^3在R上是单调递增的。
2. 解释什么是泰勒级数，并给出e^x的泰勒级数展开式。
3. 计算定积分∫(1, e) (x + 1/x) dx。
四、解答题（每题15分，共30分）1. 已知函数f(x) = x^2 - 4x + 4，求其在区间[0, 3]上的最小值。
2. 给定函数g(x) = sin(x) + cos(x)，求其在x=π/4处的导数，并解释其几何意义。
3. 解析下列微分方程：dy/dx = x^2 - y^2，初始条件为y(0) = 1。
五、附加题（10分）1. 讨论函数f(x) = x^3 - 6x^2 + 11x - 6在实数域R上的零点。
注意事项：- 请在答题纸上作答，不要在试卷上直接书写。
- 请保持答题纸整洁，字迹清晰。
- 选择题请用2B铅笔涂黑，填空题和解答题请用黑色签字笔书写。
祝考试顺利！请注意，以上内容仅为模拟示例，并非真实的清华大学考试试卷真题。
(完整word版)清华大学 杨虎 应用数理统计课后习题参考答案3
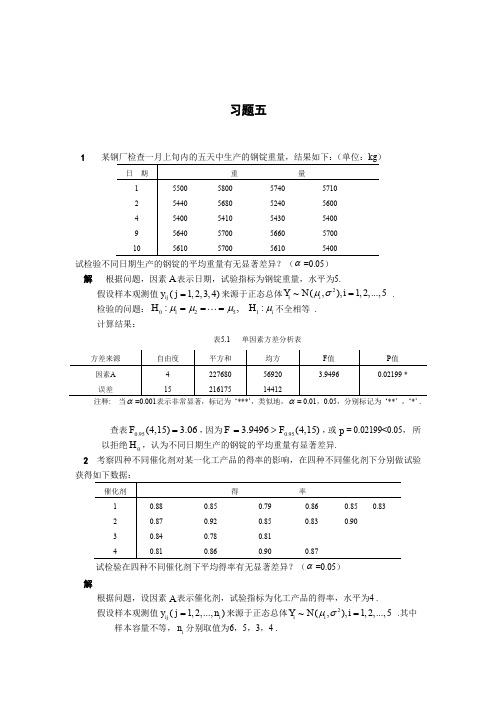
习题五1试检验不同日期生产的钢锭的平均重量有无显著差异？（α=0.05） 解 根据问题，因素A 表示日期，试验指标为钢锭重量，水平为5.假设样本观测值(1,2,3,4)ij y j =来源于正态总体2~(,),1,2,...,5i i Y N i μσ= .检验的问题：01251:,:i H H μμμμ===不全相等 .计算结果：表5.1 单因素方差分析表注释: 当=0.001表示非常显著，标记为 ‘***’，类似地，= 0.01，0.05，分别标记为 ‘**’ ，‘*’ .查表0.95(4,15) 3.06F =，因为0.953.9496(4,15)F F =>，或p = 0.02199<0.05， 所以拒绝0H ，认为不同日期生产的钢锭的平均重量有显著差异.2 考察四种不同催化剂对某一化工产品的得率的影响，在四种不同催化剂下分别做试验 试检验在四种不同催化剂下平均得率有无显著差异？（α=0.05）解根据问题，设因素A 表示催化剂，试验指标为化工产品的得率，水平为4 .假设样本观测值(1,2,...,)ij i y j n =来源于正态总体2~(,),1,2,...,5i i Y N i μσ= .其中样本容量不等，i n 分别取值为6，5，3，4 .检验的问题：012341:,:i H H μμμμμ===不全相等 .计算结果：表5.2 单因素方差分析表查表0.95(3,14) 3.34F =，因为0.952.4264(3,14)F F =<，或p = 0.1089 > 0.05，所以接受0H ，认为在四种不同催化剂下平均得率无显著差异 .3 试验某种钢的冲击值（kg ×m/cm2），影响该指标的因素有两个，一是含铜量A ，另试检验含铜量和试验温度是否会对钢的冲击值产生显著差异？（α=0.05） 解 根据问题，这是一个双因素无重复试验的问题，不考虑交互作用.设因素,A B 分别表示为含铜量和温度，试验指标为钢的冲击力，水平为12.假设样本观测值(1,2,3,1,2,3,4)ij y ij ==来源于正态总体2~(,),1,2,3,ij ij Y N i μσ=1,2,3,4j = .记i α⋅为对应于i A 的主效应；记j β⋅为对应于j B 的主效应；检验的问题：（1）10:i H α⋅全部等于零，11:i H α⋅不全等于零；（2）20:j H β⋅全部等于零，21:j H β⋅不全等于零； 计算结果：表5.3 双因素无重复试验的方差分析表查表0.95(2,6) 5.143F =，0.95(3,6) 4.757F =，显然计算值,A B F F 分别大于查表值，或p = 0.0005，0.0009 均显著小于0.05，所以拒绝1020,H H ，认为含铜量和试验温度都会对钢的冲击值产生显著影响作用.设每个工人在每台机器上的日产量都服从正态分布且方差相同 .试检验：（α=0.05）1）操作工之间的差异是否显著？ 2）机器之间的差异是否显著？3）它们的交互作用是否显著？解 根据问题，这是一个双因素等重复(3次)试验的问题，要考虑交互作用.设因素,A B 分别表示为机器和操作，试验指标为日产量，水平为12. 假设样本观测值(1,2,3,1,2,3,4)ijk y i j ==来源于正态总体2~(,),1,2,3,ij ij Y N i μσ= 1,2,3,4j =，1,2,3k = .记i α⋅为对应于i A 的主效应；记j β⋅为对应于j B 的主效应；记ij γ为对应于交互作用A B ⨯的主效应； 检验的问题：（1）10:i H α⋅全部等于零，11:i H α⋅不全等于零； （2）20:j H β⋅全部等于零，21:j H β⋅不全等于零； （3）30:ij H γ全部等于零，31:ij H γ不全等于零；计算结果：表5.4 双因素无重复试验的方差分析表查表0.95(3,24) 3.01F =，0.95(2,24) 3.4F =，0.95(6,24) 2.51F =，计算值 3.01,A F <3.4, 2.51B A B F F ⨯>>，或0.05A p >>，而,B A B p p ⨯均显著小于0.05，所以拒绝2030,H H ，接受10H ，认为操作工之间的差异显著，机器之间的差异不显著，它们之间的交互作用显著 . 5 某轴承厂为了提高轴承圈退火的质量，制定因素水平分级如下表所示因素 上升温度℃ 保温时间(h)出炉温度℃水平1 800 6 400 水平28208500试填好正交试验结果分析表并对试验结果进行直观分析和方差分析 .解 根据题意，这是一个3因素2水平的试验问题 .试验指标为硬度的合格率 .应选择正交表44(2)L 来安排试验，随机生成正交试验表如下：方差来源 自由度 平方和 均方 F 值 P 值 因素A 因素B 相互效应A ×B误差 总和3 2 6 24 352.750 27.167 73.5 41.333 144.750.917 13.583 12.250 1.7220.5323 7.8871 7.11290.6645 0.00233** 0.00192**由此可见第三号试验条件为：上升温度800℃、保温时间6h 、出炉温度500℃ . 直观分析需要计算K 值，计算结果如下：表5.6 计算表直观分析 由计算的K 值知，因素A 、B 、C 的极差分别为70，40，40，因此主次关系为A B C >=，B ，C 相当 .由于试验指标为硬度的合格率，应该是越大越好，所以各确定因素的水平分别是121,,A B C ，即最佳的水平组合是121A B C ，即最佳搭配为：上升温度800℃、保温时间8h 、出炉温度400℃.采用方差分析法，计算得下表：表5.7 方差分析表方差来源平方和 自由度均方差 F 值 A 1225 1 1225 1 B 400 1 400 0.33 C 400 1 400 0.33 误差 1225 1 1225 总和32504如果显著性检验水平取0.1α=，则查表得0.9(1,1)39.9F =，显然计算的F 值1,0.33A B C F F F ===均小于查表值，所以认为三个因素对结果影响都显著 .6问应选用哪张正交表安排试验，并写出第8号试验的条件；如果9组试验结果为（单位：kg/100m 2）：62.925，57.075，51.6，55.05，58.05，56.55，63.225，50.7，54.45，试对该正交试验结果进行直观分析和方差分析.解 该问题属于3因素3水平的试验问题，试验指标为水稻产量 .根据题意应选择正交表49(3)L 来安排试验，随机生成正交表如下：由表可知，第8号试验的条件：品种（A 3）珍珠矮11号，插值密度（B 2）3.75棵/100m 2 ，施肥量（C 1）0.75kg/100m 2纯氨； 直观分析需要计算K 值，计算结果如下：表5.9 计算表同上题进行直观分析，得出K 值的大小关系为：111312212223333132,,K K K K K K K K K >>>>>>由直观分析看出：本例较好的水平搭配是：113A B C 采用方差分析法，计算得下表：表5.10 方差分析表方差来源平方和自由度 均方差F 值A 1.759 2 0.879 0.0223B 65.861 2 32.931 0.8361C 6.660 2 3.330 0.0845 误差78.776 239.388 39.3880.9(2,2)9F =，所以认为三个因素对结果影响都不显著.7 在阿魏酸的合成工艺考察中，为了提高产量，选取了原料配比A ，吡啶量B 和反应时间C 三个因素，它们各取了7个水平如下：原料配比A ：1.0，1.4，1.8，2.2，2.6，3.0，3.4 吡啶量B ：10，13，16，19，22，25，28 反应时间C ：0.5，1.0，1.5，2.0，2.5，3.0，3.5试选用合适的均匀设计表安排试验，并写出第7号试验的条件；如果7组试验的结果（收率）为：0.33，0.336，0.294，0.476，0.209，0.451，0.482，试对该均匀试验结果进行直观分析并通过回归分析发现可能更好的工艺条件.解 根据题意选择均匀设计表47(7)U 来安排试验，有3个因素，根据使用表，实验安排如：表5.11 试验安排表所以第7号实验的条件为：原配料比3.4，吡啶量28ml，反应时间3.5h.通过直观分析，最好的实验条件是：原配料比3.4，吡啶量28ml，反应时间3.5h.通过回归分析，最合适的实验条件是：原配料比2.6，吡啶量16ml，反应时间0.5h.习题六1 从某中学高二女生中随机选取8名，测得其升高、体重如下：在绝对距离下，试用最短距离法和离差平方和法对其进行聚类分析.解由R软件，用最短距离（左）和差离平方和法（右）对题目进行聚类分析如下图6.1，表6.1和表6.2：最短距离法离差平方和法图6.1 聚类树形图表6.1 聚类附表(最短距离法)表6.2 聚类附表(离差平方和法)2 已知五个变量的距离矩阵为03674012340444401592343331).;2);3)036034022020401000⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭试用最短距离法和最长距离法对这些变量进行聚类，并画出聚类图和二分树.解 针对距离矩阵1），采用两种方法计算如下. ①最短距离法的聚类步骤如下：12345036740159036020w w w w w ⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪⎝⎭a ）将()236,1w w f h =合并为一类，，{}11456,,,,H w w w h =距离矩阵如下0743023060⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭{}()457457),,,2b w w h w w f h ==合并为一类，{}2167,,,H w h h =距离矩阵如下：034030⎛⎫ ⎪⎪ ⎪⎝⎭{}()()1681689),,3,3c w h h w h f h f h ===合并为一类，最后，，聚类图和树状图如图6.2：图6.2 聚类图（左）与树状图（右）②最长距离法与最短距离法类似，步骤如下： a ）()236,1w w f h =合并为一类，{}11456,,,,H w w w h =距离矩阵如下0746025090⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭ {}(){}4574572167),,,2,,,b w w h w w f h H w h h ===合并为一类，距离矩阵如下：067090⎛⎫⎪⎪ ⎪⎝⎭{}()()1681689),,69c w h h w h f h f h ===合并为一类，最后，，，聚类图和树状图如图6.3：图6.3 聚类图（左）与树状图（右）（2）针对距离矩阵2）012340234034040⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪⎝⎭①最短距离法的聚类步骤如下 a ）()216,1w w f h =合并为一类，{}13456,,,,0342043040H w w w h =⎛⎫⎪⎪ ⎪ ⎪⎝⎭距离矩阵如下{}()367367),,,2b w h h w h f h ==合并为一类，{}24567,,,,H w w h h =聚类矩阵如下：043040⎛⎫⎪⎪ ⎪⎝⎭{}(){}()4784789879),,3,,4c w h h w h f h h w h f h ====合并为一类，最后，，聚类图和树状图如图6.4：图6.4 聚类图（左）与树状图（右）②由于本题数据的特殊性，最长距离法与最短距离法结果相同（略）. (3)044440333022010⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪⎝⎭最短距离法的聚类步骤如下a ) ()456,1w w f h =合并为一类，{}11236,,,,H w w w h =距离矩阵如下0444033020⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭{}(){}36736724567),,,2,,,,b w h h w h f h H w w h h ===合并为一类，距离矩阵如下：044030⎛⎫⎪⎪ ⎪⎝⎭{}(){}()4784789879),,3,,4c w h h w h f h h w h f h ====合并为一类，最后，，，聚类图和树状图如图6.5：图6.5 聚类图（左）与树状图（右）由于本题数据的特殊性，最长距离法与最短距离法结果相同(略).3 在一项关于作物对土壤营养的反应的研究中，要测定土壤的总磷量和总氮量（占干物质重的百分比），今对10份土样测得数据如下：在绝对距离下，试用重心法对其进行聚类分析.解由R软件得到重心法聚类分析的结果如图6.6与表6.3：图6.6 聚类树形图表6.3 聚类过程记录表4 1975年Dagnelie收集了11年的气象数据资料如下表其中：x 1—前一年11月12日的降水量；x 2—7月均温；x 3—7月降雨量；x 4—月日辐射，试对这四个气象因子进行主成分分析. 解 由R 软件分析得到如下表6.4，6.5：表6.4 各主成分的重要性:主成分1 主成分2 主成分3 主成分4 标准差 1.6103349 0.9890848 0.53407741 0.37854199 方差贡献率 0.6482947 0.2445722 0.07130967 0.03582351 累积贡献率0.64829470.89286680.964176491.00000000表6.5 因子荷载:主成分1 主成分2 主成分3 主成分4 X1 0.291 0.871 0.332 -0.214 X2 -0.506 0.425 -0.742 -0.111 X3 0.577 0.136 -0.418 0.688 X4-0.5710.2050.4040.685由于前两个主成分对应的累积贡献率已经达到89.287，因此选取主成分的数目为2.5 对某初中12岁的女生进行体检，测量其身高x 1、体重x 2、胸围x 3和坐高x 4，共测得58个样本，并算得1234(,,,)x x x x x ='的样本协方差为19.9410.5023.566.5919.7120.958.637.97 3.937.55S ⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭ 试进行样本主成分分析.解 首先计算样本的相关系数矩阵：10.484410.32240.887210.70330.59760.31251⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭设相关系数矩阵的特征值和特征向量分别为d 和v 阵，计算得到0.0546000 0 0.312600= 000.96470 000 2.6681d ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭即四个特征值依次为：2.6681，0.9647，0.3126，0.0546，前两个主成分的累计贡献率为：90.8471%，因此提取主成分为2.四个特征根相应的特征向量为0.06000.70600.5333 0.4620 0.7317 0.17430.34040.5642=0.60570.19320.60400.48060.30690.65870.48460.4870v -⎛⎫ ⎪-⎪ ⎪--- ⎪-⎝⎭ 因此，两个主成分的表达式为：112340.060.73170.60570.3069z x x x x =+-- 212340.7060.17430.19320.6587z x x x x =-+-+6 比较因子分析和主成分分析模型的异同，阐明两者的关系. 解（1）提取公因子的方法主要有主成分法和公因子法.若采取主成分法，则主成分分析和因子分析基本等价，该法从解释变量的变异的角度出发，尽量使变量的方差能被主成分解释；而公因子法主要从解释变量的相关性角度，尽量使变量的相关程度能被公因子解释，当因子分析目的重在确定结构时则用到该法.（2）主成分分析和因子分析都是在多个原始变量中通过他们之间的内部相关性来获得新的变量，达到既减少分析指标个数，又能概括原始指标主要信息的目的.但他们各有其特点：主成分分析是将n 个原始变量提取m 个支配原始变量的公因子，和1个特殊因子，各因子之间可以相关或不相关.（3）统用降维的方法，但差异也很明显：主成分分析把方差划分为不同的正交成分，而因子分析则把方差化分为不同的起因因子；因子分析中的特征值的计算只能从相关系数矩阵出发，且必须把主成分划分为因子.（4）因子分析提取的公因子比主成分分析提取的主成分更具有可解释性.（5）两者分析的实质及重点不同.主成分的数学模型为Y AX =，因子分析的数学模型为X AF ε=+.因而可知主成分分析是实际上是线性变换，无假设检验，而因子分析是统计模型，某些因子模型是可以得到假设检验的；主成分分析主要综合原始数据的信息，而因子分析重在解释原始变量之间的关系.（6）SPSS 数据的实现：两者都通过“analyze data reduction Factor···”过程实现，但主成分分析主要使用“descriptires ”,“extraction ”,“stores ”对话框，而因子分析处使用这些外，还可使用“rotaction ”对话框进行因子旋转.7 试对第4题的变量作因子分析，并将结果和上面的结果进行比较. 解 用SPSS 分析，计算结果如下表6.6-6.8：表6.6 反应压缩比情况表 提取方法: 主成分法计算的相关系数矩阵的特征值和方差贡献率：表6.7 方差解释度提取方法: 主成分法表6.8 主成分矩阵8 为研究某一树种的叶片形态，选取50片叶测量其长度x 1（mm ）和宽度x 2（mm ），按样本数据求得其平均值和协方差矩阵为：129048134,92,4845x x S ⎛⎫=== ⎪⎝⎭求出相关系数阵R ，并由R 出发作因子分析；解1）求相关系数矩阵：904810.7303,48900.73031S R ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭ 2）用R 软件求R 的特征根及其相应的特征向量，软件输出结果如下：$values[1] 2.99393809 0.07273809 $vectors[,1] [,2] [1,] 0.7071068 -0.7071068 [2,] 0.7071068 0.7071068122.9939,0.0727,λλ∴==12(),()0.7071,0.7071-0.7071,0.7071T Tηη==3) 求载荷矩阵A ：1.22350.19071.22350.1907A -⎛⎫= ⎪⎝⎭4）22121.5333, 1.5333,h h == 0.98810.154*0.98810.154A -⎛⎫= ⎪⎝⎭12121,1,0.3043,0.3043u u v v ===-=，222222000011112,0,()0.9074,20i i iii i i i i i A u B v C u v D u v =========-===∑∑∑∑9 1981年，生物学家Grogan 和Wirth 对两种蠓虫Af 和Apf 根据其触角长度x 1和翼长x 2进行了分类，分类的数据资料如下：Af 1 2 3 4 5 6 7 8 x 1 1.24 1.36 1.38 1.38 1.38 1.40 1.48 1.54 x 2 1.27 1.74 1.64 1.82 1.90 1.70 1.82 1.82 Apf 1 2 3 4 5 6 x 1 1.14 1.18 1.20 1.26 1.28 1.30 x 2 1.78 1.96 1.86 2.00 2.00 1.96 （1）试建立Af 和Apf 的Fisher 判别模型；（2）对样本（1.24，1.80），（1.28，1.84），（1.40，2.04）进行判别分类. 解 （1）建立Fisher 判别模型991122121111(,)(1.42,1.75),(,)(1.23,1.93)99T TT T i i i i i i x x y y μμ======∑∑120.08480.1490.01980.0218,0.1490.39120.02180.039A A ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭12120.0080.0130.0130.0332A A n n ⎛⎫+== ⎪+-⎝⎭∑()120.19,0.18Tμμ-=-，()()121 1.325,1.842T μμ+= 1345.05135.42135.4283.33--⎛⎫= ⎪-⎝⎭∑， 带入Fisher 判别函数 ()12345.05135.42[(,)(1.325,1.84)]0.19,0.18135.4283.33Tx x -⎛⎫-- ⎪-⎝⎭1291.301741.336944.534x x =--（2）把三个样本（1.24，1.80），（1.28，1.84）,(1.4,2.04)带入模型，得到结果：三个样本均属于Apf 类.10 在两个玉米品种之间进行判别：137玉米G 1和甜玉米G 2，选取的两个变量是：x 1—玉米果穗长；x 2—玉米果穗直径，两个类的样本容量为n 1＝n 2＝40，实际算得两个类的样本均值和样本协方差为：121218.5625.348.120 4.4589.661 3.720,,,5.98 4.12 4.458 4.350 3.720 3.410x x S S ⎛⎫⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭试建立G 1，G 2的Bayes 类线性判别函数.解 因为已知两类的样本均值和样本协方差为：12(18.56,5.98),(25.34,4.12)T T x x ==，128.120 4.4589.661 3.720,4.458 4.350 3.720 3.410S S ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭可计算得到修正的公共协方差矩阵和逆矩阵12120.2280.1450.1450.0992A A n n ⎛⎫+== ⎪+-⎝⎭∑，15.6393.738.25147.38--⎛⎫= ⎪-⎝⎭∑()()()121216.78,1.86,21.95,5.052TTμμμμ-=-+= 带入Fisher 判别函数()112121(())()2T W x x μμμμ-=-+-∑ ()()12 5.6393.73[(,)21.95,5.05] 6.78,1.868.25147.38Tx x -⎛⎫=-- ⎪-⎝⎭1274.396.951141.29x x =-+-。
清华大学高等数值分析试卷(汇编)
（一）对任意的 矩阵，都能用左乘和右乘（不一定相同的）初等反射阵（Householder阵）将其变为以下结构的矩阵吗？
(a)
(b)dip vt.浸；蘸 (b) (c)
△masterpiece n.杰作；名著其中 表示元素可以非0。对(a), (b), (c)形矩阵分别回答。
in search of寻找（提示：考虑方程组 ， ）
(c) ，且 。
（三）
（四）bathtub n.浴缸；澡盆写出与下述微分方程边值问题等价的Galerkin变分问题，
这里 已给定。
第2页/共2页
清华大学研究生“高等数值分析”试题（2012.1.10）
姓名学号所在系
填空：（28分）
（一）设矩阵 ，则 ， 。
（二） 设 ，请给出一个 的奇异值分解 ，
其中 ， ， 。
对上面的 ，若 ，使 ，则 ，这里 。பைடு நூலகம்
（三）设 对称正定，用CG法求解 ，若第一、二步迭代搜索方向分别为 、 ，则2步后余量 沿方向（不计正负）___________。
第1页/共2页
△hike vi. & n.远足；徒步旅行
（二）
（三）possess vt.拥有；具有；支配若用GMRES法解方程组 ， 非奇异， ，取 作为初值， ，从 开始Arnoldi过程，则必有 吗？为什么？这里 ， 为GMRES法第k步所得近似解， 。
（四）
（五）△nationalism n.民族主义；设用不动点迭代法 解非线性方程组， 为 的解，迭代函数 在 处Frechet可导且 矩阵，问此时迭代法是否局部超线性收敛？为什么？
textbook n.教科书；课本
数学分析中的典型问题和方法第一章课后习题答案裴礼文
裴礼文第一章习题解答1.1.1 求复合函数表达式:(1) 已知,,求;(南京邮电大学等)(2) 设,试证明,并求(华中理工大学)1.1.2 是否存在这样的函数,它在区间上每点取有限值,在此区间的任何点的任意邻域内无界. (上海师范大学)1.1.3 试说明能有无穷多个函数,其中每个函数皆使为上的恒等函数.1.1.4 设为上的奇函数,,,.1)试用表达和;2)为何值时,是以为周期的周期函数. (清华大学)1.1.5 设(即的小数部分),,说明这时为何不是周期函数.类似地也如此.从而周期函数的和与差未必是周期函数.1.1.6设是上的实函数, 的图像以直线和直线分别作为其对称轴, 试证必是周期函数, 且周期为.1.1.7 设是上的奇函数, 并且以直线作为对称轴,试证必为周期函数并求其周期.1.1.8 设是上以为周期的周期函数, 且在上严格单调, 试证不可能是周期函数1.1.9 证明确界的关系式:1) 叙述数集的上确界定义, 并证明: 对于任意有界数列,总有(北京科技大学)2) 设是两个由非负数组成的任意数集, 试证1.1.10 试证:若,则必达到下确界(即使得). (武汉大学)1.1.11 设是上的实函数, 且在上不恒等于零，但有界，试证:、1.1.12 设是闭区间上的增函数，如果,试证，使得(山东大学)1.1.13 设在, 试证，使得. (福建师范大学)1.2.11) 已知, 求证:(武汉大学, 哈尔滨工业大学)2) 用语言证明(清华大学)1.2.2 用方法证明:1)2)3)1.2.3 设, 试用方法证明：若, 则1.2.4 设,试证收敛.1.2.5 为一数列.试证: 若(为有限数)则(首都师范大学)1.2.6 设且时有.已知中存在子序列.试证(武汉大学)1.2.7 设, 求证发散.1.2.8 判断题:设是一个数列, 若在任一子序列中均存在收敛子列则必为收敛数列. (北京大学)1.2.9 设为单调递增数列，为其一子列，若,试证(华中师范大学)1.2.10 设是一个无界数列,但非无穷大量,证明: 存在两个子列，一个是无穷大量，另一个是收敛子列. (哈尔滨工业大学)1.2.11 设函数在0的某个邻域有定义，;且当时，, ,时,对于一切, 有;另设.试证当右端极限存在时成立1.2.12 证明.并求1.3.1 求极限(北京航空航天大学,中国科技大学)1.3.2 证明公式:1.3.3 求1.3.4 求1.3.51.3.6 求(华中师范大学)1.3.7 求(湖北大学)1.3.8 设在上连续,求1.3.9 设极限存在,试求1)2)1.3.10 设,求(陕西师范大学)1.3.11 求.(内蒙古大学)1.3.12 .(中国科学院)1.3.13 计算(中国科学院)1.3.14 若求.(上海工业大学)1.3.15 求华中师范大学)1.3.16 证明: 当时,1.3.17 求(浙江大学)1.3.18 ,求(国防科技大学)1.3.19 求(华中师范大学)1.3.20 求(武汉大学)1.3.21 设是上的可微函数,,试证1.3.22 设是上的可微函数,,试证1.3.23 ,试证:1)2) (南开大学)1.3.24 对, ,,令试先证明:然后求解1.4.1 求,其中1) 设2) 设1.4.2 求(华中师范大学)1.4.3 已知数列满足条件证明:(四川大学, 国防科技大学)1.4.4 设.1) 若为有限数, 证明2) 若为, 证明: (南京大学)1.4.5 证明:若数列收敛于,且,,则(东北师范大学)1.4.6 已知存在,为单调增加的正数列,且,求证:(北京师范大学)1.4.7 若且,试证:1.4.8 求极限1)2)1.5.1 已知试证:存在并求其值.(中国科技大学,北京大学,哈尔滨工业大学,北京邮电大学等)1.5.2 设,证明:收敛,并求.(哈尔滨工业大学,华中理工大学等)1.5.3 设,证明:收敛并求其极限.(武汉大学,华中师范大学)1.5.4 设证明收敛并求其极限(华东师范大学)1.5.5 设,试证收敛,并求其极限.(华中理工大学,厦门大学,工程兵学院)1.5.6 求证:1.5.7 证明:1)存在唯一的使得;2)任给定则有(中国人民大学)1.5.8 证明数列.收敛.(北京师范大学)1.5.9 设,求. (武汉大学)1.5.10 设,数列由如下递推公式定义:求(浙江大学)1.5.11 设如果数列收敛,计算其极限,并证明数列收敛于上述极限.（武汉大学）1.5.12 设,其中:,试证:存在且为克普勒方程的唯一根.1.5.13 设(),试证:收敛.1.5.14 设是二正数,令.试证:和均收敛且极限相等. (大连理工大学)1.5.15 设和是任意两个整数,并且,还设求证: 和均收敛且极限相等.(中国科学院,安徽大学）1.5.16 讨论由所定义的数列的收敛性(南京大学)1.5.17 设中数列满足其中,证明:当有界时,有界. (清华大学)1.5.18 设,求极限.1.5.19 则1)(中国科学院)1.5.20 设连续函数在上是正的,单调递减的,且.证明:数列收敛(清华大学)1.5.21 已知证明:及存在且相等,并求出该极限. (内蒙古大学)1.5.22证明:数列的极限存在,并求其极限. (国外赛题)1.5.23 设是如此数列:证明收敛并求其极限. (国外赛题)1.5.24 设,求1.5.25 设证明1.5.26 设试计算:(国外赛题)1.5.27 收敛,数列()由下式确定:证明是递增的收敛数列(福建师范大学)1.6与1.7 习题机动跳过1.8.1 设函数在有限区间上有定义,满足,存在的某个开邻域,使得在上有界.(1).证明:当时,在上有界;(2).当时,在上一定有界吗? (厦门大学)1.8.2 设在上有定义且在每一点处函数的极限存在,求证:在上有界. (哈尔滨工业大学)1.8.3 设在内有定义,当时,有1.8.4 用有限覆盖定理证明:任何有界数列必有收敛子列.(西北大学)1.8.5 试用区间套定理重新证明练习1.1.13:“上,”(福建师范大学)。
清华大学数值分析A往年试题回顾
5 道大题，若干小题，卷面成绩满分70
1.(1)求f(x)=sqrt(1-x A2)在span{1,x,xA2}上，权函数为rou=1/sqrt(1-x A2)的最佳平方逼近多项式
⑵求证高斯型求积公式中的A(k)满足A(k)= / p(x)l(x)dx= / p(x)lA其(X)dXk)为Lagrange多项
式
2.(1)Ax=b中A非奇异，则用J法、GS法、SOR法、SSOR法求解等价方程ATAx=ATb各种方法的收敛性怎样？(其中0<w<2)
(2)A严格对角占优，求证其有唯一的LU分解，对称矩阵[3 1 0;1 3 1;0 1 3]求其cholysky分解
3.(1)写出用Lanczos方法计算某矩阵第一列的a和B
⑵已知矩阵[3 0 0;0 3 2;0 2 3]，求其QR分解，计算一步H'=RQ
4(1)f(x)=[x2A2-x1A2-x1 其精确解为x*=[0 0 0],写出牛顿法的计算公式sin(x1A2)-x2];
(2)已知G(x)=[x2A2-x1A2 sin(x1A2)];
给出区域D 使得在此区域内的初始值可以收敛到精确解，并说明原因
5.(1)线性2 步法-0.5y(n)-0.5y(n+1)+y(n+2)=h/2*(f(n)+f(n+1)+f(n+2))，计算其局部阶段误差的阶数若h=0.1,判断其稳定性
⑵已知R(z)的稳定函数是exp(z)的pade(1,2)逼近多项式，计算其稳定域，是否是A-稳定？(pade 逼近的计算公式卷子上给了)。
清华电气高数真题答案解析
清华电气高数真题答案解析清华大学电气工程系的高等数学课程一直以难度较高而著名，相应的，其真题也备受关注。
本文将对清华电气高数真题的答案进行解析，以帮助读者更好地理解和掌握高数知识。
一、选择题解析选择题是考察学生对基础知识的掌握和理解程度的重要方式。
下面解析一道典型的选择题：1. 设函数 f(x) = x^3 - 3x^2 + 2x + 1，下列命题不正确的是：A. f(x) 在 (-∞, +∞) 上为增函数B. f(x) 在 [-1, 1] 上有唯一的极值点C. f'(x) 在 (0, 1) 上存在驻点D. f''(x) 在 (-∞, ∞) 上存在零点首先我们对 f(x) 进行一阶和二阶求导，得到 f'(x) = 3x^2 - 6x + 2 和 f''(x) = 6x - 6。
A 选项是正确的，因为 f'(x) = 3x^2 - 6x + 2 为二次函数，其系数 3 > 0，所以在整个实数区间上 f(x) 为增函数。
B 选项是正确的，因为 f'(x) 的二次函数图像是一个开口朝上的抛物线，因此在 [-1, 1] 上一定有极值点。
C 选项是不正确的，因为 f'(x) 为一个二次函数，其图像没有驻点。
D 选项是正确的，因为 f''(x) = 6x - 6 为一次函数，根据一次函数的性质，其在整个实数区间上一定存在零点。
综上所述，选择题的正确答案为 C。
通过解析这道题目，我们可以看出对函数的求导和图像分析是解答选择题的关键。
二、计算题解析计算题是考察学生对基础计算和运用所学知识解决实际问题的能力的重要内容。
下面解析一道典型的计算题：2. 计算极限lim(x→0) (tan(3x) - 3sin(x)) / x^3。
我们可以用泰勒展开将 tan(3x) 和 sin(x) 在 x = 0 处展开，得到：tan(3x) = 3x + 9x^3 / 2 + O(x^5)sin(x) = x - x^3 / 6 + O(x^5)代入原式，并将高于 x^3 的项忽略，得到：lim(x→0) (tan(3x) - 3sin(x)) / x^3 = lim(x→0) (3x +9x^3 / 2 - 3x + 3x^3 / 2) / x^3= lim(x→0) (6x^2 + 9x^3) / 2x^3 = lim(x→0) (6 + 9x) / 2 = 6 / 2 = 3所以，极限的值为 3。
清华大学考研-清华大学考研数学 近五年线代真题考点分析
龙驭球、包世华 注册咨询工程师考试 教材编写委员会 翻译本 胡忠鲠 傅献彩 顾夏声等 周德庆 王家玲等 郭怀城等 马中 程声通 曾思育
王昆林 朱张校主编 秦曾煌主编 申永胜 吴宗泽 郁道银、谈恒英
王向荣
[英]杰弗瑞·杰里柯//苏 珊杰·里柯 译者：刘滨 谊
周维权
刘敦祯 潘谷西 陈志华 罗小未 张筑生 周民强，方企勤
张三慧
宋天佑，程鹏，王杏乔
邢其毅主编
薛华等 刘密新等
潘祖仁主编
何曼君等
606 生物学
《基础生命科学》 高等教育出版社 第二版
吴庆余
607 西方哲学史 《西方哲学简史》 北京大学出版社 2002
《外国城市建设史》 中国建筑工业出版社
《中国古代建筑史》 中国建筑工业出版社
《中国建筑史》
中国建筑工业出版社
《外国建筑史》
中国建筑工业出版社
《外国近现代建筑史》中国建筑工业出版社
601 艺术概论
《艺术概论》
文化艺术出版社
《美学概论》
人民出版社
《中国城市建设史》 中国建筑工业出版社
《外国城市建设史》 中国建筑工业出版社
郑君里等
《电磁场理论》 829 电磁场理论
清华大学出版社 2001 年 2003 年重 王蔷 李国定 龚克
印
《电动力学》
高教出版社 1997 年 第二版
郭硕鸿
《Introduction to Semiconductor Devices》
清华大学出版社
Donald A. Neamen