第七次 复数项级数、幂级数
幂级数经典课件

收敛域的性 质:收敛域 是一个开区 间且包含原 点
收敛域的应 用:在函数 分析、微积 分等领域有 广泛应用
幂级数的收敛域的性质
收敛半径:幂级 数在收敛域内收 敛
收敛域:幂级数 在收敛域内收敛 且收敛半径为R
收敛半径的性质: 收敛半径R是幂级 数收敛域的半径
收敛域的性质:收 敛域是幂级数收敛 的区间且收敛半径 为R
幂级数的性质
收敛性:幂级数 是否收敛取决于 其收敛半径
解析性:幂级数 在其收敛半径内 解析
幂级数的和:幂级 数的和等于其收敛 半径内的解析函数
幂级数的展开:幂 级数可以展开为泰 勒级数或其他幂级 数形式
幂级数的收敛性
收敛性定义:幂级数在收敛区间内其部分和数列的极限存在 收敛性判别:使用比值判别法、根判别法、积分判别法等 收敛性应用:在函数逼近、数值分析、微分方程求解等领域有广泛应用 收敛性研究:幂级数的收敛性是数学分析中的重要课题有许多研究成果和理论
幂级数的求和的定义与性质
幂级数的求和: 将无穷多个幂 级数项相加得 到新的幂级数
求和的定义: 求和是指将无 穷多个幂级数 项相加得到新
的幂级数
求和的性质: 求和后的幂级 数具有与原幂 级数相同的收 敛半径和收敛
域
求和的应用: 求和在解决数 学问题、物理 问题等方面有
广泛应用
幂级数的求积的定义与性质
幂级数在解决初等数学问题中的应用
幂级数在微积分中的应用
幂级数在函数逼近中的应 用
幂级数在数值分析中的应 用
幂级数在概率论中的应用
幂级数的展开式的定义
幂级数:由无穷多个项组成的函数 展开式:将幂级数表示为无穷多个项的和 展开式形式:_0 + _1x + _2x^2 + ... 展开式的应用:在数学、物理、工程等领域广泛应用
复数项级数与幂级数

那末级数 � 发散.
=1
说明: 与实数项级数相同, 判别复数项级数敛散
性的基本方法是: 利用极限 lim sn = s .
n→ ∞
8
3.复数项级数收敛的条件
∞
∞
(1)※定理2 级数 � = � ( + ) 收敛的
∞
证
=
=
∞
充要条件 � 和 � 都收敛.
n =1
19
级数最前面n项的和
sn ( z ) = f 1 ( z ) + f 2 ( z ) + + f n ( z )
称为这级数的部分和.
和函数
如果对于 D 内的某一点 z0 , 极限 lim sn ( z0 ) = s( z0 )
n→∞
∞
存在, 那末称级数 ∑ f n ( z ) 在 z0 收敛 , s( z0 )称为
=
称为复数项无穷级数.
部分和 其最前面 n 项的和
= + + ⋯ + 称为级数的部分和.
7
2. 收敛与发散
∞
如果部分和数列 { sn } 收敛 , 那末级数 � 收敛,
并且极限 lim sn = s 称为级数的和 .
n→ ∞
=1
如果部分和数列 { sn } 不收敛 ,
规定 ∞ = +∞
5
※例2 证明:
已知
lim =
→∞
, <
,
<
∞ , >
lim
∞,
> →∞ =
, =
,
=
不存在, = −
复变函数的级数

收敛,则当 z z0 z1 z0 时绝对收敛;
n
cn (z z0 )n cn (z1 z0 )n
z z0 z1 z0
n
M z z0 z1 z0
• z1 z0•
z•
因为
z z0 1, z1 z0
n
所以
M z z0 z1 z0
收敛。
cn (z z0 )n 收敛。
n0
cn (z z0 )n 绝对收敛。
n0
如果级数 cn (z z0 )n 在 z z2
n0
则当 z z0 z2 z0 时发散。
处发散,
• z3
利用反证法可以说明:
如 果 在 z3 收 敛 , 则 在 z2 收敛,矛盾。
z0• •z2
幂级数存在收敛半径 R
R
(1) R 0 时幂级数只在 z z0 点收敛
a
ba
b a
当 z a 1 即 z a ba 时
ba
1
zb
1 ba
n0
z b
a a
n
n0
(b
1 a)n1
(z
a)n
2. 幂级数的性质
定理3.9 级数 an zn 和 bn zn 的收
n0
n0
敛半径分别为 R1 和 R2 则在
z min{R1, R2}
内:
(1) an zn bn zn (an bn )zn
2
n
n0 n!
z 2n
n0 (2n)!
z
2 n 1
n0 (2n 1)!
都收敛
3.2 幂级数
1. 幂级数的概念
cn (z z0 )n c0 c1(z时
cn zn c0 c1z cn zn
幂级数ppt

定理 1 (Abel 定理)
(1)如果级数 an x n 在 x x0 ( x0 0)处收敛,则
n0
它在满足不等式 x x0 的一切 x处绝对收敛;
(2)如果级数 an x n 在 x x0处发散,则它在满
n0
足不等式 x x0 的一切 x处发散.
几何说明
收敛区域
o
• • •• • • ••• • •
发散区域 R
R 发散区域 x
推论
如果幂级数 an x n 不是仅在x 0 一点收敛,也
n0
不是在整个数轴上都收敛,则必有一个完全确定
的正数 R 存在,它具有下列性质: 当 x R时,幂级数绝对收敛; 当 x R时,幂级数发散; 当 x R与x R时,幂级数可能收敛也可能发散.
15
收敛半径为R 1 ,收敛区间为(1,2).
2
当x 2时,原级数化为收敛的 交错级数
(1)n
;
x 1时,原级数化为
1 ,发散.
n0 2n 1
n0 2n 1
因此原级数的收敛域为 (1,2 ].
三、幂级数的运算
1、代数运算性质
设 an xn和 bn xn的收敛半径各为R1和R2 ,
n0
n0
证明 对级数 an xn 应用达朗贝尔判别法
n0
lim
n
an1 an
x n1 xn
lim an1 n an
x
x,
17
(1)由比值审敛法, 当 | x | 1 时,
级数| an xn | 收敛, 从而级数 an xn绝对收敛.
n0
n0
当 | x | 1 时,
级数 | an xn | 发散,
n0
幂级数的知识点

幂级数是数学中非常重要的概念之一,它在许多领域都有广泛的应用,例如物理学、工程学和计算机科学等。
本文将通过逐步思考的方式介绍幂级数的基本概念、性质和应用。
1. 幂级数的定义幂级数是一种形式为∑(an⋅x^n)的级数,其中an是一系列常数,x是变量。
幂级数可以看作是多项式的无穷级数形式,每一项的系数an和变量的幂次n可能会随着n的增大而变化。
2. 幂级数的收敛性为了讨论幂级数的性质和应用,我们首先需要了解收敛性的概念。
对于给定的幂级数,如果存在一个实数r,使得当|x| < r时级数收敛,而当|x| > r时级数发散,那么我们称r为幂级数的收敛半径。
收敛半径是幂级数的一个重要性质,决定了级数的收敛范围。
3. 幂级数的求和幂级数的求和是一个重要的问题。
对于给定的幂级数,我们可以使用不同的方法来计算它的和,例如直接求和、利用级数的性质进行变换和利用数值计算方法等。
其中,直接求和方法常用于某些特殊的幂级数,而其他方法则更多地用于一般情况下的求和问题。
4. 幂级数的性质幂级数具有许多重要的性质,这些性质对于理解幂级数的行为和应用非常有帮助。
其中一些重要的性质包括线性性质、微分性质和积分性质。
这些性质可以简化对幂级数的操作和计算,使得我们能够更加灵活地应用幂级数解决问题。
5. 幂级数的应用幂级数在数学和其他领域中有广泛的应用。
其中一些应用包括: - 在数学分析中,幂级数可以用于表示和逼近函数。
- 在物理学中,幂级数可以用于描述物体的运动和力学性质。
- 在工程学中,幂级数可以用于建模和解决差分方程和微分方程。
- 在计算机科学中,幂级数可以用于设计算法和优化问题求解过程。
6. 幂级数的扩展除了普通的幂级数之外,还有其他一些相关的概念和扩展形式。
例如,幂级数可以推广为形式为∑(an⋅(x-c)^n)的幂级数,其中c是常数。
这种形式的幂级数称为幂级数的泰勒级数形式,它在函数逼近和微积分等领域有广泛的应用。
复数项级数
注意
n 的各项都是非负的实数,
n1
应用正项级数的审敛法则判定.
证
由于 n
an2 bn2 ,
n1
n1
而 an an2 bn2 , bn an2 bn2 ,
4.1 复数项级数
6
内容要点 1:复数项级数; 2:幂级数,阿贝尔定理,收敛圆和收敛半径,和函数 的性质;
3:解析函数的泰勒展式,一些初等函数的泰勒展开式;
4:罗朗级数,解析函数的罗朗展开式;
7
一、复数列的极限 先回顾一下实数序列收敛的定义!
1.定义 设 {n } (n 1,2,) 为一复数列, 其中 n an ibn , 又设 a ib 为一确定的复数, 如果任意给定 0, 相应地都能找到一个正数
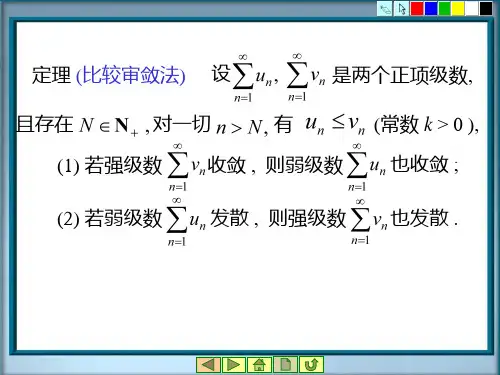
定理 (比较审敛法) 设
是两个正项级数,
且存在
对一切
有
(1) 若强级数 收敛 , 则弱级数
(常数 k > 0 ), 也收敛 ;
(2) 若弱级数 发散 , 则强级数 也发散 .
定理 . 比值审敛法 ( D’alembert 判别法)
设
为正项级数, 且 lim un1 , 则
n un
(1) 当 1 时, 级数收敛 ;
0
就能找到一个正数N, 当 n N 时,
(an ibn ) (a ib) ,
从而有 an a (an a) i(bn b) ,
所以
lim
n
an
a.
同理
lim
n
bn
b.
反之, 如果
lim
n
an
a,
lim
n
bn
b,
那末当n N 时,
an
a
第七次复数项级数、幂级数
第三章 级数
§3.1 复数项级数
1. 复数列的极限 2. 级数的概念 3. 级数收敛、绝对收敛、条件收敛
1. 复数列的极限
定义 设有复数列:{zn}, 其中zn=xn iyn ,
若存在复常数
a
ib,
使得
lim
n
xn
a,
lim
n
பைடு நூலகம்yn
b,
则称复数列zn收敛,并称复数 a ib为复数列zn
都有 Rn (z) sn (z) f (z) ,则称 un (z)在E n1
上一致收敛于f (z),简称一致收敛.
(2)性质:
性质(i) 若un (z)是连续函数列,且un (z)一致收敛于f (z), n1 则f (z)连续,并且有
l un (z)dz lun (z)dz.
n1
n1
性质(ii)(外尔斯特拉斯定理):
(1)
n1
1 n
发散,
n1
1 n2
收敛
,
n1
1 n
(1
i )发散. n
(2)
8i n
8n 收敛,
(8i )n 绝 对 收 敛 。
n0 n! n0 n!
n0 n!
(3)
n1
(
1)n
收
敛,
n
n1
1 2n
收敛
,
n1
(
(
1)n n
i 2n
)收敛.
又 (1)n 条件收敛,原级数非绝对收敛.
un(m) (z).
n1
证明: 见P81.
例2
证明复变函数项级数
k 1
sin k(k
常用幂级数展开
常用幂级数展开常用幂级数展开幂级数是一种数学工具,用于将一个函数表示为无限项的多项式的形式。
它在数学分析、物理学和工程学等领域中广泛应用。
在实际问题中,我们经常需要对复杂的函数进行近似计算,而幂级数展开提供了一种有效的方法来实现这一目标。
1. 幂级数的定义幂级数是指形如∑(n=0 to ∞)an(x-a)n的无穷级数,其中a和x是实数或复数。
其中,an称为系数,a称为展开点。
2. 幂级数收敛性幂级数的收敛性与展开点x-a之间的距离有关。
当x-a在某个区间内时,幂级数可能会收敛;当x-a超出该区间时,幂级数可能会发散。
3. 常见的幂级数展开公式以下是一些常见函数的幂级数展开公式:- 指数函数:e^x = ∑(n=0 to ∞)(x^n/n!)- 正弦函数:sin(x) = ∑(n=0 to ∞)((-1)^n*x^(2n+1)/(2n+1)!)- 余弦函数:cos(x) = ∑(n=0 to ∞)((-1)^n*x^(2n)/(2n)!)这些公式可以用于计算指数函数、正弦函数和余弦函数在某个展开点处的近似值。
4. 幂级数展开的应用幂级数展开在各个领域中有广泛的应用。
以下是一些常见的应用:- 物理学中的运动学问题:通过对位移、速度和加速度进行幂级数展开,可以得到近似解,从而简化运动学问题的分析。
- 工程学中的电路分析:通过对电流和电压进行幂级数展开,可以得到电路中各个元件的近似值,从而简化电路分析。
- 经济学中的财务分析:通过对收入和支出进行幂级数展开,可以得到财务指标的近似值,从而进行财务分析。
5. 幂级数展开的计算方法要计算一个函数的幂级数展开,通常有两种方法:- 直接计算法:根据函数的定义和性质,将其转化为一个已知函数或已知序列的形式,并利用已知序列的幂级数展开公式来计算。
- 微积分法:利用微积分中的导数和积分等运算规则,将函数表示为无穷项求和形式,并根据求导和积分公式逐项计算。
6. 幂级数展开的误差估计幂级数展开是一种近似方法,其结果与原函数之间存在误差。
幂级数概念
幂级数概念公司内部档案编码:[OPPTR-OPPT28-OPPTL98-§ 11. 3 幂级数一、函数项级数的概念函数项级数: 给定一个定义在区间I上的函数列{u n(x)}, 由这函数列构成的表达式u1(x)+u2(x)+u3(x)+ × × × +u n(x)+ × × ×称为定义在区间I上的(函数项)级数, 记为∑∞=1) (nnxu.收敛点与发散点:对于区间I内的一定点x0, 若常数项级数∑∞=1) (nnxu收敛, 则称点x0是级数∑∞=1) (nnxu的收敛点. 若常数项级数∑∞=1)(nnxu发散, 则称点x0是级数∑∞=1) (nnxu的发散点.收敛域与发散域:函数项级数∑∞=1) (nnxu的所有收敛点的全体称为它的收敛域, 所有发散点的全体称为它的发散域.和函数:在收敛域上, 函数项级数∑∞=1) (nnxu的和是x的函数s(x),s(x)称为函数项级数∑∞=1) (nnxu的和函数, 并写成∑∞==1)()(nnxuxs.∑u n(x)是∑∞=1) (nnxu的简便记法, 以下不再重述.在收敛域上, 函数项级数∑u n(x)的和是x的函数s(x),s (x )称为函数项级数∑u n (x )的和函数, 并写成s (x )=∑u n (x ).这函数的定义就是级数的收敛域, 部分和:函数项级数∑∞=1)(n n x u 的前n 项的部分和记作s n (x ),函数项级数∑u n (x )的前n 项的部分和记作s n (x ), 即 s n (x )= u 1(x )+u 2(x )+u 3(x )+ × × × +u n (x ). 在收敛域上有)()(lim x s x s n n =∞→或s n (x )?s (x )(n ??) .余项:函数项级数∑∞=1)(n n x u 的和函数s (x )与部分和s n (x )的差r n (x )=s (x )-s n (x )叫做函数项级数∑∞=1)(n n x u 的余项.函数项级数∑u n (x )的余项记为r n (x ), 它是和函数s (x )与部分和s n (x )的差 r n (x )=s (x )-s n (x ). 在收敛域上有0)(lim =∞→x r n n .二、幂级数及其收敛性 幂级数:函数项级数中简单而常见的一类级数就是各项都幂函数的函数 项级数, 这种形式的级数称为幂级数, 它的形式是a 0+a 1x +a 2x 2+ × × × +a n x n + × × × ,其中常数a 0, a 1, a 2, × × × , a n , × × ×叫做幂级数的系数. 幂级数的例子:1+x +x 2+x 3+ × × × +x n+ × × × , !1 !2112⋅⋅⋅++⋅⋅⋅+++n x n x x .注: 幂级数的一般形式是a 0+a 1(x -x 0)+a 2(x -x 0)2+ × × × +a n (x -x 0)n + × × × , 经变换t =x -x 0就得a 0+a 1t +a 2t 2+ × × × +a n t n + × × × . 幂级数1+x +x 2+x 3+ × × × +x n + × × ×可以看成是公比为x 的几何级数. 当|x |<1时它是收敛的; 当|x |?1时, 它是发散的. 因此它的收敛 域为(-1, 1), 在收敛域内有11132⋅⋅⋅++⋅⋅⋅++++=-n x x x x x.定理1 (阿贝尔定理) 如果级数∑∞=0n n n x a 当x =x 0 (x 010)时收敛, 则适合不等式|x |<|x 0|的一切x 使这幂级数绝对收敛. 反之, 如果级数∑∞=0n n n x a 当x =x 0时发散, 则适合不等式|x |?|x 0|的一切x 使这幂级数发散.定理1 (阿贝尔定理) 如果级数∑a n x n 当x =x 0 (x 010)时收敛, 则适合不等式|x |<|x 0|的一切x 使这幂级数绝对收敛. 反之, 如果级数∑a n x n当x =x 0时发散, 则适合不等式|x |?|x 0|的一切x 使这幂级数发散.提示: ∑a n x n是∑∞=0n n n x a 的简记形式.证 先设x 0是幂级数∑∞=0n nn x a 的收敛点, 即级数∑∞=0n n n x a 收敛. 根据级数收敛的必要条件, 有0lim 0=∞→nn n x a , 于是存在一个常数M , 使 | a n x 0n |£M (n =0, 1, 2, × × ×). 这样级数∑∞=0n n n x a 的的一般项的绝对值n n n n n nn n nn x x M x x x a x x x a xa ||||||||||00000⋅≤⋅=⋅=. 因为当|x |<|x 0|时, 等比级数nn x x M ||00⋅∑∞=收敛, 所以级数∑∞=0||n n n x a 收敛, 也就是级数∑∞=0n n n x a 绝对收敛.简要证明 设∑a n x n 在点x 0收敛, 则有a n x 0n ?0(n ??) , 于是数列{a n x 0n }有界, 即存在一个常数M , 使| a n x 0n |£M (n =0, 1, 2, × × ×).因为 n n n n n nn n n n x x M x x x a x x x a x a || |||| || ||00000⋅≤⋅=⋅=,而当||||0x x <时, 等比级数n n x x M ||0⋅∑∞=收敛, 所以级数∑|a n x n|收敛, 也就是级数∑a n x n绝对收敛.定理的第二部分可用反证法证明. 倘若幂级数当x =x 0时发散而有一点x 1适合|x 1|>|x 0|使级数收敛, 则根据本定理的第一部分, 级数当x =x 0时应收敛, 这与所设矛盾. 定理得证.推论 如果级数∑∞=0n n n x a 不是仅在点x =0一点收敛, 也不是在整个数轴上都收敛, 则必有一个完全确定的正数R 存在, 使得 当|x |<R 时, 幂级数绝对收敛; 当|x |?R 时, 幂级数发散;当x =R 与x =-R 时, 幂级数可能收敛也可能发散.收敛半径与收敛区间: 正数R 通常叫做幂级数∑∞=0n n n x a 的收敛半径? 开区间(?R ? R )叫做幂级数∑∞=0n n n x a 的收敛区间? 再由幂级数在x ??R 处的收敛性就可以决定它的收敛域? 幂级数∑∞=0n n n x a 的收敛域是(-R , R )(或[-R , R )、(-R ,R ]、[-R , R ]之一.规定: 若幂级数∑∞=0n n n x a 只在x =0收敛, 则规定收敛半径R =0 , 若幂级数∑∞=0n n n x a 对一切x 都收敛, 则规定收敛半径R =+¥, 这时收敛域为(-¥, +¥).定理2如果ρ=+∞→||lim 1n n n a a , 其中a n 、a n +1是幂级数∑∞=0n n n x a 的相邻两项的系数, 则这幂级数的收敛半径⎪⎪⎩⎪⎪⎨⎧+∞=≠=∞+=ρρρρ 00 10R ?定理2如果幂级数∑∞=0n n n x a 系数满足ρ=+∞→||lim 1nn n a a , 则这幂级数的收敛半径 ⎪⎪⎩⎪⎪⎨⎧+∞=≠=∞+=ρρρρ 00 10 R ?定理2 如果ρ=+∞→||lim 1n n n a a , 则幂级数∑∞=0n n n x a 的收敛半径R 为? 当??0时ρ1=R ? 当??0时R ???? 当????时R ?0? 简要证明: || ||||lim ||lim 111x x a a x a x a n n n nn n n n ρ=⋅=+∞→++∞→. (1)如果0<r <+?, 则只当r |x |<1时幂级数收敛? 故ρ1=R .(2)如果r =0, 则幂级数总是收敛的, 故R =+?. (3)如果r =+?, 则只当x ?0时幂级数收敛, 故R =0.例1 求幂级数)1( 32)1(13211⋅⋅⋅+-+⋅⋅⋅-+-=--∞=-∑nx x x x n x n n n n n 的收敛半径与收敛域. 例1 求幂级数∑∞=--11)1(n n n nx 的收敛半径与收敛域.解 因为1111lim ||lim 1=+==∞→+∞→nn a an n n n ρ,所以收敛半径为11==ρR .当x =1时, 幂级数成为∑∞=--111)1(n n n, 是收敛的;当x =-1时, 幂级数成为∑∞=-1)1(n n, 是发散的. 因此, 收敛域为(-1, 1].例2 求幂级数∑∞=0!1n n x n!1 !31!21132⋅⋅⋅++⋅⋅⋅++++n x n x x x的收敛域.例2 求幂级数∑∞=0!1n n x n 的收敛域.解 因为0)!1(!lim !1)!1(1lim||lim 1=+=+==∞→∞→+∞→n n n n a a n n n n n ρ, 所以收敛半径为R =+¥, 从而收敛域为(-¥, +¥). 例3 求幂级数∑∞=0!n n x n 的收敛半径.解 因为+∞=+==∞→+∞→!)!1(lim ||lim 1n n a a n n n n ρ, 所以收敛半径为R =0, 即级数仅在x =0处收敛. 例4 求幂级数∑∞=022!)()!2(n nx n n 的收敛半径. 解 级数缺少奇次幂的项, 定理2不能应用. 可根据比值审敛法来求收敛半径:幂级数的一般项记为nn x n n x u 22)!()!2()(=. 因为 21||4 |)()(|lim x x u x u n n n =+∞→, 当4|x |2<1即21||<x 时级数收敛; 当4|x |2?1即21||>x 时级数发散, 所以收敛半径为21=R .提示? 2222)1(221)1()12)(22()!()!2(])!1[()]!1(2[)()(x n n n xn n xn n x u x u n n n n +++=++=++. 例5 求幂级数∑∞=-12)1(n n nnx 的收敛域.解 令t =x -1, 上述级数变为∑∞=12n n n nt . 因为 21)1(22 ||lim 11=+⋅⋅==++∞→n n a a n n n n n ρ, 所以收敛半径R =2.当t =2时, 级数成为∑∞=11n n , 此级数发散; 当t =-2时, 级数成为∑∞=-1)1(n n ,此级数收敛. 因此级数∑∞=12n n n nt 的收敛域为-2£t <2? 因为-2£x -1<2, 即-1£x <3, 所以原级数的收敛域为[-1, 3). 三、幂级数的运算设幂级数∑∞=0n nn x a 及∑∞=0n n n x b 分别在区间(-R , R )及(-R ¢, R ¢)内收敛, 则在(-R , R )与(-R ¢, R ¢)中较小的区间内有 加法: ∑∑∑∞=∞=∞=+=+000)(n n n n n n n n n n x b a x b x a , 减法: ∑∑∑∞=∞=∞=-=-0)(n n n n n n n n n n x b a x b x a ,设幂级数∑a n x n 及∑b n x n 分别在区间(-R , R )及(-R ¢, R ¢)内收敛, 则在(-R , R )与(-R ¢, R ¢)中较小的区间内有 加法: ∑a n x n +∑b n x n =∑(a n +b n )x n , 减法: ∑a n x n -∑b n x n =∑(a n -b n )x n .乘法: )()(0∑∑∞=∞=⋅n n n n n n x b x a =a 0b 0+(a 0b 1+a 1b 0)x +(a 0b 2+a 1b 1+a 2b 0)x 2+ × × ×+(a 0b n +a 1b n -1+ × × × +a n b 0)x n + × × ×性质1 幂级数∑∞=0n n n x a 的和函数s (x )在其收敛域I 上连续.如果幂级数在x =R (或x =-R )也收敛, 则和函数s (x )在(-R , R ](或[-R ,R ))连续.性质2 幂级数∑∞=0n n n x a 的和函数s (x )在其收敛域I 上可积? 并且有逐项积分公式∑∑⎰⎰∑⎰∞=+∞=∞=+===0100001)()(n n n n xn n x n n n xx n a dx x a dx x a dx x s (x ?I )? 逐项积分后所得到的幂级数和原级数有相同的收敛半径.性质3 幂级数∑∞=0n n n x a 的和函数s (x )在其收敛区间(?R ? R )内可导? 并且有逐项求导公式∑∑∑∞=-∞=∞=='='='110)()()(n n n n n n n n n x na x a x a x s (|x |?R )?逐项求导后所得到的幂级数和原级数有相同的收敛半径. 性质1 幂级数∑a n x n 的和函数s (x )在其收敛域I 上连续.性质2 幂级数∑a n x n 的和函数s (x )在其收敛域I 上可积? 并且有逐项积分公式∑∑⎰⎰∑⎰∞=+∞=∞=+===0100001)()(n n n n xn n x n n n xx n a dx x a dx x a dx x s (x ?I )? 逐项积分后所得到的幂级数和原级数有相同的收敛半径.性质3 幂级数∑a n x n 的和函数s (x )在其收敛区间(?R ? R )内可导? 并且有逐项求导公式∑∑∑∞=-∞=∞=='='='010)()()(n n n n n n n n n x na x a x a x s (|x |?R )?逐项求导后所得到的幂级数和原级数有相同的收敛半径.例6 求幂级数∑∞=+011n n x n 的和函数.解 求得幂级数的收敛域为[?1? 1)?设和函数为s (x ), 即∑∞=+=011)(n n x n x s ? x ?[?1? 1)? 显然s (0)=1.在∑∞=++=0111)(n n x n x xs 的两边求导得x x x n x xs n n n n -=='+='∑∑∞=∞=+11)11(])([001. 对上式从0到x 积分, 得)1ln(11)(0x dx xx xs x--=-=⎰.于是, 当x 10时, 有)1ln(1)(x x x s --=. 从而⎪⎩⎪⎨⎧=<<--=0 11||0 )1ln(1)(x x x x x s .因为⎰∑∑'+=+=∞=+∞=+x n n n n dx x n x n x xs 00101]11[11)( )1ln(11000x dx xdx x xx n n --=-==⎰⎰∑∞=,所以, 当x 10时, 有)1ln(1)(x xx s --=,从而 ⎪⎩⎪⎨⎧=<<--=0 1 1||0 )1ln(1)(x x x x x s .例6 求幂级数∑∞=+011n n x n 的和函数.解 求得幂级数的收敛域为[?1? 1)?设幂级数的和函数为s (x ), 即∑∞=+=011)(n n x n x s ? x ?[?1? 1)?显然S (0)?1? 因为⎰∑∑'+=+=∞=+∞=+x n n n n dx x n x n x xs 00101]11[11)( )11( )1ln(11000<<---=-==⎰⎰∑∞=x x dx xdx x xx n n ,所以, 当1||0<<x 时, 有)1ln(1)(x xx s --=?从而 ⎪⎩⎪⎨⎧=<<--=0 11||0 )1ln(1)(x x x x x s .由和函数在收敛域上的连续性? 2ln )(lim )1(1==-+-→x S S x ?综合起来得⎪⎩⎪⎨⎧=⋃-∈--=0 1)1 ,0()0 ,1[ )1ln(1)(x x x x x s .提示? 应用公式)0()()(0F x F dx x F x -='⎰? 即⎰'+=xdx x F F x F 0)()0()(?11132⋅⋅⋅++⋅⋅⋅++++=-n x x x x x .例7 求级数∑∞=+-01)1(n nn 的和.解 考虑幂级数∑∞=+011n n x n , 此级数在[-1, 1)上收敛, 设其和函数为s (x ), 则∑∞=+-=-01)1()1(n nn s .在例6中已得到xs (x )=ln(1-x ), 于是-s (-1)=ln2, 21ln )1(=-s , 即21ln 1)1(0=+-∑∞=n n n .。
数学幂级数知识点总结
数学幂级数知识点总结一、幂级数的基本概念1. 幂级数的定义幂级数是由形如$a_n z^n$($n$从0到$\infty$)的无穷多项式组成的级数。
其中$a_n$是级数的系数,$z$是自变量,$n$是正整数。
换句话说,级数的每一项都是$z$的幂函数。
2. 幂级数的收敛半径幂级数的收敛半径(又称为收敛域)是幂级数收敛到的最大半径,它可以通过求幂级数系数的极限来确定。
具体地说,如果极限 $\lim_{n \to \infty} \sqrt[n]{|a_n|}$ 存在,并且等于$R$,那么幂级数的收敛半径就是$R$。
收敛半径的值可以是0,也可以是正无穷大,也可以是一个实数。
3. 幂级数的收敛区间除了收敛半径外,幂级数还有一个收敛区间。
如果收敛半径是$R$,那么收敛区间就是令幂级数收敛的所有复数$z$的集合,这个集合可以是一个区间,也可以是一个线段,也可能是一个点。
4. 幂级数的性质幂级数有很多重要的性质,比如线性性质、微分和积分的性质、幂级数求导和求和的性质等,这些性质在分析和求解问题中非常有用。
二、幂级数的收敛性1. 幂级数的收敛域收敛域是指使幂级数收敛的所有自变量的集合。
根据幂级数的定义和收敛半径的概念,我们可以很容易地确定一个幂级数的收敛域。
2. 幂级数的收敛测试在实际应用中,我们常常需要判断一个幂级数是否收敛。
为了判断幂级数的收敛性,我们可以使用比较判别法、比值判别法、根值判别法、Raabe判别法等各种不同的方法。
3. 幂级数的绝对收敛性如果一个幂级数的每一项都是非负数,并且级数的收敛性不依赖于幂级数的项的排列顺序,那么这个幂级数就是绝对收敛的。
4. 幂级数的一致收敛性一致收敛是一种比较强的收敛性,它要求幂级数在其收敛域内的每一个点上都收敛,并且幂级数的收敛速度是一致的。
一致收敛的幂级数在求导、求和等操作中有着重要的应用。
三、幂级数的求和1. 幂级数的求和函数幂级数的和函数是指将收敛域内的每一个复数$z$代入幂级数中得到的函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若 zn 发散,而 zn收敛,则称 zn为条件收敛 .
n 1 n 1 n 1
i (1) n i 条件收敛。 例如: 2 绝对收敛, n n 1 n n 1
(5)绝对收敛级数的性质
性质1.
z
n 1
n
收敛 zn收敛,且 zn zn .
n
2. 复变函数项级数一致收敛概念与性质
(1)定义: 设E为函数项级数 un ( z )的收敛域,如果
n 1
0, N ( ) 0, 对每一个z E ,当n N ( )时, 都有 Rn ( z ) sn ( z ) f ( z ) ,则称 u n ( z )在E
2. 收敛定理
3. 收敛圆与收敛半径
4. 收敛半径的求法
1. 幂级数的概念
称复变函数项级数
n 2 n c ( z a ) c c ( z a ) c ( z a ) c ( z a ) n 0 1 2 n n 0
为幂级数,其中 cn与a均为复常数,点 a为幂级数的中心, cn为幂级数的系数。
( 2)
n 0
8i 8n ( 8i ) n 收敛, 绝对收敛。 n! n! n 0 n! n 0
n
(1)n 1 ( 1)n i (3) 收敛, 收敛, ( n )收敛. n n n 2 n 1 n 1 2 n 1
( 1)n 又 条件 收敛, 原 级 数 非 绝 对 收 敛 . n n 1
4. 收敛半径的求法
关于幂级数 cn ( z a) n 的收敛半径求法,有
n 0
1 / 比值法 若 lim cn1 , 则 R n c (阿贝尔) n 0
1 / 根值法 若 l i mn c , 则 R n n (柯西) 0
n 1
命题:
u ( z )收敛于f ( z)的充分必要条件是
n 1 n
0, N ( z, ) 0, 使当n N ( z , )时, Rn ( z ) ˆ f ( z ) sn ( z ) ,即 lim Rn ( z ) 0, z E.
n k 1
n
称f ( z )为 un ( z )的和函数。
若 un ( z )的和函数为f ( z ), 则称下列差值
n 1
n 1
Rn ( z ) ˆ f ( z ) sn ( z ) un1 ( z ) un 2 ( z ) 为级数 un ( z )的尾量。
n 1 n 1 n 1
证明 zn xn iyn
2 2 xn xn yn , 2 2 y n xn yn
n n
2 2 xn yn
由比较判定法
x 和 y 均绝对收敛,
n 1 n n 1 n
故 zn收敛。
n 1
zk zk , zn zn
⑵ 若幂级数 cn ( z a) n在z z0发散, 则对满足 z a z0 a
n 1
的z, 级数必发散. 证明: 见P82。
3. 收敛圆与收敛半径
由Able定理,幂级数的收敛范围不外乎下述 三种情况: (i)若对所有正实数都收敛,则幂级数在复平面上 处处收敛。
(ii )除z=a外,对所有的正实数都是发散的,这时,幂级 数在复平面上除z=a外处处发散。
(1)证明:当 z 1时,级数绝对收敛;
(2)证明:当 z 1时,级数发散;
(3)证明:对每一个 r : 0 r 1,级数在有界闭区域 Dr : z r
上一致收敛。
(4)证明:级数在有界区域 D: z 1内非一致收敛。
见P108题2
§3.3 幂级数
1. 幂级数的概念
(iii ) 0,使得 cn 收敛, 0,使得 cn n 发散.
n n 0 n 0
由Able 定理,在圆周 c :
小,在c外部都是蓝色, z a 内,幂级数收敛; 红、蓝色不会交错。故 一 定 cR: z - a R ,为红、 在圆周c : z a 外, 蓝两色的分界线。 幂级数发散.
sn ( z ) u1 ( z ) u2 ( z ) un ( z ) uk ( z )
k 1
n
称为复变函数项级数的部分和。
对于z0 D, 若 lim sn ( z0 ) s ( z0 ), 称级数(1) 在z0收敛,
n
其和为s ( z0 ), 并称z0为 u n ( z )的收敛点。
zn 收敛,并称复数 a ib为复数列zn 则称复数列
的极限,记作lim zn , 或 z n
zn 收敛于。 称复数列
例如
n
(n ), 此时也
n 2 复数列 zn in sin , (n 1,2,) 收敛, n 1 n
且 lim z n 1 2i.
收敛, 则称级数 zn收敛。 n 1 lim sn s称为级数的和 若部分和数列 {sn } n 不收敛,则称级数 zn发散
3i 3i 例如:复数项级数 n 收敛,其和为3i, 即有 n 3i. n 1 2 n 1 2
n 1
(2)复数项级数收敛的等价条件:
n n n
xn 和 yn 都收敛。
n 1
n 1
由定理1,复数项级数的收敛问题可归之为 两个实数项级数的收敛问题。
(3)级数收敛的必要条件
z 收敛
n 1 n
lim zn 0.
n
i cos 发散。 例如: n n 1
(4)定义
若 zn 收敛,则称 zn为绝对收敛;
n
2. 复数项级数的概念
(1)定义 设有复数列: {zn } {xn iyn },
称 zn z1 z2 zn 为复数项无穷级数 , 简称级数。
n 1
称级数的前n项和 sn z1 z2 zn zi 为级数的部分和。
i 1
n
其中cn a0bn a1bn 1 anb0 .
例1 下列级数是否收敛?是 否绝对收敛?
1 i (8i )n (1) (1 ) (2) n n 1 n n 0 n!
(1)n i (3) ( n) n 2 n 1
1 1 1 i 解 (1) 发 散 , 收敛, (1 )发 散. 2 n n 1 n n 1 n n 1 n
显然,< . 否则,幂级数将在处发散。 将收敛部分染成红色,发散 部分染成蓝色,逐渐变大, 在c内部都是红色,逐渐变
a
定义 这个红蓝两色的分界圆周cR叫做幂级数的 收敛圆;这个圆的半径R叫做幂级数的收敛半径。
(i) 幂级数在收敛圆内部收敛,在收敛圆外 部发散,在圆周上可能有收敛点,也可能有发 散点,具体问题要具体分析。 (ii) 幂级数的收敛范围是以a为中心,R为半径 的圆域。
若un ( z )在区域D内解析,在D上连续, un ( z )在D的
n 1
境界线l上一致收敛,则 ( 1 ) 函数F ( z )在D un ( z )在D内也收敛,并且它的和
n 1
内是解析的;
(m) ( 2 ) 由它们的m阶导数所组成的级数 u n ( z )在D内 n 1
§3.2 复变函数项级数 1. 复变函数项级数的概念 2. 一致收敛的概念与性质
1. 复变函数项级数的概念
定义 设有复变函数列: {un ( z)} z D,
称 un ( z ) u1 ( z ) u2 ( z ) un ( z ) (1)
n 1
为复变函数项级数。 复变函数项级数的前n项的和
也收敛,并且有 F ( m ) ( z ) u n ( z ) n 1
(m)
(m) un ( z ). n 1
证明: 见P81.
例2 例3
证明复变函数项级数 k(k
k 1
sin k z 1)
在z平面上一致收敛。
zk , 设复变函数项级数 k k 1 1 z
性质3 性质4
? 若 z 收 敛 z
n 1 n n 1
n
收敛.
(1) n i (例如 : ) n n 1
绝对收敛级数的和与项 的次序无关。
若级数 an与 bn 都绝对收敛,则
n 1 n 1
a b c ,
n 0 n n 0 n n 0 n
0 0
0
0
注: 对于“缺项”幂级数,也有相应的比值法与根值法。
n 2 n 例4 求 幂 级 数 z 1 z 1 R 1 解 lim n c n
又sn 1 z z z
2
n
n1
1 当 z 1时 , limz 0, limsn . n n 1 z 当 z 1时, lim z n 0, 级数发散. n 1 收敛, 且和函数为 , 当 z 1时; n 综上 z 1 z n 0 发散, 当 z 1时.
设有 zn xn yn,则
级数 zn收敛 xn 和 yn 都收敛。
n 1 n 1 n 1
