高三数学应用题的解法
高三数学应用题解题思路与方法
高三数学应用题解题思路与方法在高三数学应用题中，要正确解题需要掌握一定的解题思路与方法。
本文将针对高三数学应用题，介绍一些解题的思路和方法，帮助同学们更好地应对数学应用题。
一、理清题意和建立数学模型在解决数学应用题之前，首先要理清题意，明确问题的要求和条件。
然后，根据问题的特点，建立与之相对应的数学模型。
数学模型是数学工具与实际问题之间的桥梁，通过建立数学模型，可以将实际问题转化为数学问题，从而用数学方法来解决。
二、分析问题和列出方程在建立好数学模型后，要对问题进行深入分析，找出与问题相关的数学关系。
常见的方法是列方程，通过建立方程式来描述问题中的数学关系。
在列方程时，要根据题目所给的条件和要求，选择适当的变量，并根据变量之间的关系建立相应的方程。
三、解方程和计算在列出方程之后，我们要运用数学方法解方程，求出方程的解。
这一步需要运用到高等数学中的方程求解方法，包括因式分解、配方法、二次方程公式、求根公式等。
根据具体题目的要求和条件，选择适当的方法来解方程，并进行计算。
四、检查答案和解释在解决数学应用题之后，要及时检查答案的合理性。
可以通过将得到的答案代入原方程或者根据题目的特性进行分析，判断答案是否符合题目的要求。
同时，要对解题过程进行解释，详细说明每一步的思路、方法和推理过程，使得解答完整且可读性强。
五、多做练习和总结为了提高解决数学应用题的能力，同学们还需要多做练习，并及时总结经验和方法。
通过做大量的题目，可以熟悉各种类型的数学应用题，熟练掌握解题的思路和方法。
同时，要及时总结解题的经验，归纳出一些常用的解题技巧，为今后的解题提供更为有效的帮助。
总结：高三数学应用题是考试中的重点和难点，要解题，需要通过理清题意、建立数学模型、分析问题和列方程、解方程和计算、检查答案和解释等步骤。
同时，要多做练习和总结经验，提高解题能力。
希望本文的介绍能够帮助同学们更好地应对高三数学应用题，取得好成绩。
高三数学实际生活中的应用问题
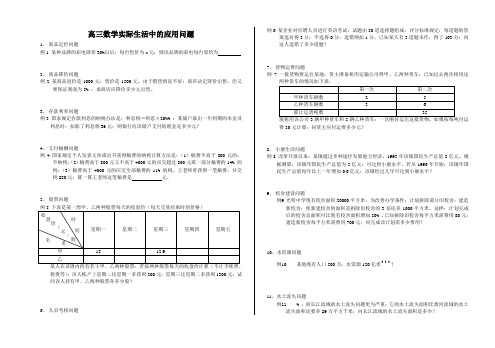
高三数学实际生活中的应用问题1、 商品定价问题例1 某种品牌的彩电降价30%以后：每台售价为a 元：则该品牌的彩电每台原价为2、 商品降价问题例2 某商品进价是1000元：售价是1500元。
由于销售情况不好：商店决定降价出售：但又要保证利润为5% ：求商店应降价多少元出售。
3、 存款利率问题例3 国家规定存款利息的纳税办法是：利息税＝利息×20%% ：某储户取出一年到期的本金及利息时：扣除了利息税36元：则银行向该储户支付的现金是多少元？4、 支付稿酬问题例4 国家规定个人发表文章或出书获得稿费的纳税计算方法是：（1）稿费不高于800元的：不纳税：（2）稿费高于800元又不高于4000元的应交超过800元那一部分稿费的14% 的税：（3）稿费高于4000元的应交全部稿费的11% 的税。
王老师曾获得一笔稿费：并交税280元：算一算王老师这笔稿费是 元。
5、 股票问题某人在该周内持有若干甲、乙两种股票：若按两种股票每天的收盘价计算（不计手续费、税费等）：该人帐户上星期二比星期一多获利200元：星期三比星期二多获利1300元：试问该人持有甲、乙两种股票各多少股？6、 人员考核问题例6 某企业对应聘人员进行英语考试：试题由50道选择题组成：评分标准规定：每道题的答案选对得3分：不选得0分：选错倒扣1分。
已知某人有5道题未作：得了103分：问这人选错了多少道题？7、 货物运费问题例7 一批货物要运往某地：货主准备租用运输公司得甲、乙两种货车：已知过去两次租用这现租用该公司3辆甲种货车和5辆乙种货车：一次刚好运完这批货物。
如果按每吨付运费30元计算：问货主应付运费多少元？8、 小康生活问题例8 改革开放以来：某镇通过多种途径发展地方经济。
1995年该镇国民生产总值2亿元。
根据测算：该镇年国民生产总值为5亿元：可达到小康水平。
若从1996年开始：该镇年国民生产总值每年比上一年增加0.6亿元：该镇经过几年可达到小康水平？9、 校舍建设问题例9 光明中学现有校舍面积20000平方米：为改善办学条件：计划拆除部分旧校舍：建造新校舍：使新建校舍的面积是拆除旧校舍的3倍还多1000平方米。
数学解方程应用题解题技巧
数学解方程应用题解题技巧解方程应用题是数学中的一项重要技能，它不仅考察了我们对数学知识的掌握，还考验了我们的逻辑思维和解决问题的能力。
在这篇文章中，我们将详细介绍解方程应用题的技巧，帮助您在数学学习的道路上更进一步。
一、识别问题，明确目标解方程应用题的第一步是识别问题，明确求解目标。
通常，这类题目会给出一个实际问题的背景，我们需要从中抽象出数学模型，确定未知数，进而列出方程。
二、分析问题，选择合适的解法在明确求解目标后，接下来要分析问题的类型，选择合适的解法。
常见的方程类型有线性方程、一元二次方程、不等式等。
下面我们针对这些类型，介绍一些解题技巧。
1.线性方程线性方程的解法相对简单，主要有代入法、消元法等。
（1）代入法：将一个方程的解代入另一个方程，求解未知数。
（2）消元法：通过加减、乘除等运算，将方程中的某一未知数消去，从而求解另一个未知数。
2.一元二次方程一元二次方程的解法有公式法、配方法、因式分解法等。
（1）公式法：直接应用求根公式求解。
（2）配方法：将一元二次方程配成完全平方形式，求解未知数。
（3）因式分解法：将一元二次方程进行因式分解，求解未知数。
3.不等式不等式的解法有图像法、区间法、高斯消元法等。
（1）图像法：通过绘制函数图像，分析不等式的解集。
（2）区间法：根据不等式的性质，确定解集的区间。
（3）高斯消元法：将不等式转化为方程组，利用消元法求解。
三、验证结果，确保正确性解方程应用题的最后一步是验证结果，确保求解的正确性。
将求得的解代入原方程，检验是否满足题目的要求。
总结：解方程应用题需要我们具备较强的逻辑思维和分析能力。
通过以上介绍的解题技巧，相信您在解决这类问题时会更有信心。
高中数学应用题
高中数学应用题数学应用题涉及社会生活的各个方面，它结合高中数学知识考查学生的阅读理解与数学建模等各种综合解决问题的能力。
下面笔者就结合实例，谈一谈最常用的三种解题策略。
一、化归转化策略数学知识源于生活，而且数学问题与现实问题是息息相关的，化归是运用某种方法或手段，把有待解决的较为生疏或较为复杂的不规范问题转化归结为所熟悉的规范性问题来解决的思想方法。
化归方法的特点在于它具有很强的目的性、方向性、概括性和灵活性。
二、数形结合策略中学阶段学过的解析法、三角法、复数法、向量法、图像法等都属于数形结合的范畴。
很多数学问题给出的条件是比较复杂抽象的数量关系，但通过观察、分析、联想，发现它们具有某些几何特征，或者许多数量关系本身有明确的几何意义。
这些几何特征或几何意义可帮助我们发现数与形之间的新关系，从而获得直观明快的解题思路。
三、模式识别策略许多教师在教学几何证明时，讲得头头是道，有理有据，但学生仍不理解和掌握证明方法。
究其原因，一是忽视学习方法适用的背景和条件的教学，二是缺少对学生认知体验的训练。
因此，学生既不知道什么情况下使用什么方法有效，也无这方面的认知体验。
1.应用题的内容模式根据中学阶段所学知识的实际情况，应用题的内容大致分为以下模式：（1）与函数、方程、不等式有关的应用题，经常涉及路程、物价、产量等实际问题，解答这类问题一般要列出相关解析式，然后用函数、方程、不等式等有关知识和方法加以解决。
（2）与数列有关的应用题，经常涉及与增长率有关的实际问题，需用等差、等比数列和简单的递推知识。
（3）与三角函数有关的应用题，一般涉及航行、测量及物理中的摆动、振动等。
（4）立体几何应用题，如空中的观测，地球的经纬度、面积、体积的计算等实际问题。
（5）与二次曲线有关的应用题，这类问题需要建立坐标系，运用解析几何知识加以解决。
在具体运用模式识别策略时要注意知识的负迁移的影响，要理解问题的实质，在头脑中储存正确的问题模式，建立知识的合理联系，避免生搬硬套。
做数学应用题的技巧
做数学应用题的技巧高数学并不是简简洁单就能学好，升入中学以后，中学数学变得更抽象了，许多学问同学们理解起来起先有困难了。
那么接下来给大家共享一些关于做数学应用题的技巧，盼望对大家有所协助。
做数学应用题的技巧一.归一问题解答含义及方法牢记题中的数量关系，细致阅读应用题给出的意思。
含义:在解容许用题时，先要求出一份是多少(即单一量)，然后以单一量为标准，求出所要求的数量。
这类应用题叫做归一问题。
数量关系：总量÷份数=1份数量1份数量×所占份数=所求几份的数量另一总量÷(总量÷份数)=所求份数解答思路及方法：先求出单一量，以单一量为标准，求出所要求的数量。
二.归总问题解答含义及方法含义：解题时，时时先找出“总数量”，然后再依据其它条件算出所求的问题，叫归总问题。
所谓“总数量”是指货物的总价、几小时(几天)的总工作量、几公亩地上的总产量、几小时行的总路程等。
数量关系：1份数量×份数=总量总量÷1份数量=份数总量÷另一份数=另一每份数量解题思路和方法: 先求出总数量，再依据题意得出所求的数量。
三.和差问题解答含义及方法含义：确定两个数量的和与差，求这两个数量各是多少，这类应用题叫和差问题。
数量关系：大数=(和+差)÷ 2 小数=(和-差)÷ 2解题思路和方法:简洁的题目可以干脆套用公式;困难的题目变通后再用公式。
四.和倍问题解答含义及方法含义：确定两个数的和及大数是小数的几倍(或小数是大数的几分之几)，要求这两个数各是多少，这类应用题叫做和倍问题。
数量关系：总和÷(几倍+1)=较小的数总和-较小的数= 较大的数较小的数×几倍= 较大的数解题思路和方法:简洁的题目干脆利用公式，困难的题目变通后利用公式。
五.差倍问题解答含义及方法含义：确定两个数的差及大数是小数的几倍(或小数是大数的几分之几)，要求这两个数各是多少，这类应用题叫做差倍问题。
高中数学应用题解析技巧
高中数学应用题解析技巧一、数学应用题解析技巧在高中数学学习中，应用题一直是让许多学生头疼的难题。
面对复杂的文字题，很多同学常常感到无从下手，不知道如何解题。
其实，只要掌握一些解题技巧，就能轻松解决数学应用题。
下面就来分享一些高中数学应用题解析技巧。
首先，要仔细阅读题目，理清题意。
有时候，题目中会有一些多余的信息，需要筛选出关键信息。
在阅读题目的过程中，可以用笔标记出关键信息，帮助理清思路。
其次，建立数学模型。
将题目中的情景转化为数学语言，建立数学模型是解决应用题的关键。
可以通过设变量、列方程等方式，将问题转化为数学问题，从而更好地解决问题。
再者，灵活运用数学知识。
在解决应用题时，要灵活运用所学的数学知识，如代数、几何、概率等。
有时候，不同的知识点可以相互结合，帮助解决问题。
最后，检查答案。
在解题过程中，要注意检查每一步的计算是否准确，避免因计算错误导致答案错误。
同时，要检查答案是否符合实际情况，是否符合题目要求。
二、举例说明为了更好地理解高中数学应用题解析技巧，我们来看一个例题：某班学生参加数学竞赛，其中60%的学生参加了数学竞赛，参加竞赛的学生中有30%的学生获奖。
如果共有120名学生参加了数学竞赛，那么获奖学生有多少人？解题步骤如下：1. 首先，设参加数学竞赛的学生总数为x，则有60%的学生参加了数学竞赛，即0.6x=120，解得x=200，即班级总人数为200人。
2. 其次，参加竞赛的学生中有30%的学生获奖，即获奖学生人数为0.3*120=36人。
3. 最后，检查答案，36人是否符合题目要求，即获奖学生人数为36人。
通过以上例题的解析，我们可以看到，掌握了解题技巧后，解决数学应用题并不难。
只要理清题意，建立数学模型，灵活运用数学知识，就能轻松解决各种数学应用题。
三、总结高中数学应用题解析技巧是数学学习中的重要内容，掌握了解题技巧，就能更好地解决各种数学应用题。
在解题过程中，要仔细阅读题目，建立数学模型，灵活运用数学知识，检查答案，从而提高解题效率，提升数学学习成绩。
应用题的解题步骤与方法
应用题的解题步骤与方法一、解答应用题的一般步骤1、审题，也就是理解题意。
要反复读题，弄清已知条件和所求问题。
2、分析数量之间的关系，也就是分析题目中已知量，未知量及所求问题之间的相互关系。
有时可以通过画简单的线段关系图，使数量关系更加简单明了。
3、确定运算顺序，即先算什么、再算什么、最后算什么，并列出算式，算出结果。
4、验算并写出答案。
二、列方程解应用题的一般步骤1、弄清题意，明确已知量和未知量，用字母X表示未知量。
2、找出题目中已知量和未知量之间的等量关系。
3、根据等量关系，列出方程，并解方程。
4、检验并写出答案。
三、列方程解答应用题跟算术方法解答应用题的联系与区别。
联系：列方程解答应用题，需要应用算术里学习的四则运算的相互关系，以及常见的数量关系，因此算术解法是基础，而列方程解应用题是它的发展。
区别：1、两种解答应用题的方法表达方式不同。
列方程是用代数式表示数量关系，关系式中包括未知数X；算术解法则是用算术式子表示数量关系，计算过程不含未知数。
2、解题思路不同。
列方程解应用题是把未知量设为X，与其它已知量一起参加列式，而算术解法只能从已知与已知，已知与未知之间多层次分析思考，需要逆向思维。
3、解题步骤的不同（见解应用题的步骤）四、解答应用题的基本思路1、综合法思路。
从已知条件出发，根据数量关系先选择两个已知条件，提出可以解答的问题，然后把所求出的数量作为新的已知条件，与其它已知条件搭配，再提出可以解答的问题，这样逐步推导，直到求出题目中所要求的结果为止。
2、分析法思路。
从所求问题入手，根据数量关系，找出解答最后结果所需要的条件，把其中一个（或2个）未知条件作为新问题，再寻找解决这个新问题所需要的条件，这样逐步逆推，直到所找条件在应用题中都是已知的为止。
其实在运用分析法的逆推过程中，就是把复杂的应用题分解成几个简单的应用题。
3、综合法解题思路和分析法解题思路是相反的，但在思考过程中，分析和综合的运用并不是孤立的，而是互相联系的，综合中有分析，交叉运用。
高三数学专题复习：应用题的解法
(包括边界).
整理课件
考题剖析 (2) 因为p=100+3(5－x)+2(8－y),所以3x+2y=131－p,设131－p=k, 那么当k最大时，p最小，在图中通过阴影部分区域且斜率为－ 3
2
的直线3x+2y=k中，使k值最大的直线必通过点(10,4)，即当y=4 时，p最小，此时x=10,v=12.5,w=30,p的最小值为93元. ［点评］本题考查运用线性规划知识解决实际问题的能力，
整理课件
应试策略
Ⅱ.数列、不等式应用题，大多以数列知识知识为背景， 所涉及的知识有数列的首项、通项公式、项数、递推公式、前 n项和公式及an与Sn的关系等等；常见的命题点有：平均增 长率、利率（复利）、分期付款、等值增减或等量增减的问 题.常用的数学模型有：⑴构造等差、等比数列的模型，然后 应用数列求和或特殊数列求和求解；⑵利用无穷等比数列的求 和公式求解，往往与极限结合出题；⑶构造数列通项的递推 公式或Sn的递推公式，利用待定系数法或an与Sn的关系求 解，注意n的范围问题；⑷通过类比归纳得出结论，用数学 归纳法或数列的知识求解.
将实际问题转化为数学问题的建模能力.
整理课件
考题剖析
4、甲、乙两公司同时开发同一种新产品，经测算，对于函数f
（x）、g（x），当甲公司投入 x 万元作宣传时，若乙公司投入的
宣传费小于f（x）万元，则乙 公司对这一新产品的开发有失败的
风险，否则没有失败的风 险；当乙公司投入x万元作宣传时，若
甲公司投入的宣传费小于 g（x）万元，则甲公司对这一新产品的
整理课件
考题剖析
由双曲线定义知P点在以A、B为焦点的双曲线
x2 a2
y2 b2
1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
[单选,A2型题,A1/A2型题]下列CT叙述中，错误的是（）A.CT图像是数字图像B.CT成像仍使用X射线CT是多参数成像D.CT扫描层是二维体积E.CT可以进行薄层扫描 [单选]（）是从根源上保证采购质量的重要措施。A.交货准时性B.供应商参与制造商的产品设计过程C.合格供应商D.可靠的送货和特定的包装要求 [问答题,简答题]什么是凝聚和絮凝？它们在发酵液预处理时的作用是什么？ [单选]（）是现代工业中极为有害的破坏因素。A．磨损B．摩擦C．腐蚀D．疲劳 [单选]施工单位应当于()出具工程质量保修书。A.竣工验收合格时B.竣工验收备案时C.提交竣工验收报告时D.提交竣工结算文件时 [单选]化妆品卫生监督条例是（）。A.针对化妆品生产制定的B.针对化妆品经营制定的C.针对卫生监督制定的D.针对化妆品的生产和经营制定的E.针对化妆品生产、经营和监督而制定的 [问答题,简答题]投资帐户是什么？ [单选]减少病原体，去除引起异味的物质，抑制、减少并去除可能导致腐化的物质是（）的处理方法。A.污泥浓缩B.污泥稳定C.污泥调节D.污泥脱水 [填空题]自然资源是人类可以直接或间接利用的存在于自然界的（）或（），与人类生存直接相关的自然资源有（）、（）、（）、（）、（）和（）。 [判断题]供货方已经与需求方签订了现货供货合同，将来交货，但供货方此时尚未购进货源，担心日后购进货源时价格上涨，稳妥的办法是进行买入套期保值。（）A.正确B.错误 [问答题,简答题]照度计 [单选]动脉瘤最有效的治疗方法是（）A.控制高脂饮食B.体育锻炼C.手术切除D.降低血压E.降血脂药物 [单选,A2型题,A1/A2型题]关于孤独症的治疗，错误的是（）A.异常行为的改变和变更B.对孩子行为的宽容和理解C.特别能力的发现、培养和转化D.应用行为分析疗法是高强度的行为疗法E.采用以药物治疗为主、教育和训练为辅的办法 [单选]信托设立最常见的方式是（）。A.仲裁B.合同C.遗嘱D.诉讼 [问答题,简答题]现场抓斗的检查要点及故障维修。 [问答题,简答题]请演示脊柱骨折的搬运方法。 [单选,A1型题]有降血糖及抗利尿作用的药物是（）。A.甲苯磺丁脲B.氯磺丙脲C.格列本脲D.二甲双胍E.苯乙双胍 [填空题]电容器在刚充电瞬间相当于（），当充电时相当一个等效（）。不过它随着放电而减小。 [单选]某居民企业2012年度取得销售货物收入6000万元，当年实际发生与生产经营活动有关的业务招待费30万元，且能提供有效凭证。该企业当年可在企业所得税前扣除的业务招待费为（）万元。A.9.85B.18C.20.15D.30 [多选]关节镜下可观察到的关节结构有（）。A.滑膜形态B.软骨C.韧带D.内外侧半月板E.血管、神经 [单选,A2型题,A1/A2型题]伴环形铁粒幼红细胞增多的难治性贫血，其环形铁粒幼红细胞至少占有核红细胞的（）A.15%B.20%C.25%D.30%E.35% [单选,A1型题]下列关于核心信念的表述正确的是（）A.位于认知表层显著位置B.与早年生活经历有关C.在意识层面被自己所认识D.在中间信念基础上形成E.明显的影响认知模式 [单选,A1型题]婴儿添加离乳食品的一般顺序是（）A.米湖、蛋黄、鱼泥、菜泥B.面条、蛋黄、肉泥、菜泥C.蛋黄、豆腐、鱼泥、菜泥D.米汤、肉泥、菜泥、碎肝E.米饭、肉泥、菜泥、鸡蛋 [单选]单手摇壶的操作要领是（）A.尽量使手腕用力，做到动作连贯B.摇动的力量要小，节奏要慢C.尽量使手臂用力，摇动的力量要小D.摇动的速度要慢，节奏要慢 [单选,A1型题]关于放射性核素显像，以下描述不正确的是（）。A.放射性药物能选择性地分布于特定的器官或病变组织B.放射性药物能均匀性地分布于特定的器官或病变组织C.放射性药物需引入患者体内D.体外描记放射性药物在体内分布图E.属于放射性核素示踪方法 [单选,A2型题,A1/A2型题]小儿可主动而有意识地叫“月D.9个月E.10个月 [单选]导致心源性猝死最常见的原因是（）A.心瓣膜病变B.冠心病C.心肌病变D.高血压性心脏病E.窒息 [单选]当起飞模式接通时：（）A、自动推力自动接通并工作B、自动推力自动接通但不工作C、自动推力不自动接通，发动机由推力杆控制D、自动推力自动接通，发动机由最后的推力目标控制 [多选]撤回承诺的通知（）到达要约人有效。A、在发出后二十四小时之内B、在承诺通知到达要约人之前C、与承诺通知同时D、在合同签订之前 [单选]支气管扩张时，下列哪两个并发症最为多见（）A.脓胸及肺脓肿B.肺脓肿及肺纤维化C.肺气肿及肺脓肿D.肺源性心脏病及肺纤维化E.脑膜炎及肾炎 [单选]比例关系的正确判断方法是（）。A、先定小比例，再定大比例B、先定大比例，再定小比例，小比例服从大比例C、大比例服从小比例D、先定大比例，后定小比例 [单选,A2型题,A1/A2型题]心理测量工具好坏的最基本标志是（）A.常模B.信度和效度C.代表性D.标准化E.以上都不是 [单选]慢性胆囊炎的CT特征性表现是（）A.胆囊大，囊壁水肿，密度低B.胆囊正常大小，肝内胆管扩张C.胆囊小，囊壁增厚D.胆囊大，胆总管扩张E.以上都不是 [问答题,简答题]优质护理服务的内涵是什么？ [单选]预算线向右上方平行移动的原因是（）A．商品X的价格下降了B．商品Y的价格下降了C．商品X和Y的价格按同样的比率下降D．商品X和Y的价格按同样的比率上升 [单选,A2型题,A1/A2型题]溃疡性结肠炎患者最常见的护理诊断是（）A.体液不足B.皮肤完整性受损C.焦虑D.腹泻E.有感染的危险 [单选]（）接口是MSC和VLR间的接口。A.AB.BC.CD.D [单选]在使用动画输出制式里，NTSC表示每秒播放多少帧：（）A．15B．30C．24D．25 [单选]下列哪种疾病容易导致压力负荷过重引起的心衰（）A.主动脉瓣关闭不全B.二尖瓣关闭不全C.动脉导管未闭D.肺动脉瓣狭窄E.甲状腺功能亢进症 [单选,A2型题,A1/A2型题]现有以下物品，施用有机磷农药（除个别农药外）者可事先涂抹哪种于暴露的皮肤处（）.A.硼酸B.肥皂C.细沙D.泥粉E.高锰酸钾