余弦定理
余弦定理及推导-文档
1.1.2 余弦定理
余弦定理定义及公式
余弦定理,是描述三角形中三边长度与一个角的余弦值关系的数学定理。
是勾股定理在一般三角形情形下的推广。
a²=b²+c²-2bccosA
余弦定理证明
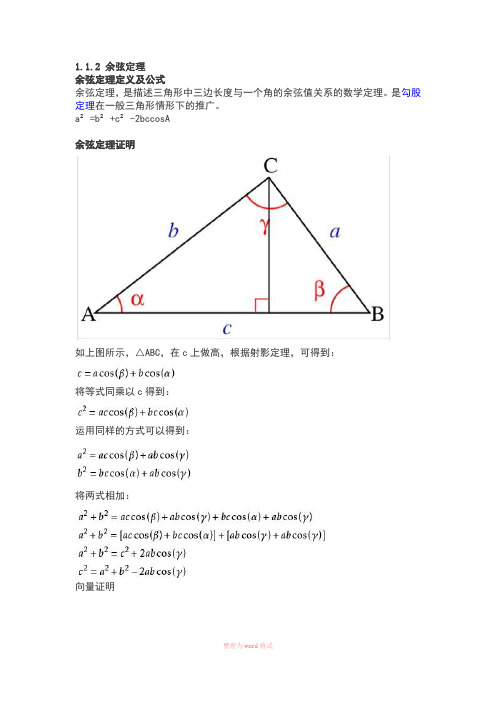
如上图所示,△ABC,在c上做高,根据射影定理,可得到:
将等式同乘以c得到:
运用同样的方式可以得到:
将两式相加:
向量证明
正弦定理和余弦定理
正弦定理
a/sinA=b/sinB=c/sinC=2R
(1)已知三角形的两角与一边,解三角形
(2)已知三角形的两边和其中一边所对的角,解三角形
(3)运用a:b:c=sinA:sinB:sinC解决角之间的转换关系
直角三角形的一个锐角的对边与斜边的比叫做这个角的正弦。
余弦定理
是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值友情提示:本资料代表个人观点,如有帮助请下载,谢谢您的浏览!。
余弦定理的10种证明方法

余弦定理的10种证明方法一、余弦定理余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与他们夹角的余弦的积的两倍,即在ABC ∆中,已知AB c =,BC a =,CA b =,则有2222cos a b c bc A =+-, 2222cos b c a ca B =+-, 2222cos c a b ab C =+-.二、定理证明为了叙述的方便与统一,我们证明以下问题即可:在ABC ∆中,已知AB c =,AC b =,及角A ,求证:2222cos a b c bc A =+-. 证法一:如图1,在ABC ∆中,由CB AB AC =-可得:()()CB CB AB AC AB AC ⋅=-⋅-222AB AC AB AC =+-⋅222cos b c bc A =+-即,2222cos a b c bc A =+-.证法二:本方法要注意对A ∠进行讨论.(1)当A ∠是直角时,由22222222cos 2cos90b c bc A b c bc b c a +-=+-︒=+=知结论成立. (2)当A ∠是锐角时,如图2-1,过点C 作CD AB ⊥,交AB 于点D ,则在Rt ACD ∆中,cos AD b A =,sin CD b A =.从而,cos BD AB AD c b A =-=-.在Rt BCD ∆中,由勾股定理可得: 222BC BD CD =+22(cos )(sin )c b A b A =-+222cos c cb A b =-+即,2222cos a b c bc A =+-.说明:图2-1中只对B ∠是锐角时符合,而B ∠还可以是直角或钝角.若B ∠是直角,图中的图1CAB图2-1DCAB点D 就与点B 重合;若B ∠是钝角,图中的点D 就在AB 的延长线上.(3)当A ∠是钝角时,如图2-2,过点C 作CD AB ⊥,交BA 延长线于点D ,则 在Rt ACD ∆中,cos()cos AD b A b A π=-=-,sin()sin CD b A b A π=-=.从而,cos BD AB AD c b A =+=-.在Rt BCD ∆中,由勾股定理可得:222BC BD CD =+22(cos )(sin )c b A b A =-+222cos c cb A b =-+即,2222cos a b c bc A =+-.综上(1),(2),(3)可知,均有2222cos a b c bc A =+-成立. 证法三:过点A 作AD BC ⊥,交BC 于点D ,则在Rt ABD ∆中,sin BD c α=,cos ADc α=.在Rt ACD ∆中,sin CD b β=,cos ADbβ=.由cos cos()cos cos sin sin A αβαβαβ=+=-可得:2cos AD AD BD CD AD BD CDA c b c b bc-⋅=⋅-⋅=2222AD BD CD bc -⋅=222222c BD b CD BD CD bc -+--⋅=222()2b c BD CD bc +-+=2222b c a bc+-=整理可得2222cos a b c bc A =+-. 证法四:在ABC ∆中,由正弦定理可得sin sin sin sin()a b c cA B C A B ===+. 从而有sin sin b A a B =,………………………………………………………………①sin sin()sin cos cos sin c A a A B a A B a A B =+=+. …………………………②将①带入②,整理可得cos cos a B c b A =-.…………………………………………③ 将①,③平方相加可得22222(cos )(sin )2cos a c b A b A b c bc A =-+=+-.图2-2DBACβα图3DBAC即,2222cos a b c bc A =+-.证法五:建立平面直角坐标系(如图4),则由题意可得点(0,0)A ,(,0)B c ,(cos ,sin )C b A b A ,再由两点间距离公式可得2a =22(cos )(sin )c b A b A -+222cos c cb A b =-+.即,2222cos a b c bc A =+-.证法六:在ABC ∆中,由正弦定理可得2sin a R A =,2sin b R B =,2sin c R C =. 于是,222224sin 4sin ()a R A R B C ==+222224(sin cos cos sin 2sin sin cos cos )R B C B C B C B C =++ 222224(sin sin 2sin sin 2sin sin cos cos )R B C B C B C B C =+-+ 2224(sin sin 2sin sin cos())R B C B C B C =+++ 2224(sin sin 2sin sin cos )R B C B C A =+-22(2sin )(2sin )2(2sin )(2sin )cos R B R C R B R B A =+-222cos b c bc A =+-即,结论成立.证法七:在ABC ∆中,由正弦定理可得2sin a R A =,2sin b R B =,2sin c R C =. 于是,2222cos a b c bc A =+-22222224sin 4sin 4sin 8sin sin cos R A R B R C R B C A ⇔=+-2222sin 2sin 2sin 4sin sin cos A B C B C A ⇔=+- 22sin 2cos 2cos 24sin sin cos A B C B C A ⇔=-+-222cos 22cos()cos()4sin sin cos A B C B C B C A ⇔-=-+--由于cos()cos()cos B C A A π+=-=-,因此2cos cos()cos()2sin sin cos A B C B C B C A ⇔=+-+cos cos()2sin sin A B C B C ⇔=--+cos cos cos sin sin cos()A B C B C B C ⇔=-+=-+. 这,显然成立.xy图4BA(O)C即,结论成立.证法八:如图5,以点C 为圆心,以CA b =为半径作C ,直线BC 与C e 交于点,D E ,延长AB 交C e 于F ,延长AC 交C e 于G .则由作图过程知2cos AF b A =, 故2cos BF b A c =-.由相交弦定理可得:BA BF BD BE ⋅=⋅, 即,(2cos )()()c b A c b a b a ⋅-=+⋅-, 整理可得:2222cos a b c bc A =+-.证法九:如图6,过C 作CD ∥AB ,交ABC ∆的外接圆于D ,则AD BC a ==,BD AC b ==.分别过,C D 作AB 的垂线,垂足分别为,E F ,则cos AE BF b A ==,故2cos CD c b A =-.由托勒密定理可得AD BC AB CD AC BD ⋅=⋅+⋅, 即,(2cos )a a c c b A b b ⋅=⋅-+⋅.整理可得:2222cos a b c bc A =+-.证法十:由图7-1和图7-2可得2a =22(cos )(sin )c b A b A -+, 整理可得:2222cos a b c bc A =+-.bcosA absinAc-bcosAac-bcosAbsinA图7-2图7-1DE DABCC B余弦定理的证明方法还有很多,比如可以用物理方法证明、可以构造相似三角形证明、可以利用图形面积证明等.感兴趣的读者可以到图书馆或互联网中进行查询.bac2bcosA-cb-a bb图5GDE FCAB c b aa 图6F EDCBA。
余弦函数及余弦定理

余弦函数及余弦定理余弦函数及余弦定理是什么余弦定理,其实就是描述三角形中三边长度与一个角的余弦值关系的数学定理。
运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题。
下面小编给大家整理了关于余弦函数及余弦定理的内容,欢迎阅读,内容仅供参考!余弦函数余弦函数的定义域是整个实数集,值域是[-1,1]。
它是周期函数,其最小正周期为2π。
在自变量为2kπ(k为整数)时,该函数有极大值1;在自变量为(2k+1)π时,该函数有极小值-1。
余弦函数是偶函数,其图像关于y轴对称。
余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值。
利用余弦定理,可以解决以下两类有关三角形的问题(1)已知三边,求三个角;(2)已知两边和它们的夹角,求第三边和其他两个角。
正余弦定理的应用1.解三角形时,找三边一角之间的关系常用余弦定理,找两边两角之间的关系常用正弦定理2.根据所给条件确定三角形的形状,主要有两种途径:①化边为角;②化角为边.并常用正余弦定理实施边角转化。
3.用正余弦定理解三角形问题可适当应用向量的数量积求三角形内角与应用向量的模求三角形的边长。
4.应用问题可利用图形将题意理解清楚,然后用数学模型解决问题。
5.正余弦定理与三角函数、向量、不等式等知识相结合,综合运用解决实际问题。
正余弦函数的性质余弦定理多种证明方法余弦定理的证明方法还有很多,比如可以用物理方法证明、可以构造相似三角形证明、可以利用图形。
余弦定理含义

余弦定理含义
余弦定理是在三角形中,描述了三个边和内夹角之间的关系。
它的含义可以总结如下:
在一个三角形ABC中,假设a、b、c分别表示边BC、AC和AB的长度,而角A、角B和角C分别表示对应的内夹角。
那么余弦定理的表达式如下:c^2 = a^2 + b^2 - 2ab·cos(C)。
其中的cos(C)是角C的余弦值。
余弦定理的含义是:对于任意一个三角形,如果我们知道了三个边的长度,那么可以通过余弦定理计算出对应的三个内夹角的余弦值。
反之,如果我们已知三个边的长度以及其中两个夹角的度数,也可以利用余弦定理求解第三个角的度数。
余弦定理在解决三角形相关问题时非常有用,例如计算未知边长或角度、判断三角形的形状(锐角三角形、直角三角形、钝角三角形)等。
它是解决三角学问题的重要工具之一。
三角函数余弦定理公式

三角函数余弦定理公式三角函数余弦定理公式大全余弦定理对于边长为a、b、c而相应角为A、B、C的三角形,有:a^2 = b^2 + c^2 - 2bc·cosAb^2 = a^2 + c^2 - 2ac·cosBc^2 = a^2 + b^2 - 2ab·cosC也可表示为:cosC=(a^2 +b^2 -c^2)/ 2abcosB=(a^2 +c^2 -b^2)/ 2accosA=(c^2 +b^2 -a^2)/ 2bc这个定理也可以通过把三角形分为两个直角三角形来证明。
如果这个角不是两条边的夹角,那么三角形可能不是唯一的(边-边-角)。
要小心余弦定理的这种歧义情况。
延伸定理:第一余弦定理(任意三角形射影定理)设△ABC的三边是a、b、c,它们所对的角分别是A、B、C,则有a=b·cos C+c·cos B,b=c·cos A+a·cos C,c=a·cos B+b·cos A三角函数正弦定理公式正弦定理对于边长为a, b和c而相应角为A, B和C的三角形,有:sinA / a = sinB / b = sinC/c也可表示为:a/sinA=b/sinB=c/sinC=2R变形:a=2RsinA,b=2RsinB,c=2RsinC其中R是三角形的外接圆半径。
它可以通过把三角形分为两个直角三角形并使用上述正弦的定义来证明。
在这个定理中出现的公共数(sinA)/a是通过A, B和C三点的圆的直径的倒数。
正弦定理用于在一个三角形中(1)已知两个角和一个边求未知边和角(2)已知两边及其一边的对角求其他角和边的问题。
余弦定理总结知识点

余弦定理总结知识点首先,我们来看一下余弦定理的数学表达式。
对于一个三角形ABC,余弦定理可以表示为:a^2 = b^2 + c^2 - 2bc * cosAb^2 = a^2 + c^2 - 2ac * cosBc^2 = a^2 + b^2 - 2ab * cosC其中,a、b、c分别表示三角形的三个边的长度,A、B、C分别表示三角形的三个内角的大小,cosA、cosB、cosC分别表示三角形的三个内角的余弦值。
通过这个数学表达式,我们可以看出余弦定理的基本思想是通过三角形中的边长和角度的关系来求解各种三角形问题。
余弦定理的优点是不仅可以用于等腰三角形和等边三角形,还可以适用于一般三角形,因此在实际应用中具有非常广泛的适用性。
余弦定理的应用场景非常广泛,比如在测量地理距离、建筑设计、航海、航空等领域都有着重要的作用。
下面我们来分别介绍一下余弦定理的几种常见应用。
1、求解三角形的边长余弦定理可以通过已知三角形的一个角和两个边长来求解第三条边的长度。
比如,已知三角形的两边长分别为3和4,并且夹角为60度,就可以通过余弦定理来求解第三条边的长度。
根据余弦定理的数学表达式,我们可以得到:c^2 = 3^2 + 4^2 - 2*3*4*cos60°= 9 + 16 - 24*0.5= 25 - 12= 13因此,第三条边的长度为√13。
2、求解三角形的角度余弦定理也可以通过已知三角形的三条边的长度来求解三角形的夹角。
比如,已知三角形的三条边长分别为3、4、5,就可以通过余弦定理来求解各个角的大小。
根据余弦定理的数学表达式,我们可以得到:cosA = (b^2 + c^2 - a^2)/(2bc)= (4^2 + 5^2 - 3^2)/(2*4*5)= (16 + 25 - 9)/40= 32/40= 0.8因此,∠A的余弦值为0.8,所以∠A的大小为cos⁻¹(0.8)≈36.87°。
余弦定理

余弦定理【知识要点】1、余弦定理:在△ABC 中2222222222cos , 2cos ,2cos a b c bc A b a c ac B c a b ab C=+-=+-=+-2、余弦定理的变形:222222222cos ,cos ,cos ,222b c a a c b a b c A B C bc ac ab+-+-+-===3、余弦定理的应用(1)已知△ABC 的两角及夹边,求第三边; (2)已知△ABC 的三边,求角. 【例题分析】1、在△ABC 中,若sin A ∶sin B ∶sin C =7∶8∶13,求∠C 。
2、在△ABC 中,求证:)cos cos (aAb Bc a b b a -=-3、已知(a 2+bc )x 2+2b 2+c 2x +1 = 0是关于x 的二次方程,其中a 、b 、c 是三角形的三边, (1)若∠A 为钝角,试判断方程根的情况; (2)若方程有两个相等的实根,求∠A 的度数.一、选择题1、在△ABC 中,若2lg sin lg cos lg sin lg =--C B A ,则△ABC 的形状是 ( )A 、直角三角形B 、等边三角形C 、不能确定D 、等腰三角形 2、在△ABC 中,若,3))((bc a c b c b a =-+++则A =( )A 、090 B 、060 C 、0135 D 、0150BACabc3、在△ABC 中,若1413cos ,8,7===C b a ,则最大角的余弦是 ( ) A 、51- B 、61- C 、71- D 、81-4.边长为5,7,8的三角形的最大角与最小角的和是( )A 、090 B 、0120 C 、0135 D 、0150 5、在△ABC 中,若=++=A c bc b a 则,222( )A 、120°B 、60°C 、45°D 、30° 6、在△ABC 中,若=+=C B C B A tan tan ,cos cos 2sin 则( )A 、4B 、2C 、3D 、347、在锐角△ABC 中,若2,3a b ==,则边长c 的取值范围是( )A 、B 、(5,23)C 、(3,13)D 、(3,28、在△ABC 中,a =,b =1,c =2,则A 等于 ( )A 、30°B 、45°C 、60°D 、75°9、在△ABC 中,a 、b 、c 分别是三内角A 、B 、C 的对边,且sin 2A -sin 2C =(sinA -sinB)sinB ,则角C 等于( )A 、π6B 、π3 C 、5π6D 、2π310、在△ABC 中,若A =60°,BC =43,AC =42,则角B 的大小为 ( )A 、30°B 、45°C 、135°D 、45°或135°11、在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,A =π3,a =3,b =1,则c = ( ) A 、1B 、2C 、3-1D 、 312、在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,若a =2,b =22,且三角形有两解,则角A 的取值范围是 ( )A 、⎝⎛⎭⎪⎫0,π4B 、⎝ ⎛⎭⎪⎫π4,π2C 、⎝ ⎛⎭⎪⎫π4,3π4D 、⎝ ⎛⎭⎪⎫π4,π313、在△ABC 中,角A 、B 、C 所对的边长分别为a 、b 、c.若∠C =120°,c =2a ,则 ( )A 、a >bB 、a <bC 、a =bD 、a 与b 的大小关系不能确定14、在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c ,若a 2-b 2=3bc ,sinC =23sinB ,则A = ( )A 、30°B 、60°C 、120°D 、150°15、在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tanB =3ac ,则角B 的值为 ( )A 、π6B 、π3 C 、π6或5π6D 、π3或2π316、已知△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边,如果a 、b 、c 成等差数列,∠B =30°,△ABC 的面积为0.5,那么b 为 ( )A 、1+ 3B 、3+ 3C 、3+33D 、2+ 317、在△ABC 中,cos 2B2=a +c 2c(a 、b 、c 分别为角A 、B 、C 的对边),则△ABC 的形状为 ( )A 、直角三角形B 、正三角形C 、等腰三角形D 、等腰三角形或直角三角形18、在△ABC 中,tanA =12,cosB =31010,若最长边为1,则最短边的长为 ( )A 、455B 、355 C 、255D 、55二、填空题19、若在△ABC 中,060,1,ABC A b S ∆∠==则CB A cb a sin sin sin ++++=_______。
正弦余弦定理公式

正弦余弦定理公式
正弦定理:设三角形的三边为a b c,他们的对角分别为a b c,外接圆半径为r,则称关系式a/sina=b/sinb=c/sinc为正弦定理。
余弦定理:设三角形的三边为a b c,他们的对角分别为a b c,则称关系式,a^2=b^2+c^2-2bc*cosa。
正弦定理:设三角形的三边为a b c,他们的对角分别为a b c,外接圆半径为r,则称关系式a/sina=b/sinb=c/sinc为正弦定理。
余弦定理:设立三角形的三边为a b c,他们的对角分别为a b c,则表示关系式
a^2=b^2+c^2-2bc*cosa
b^2=c^2+a^2-2ac*cosb
c^2=a^2+b^2-2ab*cosc。
证明:
任意三角形abc,作abc的外接圆o。
并作直径bd交⊙o于d,相连接da.
因为直径所对的圆周角是直角,所以∠dab=90度,
因为同弧所对的圆周角成正比,所以∠d等同于∠c。
所以c/sinc=c/sind=bd=2r。
相似可以证其余两个等式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c^2=(a-b)·(a-b)=a^2+b^2-2a·b=|a|^2+|b|^2-2|a||b|cos<a,b>
=> c^2=a^2+b^2-2abcosC
粗体为向量,正常字体指的是边长
平面几何证法
在任意△ABC中
做AD⊥BC.
∠C所对的边为c,∠B所对的边为b,∠A所对的边为a
1:在钝角三角形中,钝角对边上的正方形,比钝角两夹边上的正方形之和大一个矩形的两倍,这个矩形就是由一锐角向对边的延长线做垂线,垂足到钝角之间一段与另一边所构成的矩形。
2:在锐角三角形中,锐角对边上的正方形,比锐角两夹边上的正方形之和小一个矩形的两倍,这个矩形就是由一锐角向对边做垂线,垂足到原锐角顶点之间的一段与该边所构成的矩形。[1]
这事一下子就得跳到古希腊时期,正如我们所知道的,由毕氏学派发现了勾股定理的一般形式。勾股定理在西方也就被冠以“毕达哥拉斯定理”的称号,在中国,最早记录勾股定理的文献,应该是《周髀算经》。不管怎么说,勾股定理的形式也就完全确定下来,至此以后就再也没有变过。但对其不断的证明和探索却没有停止,直到现在依然如此——爱因斯坦就是因为他独立证明出了勾股定理,产生出了对数学的兴趣,由此走上科学之路,有不明真相的童鞋据此写下这样一个等式:E=Mc=M(a+b)。
与我们知道的不同,古时的勾股定理并非如我们现在的形式——两直角边平方和等于斜边的平方。古希腊人对几何的崇拜,使得勾股定理的描述形式在很长一段时间里都是几何语言——两直角边上的正方形面积之和等于斜边上的正方形面积。所以有后人对其表述形式作出了推广,比如将正方形改成三个相似图形。
由于勾股定理作用在直角三角形中如此有效,人们自然会想到一般的三角形会不会由此类似的结论,对余弦定理的探讨由此展开。当然,由于在古代尚未发展处“三角函数”,甚至于连角度的概念都没有完全形成,所以所出现的余弦定理都只是现代余弦定理的几何等价形式。比如古希腊时期欧几里得,在其《几何原本》里就阐述了几条余弦定理的等价命题:
余弦定理对于任意三角形,若三边为a,b,c三角为A,B,C—,则满足性质—
a^2 = b^2 + c^2 - 2·b·c·cosA
b^2 = a^2 + c^2 - 2·a·c·cosB
c^2 = a^2 + b^2 - 2·a·b·cosC
cosC = (a^2 + b^2 - c^2) / (2·a·b)
b^2=c^2+a^2-2ac*cosB
作用
(1)已知三角形的三条边长,可求出三个内角
(2)已知三角形的两边及夹角,可求出第三边。
(3)已知三角形两边及其一边对角,可求其它的角和第三条边。(见解三角形公式,推导过程略。)
判定定理一(两根判别法):
若记m(c1,c2)为c的两值为正根的个数,c1为c的表达式中根号前取加号的值,c2为c的表达式中根号前取
余弦定理的前世
如果要算起最古老的数学定理,那自是勾股定理——远在几千年前的巴比伦时期就已经存在;要算起证明方法最多的数学定理,那也是勾股定理——有四五百种方法,爱因斯坦,美国总统这些人都参与进来。今日让我们简单回味一下勾股定理的前世今生,对这伟大的数学定理重新瞻仰。
勾股定理的最早记录,来自美索不达米亚时期的数学泥版。在一块泥版上,刻着“构成直角三角形的各边长”,比如(3,4,5),(5,12,13)等,这大概是最早的毕达哥拉斯数组的最早记录,虽然其远在毕达哥拉斯之前。不过,巴比伦人并没有将之写成统一的数学形式,他们只是将这些数组列成表格,方便计算。很显然,这个时期的数学都是为了解决实际问题。而且严格来说,巴比伦人也没有发现真正的勾股定理,但这作为勾股定理的雏形是绝对有道理的,因为毕达哥拉斯本人都很有可能是从巴比伦人那里学到了勾股定理。
cosB = (a^2 + c^2 - b^2) / (2·a·c)
cosA = (c^2 + b^2 - a^2) / (2·b·c)
(物理力学方面的平行四边形定则以及电学方面正弦电路向量分析也会用到)
第一余弦定理(任意三角形射影定理)
设△ABC的三边是a、b、c,它们所对的角分别是A、B、C,则有
解三角形公式
例如:已知△ABC的三边之比为5:4:3,求最大的内角。
解设三角形的三边为a,b,c且a:b:c=5:4:3.
由三角形中大边对大角可知:∠A为最大的角。由余弦定理
cos A=0
所以∠A=90°.
再如△ABC中,AB=2,AC=3,∠A=60度,求BC之长。
解由余弦定理可知
BC2=AB2+AC2-2AB×AC·cos A
=4+9-2×2×3×cos60
=13-12x0.5
=13-6
=7
所以BC=√7. (注:cos60=0.5,可以用计算器算)
以上两个小例子简单说明了余弦定理的作用。
其他
从余弦定理和余弦函数的性质可以看出,如果一个三角形两边的平方和等于第三边的平方,那么第三边所对的角一定是直角,如果小于第三边的平方,那么第三边所对的角是钝角,如果大于第三边的平方,那么第三边所对的角是锐角。即,利用余弦定理,可以判断三角形形状。同时,还可以用余弦定理求三角形边长取值范围。
③当b=a且cosA>0(即A为锐角)时,则有一解
④当b=a且cosA<=0(即A为直角或钝角)时,则有零解(即无解)
⑤当b<a时,则有一解
二当a=bsinA时
①当cosA>0(即A为锐角)时,则有一解
②当cosA<=0(即A为直角或钝角)时,则有零解(即无解)
三当a<bsinA时,则有零解(即无解)
解三角形时,除了用到余弦定理外还常用正弦定理。
30°
45°
60°
75°
Sin
1/2
√2/2
√3/2
(√6+√2)/4
Cos
√3/2
√2/2
1/2
(√6-√2)/4
Tan
√3/3
1
√3
2+√3
先考虑怎样计பைடு நூலகம்三角形第三边的长
实际应用
在实际生活中,余弦定理是在计算机应有技术中的智能推荐系统,新闻分类中的基本算法之一。从吴军的《数学之美》那本书上知道余弦公式是可以对新闻进行分类的,当然就可以用来对用户进行分类了。引用《数学之美》文章中的话:“向量实际上是多维空间中有方向的线段。如果两个向量的方向一致,即夹角接近零,那么这两个向量就相近。而要确定两个向量方向是否一致,这就要用到余弦定理计算向量的夹角了。”“当两条新闻向量夹角的余弦等于一时,这两条新闻完全重复(用这个办法可以删除重复的网页);当夹角的余弦接近于一时,两条新闻相似,从而可以归成一类;夹角的余弦越小,两条新闻越不相关。”同理,可以在推荐系统中用来计算用户或者商品的相似性。
减号的值
①若m(c1,c2)=2,则有两解
②若m(c1,c2)=1,则有一解
③若m(c1,c2)=0,则有零解(即无解)。
注意:若c1等于c2且c1或c2大于0,此种情况算到第二种情况,即一解。
判定定理二(角边判别法):
一当a>bsinA时
①当b>a且cosA>0(即A为锐角)时,则有两解
②当b>a且cosA<=0(即A为直角或钝角)时,则有零解(即无解)
则有BD=cosB*c,AD=sinB*c,DC=BC-BD=a-cosB*c
根据勾股定理可得:
AC^2=AD^2+DC^2
b^2=(sinB*c)^2+(a-cosB*c)^2
b^2=(sinB*c)^2+a^2-2ac*cosB+(cosB)^2*c^2
b^2=(sinB^2+cosB^2)*c^2-2ac*cosB+a^2
a=b·cos C+c·cos B,b=c·cos A+a·cos C,c=a·cos B+b·cos A。
编辑本段证明方法
平面向量证法(此方法简洁有力,充分体现了向量运算的威力和魅力。不能因为向量比余弦定理晚出现就觉得这个方法不妥当,因为向量的定义中不存在余弦定理,也就是说:向量的正确性不立足于在余弦定理,所以用向量证明余弦定理不存在逻辑问题。况且指数也比对数晚出现,可是如今定义对数用的就是指数方法。只要方法更优,逻辑上没有问题,我们尽可能追求简洁。)
