2017届高三复习：数列大题训练50题及答案

合集下载

北京市2017届高三数学理一轮复习专题突破训练：数列含答案

北京市2017届高三数学理一轮复习专题突破训练数列一、选择、填空题1、（2016年北京高考)已知{}na 为等差数列,nS 为其前n 项和，若16a=，350a a +=，则6=S _______。

.2、（2015年北京高考）设{}na 是等差数列。

下列结论中正确的是A.若021>+a a，则032>+a aB 。

若031>+a a,则021<+a aC 。

若210a a<<，则312a a a > D 。

若01<a，则()0)(3212>--a a a a3、（2014年北京高考）若等差数列{}na 满足7890a a a ++>，7100a a +<，则当n =______时，{}na 的前n 项和最大.4、（朝阳区2016届高三二模）为了响应政府推进“菜篮子”工程建设的号召,某经销商投资60万元建了一个蔬菜生产基地.第一年支出各种费用8万元,以后每年支出的费用比上一年多2万元。

每年销售蔬菜的收入为26万元。

设()f n 表示前n 年的纯利润(()f n =前n 年的总收入－前n 年的总费用支出－投资额）,则()f n = （用n 表示）;从第年开始盈利.5、（东城区2016届高三二模）成等差数列的三个正数的和等于6,并且这三个数分别加上3、6、13后成为等比数列{}nb 中的b 、b 、b ，则数列{}nb 的通项公式为A.12n n b -= B 。

13n n b -= C 。

22n n b -=D 。

23n n b -=6、（丰台区2016届高三一模）若数列{}na 满足*12(0,)N n n na a a n，且2a 与4a 的等差中项是5,则12n aa a 等于（A)2n（B ）21n（C ）12n (D ）121n7、(海淀区2016届高三二模）在数列{}na 中，12a=，且1(1)nn n ana ++=，则3a的值为A 。

湖北省各地2017届高三最新考试数学理试题分类汇编：数列含答案精品

湖北省各地2017届高三最新考试数学理试题分类汇编数列2017.02一、选择、填空题1、（黄冈市2017届高三上学期期末）设数列{}n a 满足122,6a a ==，且2122n n n a a a ++-+=，若[]x 表示不超过x 的最大整数，则122017201720172017a a a ⎡⎤+++=⎢⎥⎣⎦. 2、（荆、荆、襄、宜四地七校考试联盟2017届高三2月联考）“斐波那契”数列由十三世纪意大利数学家斐波那契发现．数列中的一系列数字常被人们称之为神奇数．具体数列为：1,1,2,3,5,8，即从该数列的第三项数字开始，每个数字等于前两个相邻数字之和．已知数列{}n a 为“斐波那契”数列，n S 为数列{}n a 的前n 项和，则（Ⅰ）7S =__________；（Ⅱ）若2017a m =，则2015S =__________．（用m 表示） 3、（荆州市五县市区2017届高三上学期期末）已知数列{}n a 的前n 项和为n S ，且满足41n n S a =+*()n ∈N ，设3log ||n n b a =，则数列{}n b 的通项公式为________.4、（襄阳市2017届高三1月调研）在等差数列{}n a 中，已知123249,21a a a a a ++==，数列{}n b 满足()12121211,2n n n n n b b b n N S b b b a a a *+++=-∈=+++，若2n S >，则n的最小值为A. 5B. 4C. 3D. 25、（襄阳市优质高中2017届高三1月联考）已知121,,,9a a --成等差数列，1239,,,,1b b b --成等比数列，则()221b a a -的值为 A. 8 B. 8- C. 8± D.98±6、（孝感市七校教学联盟2017届高三上学期期末）现有10个数，它们能构成一个以1为首项，3-为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是 .7、（湖北省部分重点中学2017届高三上学期第二次联考）在等差数列{}n a 中，36954a a a ++=，设数列{}n a 的前n 项和为n S ，则11S =A. 18B. 99C. 198D. 2978、（荆州中学2017届高三1月质量检测）已知数列{}n a 为等差数列，满足32015OA a OB a OC =+uu r uur uu u r，其中,,A B C 在一条直线上，O 为直线AB 外一点，记数列{}n a 的前n 项和为n S ，则2017S 的值为（） A.20172 B. 2017 C. 2016 D. 201529、（荆州中学2017届高三1月质量检测）对于数列{}n a ，定义na a a Hn nn 12122-+++=为{}n a 的“优值”.现在已知某数列{}n a 的“优值”12+=n Hn ，记数列{}n a kn -的前n 项和为n S ，若6n S S ≤对任意的正整数n 恒成立，则实数k 的取值范围是二、解答题1、（黄冈市2017届高三上学期期末）已知数列{}n a 的前n 项和1122n n n S a -⎛⎫=--+ ⎪⎝⎭，n为正整数.（1）令2n n n b a =，求证：数列{}n b 为等差数列，并求出数列{}n a 的通项公式；（2）令121,n n n n n c a T c c c n+==+++，求n T .2、（荆门市2017届高三元月调考）已知数列{}n a 的前n 项和为n S ，11=a ，当2n ≥时，2)1(2-+=n n a n S .（Ⅰ）求2a ，3a 和通项n a ；（Ⅱ）设数列{}n b 满足12-⋅=n n n a b ，求{}n b 的前n 项和n T .3、（荆州市五县市区2017届高三上学期期末）已知等差数列{}n a 的前n 项和为n S ，且623518,3n n S S a a =+=，数列{}n b 满足124n S n b b b =.（Ⅰ）求数列{}n a ，{}n b 的通项公式；（Ⅱ）令2log n n c b =，且数列11n n c c +⎧⎫⎨⎬⎩⎭的前n 项和为n T ，求2016T .4、（天门、仙桃、潜江市2017届高三上学期期末联合考试）已知函数()x f x a =的图象过点1(1,)2，且点2(1,)()n a n n n*-∈N 在函数()x f x a =的图象上．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）令112n n n b a a +=-，若数列{}n b 的前n 项和为n S ，求证5n S <.5、（武汉市2017届高三毕业生二月调研考）已知数列{}n a 的前n 项和为n S ，0n a >，且满足()22441,.n n a S n n N *+=++∈（1）求1a 及通项公式n a ；（2）若()1nn n b a =-，求数列{}n b 的前n 项和n T .6、（武汉市武昌区2017届高三1月调研）设等差数列{}n a 的前n 项和为n S ，已知19a =，2a 为整数，且5n S S ≤ .（Ⅰ）求{}n a 的通项公式；（Ⅱ）设数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为nT ，求证：49n T ≤.7、（襄阳市2017届高三1月调研）设各项均为正数的等比数列{}n a 中，132464,72.a a a a =+= (1)求数列{}n a 的通项公式； (2))设21log n nb n a =，n S 是数列{}n b 的前n 项和，不等式()log 2n a S a >-对任意正整数n 恒成立，求实数a 的取值范围.8、（孝感市七校教学联盟2017届高三上学期期末）已知数列{n a }的前n 项和为n s ,且1a =2，n +1n a =2(n+1)n a（1）记=nn a b n，求数列{n b }的通项公式；（2）求通项n a 及前n 项和n s .9、（湖北省部分重点中学2017届高三上学期第二次联考）已知等差数列{}n a 满足()()()()()1223121.n n a a a a a a n n n N *+++++++=+∈（1）求数列{}n a 的通项公式；（2）求数列12n n a -⎧⎫⎨⎬⎩⎭的前n 项和n S .10、（荆州中学2017届高三1月质量检测）已知数列{}n a 的前n 项和238n S n n =+，{}n b 是等差数列，且1.n n n a b b +=+ （Ⅰ）求数列{}n b 的通项公式；（Ⅱ）令1(1)(2)n n n nn a c b ++=+，求数列{}n c 的前n 项和n T .参考答案一、选择、填空题1、20162、（Ⅰ）33 （Ⅱ）1m -3、n b n =-4、B5、A6、357、C 8、A 9、167[,]73二、解答题 1、解：（I ）在中，令n=1，可得，即当时，，.又数列是首项和公差均为1的等差数列.于是.……6分(II)由（I ）得，所以由①-②得……12分2、(I)11=a ，当2n =时，22222(1)32S a a =+=-，则24a =，当3n =时，24)41(22333-=++=a a S ，则63=a ，………………2分当2n ≥时，2)1(2-+=n n a n S ，∴当3n ≥时，2211-=--n n na S ， ∴当3n ≥时，n n n n n a na a n S S 2)1()(211=-+=---，即3n ≥时，1)1(-=-n n na a n ，所以11-=-n an a n n ， …………………4分因为22323==a a ，111=a ，所以11n n a a n n -==-…32232a a===，因此，当2n ≥时，n a n 2=，故1,(1),2,(2)n n a n n =⎧=⎨⎩≥. ……………6分(Ⅱ)由(I)可知，1,(1),2,(2)n nn b n n =⎧=⎨⋅⎩≥，所以当1=n 时，11==b T n ，…………8分当2n ≥时，12n T b b =++…2312232n b +=+⨯+⨯+…2n n +⋅，则34222232n T =+⨯+⨯+…1(1)22n n n n ++-⋅+⋅，作差得：3418(22n T =--++…112)2(1)21n n n n n ++++⋅=-⋅+ 故12)1(1+⋅-=+n n n T ，)(+∈N n . ……………………………………………………12分3、解：（Ⅰ）设数列{}n a 的公差为d ，则[]11116155(2)18(1)(31)3(1)(2)a d a d a n d a n d +=++⎧⎪⎨+-=+-⎪⎩由（1）得12590a d -+=， ·················· 2分由（2）得1a d =，联立得13a d ==， ············· 3分所以3n a n =. ························· 4分易知164b =， ························ 5分当2n ≥时11214n S n b b b --=，又124n S n b b b =，两式相除得64(2)n n b n =≥， ················· 7分 164b =满足上式，所以64n n b =. ··············· 8分（Ⅱ）2log 646n n c n ==，111111()36(1)361n n c c n n n n +==-++， 10分11(1)361n T n =-+， ····················· 11分因此2016562017T =. ····················· 12分 4、【解析】（Ⅰ）∵函数()x f x a =的图象过点1(1,)2， ∴11,()()22x a f x ==………………………………………………2分又点2(1,)()n a n n n*-∈N 在函数()x f x a =的图象上从而2112n n a n -=，即212n n n a -=……………………………………6分（Ⅱ）证明：由22(1)21222n n n n n n n b ++=-= 得23521222n n n S +=+++………………………………8分则231135212122222n n n n n S +-+=++++ 两式相减得， 23113111212()222222n n n n S ++=++++- ∴2552n nn S +=-…………………………………………11分∴5n S <……………………………………………………12分5、6、解：（Ⅰ）由19a =，2a 为整数可知，等差数列{}n a 的公差d 为整数，由5n S S ≤,知560,0a a ≥≤，于是940d +≥ ，950d +≤，d 为整数，2d ∴=-.故{}n a 的通项公式为112n a n =-…………6分（Ⅱ）由（Ⅰ），得()()11111111292292112n n a a n n n n +⎛⎫==- ⎪----⎝⎭， 1111111111......27957921122929n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴=-+-++-=- ⎪ ⎪ ⎪ ⎪⎢⎥---⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ，令192n b n =-，由函数()192f x x=-的图象关于点()4.5,0对称及其单调性，知12340b b b b <<<<，567...0b b b <<<<，41n b b ∴≤=.1141299n T ⎛⎫∴≤-= ⎪⎝⎭………12分7、(Ⅰ)解：设数列{a n }的公比为q ，则错误！未找到引用源。

2017年高考试题分类汇编(数列)

2017年高考试题分类汇编（数列）考点1 等差数列1.（2017·全国卷Ⅰ理科）记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为 CA ．1B ．2C ．4D ．82.（2017·全国卷Ⅱ理科）等差数列{}n a 的前n 项和为n S ，33a =，410S =，则11nk kS ==∑ ． 21n n + 3.（2017·浙江）已知等差数列{}n a 的公差为d ,前n 项和为n S ,则“0d >”是 “465+2S S S >”的 CA.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件考点2等比数列1.（2017·全国卷Ⅲ理科）设等比数列{}n a 满足121a a +=-,133a a -=-，则4a =____．8-2.（2017·江苏卷）等比数列{}n a 的各项均为实数，其前n 项的和为n S ，已知374S =,6634S =，则8a = . 32 3.（2017·全国卷Ⅱ理科）我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯 BA ．1盏B ．3盏C ．5盏D ．9盏考法3 等差数列与等比数列综合1.（2017·全国卷Ⅲ理科）等差数列{}n a 的首项为1，公差不为0．若2a ，3a ，6a 成等比数列，则{}n a 前6项的和为 AA ．24-B ．3-C ．3D ．82.（2017·北京理科）若等差数列{}n a 和等比数列{}n b 满足11a b ==-,44a b =8=，则22a b =____. 1 3.（2017·全国卷Ⅰ文科）记n S 为等比数列{}n a 的前n 项和，已知22S =，36S =-. （Ⅰ）求{}n a 的通项公式；(2)n n a =-（Ⅱ）求n S ，并判断1n S +，n S ，2n S +是否成等差数列.4.（2017·全国卷Ⅱ文科）已知等差数列{}n a 的前n 项和为n S ，等比数列{}n b 的前n 项和为n T .11a =-，11b =，222a b +=.（Ⅰ）若335a b +=，求{}n b 的通项公式； 12n n b -= （Ⅱ）若321T =，求3S . 321S =或36S =-.5.（2017·北京文科）已知等差数列{}n a 和等比数列{}n b 满足111a b ==,24a a +10=，245b b a ⋅=．（Ⅰ）求{}n a 的通项公式；21n a n =- , （Ⅱ）求和：13521n b b b b -++++．312n T -=.6.（2017·天津理科）已知{}n a 为等差数列，前n 项和为()n S n *∈N ，{}n b 是首项为2的等比数列，且公比大于0，2312b b +=,3412b a a =-，11411S b =. （Ⅰ）求{}n a 和{}n b 的通项公式； 32n a n =-，2n n b = （Ⅱ）求数列221{}n n a b -的前n 项和()n *∈N . 1328433n n n T +-=⨯+ 7.（2017·天津文科）已知{}n a 为等差数列，前n 项和为*()n S n ∈N ，{}n b 是首项为2的等比数列，且公比大于0，2312b b +=,3412b a a =-,11411S b =. （Ⅰ）求{}n a 和{}n b 的通项公式； 32n a n =-，2n n b = （Ⅱ）求数列2{}n n a b 的前n 项和*()n ∈N . 2(34)216n n T n +=-⨯+8.（2017·山东理科）已知{}n x 是各项均为正数的等比数列，且123x x +=，322x x -=．（Ⅰ）求数列{}n x 的通项公式； 12n n x -=（Ⅱ）如图，在在平面直角坐标xOy 中，依次连接点11(,1)P x ，22(,1)P x ，,11(,1)n n P x n +++得到折线121n PP P +，求由该折线与直线0y =，1x x =，1n x x +=所围成的区域面积n T ．1211222n n n T --=⨯+9.（2017·山东文科）已知{}n a 是各项均为正数的等比数列，且126a a +=,123a a a =.（Ⅰ）求数列{}n a 通项公式； 2n n a =（Ⅱ）{}n b 为各项非零的等差数列,其前n 项和n S ,已知211n n n S b b ++=,求数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和n T . 15(25)()2n n T n =-+⨯考法4 一般数列1.（2017·全国卷Ⅲ文科）设数列{}n a 满足123(21)2n a a n a n +++-=.（Ⅰ）求{}n a 的通项公式；221n a n =- （Ⅱ）求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和. 221n n S n =+。

(完整版)2017高考数列专题复习(精典版知识点+大题分类+选择题+答案详解)

文科数列专题复习一、等差数列与等比数列1。

基本量的思想：常设首项、（公差）比为基本量，借助于消元思想及解方程组思想等。

转化为“基本量”是解决问题的基本方法。

2.等差数列与等比数列的联系1）若数列{}n a 是等差数列，则数列}{n a a 是等比数列，公比为d a ，其中a 是常数，d 是{}n a 的公差。

(a 〉0且a ≠1）； 2）若数列{}n a 是等比数列，且0n a >,则数列{}log a n a 是等差数列，公差为log a q ，其中a 是常数且0,1a a >≠，q 是{}n a 的公比。

3）若{}n a 既是等差数列又是等比数列,则{}n a 是非零常数数列。

4、典型例题分析【题型1】等差数列与等比数列的联系例1 （文16）已知{a n｝是公差不为零的等差数列，a1＝1，且a1，a3，a9成等比数列.（Ⅰ）求数列｛a n｝的通项;（Ⅱ）求数列｛2an}的前n项和S n.解：（Ⅰ）由题设知公差d≠0，由a1＝1，a1，a3,a9成等比数列得121d+＝1812dd++，解得d＝1，d＝0（舍去），故{a n｝的通项a n＝1+（n－1）×1＝n. (Ⅱ）由（Ⅰ）知2m a=2n，由等比数列前n项和公式得S m=2+22+23+…+2n=2(12)12n--=2n+1-2。

小结与拓展:数列{}n a是等差数列，则数列}{n a a是等比数列，公比为d a,其中a是常数，d是{}n a的公差.（a>0且a≠1）.【题型2】与“前n项和Sn与通项an”、常用求通项公式的结合例2 已知数列｛a n}的前三项与数列{b n｝的前三项对应相同，且a1＋2a2＋22a3＋…＋2n－1a n＝8n对任意的n∈N＊都成立，数列｛bn＋1－b n｝是等差数列．求数列｛a n}与{b n}的通项公式。

解：a1＋2a2＋22a3＋…＋2n－1a n＝8n(n∈N＊）①当n≥2时，a1＋2a2＋22a3＋…＋2n－2a n－1＝8(n－1)(n∈N*）②①－②得2n－1a n＝8，求得a n＝24－n,在①中令n＝1,可得a1＝8＝24－1,∴a n＝24－n（n∈N*)．由题意知b1＝8，b2＝4,b3＝2，∴b2－b1＝－4，b3－b2＝－2，∴数列{b n＋1－b n｝的公差为－2－（－4)＝2,∴b n＋1－b n＝－4＋（n－1)×2＝2n－6，法一（迭代法）b n＝b1＋(b2－b1）＋(b3－b2）＋…＋(b n－b n－1）＝8＋（－4)＋(－2）＋…＋（2n－8）＝n2－7n＋14（n∈N＊）．法二（累加法)即b n－b n－1＝2n－8，b n－1－b n－2＝2n－10，…b3－b2＝－2，b2－b1＝－4,b1＝8,相加得b n＝8＋(－4）＋(－2）＋…＋（2n－8)＝8＋（n －1）（－4＋2n －8）2＝n 2－7n ＋14(n∈N ＊）．小结与拓展:1）在数列{a n ｝中，前n 项和S n 与通项a n 的关系为：⎩⎨⎧∈≥-===-)N n ,2( )1(111n S S n S a a n n n 。

普通高中2017高考高三数学第一次模拟试题精选：数列04含答案

数列045、设3x x f =)(，等差数列{}n a 中73=a ，12321=++a a a ，记n S =()31+n a f ，令n n n S a b =，数列}1{nb 的前n 项和为n T . （1）求{}n a 的通项公式和n S ；（2）求证：31<n T ；（3）是否存在正整数n m ,，且n m <<1，使得n m T T T ,,1成等比数列？若存在，求出n m ,的值，若不存在，说明理由.【答案】解：（1）设数列{}n a 的公差为d ，由7213=+=d a a , 12331321=+=++d a a a a .解得11=a ，d =3 ， ……………2分 ∴23-=n a n ……………4分∵3x x f =)(， ∴S n =()31+n a f =131+=+n a n . ……………6分（2）)13)(23(+-==n n S a b n n n∴)131231(31)13)(23(11+--=+-=n n n n b n ……………8分 ∴31)1311(31<+-=n T n ……………10分（3）由(2)知，13+=n n n T ∴13,411+==m m T T m ，13+=n n n T ，∵n m T T T ,,1成等比数列. ∴ 1341)13(2+=+n n m m ……………12分即n n m m 4312+=+6当1=m 时，7n n 43+=，n =1，不合题意；当2=m 时，413n n 43+=，n =16，符合题意；当3=m 时，919n n 43+=，n 无正整数解；当4=m 时，1625n n 43+=，n 无正整数解；当5=m 时，2531n n 43+=，n 无正整数解；当6=m 时，3637n n 43+=，n 无正整数解； ……………15分当7≥m 时，010)3(1622>--=--m m m ，则1162<+m m ，而34343>+=+n n n ，所以，此时不存在正整数m,n,且1<m<n,使得n m T T T ,,1成等比数列. ……………17分综上，存在正整数m=2,n=16,且1<m<n,使得n m T T T ,,1成等比数列. ……………18分另解：（3）由(2)知，13+=n n n T ∴13,411+==m m T T m ，13+=n n n T ∵n m T T T ,,1成等比数列. ∴ 21()31431m n m n =⋅++， ……………12分取倒数再化简得n n mm 4312+=+6 当2=m 时，413n n 43+=，n =16，符合题意； ……………14分 2221161611193,0,39339m m m m m m m +⎛⎫≥<≤=+=+-≤< ⎪⎝⎭时，而34343>+=+nn n ，所以，此时不存在正整数m 、n , 且1<m<n,使得n m T T T ,,1成等比数列. ……………17分综上，存在正整数m=2,n=16,且1<m<n,使得n m T T T ,,1成等比数列. ……………18分6、设等差数列}{n a 的前n 项和为n S ，且34135=+a a ，93=S ．数列}{n b 的前n 项和为n T ，满足n n b T -=1．（1）求数列}{n a 的通项公式；（2）写出一个正整数m ，使得91+m a 是数列}{n b 的项；（3）设数列}{n c 的通项公式为ta a c n n n +=，问：是否存在正整数t 和k （3≥k ），使得1c ，2c ，k c 成等差数列？若存在，请求出所有符合条件的有序整数对),(k t ；若不存在，请说明理由．【答案】（1）设数列}{n a 的首项为1a ，公差为d ，由已知，有⎩⎨⎧=+=+9333416211d a d a ，……（2分）解得11=a ，2=d ，…………（3分）所以}{n a 的通项公式为12-=n a n （*N ∈n ）．…………（4分）（2）当1=n 时，1111b T b -==，所以211=b ．……（1分）由n n b T -=1，得111++-=n n b T ，两式相减，得11++-=n n n b b b ，故n n b b 211=+，……（2分）所以，}{n b 是首项为21，公比为21的等比数列，所以n n b ⎪⎭⎫ ⎝⎛=21．……（3分） )4(2182191+=+=+m m a m ，…………（4分）要使91+m a 是}{n b 中的项，只要n m 24=+即可，可取4=m ．…………（6分）（只要写出一个m 的值就给分，写出42-=n m ，*N ∈n ，3≥n 也给分）（3）由（1）知，tn n c n +--=1212，…………（1分）要使1c ，2c ，k c 成等差数列，必须k c c c +=122，即tk k t t +--++=+12121136，…………（2分）化简得143-+=t k ．…………（3分）因为k 与t 都是正整数，所以t 只能取2，3，5．…………（4分）当2=t 时，7=k ；当3=t 时，5=k ；当5=t 时，4=k ．…………（5分）综上可知，存在符合条件的正整数t 和k ，所有符合条件的有序整数对),(k t 为： )7,2(，)5,3(，)4,5(．…………（6分）7、等比数列．．．．{}n c 满足11410-+⋅=+n n n c c ，*N n ∈，数列{}n a 满足n a n c 2=（1）求{}n a 的通项公式；（5分）（2）数列{}n b 满足11n n n b a a +=⋅，n T 为数列{}n b 的前n 项和．求n n T ∞→lim ；（5分）（3）是否存在正整数(),1m n m n <<，使得1,,m n T T T 成等比数列？若存在，求出所有,m n 的值；若不存在，请说明理由．（6分）【答案】解：（1）解：40,103221=+=+c c c c ，所以公比4=q 2分 10411=+c c 计算出21=c 3分 121242--=⋅=n n n c 4分 12-=∴n a n 5分（2）11122121n b n n ⎛⎫=- ⎪-+⎝⎭6分于是11111112335212121n n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-= ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎣⎦ 8分 n n T ∞→lim =21 10分（3）假设否存在正整数(),1m n m n <<，使得1,,m n T T T 成等比数列，则2121321m n m n ⎛⎫=⋅ ⎪++⎝⎭， 12分可得2232410m m n m -++=>，由分子为正，解得1122m -<<+由,1m N m *∈>，得2m =，此时12n =，当且仅当2m =，12n =时，1,,m n T T T 成等比数列。

高三上学期考试数学理试题分类汇编：数列Word版含答案

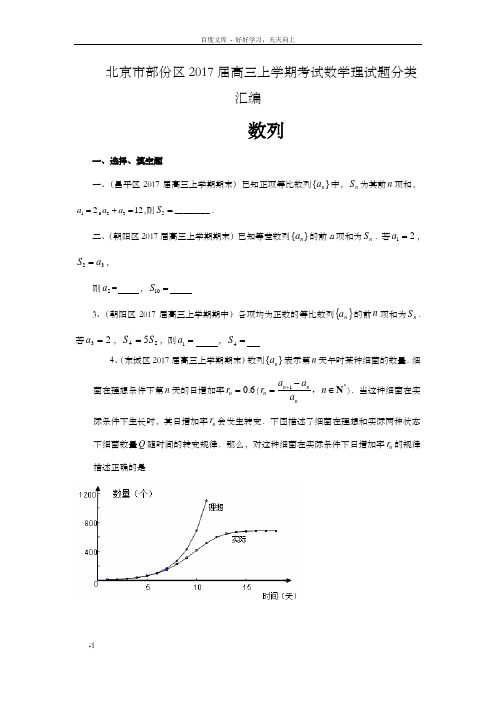
北京市部份区2017届高三上学期考试数学理试题分类汇编数列一、选择、填空题一、（昌平区2017届高三上学期期末）已知正项等比数列{}n a 中，n S 为其前n 项和，12a =,2312a a +=,则5S =________ .二、（朝阳区2017届高三上学期期末）已知等差数列}{n a 的前n 项和为n S ．若12a =，32a S =，则2a = ，10S =3、（朝阳区2017届高三上学期期中）各项均为正数的等比数列{}n a 的前n 项和为n S .若23=a ，245S S =，则1a = ，4S =4、（东城区2017届高三上学期期末）数列{}n a 表示第n 天午时某种细菌的数量．细菌在理想条件下第n 天的日增加率0.6n r =(*1n nn na a r n a +-=∈N ，)．当这种细菌在实际条件下生长时，其日增加率n r 会发生转变．下图描述了细菌在理想和实际两种状态下细菌数量Q 随时间的转变规律．那么，对这种细菌在实际条件下日增加率n r 的规律描述正确的是5、（丰台区2017届高三上学期期末）在等比数列}{n a 中，31=a ，123+=a a a +9，则456+a a a +等于（A ）9（B ）72（C ）9或72（D ） 9或-726、（海淀区2017届高三上学期期中）已知数列{}n a 的前n 项和31n n S =+，则23a a +=_____.7、（石景山区2017届高三上学期期末）等差数列{}n a 学科网中，12a =，公差不为零，且1a ，3a ，11a 恰好是某等比数列的前三项，那么该等比数列公比的值等于．8、（通州区2017届高三上学期期末）设S n 为等差数列{a n }的前n 项和，若11a =，7524S S -=，则6____.S =9、（西城区2017届高三上学期期末）设等比数列{}n a 的各项均为正数，其前n 项和为n S ．若11a =，34a =，则n a =____；6S =____．二、解答题一、（朝阳区2017届高三上学期期末）设(3)m,n m n ≤≤是正整数，数列:m A 12m a ,a ,,a ，其中(1)i a i m ≤≤是集合{123},,,,n 中互不相同的元素．若数列m A 知足：只要存在1i,j i j m ≤<≤（）使i j a a n +≤，总存在1k k m ≤≤（）有i j k a a a +=，则称数列m A 是“好数列”．（Ⅰ）当6100m ,n ==时，（ⅰ）若数列6:11789790A ,,x,y,,是一个“好数列”，试写出x,y 的值，并判断数列：11789097,,,x,,y 是不是是一个“好数列”？（ⅱ）若数列6:1178A ,,a,b,c,d 是“好数列”，且a b c d <<<，求a,b,c,d 共有多少种不同的取值？（Ⅱ）若数列m A 是“好数列”，且m 是偶数，证明：1212m a a a n m ++++≥．二、（朝阳区2017届高三上学期期中）已知数列{}()N n a n *∈是公差不为0的等差数列，11a =，且248111,,a a a 成等比数列. （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设数列11{}n n a a +⋅的前n 项和为n T ，求证:1n T <.3、（朝阳区2017届高三上学期期中）设b a ,是正奇数，数列}{n c （n *∈N ）概念如下：b c a c ==21,，对任意3≥n ，n c 是21--+n n c c 的最大奇约数．数列}{n c 中的所有项组成集合A ．（Ⅰ）若15,9==b a ，写出集合A ；（Ⅱ）对1≥k ，令221=max {,}k k k d c c -(max{,}p q 表示,p q 中的较大值），求证：k k d d ≤+1；（Ⅲ）证明集合A 是有限集，并写出集合A 中的最小数．4、（东城区2017届高三上学期期末）已知{}n a 是等比数列，知足13a =，424a =，数列{}n n a b +是首项为4，公差为1的等差数列．（Ⅰ）求数列{}n a 和{}n b 的通项公式；（Ⅱ）求数列{}n b 的前n 项和．五、（海淀区2017届高三上学期期末）对于无穷数列{}n a ,{}n b ，若1212max{,,,}min{,,,}(1,2,3,)k k k b a a a a a a k =-=，则称{}n b 是{}n a 的“收缩数列”．其中，12max{,,,}k a a a ,12min{,,,}k a a a 别离表示12,,,k a a a 中的最大数和最小数．已知{}n a 为无穷数列，其前n 项和为n S ，数列{}n b 是{}n a 的“收缩数列”． (Ⅰ)若21n a n =+，求{}n b 的前n 项和； (Ⅱ)证明：{}n b 的“收缩数列”仍是{}n b ； (Ⅲ)若121(1)(1)22n n n n n n S S S a b +-+++=+(1,2,3,)n =，求所有知足该条件的{}n a ．六、（丰台区2017届高三上学期期末）已知无穷数列{}n c 知足1112n n c c +=--. （Ⅰ）若117c =，写出数列{}n c 的前4项；（Ⅱ）对于任意101c ≤≤，是不是存在实数M ，使数列{}n c 中的所有项均不大于M ？若存在，求M 的最小值；若不存在，请说明理由；（Ⅲ）当1c 为有理数，且10c ≥时，若数列{}n c 自某项后是周期数列，写出1c 的最大值.（直接写出结果，无需证明）7、（海淀区2017届高三上学期期中）已知数列{}n a 是公差为2的等差数列，数列{}n b 知足1n n n b b a +-=，且2318,24b b =-=-.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）求n b 取得最小值时n 的值.八、（海淀区2017届高三上学期期中）已知数列{}n a 是无穷数列，知足11lg |lg lg |n n n a a a +-=-（2,3,4,n =）.（Ⅰ）若122,3a a ==，求345,,a a a 的值；（Ⅱ）求证：“数列{}n a 中存在*()k a k ∈N 使得lg 0k a =”是“数列{}n a 中有无数多项是1”的充要条件；（Ⅲ）求证：在数列{}n a 中*()k a k ∃∈N ,使得12k a <≤.九、（通州区2017届高三上学期期末）已知数列}{n a 对任意的*N n ∈知足：+212n n n+a a a ，则称数列}{n a 为“T 数列”.（Ⅰ）求证：数列{}2n 是“T 数列”；（Ⅱ）若212nn a n ⎛⎫=⋅ ⎪⎝⎭，试判断数列{}n a 是否是“T 数列”，并说明理由；（Ⅲ）若数列{}n a 是各项均为正的“T 数列”，求证：13212421n na a a n a a a n.10、（西城区2017届高三上学期期末）数字1,2,3,,(2)n n ≥的任意一个排列记作12(,,,)n a a a ，设n S 为所有这样的排列组成的集合．集合12{(,,,)|n n n A a a a S =∈任意整数,,1i j i j n <≤≤，都有}i j a i a j --≤；集合12{(,,,)|n n n B a a a S =∈任意整数,,1i j i j n <≤≤，都有}i j a i a j ++≤．（Ⅰ）用列举法表示集合3A ，3B ；（Ⅱ）求集合nn A B 的元素个数；（Ⅲ）记集合n B 的元素个数为n b ．证明：数列{}n b 是等比数列．参考答案一、选择、填空题一、62 二、4,110 3、12，1524、B 五、D 六、24 7、4 八、36 九、12n -；63二、解答题一、解：（Ⅰ）（ⅰ） 89100x ,y ==，或10089x ,y ==；数列：11789097,,,x,,y 也是一个“好数列”． …………………………………3分（ⅱ）由（ⅰ）可知，数列必含89100,两项，若剩下两项从909199,,,中任取，则都符合条件，有21045C =种；若剩下两项从798088,,,中任取一个，则另一项必对应909199,,,中的一个，有10种；若取6877a ≤≤，则791188a ≤+≤，902299a ≤+≤，“好数列”必超过6项，不符合；若取67a =，则61178a A +=∈，另一项可从909199,,,中任取一个，有10种；若取5667a <<，则671178a <+<，782289a <+<，“好数列”必超过6项，不符合；若取56a =，则67b =，符合条件，若取56a <，则易知“好数列”必超过6项，不符合；综上，a,b,c,d 共有66种不同的取值． ………………………………………7分（Ⅱ）证明：由（Ⅰ）易知，一个“好数列”各项任意排列后，仍是一个“好数列”．又“好数列”12m a ,a ,,a 各项互不相同，所以，不妨设12m a a a <<<．把数列配对：121122m m m m a a ,a a ,,a a -++++，只要证明每一对和数都不小于1n +即可．用反证法，假设存在12mj ≤≤学科网，使1j m j a a n +-+≤，因为数列单调递增，所以111211m j m j m j j m j a a a a a a a n -+-+-+-+<+<+<<+≤，又因为“好数列”，故存在1k m ≤≤，使得1(1)i m j k a a a i j +-+=≤≤，显然1>k m j a a +-，故1k m j >+-，所以k a 只有1j -个不同取值，而1i m j a a +-+有j 个不同取值，矛盾．所以，121122m m m m a a ,a a ,,a a -++++每一对和数都不小于1n +，故12(1)2m ma a a n +++≥+，即1212m a a a n m ++++≥．…………………13分二、解：（Ⅰ）设{}n a 的公差为d ．因为248111,,a a a 成等比数列，所以2428111()a a a =⋅．即2111111()37a d a d a d=⋅+++ ．化简得2111(3)()(7)a d a d a d +=+⋅+，即21d a d =．又11a =，且0d ≠，解得1d = ．所以有1(1)n a a n d n =+-=． …………………7分（Ⅱ）由（Ⅰ）得：11111(1)1n n a a n n n n +==-⋅⋅++．所以11111111122311n T n n n =-+-++-=-<++ ．因此，1n T <． …………………13分 3、解：（Ⅰ）数列}{n c 为：9，15，3，9，3，3，3，……．故集合}3,15,9{=A ． ……………3分（Ⅱ）证明：由题设，对3≥n ，2-n c ，1-n c 都是奇数，所以21--+n n c c 是偶数．从而21--+n n c c 的最大奇约数221--+≤n n n c c c ，所以},m ax {21--≤n n n c c c ，当且仅当21--=n n c c 时等号成立．所以，对1≥k 有k k k k d c c c =≤-+},m ax {12212，且k k k k k k d d d c c c =≤≤++},m ax {},m ax {21222．所以k k k k d c c d ≤=+++},m ax {12221，当且仅当122-=k k c c 时等号成立．………9分（Ⅲ）由（Ⅱ）知，当3≥n 时，有},m ax {21--≤n n n c c c ．所以对3≥n ，有12max max {,}{,}n c c c a b ≤=．又n c 是正奇数，且不超过max {,}a b 的正奇数是有限的，所以数列}{n c 中的不同项是有限的．所以集合A 是有限集．集合A 中的最小数是b a ,的最大公约数． ……………14分4、解：（Ⅰ）设等比数列{}n a 的公比为q ．由题意，得3418a q a ==，2q =．所以11132n n n a a q --==⋅(1,2,)n =． ……………3分又数列{}n n a b +是首项为4，公差为1的等差数列，所以4(1)1n n a b n +=+-⋅．从而1(3)32n n b n -=+-⨯(1,2,)n =． ……………6分（Ⅱ）由（Ⅰ）知1(3)32n n b n -=+-⨯(1,2,)n =数列{3}n +的前n 项和为(7)2n n +． ……………9分数列1{32}n -⋅的前n 项和为3(12)32312n n -=⨯--． ……………12分所以，数列{}n b 的前n 项和为(7)3232n n n +-⨯+． ………13分五、解：（Ⅰ）由21n a n =+可得{}n a 为递增数列，所以12121max{,,,}min{,,,}21322n n n n b a a a a a a a a n n =-=-=+-=-，故{}n b 的前n 项和为22(1)2n n n n -⨯=-.- （Ⅱ）因为12121max{,,,}max{,,,}(1,2,3,)n n a a a a a a n +≤=，12121min{,,,}min{,,,}(1,2,3,)n n a a a a a a n +≥=，所以1211211212max{,,,}min{,,,}max{,,,}min{,,,}n n n n a a a a a a a a a a a a ++-≥-所以1(1,2,3,)n n b b n +≥=. 又因为1110b a a =-=，所以12121max{,,,}min{,,,}n n n n b b b b b b b b b -=-=，所以{}n b 的“收缩数列”仍是{}n b .（Ⅲ）由121(1)(1)22n n n n n n S S S a b +-+++=+(1,2,3,)n =可得当1n =时，11a a =；当2n =时，121223a a a b +=+，即221b a a =-，所以21a a ≥；当3n =时，123133263a a a a b ++=+，即3213132()()b a a a a =-+-（*），若132a a a ≤<，则321b a a =-，所以由（*）可得32a a =，与32a a <矛盾；若312a a a <≤，则323b a a =-，所以由（*）可得32133()a a a a -=-，所以3213a a a a --与同号，这与312a a a <≤矛盾；若32a a ≥，则331b a a =-，由（*）可得32a a =. 猜想：知足121(1)(1)22n n n n n n S S S a b +-+++=+(1,2,3,)n =的数列{}n a 是： 1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩.经验证，左式=121212(1)[12(1)]2n n n S S S na n a na a -+++=++++-=+，右式=112112(1)(1)(1)(1)(1)()22222n n n n n n n n n n n a b a a a na a +-+--+=+-=+.下面证明其它数列都不知足（Ⅲ）的题设条件.法1：由上述3n ≤时的情况可知，3n ≤时，1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩是成立的.假设k a 是第一次不符合1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩的项，则1231k k a a a a a -≤===≠，由题设条件可得2212(1)(1)222k k k k k k k k a a a b ----+=+（*），若12k a a a ≤<，则由（*）式化简可得2k a a =与2k a a <矛盾；若12k a a a <≤，则2k k b a a =-，所以由（*）可得21(1)()2k k k k a a a a --=- 所以21k k a a a a --与同号，这与12k a a a <≤矛盾；所以2k a a ≥，则1k k b a a =-，所以由（*）化简可得2k a a =.这与假设2k a a ≠矛盾.所以不存在数列不知足1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩的{}n a 符合题设条件.法2：当i n ≤时，11212max{,,,}min{,,,}i i i i a a a a a a a a b -≤-=，所以1121()ki k i a a b b b =-≤+++∑，(1,2,3,,)k n =即112()k k S ka b b b ≤++++，(1,2,3,,)k n =由1(1,2,3,)n n b b n +≥=可得(1,2,3,,)k n b b k n ≤=又10b =，所以可得1(1)k n S ka k b ≤+-(1,2,3,)k =，所以12111(2)[02(1)]n n n n n S S S a a na b b b n b +++≤++++⨯++++-，即121(1)(1)22n n n n n nS S S a b +-+++≤+ 所以121(1)(1)22n n n n n n S S S a b +-+++≤+等号成立的条件是1(1,2,3,,)i i n a a b b i n -===，所以，所有知足该条件的数列{}n a 为1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩.（说明：各题的其他做法，可对着参考答案的评分标准相应给分）六、解：（Ⅰ）12462,,,,77777……………….4分（Ⅱ）存在知足题意的实数M , 且M 的最小值为1. 解法一：猜想10≤≤n c ，下面用数学归纳法进行证明. （1）当1n =时,101c ≤≤，结论成立.（2）假设当)(*N k k n ∈=时结论成立，即10≤≤k c ，当1+=k n 时,022k c ≤≤ ,所以1121k c -≤-≤, 即0121k c ≤-≤,所以01121k c ≤--≤, 故01121k c ≤--≤. 又因为+1=112k k c c --, 所以+101k c ≤≤,所以1+=k n 时结论也成立.综上,由（1）,（2）知,10≤≤n c 成立所以1M ≥,当112c =时,可适当2n ≥时, 1n c =,此时, M 的最小值为1 故M 的最小值为1.解法二：当2≥n 时，若存在2,3,4...,k =知足11k c -<,且1k c >. 显然1,21,01≠-k c ，则1211<<-k c 时，1221<-=-k k c c 与1>k c 矛盾； 2101<<-k c 时，121<=-k k c c 与1>k c 矛盾；所以01(2)n c n ≤≤≥ 所以1M ≥,当112c =时,可适当2n ≥时, 1n c =,此时, M 的最小值为1 故M 的最小值为1. ……………………10分（Ⅲ）2………………13分7、解析：（I ）（II ）八、解析：（III）九、解：(Ⅰ)22252n n n ++=⋅，12242n n +⋅=⋅ 212n n n a a a ++∴+-=21222220n n n n +++-⋅=> 212n n n a a a ++∴+>……………….3分(Ⅱ)222112(2)2n n n n a a a n +++⎛⎫+-=+⋅ ⎪⎝⎭212n n ⎛⎫+⋅ ⎪⎝⎭1212(1)2n n +⎛⎫-+⋅ ⎪⎝⎭2221(2)[(1)]24nn n n +⎛⎫=⋅+-+ ⎪⎝⎭214024nn n ⎛⎫-⎛⎫=⋅> ⎪ ⎪⎝⎭⎝⎭解得，*4,n n N >∈，故数列{}n a 不是T 数列.……………….7分(Ⅲ)要证13212421n n a a a n a a a n +++++>+++ 只需证1321242()(1)n n n a a a n a a a ++++>++++……………….8分下面运用数学归纳法证明。

山东省13市2017届高三最新考试数学理试题分类汇编：数列 Word版含答案

山东省13市2017届高三最新考试数学理试题分类汇编数列2017.03一、选择、填空题1、（聊城市2017届高三高考模拟（一））已知数列{}n a 为等差数列，且1251,5,8a a a ≥≤≥，设数列{}n a 的前n 项和为S ，15S 的最大值为M ，最小值为m ，则M m + （） A ．500 B ．600 C. 700 D ．8002、（青岛市2017年高三统一质量检测）已知1x >，1y >，且lg x ，14，lg y 成等比数列，则xy 有A ．最小值10 BC ．最大值10D二、解答题QQ 请到学科网下载，不要放到群1、（滨州市2017届高三下学期一模考试）已知数列{}n a 满足22,,2,n n n a n a n N a n +++⎧⎪=∈⎨⎪⎩为奇数为偶数，且121,2a a ==.（1）求数列{}n a 的通项公式；（2）令1(1),n n n n b a a n N ++=-∈，求数列{}n b 的前n 项和n S .2、（德州市2017届高三第一次模拟考试）已知数列{}n a 与{}n b 满足112()n n n n a a b b ++-=-，n N +∈，21n b n =-，且12a =．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设1nn n n na cb -=，n T 为数列{}nc 的前n 项和，求n T ．3、（菏泽市2017年高考一模）在数列{a n }中，a 1=1，=+（n ∈N*）．（1）求数列{a n }的通项公式；（2）设b n =1+a（n ∈N*），求数列{2nb n }的前n 项和S n ．4、（济宁市2017届高三第一次模拟（3月））已知数列{}n a 的前n 项和为n S ，且满足()22n n S a n N *=-∈，数列{}n b 为等差数列，且满足2183,b a b a ==．(I)求数列{}n a ，{}n b 的通项公式； (II)令()111n n n c a +=--，关于k 的不等式()40971100,k c k k N *≥≤≤∈的解集为M ，求所有()k k a b k M +∈的和S ．5、（聊城市2017届高三高考模拟（一））设,n n S T 分别是数列{}n a 和{}n b 的前n 项和，已知对于任意*n N ∈，都有323n n a S =+，数列{}n b 是等差数列，且51025,19T b ==. （Ⅰ）求数列{}n a 和{}n b 的通项公式；（Ⅱ）设()1n nn a b c n n =+，数列{}n c 的前n 项和为R ，求使n R >2017成立的n 的取值范围.6、（临沂市2017届高三2月份教学质量检测（一模））已知数列{}n a 的前n 项和为n S ，且()21n n S a n n N *=+-∈．(I)求数列{}n a 的通项公式；(II)定义[]x x x =+，其中[]x 为实数x 的整数部分，x 为x 的小数部分，且01x ≤<，记1n n n na a c S +=，求数列{}n c 的前n 项和n T ．7、（青岛市2017年高三统一质量检测）已知数列{}n a 的前n 项和为n S ,11a =,且121n n a S +=+,N n *∈.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）令32log n n c a =，21n n n b c c +=⋅ ，记数列{}n b 的前n 项和为n T ，若对任意N n *∈，n T λ<恒成立，求实数λ的取值范围.8、（日照市2017届高三下学期第一次模拟）已知数列{}n a 满足1111,14n na a a +==-，其中n N +∈.(I)设221n n b a =-，求证：数列{}n b 是等差数列，并求出数列{}n a 的通项公式；(II)设41n n a c n =+，数列{}2n n c c +的前n 项和为n T ，是否存在正整数m ，使得11n m m T c c +<对于n N +∈恒成立，若存在，求出m 的最小值，若不存在，请说明理由．9、（泰安市2017届高三第一轮复习质量检测（一模））若数列{}n a 是公差为2的等差数列，数列{}n b 满足1211,2n n n n b b a b b nb +==+=且 (I)求数列{}{}n n a b 、的通项公式； (Ⅱ)设数列{}n c 满足11n n n a c b ++=，数列{}n c 的前n 项和为n T ，若不等式()1nn T λ-<12n n -+对一切n N *∈都成立，求实数λ的取值范围.10、（潍坊市2017届高三下学期第一次模拟）已知数列{}n a 是等差数列，其前n 项和为n S 。

2017年数列汇编 - 答案

金牌数学高二（必修五）专题系列之数列（四）2107年真题汇编一、等差数列1．通项公式： . 2．等差中项： . 3．求和公式： . 4．性质： . 二、等比数列1.通项公式： .2.等比中项： .3.求和公式： .4.性质： .三、等差等比通用公式： .题型一选择题例1： (2017年新课标Ⅰ) 4．记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为 A ．1B ．2C ．4D ．8【答案】C【解析】设公差为d ，则有112724,61548a d a d +=⎧⎨+=⎩解得4d =，故选 C.变式训练1. ( 2017年新课标Ⅱ卷理) 3.我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（）A ．1盏B ．3盏C ．5盏D ．9盏【答案】B【解析】塔的顶层共有灯x 盏，则各层的灯数构成一个公比为2的等比数列，由()71238112x -=-可得3x =，故选B 。

2. (2017年新课标Ⅲ卷理) 9．等差数列{}n a 的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为 A ．-24 B ．-3 C ．3 D ．8【答案】A【解析】设等差数列的公差为0d ≠，()()()2232612115a a a d d d =⋅⇒+=++，22d d =-，()0d ≠，所以2d =-，()665612242S ⨯=⨯+⨯-=-，故选A. 3. (2017年浙江卷) 6．已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d >0”是“S 4 + S 6>2S 5”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C题型二填空题例2：( 2017年新课标Ⅱ卷理) 15.等差数列{}n a 的前n 项和为n S ，33a =，410S =，则11nk kS==∑ ．【答案】21nn + 【解析】设等差数列的首项为1a ，公差为d ，所以1123434102a d a d +=⎧⎪⎨⨯+=⎪⎩ ，解得111a d =⎧⎨=⎩ ，所以()1,2n nn n a n S +==，那么()1211211n S n n n n ⎛⎫==- ⎪++⎝⎭，那么11111111221......21223111nk k n S n n n n =⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦∑ .变式训练1.(2017年新课标Ⅲ卷理)设等比数列{}n a 满足a 1 + a 2 = –1, a 1 – a 3 = –3，则a 4 = ___________．【答案】8-【解析】由题意可得：()()1211113a q a q ⎧+=-⎪⎨-=-⎪⎩ ，解得：112a q =⎧⎨=-⎩ ，则3418a a q ==-2. (2017年北京卷理) （10）若等差数列{}n a 和等比数列{}n b 满足a 1=b 1=–1，a 4=b 4=8，则22a b =_______. 【答案】1【解析】322131383,211(2)a d q d qb -+-+=-=⇒==-⇒==-⨯-3. (2017年江苏卷)等比数列{}n a 的各项均为实数，其前n 项和为n S ，已知3676344S S ==,，则8a = ▲ ．【解析】当1q =时，显然不符合题意；当1q ≠时，3161(1)714(1)6314a q q a q q⎧-=⎪-⎪⎨-⎪=⎪-⎩，解得1142a q ⎧=⎪⎨⎪=⎩，则7812324a =⨯=.题型二解答题例3：( 2017年全国Ⅲ卷文)设数列{}n a 满足()123+212n a a n a n ++-=… （1）求数列{}n a 的通项公式；（2）求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和；【答案】【解析】（1）当=1n 时，12a = (1)当2n ≥时，由()123+212n a a n a n ++-=...① (2)()()12-13+232-1n a a n a n ++-=...②. (3)① -②得()212n n a -= (4)即()2221n a n n =≥- 验证12a =符合上式所以()221n a n N n *=∈- (6)（2）()()2112121212121n a n n n n n ==-+-+-+ (8)11111111211335232121212121n nS n n n n n n =-+-++-+-=-=---+++ (12)变式训练1.(2017年天津卷理)已知{}n a 为等差数列，前n 项和为()n S n *∈N ，{}n b 是学科.网首项为2的等比数列，且公比大于0，2312b b +=,3412b a a =-，11411S b =.（Ⅰ）求{}n a 和{}n b 的通项公式；（Ⅱ）求数列221{}n n a b -的前n 项和()n *∈N .【答案】（1）32n a n =-.2nn b =.（2）1328433n n n T +-=⨯+. 【解析】（I ）设等差数列{}n a 的公差为d ，等比数列{}n b 的公比为q .由262n a n =-，12124n n b --=⨯，有221(31)4nn n a b n -=-⨯，故23245484(31)4n n T n =⨯+⨯+⨯++-⨯，23414245484(34)4(31)4n n n T n n +=⨯+⨯+⨯++-⨯+-⨯，上述两式相减，得231324343434(31)4n n n T n +-=⨯+⨯+⨯++⨯--⨯1112(14)4(31)414(32)48.n n n n n ++⨯-=---⨯-=--⨯- 得1328433n n n T +-=⨯+. 所以，数列221{}n n a b -的前n 项和为1328433n n +-⨯+. 2【山东省济南市2012届高三12月考】28. （本小题满分8分）已知}{n a 是一个公差大于0的等差数列，且满足16,557263=+=a a a a . (Ⅰ)求数列}{n a 的通项公式：（Ⅱ）等比数列}{n b 满足：1,2211-==a b a b ，若数列n n n b a c ⋅=，求数列}{n c 的前n 项和n S .【答案】28．（本小题满分8分）解：(Ⅰ)设等差数列{}n a 的公差为d ，则依题设d >0 由1672=+a a .得12716a d += ① ---------------1分由3655,a a ⋅=得11(2)(5)55a d a d ++= ② ---------------2分由①得12167a d =-将其代入②得(163)(163)220d d -+=。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017届高三复习：数列大题训练50题1 ．数列{n a }的前n 项和为n S ，且满足11a =，2(1)n n S n a =+. （1）求{n a }的通项公式；（2）求和T n =1211123(1)na a n a ++++.2 ．已知数列}{n a ，a 1=1，点*))(2,(1N n a a P n n ∈+在直线0121=+-y x 上. （1）求数列}{n a 的通项公式；（2）函数)2*,(1111)(321≥∈++++++++=n N n a n a n a n a n n f n且，求函数)(n f 最小值.3 ．已知函数x ab x f =)( (a ，b 为常数)的图象经过点P （1，81）和Q （4，8）(1) 求函数)(x f 的解析式；(2) 记a n =log 2)(n f ,n 是正整数，n S 是数列{a n }的前n 项和，求n S 的最小值。

4 ．已知y ＝f (x )为一次函数，且f (2)、f (5)、f (4)成等比数列，f (8)＝15．求n S ＝f (1)＋f (2)＋…＋f (n )的表达式． 5 ．设数列{}n a 的前n 项和为n S ，且1n n S c ca =+-，其中c 是不等于1-和0的实常数.（1）求证: {}n a 为等比数列；（2）设数列{}n a 的公比()q f c =，数列{}n b 满足()()111,,23n n b b f b n N n -==∈≥，试写出1n b⎧⎫⎨⎬⎩⎭的通项公式，并求12231n n b b b b b b -+++的结果.6 ．在平面直角坐标系中,已知A n (n,a n )、B n (n,b n )、C n (n -1,0)(n ∈N*)，满足向量1+n n A A 与向量n n C B 共线，且点B n (n,b n ) (n ∈N*)都在斜率为6的同一条直线上.(1)试用a 1,b 1与n 来表示a n ;(2)设a 1=a ,b 1=-a ,且12<a ≤15，求数列{a n }中的最小项.7 ．已知数列{}n a 的前三项与数列{}n b 的前三项对应相同，且212322a a a +++…12n n a -+8n =对任意的∈n N*都成立，数列1{}n n b b +-是等差数列．（1）求数列{}n a 与{}n b 的通项公式；（2）问是否存在k ∈N *，使得(0,1)k k b a -∈请说明理由． 8 ．已知数列),3,2(1335,}{11 =-+==-n a a a a n n n n 且中（I ）试求a 2，a 3的值；（II ）若存在实数}3{,nn a λλ+使得为等差数列，试求λ的值. 9 ．已知数列{}n a 的前n 项和为n S ，若()1,211++=⋅=+n n S a n a n n ，（1）求数列{}n a 的通项公式; （2）令n nn S T 2=，①当n 为何正整数值时，1+>n n T T ：②若对一切正整数n ，总有m T n ≤，求m 的取值范围。

10．已知数列}{n a 的前n 项和)(n f 是n 的二次函数，)(n f 满足),2()2(n f n f -=+且.3)1(,0)4(-==f f（1）求数列}{n a 的通项公式；（2）设数列}{n b 满足21++=n n n a a b ，求}{n b 中数值最大和最小的项. 12．已知数列{}n a 中，12a =，且当2n ≥时，1220n n n a a ---= （1）求数列{}n a 的通项公式；（2）若{}n a 的前n 项和为n S ，求n S 。

13．正数数列{}n a 的前n 项和n S，满足1n a =+，试求：（I ）数列{}n a 的通项公式；（II ）设11n n n b a a +=，数列的前n 项的和为n B ，求证：12n B <。

14．已知函数)(x f =157++x x ,数列{}n a 中,2a n +1－2a n +a n +1a n =0，a 1=1,且a n ≠0, 数列{b n }中, b n =f (a n －1) （1）求证：数列{na 1}是等差数列；（2）求数列{b n }的通项公式； (3)求数列{n b }的前n 项和S n .15．已知函数)(x f ＝a ·b x 的图象过点A （4，41）和B （5，1）．（1）求函数)(x f 解析式；（2）记a n ＝log 2)(n f n ∈N *，n S 是数列{}n a 的前n 项和，解关于n 的不等式0≤⋅n n S a16．已知数列{}n a 的前n 项的和为n S ，且()0,21≠≥⋅=-n n n n S n S S a ，921=a . （1）求证：⎭⎬⎫⎩⎨⎧n S 1为等差数列；（2）求数列{}n a 的通项公式．17．在平面直角坐标系中，已知),(n n a n A 、),(n n b n B 、*))(0,1(N n n C n ∈-，满足向量1n n A A +与向量n n C B 共线，且点),(n n b n B *)(N n ∈都在斜率6的同一条直线上. （1）证明数列{}n b 是等差数列；（2）试用11,b a 与n 来表示n a ；（3）设a b a a -==11,，且1215≤<a ，求数}{n a 中的最小值的项. 18．设正数数列{n a }的前n 项和n S 满足2)1(41+=n n a S ．（I ）求数列{n a }的通项公式；（II ）设11+⋅=n n n a a b ，求数列{n b }的前n 项和n T ．19．已知等差数列{a n }中，a 1=1,公差d >0，且a 2、a 5、a 14分别是等比数列{b n }的第二项、第三项、第四项. (Ⅰ)求数列{a n }、{b n }的通项a n 、b n ; (Ⅱ)设数列{c n }对任意的n ∈N*，均有2211b c b c ++…＋nn b c ＝a n+1成立，求c 1+c 2+…+c 2005的值.20．已知数列{n a }满足11=a ，且),2(22*1N n n a a n n n ∈≥+=-且（1）求证：数列{n na 2}是等差数列；（2）求数列{n a }的通项公式；（3）设数列{n a }的前n 项之和n S ，求证：322->n S nn。

21．设数列{a n }的前n 项和为n S =2n 2，{b n }为等比数列，且a 1=b 1，b 2(a 2 －a 1) =b 1。

（1）求数列{a n }和{b n }的通项公式；（2）设c n =nnb a , 求数列{c n }的前n 项和T n .22．已知函数()f x与函数y =(a ＞0)的图象关于x y =对称. (1) 求()f x ;(2)若无穷数列{}n a 满足1121,n n a S a a a ==++⋅⋅⋅+,且点)n n P S 均在函数()y f x =上,求a 的值,并求数列1n a ⎧⎫⎨⎬⎩⎭的所有项的和(即前n 项和的极限)。

23．已知函数))((,1}{,13)(11*+∈==+=N n a f a a a x xx f n n n 满足数列（1）求证：数列}1{na 是等差数列；（2）若数列}{nb 的前n 项和.,,122211n nn n n n T a b a b a b T S 求记+++=-= 24．已知数列{}n a 和{}n b 满足：11a =，22a =，0n a >，n b =*n ∈N ），且{}n b 是以q 为公比的等比数列（I ）证明：22n n a a q +=；（II ）若2122n n n c a a -=+，证明数列{}n c 是等比数列；（III ）求和：1234212111111n na a a a a a -++++++ 25．已知a 1=2，点(a n ,a n +1)在函数f (x )=x 2+2x 的图象上，其中n=1，2，3，… （1）证明数列｛lg(1+a n )｝是等比数列；（2）设T n =(1+a 1) (1+a 2) …(1+a n )，求数列｛a n ｝的通项及T n ；26．等差数列}{n a 是递增数列，前n 项和为n S ，且a 1，a 3，a 9成等比数列，255a S =．(1)求数列}{n a 的通项公式；(2)若数列}{n b 满足121+⋅++=n n n a a n n b ，求数列}{n b 的前n 项的和．27．已知向量11(2,),(,2),()n n n n a a b a n N ++==∈*且11a =.若a 与b 共线, （1）求数列{}n a 的通项公式；（2）求数列{}n a 的前n 项和n S .28．已知：数列}{n a 满足+-∈=++++N a n a a a a n n ,333313221 . （1）求数列}{n a 的通项；（2）设,nn a nb =求数列}{n b 的前n 项和S n .29．对负整数a ，数310,66,32++++a a a a 可构成等差数列. （1）求a 的值；（2）若数列{}n a 满足)(211+++∈-=N n a a a n n n 首项为0a ，①令nn n a b )2(-=，求{}n b 的通项公式；②若对任意1212-+<+∈n n a a N n 有，求0a 取值范围. 30．数列.23,5,2}{1221n n n n a a a a a a -===++满足（1）求证：数列}{1n n a a -+是等比数列；（2）求数列{n a }的通项公式；（3）若.}{,n n n n S n b na b 项和的前求数列=31．已知二次函数()y f x =的图像经过坐标原点，其导函数为'()62f x x =-，数列{}n a 的前n 项和为n S ，点(,)()n n S n N *∈均在函数()y f x =的图像上。

（Ⅰ）、求数列{}n a 的通项公式；（Ⅱ）、设13+=n n n a a b ，n T 是数列{}n b 的前n 项和，求使得20n mT <对所有n N *∈都成立的最小正整数m ；32．已知数列{a n }的前n 项和为S n ，且满足)2(02,2111≥=+=-n S S a a n n n（Ⅰ）判断}1{nS 是否为等差数列？并证明你的结论；（Ⅱ）求S n 和a n（Ⅲ）求证：.4121....22221nS S S n -≤+++ 33．若n A 和n B 分别表示数列{}n a 和{}n b 的前n 项和，对任意正整数n 有n A B n a n n n 13124,232=-+-=。