中考数学专题隐圆中最值问题
中考数学善用隐形圆、巧解最值题

中考数学善⽤隐形圆、巧解最值题
近年来,⼏何中因动点⽽产⽣线段最值问题⼴泛出现,成为中考的热点和难点。
此类题型⼀般都会以选择或填空的压轴形式出现,其中⼜以构造“隐形圆”来解决最值问题,条件隐藏较深,学⽣难以把握哪些题型需要构造“隐形圆”处理。
今天笔者想通过本篇⽂章与⼤家分享构造“隐形圆”的常见题型,以便学⽣掌握出题者的套路,灵活运⽤“隐形圆”解题。
【知识储备】
最值问题的解决⽅法通常有两⼤类:
(1)应⽤⼏何性质:
①三⾓形的三边关系:两边之和⼤于第三边,两边之差⼩于第三边;
②两点间线段最短;
③连结直线外⼀点和直线上各点的所有线段中,垂线段最短;
④定圆中的所有弦中,直径最长。
(2)运⽤代数证法:
①运⽤配⽅法求⼆次三项式的最值;
②运⽤⼀元⼆次⽅程根的判别式。
动态图在此!⼀⽬了然!
动态图在此!⼀⽬了然!
写在最后:⼏何中的动态题是难点也是重点,很多时候我们要抓住问题的不变量,并对不变量进⾏追问。
⼀招长江三叠浪:定点是谁?定长(⾓)有吗?轨迹如何?
最值问题就会信⼿拈来!。
专题18 隐形圆及最值问题

AB是 O 的直径,
ACB 90.
ABC 45 , AC 5 ,
ABC 45 ,
AB AC 5 5 2 , sin 45 2 2
MN最大
52 2
.
故答案为: 5 2 .
6.如图,在平面直角坐标系中,已知 C(3, 4) ,以点 C 为圆心的圆与 y 轴相切.点 A 、 B 在 x 轴上,且 OA OB .点 P 为 C 上的动点, APB 90 ,则 AB 长度的最大值为 .
1.如图,等边 ABC 的边长为 2, A 的半径为 1,D 是 BC 上的动点,DE 与 A 相切于 E , DE 的最小值是 ( )
A.1
B. 2
C. 3
D.2
【分析】连接 AE , AD ,作 AH BC 于 H ,因为 DE 与 A 相切于 E ,所以 AE DE , 可得 DE AD2 AE2 AD2 1 ,当 D 与 H 重合时, AD 最小,此时 DE 最小,求出 AH 的长,即可得出 DE 的最小值. 【解答】解:如图,连接 AE , AD ,作 AH BC 于 H ,
若平面上 A、B、C、D 四个点满足 ABC ADC , 则 A、B、C、D 四点共圆. 证明条件:1.四边形对角互补; 2.四边形外角等于内对角.
两条线段被一点分成(内分或外分)两段长的乘积相等,则这两条线段的四个端点共圆.
D
C
H
O
A
B
四边形 ABCD 的对角线 AC、BD 交于 H, 若 AH CH BH DH ,则 A、B、C、D 四点共圆.
作 AM⊥BP 于 M.当点 P 从点 C 运动到点 A 时,线段 BM 的中点 N 运动的路径长为(
)
A. 2 π 2
2023年中考数学一轮复习专题利用隐形圆求圆的最值课件

8
方法总结:利用隐圆解决线圆最值问题时, 第一:变化中寻找不变,找到隐圆; 第二:“一线穿心”--过圆心向定线段作垂直 找到圆上目标最值点,求得最值。
坚持用每一天的进步书写人生的辉煌
9
变式训练2:如图,在矩形ABCD中,AB=3,BC=4, O为矩形ABCD的中心,以D为圆心,1为半径作⊙D, P为⊙D上的一个动点,连接AP、OP、AO,则△AOP 面积的最大,延长AO至C点,过点D作 DF⊥AC于点F,延长FD交⊙D于点P′, 连接AP′,OP′,要使△AOP面积最大, 则只需AO边上的高最大,此时P′满足条 件,即P′F为最大的高,
坚持用每一天的进步书写人生的辉煌
11
拓展:定弦定角型
如图1⊙O中,A、B为定点,则AB为定弦,点C为优弧上 任一点,在C点运动过程中则∠ACB的度数不变⇒逆运用⇒ 如图2、点A、B为定点,点C为线段AB外一点,且 ∠ACB=θ(θ为固定值)⇒点C在以AB为弦的圆上运动( 不与A、B重合)
是_______.
D
C
M A
AN
B
坚持用每一天的进步书写人生的辉煌
方法总结:利用隐圆解决点圆最值问题时, 第一:变化中寻找不变,找到隐圆; 第二:“一线穿心”--连接圆心和定点找到 圆上目标最值点,求得最值。
坚持用每一天的进步书写人生的辉煌
6
变式训练1: 如图,在Rt△ABC中,∠ABC=90°, ∠C=30°,AB=1,点D在AC边上运动,点E为AC的 中点,将△BCD沿BD翻折,点C的对应点为点F,则 在点D从C到A的运动过程中,线段EF的最小值为___.
1
上的一点,且AM= AD,N是AB边上3 的一动点,将△AMN沿MN
所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值
2020年九年级数学中考专题复习:隐形圆求最值问题(含答案)
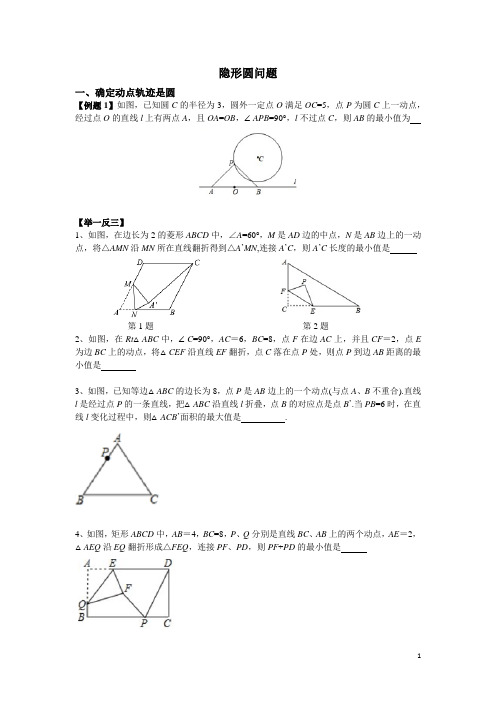
隐形圆问题一、确定动点轨迹是圆【例题1】如图,已知圆C的半径为3,圆外一定点O满足OC=5,点P为圆C上一动点,经过点O的直线l上有两点A,且OA=OB,∠APB=90°,l不过点C,则AB的最小值为【举一反三】1、如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A’MN,连接A’C,则A’C长度的最小值是第1题第2题2、如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E 为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是3、如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.当PB=6时,在直线l变化过程中,则△ACB’面积的最大值是.4、如图,矩形ABCD中,AB=4,BC=8,P、Q分別是直线BC、AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF、PD,则PF+PD的最小值是二、定边对直角知识回顾:直径所对的圆周角是直角构造思路:一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.图形释义:若AB是一条定线段,且∠APB-90°,则P点轨迹是以AB为直径的圆【例题1】已知正方形ABCD边长为2,E、F分别是BC、CD上的动点,且满足BE=CF,连接AE、BF,交点为P点,则PC的最小值为【举一反三】1、如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF,连接CF交BD于点G,连接BE交AG于点H,若正方形边长为2,则线段DH长度的最小值是2、如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠P AB =∠PBC,则线段CP长的最小值是3、如图,AB是半圆O的直径,点C在半圆O上,AB=5,AC=4.D是弧BC上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为4、如图,在Rt△ABC中,∠BAC=90°,AC=12,AB=10,点D是AC上的一个动点,以AD为直径作圆O,连接BD交圆O于点E,则AE的最小值为5、如图,正方形ABCD的边长为4,动点E、F分別从点A、C同时出发,以相同的速度分别沿AB、CD向终点B、D移动,当点E到达点B时,运动停止,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为【辅助圆+将军饮马】如图,正方形ABCD的边长是4,点E是AD边上一动点,连接BE,过点A作AF⊥BE于点F,点P是AD边上另一动点,则PC+PF的最小值为【辅助圆+相切】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=4,D是BC上一动点,CE⊥AD于E,EF⊥AB交BC于点F,则CF的最大值是三、定边对定角在“定边对直角”问题中,依据“直径所对的圆周角是直角”,关键性在于寻找定边、直角,而根据圆周角定理:同圆或等圆中,同弧或等弧所対的圆周角都相.定边必不可少,而直角则可一般为定角.例如,AB为定值,∠P为定角,则P点轨迹是一个圆.当然,∠P度数也是特殊角,比如30°、45°、60°、120°,下面分别作对应的轨迹圆若∠P=30°,以AB为边,同侧构造等边三角形AOB,O即为圆心若∠P=45°,以AB为斜边,同侧构造等腰直角三角形AOB,O即为圆心.若∠P=60°,以AB为底,同侧构造顶角为120°的等腰三角形AOB,O即为圆心.若∠P=120°,以AB为底,异侧为边构造顶角为120°的等腰三角形AOB,O即为圆心.【例题1】如图,等边△ABC边长为2,E、F分別是BC、CA上两个动点,且BE=CF,连接AE、BF,交点为P点,则CP的最小值为【举一反三】1、如图,△ABC为等边三角形,AB=3,若P为△ABC内一动点,且满足∠P AB=∠ACP,则线段PB长度的最小值为2、在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是3、如图,AB是圆O的直径,M、N是弧AB(异于A、B)上两点,C是弧MN上一动点,∠ACB 的角平分线交圆O于点D,∠BAC的平分线交CD于点E,当点C从点M运动到点N时,则C、E两点的运动路径长的比是。
隐形圆最值问题初中题型

隐形圆最值问题初中题型
隐形圆最值问题是初中数学中的一个常见题型,也是一个优化问题。
该问题通常涉及到一个平面内的几何图形,并要求根据给定条件找到某个属性的最大值或最小值。
以下是一个典型的隐形圆最值问题:
问题:已知一个正方形的周长为20cm。
在正方形内部有一个圆,使得圆与正方形的边界相切。
求这个圆的最大半径。
解答:设正方形的边长为a,圆的半径为r。
根据条件,圆与正方形的边界相切,表示圆正好与正方形的边界接触,没有超出正方形。
根据正方形的周长为20cm可知: 4a = 20 a = 5cm
设圆的半径为r,圆的直径为2r。
由于圆与正方形的边界相切,所以圆的直径等于正方形的边长,即2r = a。
代入已知条件可得: 2r = a 2r = 5
解出r得最大半径: r = 5/2 r = 2.5cm
因此,该正方形内的隐形圆的最大半径为2.5cm。
在解决类似的隐形圆最值问题时,关键是将问题进行合理的建模和分析。
通过设定适当的变量和条件,利用等式或不等式关系,可以得到最终的结果。
重要的是将问题化归为数学计算的形式,然后进行推导和求解。
隐形圆最值问题需要仔细观察和分析,巧妙运用数学知识和方法,才能得到准确的最值结果。
中考数学复习 寻找隐圆,求解最值

隐隐圆圆条条件件:: OA∠ABDO==B2=O(定1C线3=5)°5(定为角定)值
发现模型 —— 模型三 四点共圆
例3 如图 ,等边△ABC 中,AB =6,P 为 AB 上一动点, 若∠AEP +∠BDP= 180°,求DE 的最小值.
(3)求在旋转过程中点P的纵坐标的最大值
P
P P P
1、基本模型:
课堂小结
PAmin PA1
PAmax PA2
当PA与⊙O相切时, ∠APO最大
一定一动点,动点在圆上
2、注意挖掘隐圆的条件
模型一 定点定长定圆 模型二 定线定角定圆 模型三 四点共圆
走进中考(课后作业)
在边长为4的菱形ABCD中,∠A=60°,M是AD边上的中点,N
OM=2(定线) ∠ADM=90°(定角)
• 隐圆模型二 定线定角定圆
在圆O中,若AB为直 径,则∠ACB=90°
若AB是固定的线段,且总 有∠ACB=90°, 则C在以AB为直径的圆上.
• 隐圆模型二 定线定角定圆
在圆O中,若弦AB长度固定, 则弦AB(同侧)所对的圆周角相等.
若有一固定线段AB及AB 所对的∠C角度不变, 则C在以AB为弦的圆上.
易证△ABE≌△DCF △DAG≌△DCG
隐圆条件:∠AHB=90°
挑战自我
A(4,0)、B(0,2),点F为AB上一点且AF=2, 将线段AF绕点A旋转,在旋转过程中,点P始终为 BF中点,求线段OP的最大值
发现模型 —— 隐圆模型一 定点定长定圆
例1 如图,在△ABC 中,∠ACB=90°,∠ABC=30°,将 △ABC 绕顶点C 顺时针旋转,得到△MNC,P、Q 分别是 AC、MN 的中点,AC=2,连结PQ,求旋转时PQ 的最
中考数学专题《隐形圆解析》

D
E O
C
B
取 CB 中点 M,所以 E 点轨迹是以 M 为圆心、CB 为直径的圆弧.
A
D
E O
CM
B
连接 AM,与圆弧交点即为所求 E 点,此时 AE 值最小, AE AM EM 102 22 2 2 26 2 .
A
E
C
M
B
【2019 园区一模】如图,正方形 ABCD 的边长为 4,动点 E、F 分别从点 A、C 同时出发,
C
M
E
A
O
B
【寻找定边与直角】如图,在 Rt△ABC 中,∠ACB =90°,BC=4,AC=10,点 D 是 AC 上的 一个动点,以 CD 为直径作圆 O,连接 BD 交圆 O 于点 E,则 AE 的最小值为_________.
A
D
O
E
C
B
【分析】连接 CE ,由于 CD 为直径,故∠CED=90°,考虑到 CD 是动线段,故可以将此 题看成定线段 CB 对直角∠CEB .
A
D
O
P
F
B
E
C
连接 OC,与圆的交点即为 P 点,再通过勾股定理即可求出 PC 长度. 思路概述:分析动点形 成原理,通常“ 非直即圆” (不是直线就 是圆),接下来可以 寻找与动 点相关有无定直线与定 角.
【2013 武汉中考】如图,E 、F 是正方形 ABCD 的边 AD 上的两个动点,满足 AE =DF,连 接 CF 交 BD 于点 G,连接 BE 交 AG 于点 H,若正方形边长为 2,则线段 DH 长度的最小 值是________.
A
O
B
【辅助圆+相切】如图,在 Rt△ABC 中,∠ACB =90°,∠B=30°,AB =4,D 是 BC 上一动点, CE ⊥AD 于 E ,EF⊥AB 交 BC 于点 F,则 CF 的最大值是_________.
2024专题4.2圆---利用“隐圆”模型求最值-中考数学二轮复习必会几何模型剖析(全国通用)

2.如图,在矩形ABCD中,AB=4,AD=6,点E是AB边上的中点,点F是线段BC边上
的动点,将△EBF沿EF所在直线折叠得到△EB´F,连接B´C,则B´C最小值是
A
2 10-2
________.
A
B
O
C
D
B´
E
B´
B
F
C
模型分析
线圆最值---心垂线
考点4-2
典型例题
点圆最值---点心线
考点4-1
【例1】有一架靠在直角墙面的梯子(MN=4)正在下滑,D点出有一只猫紧紧
盯住位于梯子MN的正中间E处的老鼠,等待与老鼠距离最小时扑捉.把墙面,
梯子,猫和老鼠看成同一平面内的线或点,点D到BA,BC的距离分别为4和2.
2 5-2
猫与老鼠的距离DE的最小值为_______.
∴BC=2BE≥ 1+cosα
∴BE=r·sinα≥
1+cosα
C
B
E
2
D
h ·sinα
∴S△ABCmin= 1+cosα
典例精讲
定角夹定高
考点4-4
【例3-1】如图,在△ABC中,∠BAC=60º,BC边上的高AD为3 ,则BC的最小
6
值为___.
解:作△ABC的外接圆,连接OA,OB,OC,
∴∠ADC=135º为定角,AC为定边.
∴∠AGC=90º,
∵AB=6,∴ AC = 3
D
2
,∴AG=CG=3.
BG 3 5 , BDm in 3 5 3
A
O
B
强化训练
与“圆”有关的最值问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何求最值是初中数学难点之一,而“隐圆”问题便是常见的一类考题,此类问题综合性强 (常常会牵扯到三角形、四边形、甚至坐标系等问题),隐蔽性强(不容易想到),加上部分题 目的计算量很大,很容易造成同学们的丢分。近年来在全国各地的中考或名校的模拟考试中经常 会出现“隐圆”求最值的问题(2014、2015、2016连续三年陕西中考的压轴题的最后一问都牵 扯到了隐圆)。此类题目出现的位置一般是在填空的最后一题或是压轴题,基本都是难题。广大 学生在此问题上经常丢分,甚至已经到了谈“隐圆”变色的地步。
A
P BD
P'
E
C
方法总结
名师说法
附:圆外一点到圆上的最小距离和最大距离 如图:点 P 为圆O 外一点,连接 PO 交圆O 于M 点,延长 PO 交圆O 于 N 点。 则线段 PM 长为点 P 到圆O 上一点的最小距离;线段 PN 长为点 P 到圆O 上一点的最大距离
P
O
N
M
名师数学
温馨提示:
在动点运动的过程中同学们要注意的是:虽然点在动(或不确定位置), 但题目一定会有一些量是不变的,可能是某条线段的长度不变,也可能是 某个角度不变,也有可能某个线与线、线与角、角与角的关系不变,这样 才能化动态问题为定态问题。这个需要同学们对题目进行认真的分析和B = 900 ,AB = 6 ,BC = 8 ,D 为 AC 边一动点,过点 D 作DE ⊥DF
,分别交 AB 边、 BC 边于 E 、 F 两点,则 EF 的最小值是
。
A
E
D
B
F
C
思路)分析:
由于在四边形 EBFD 中 ,DE ⊥ DF ,∠B = 90o ,所以 E、B、F、D 四点共圆(对角互补的四边形 四个顶点共圆),且 EF 为圆的直径(如图 2)。所以,要求 EF 的最小值其实质就是求圆的直 径最小值。
D C
M
A
B
P
O
秘籍三:
知识原型:利用“定线(弦)定角存隐圆”求最值
例 3:边长为 3 的等边ΔABC , D 、 E 分别为边 BC 、 AC 上的点,且 BD = CE , AD 、BE
交于P 点,则CP 的最小值为
。
A
E P
BD
C
思路)分析:
分 析 : 由 题 目 条 件 可 知 Δ A B D ≌ΔBCE ,所以∠BAD = ∠CBE , 又 因 为 ∠ C B E +∠ABE = 60o , 所 以∠BAD +∠ABE = 60o ,所以∠APB = 120o 。 我 们 观 察 到 在 点 P 运 动 的 过 程 中 ∠ A P B = 120o 是 固 定 角 度 , 且 ∠ A P B 所 对 的 线 段 AB 也 是 固 定 的 , 所 以 A 、 B 、 D 三 点 共 圆 , 其 中 AB 为 弦 , ∠APB 为圆周角。(理论基础 :同弦在同侧所对的圆周角相等 )如图,作圆O 使 得 A 、 B 、 D 三 点 共 圆 , 则 动 点 P 的 运 动 轨 迹 就 是 弧 AB , 连 接 O C 与 圆 O 交 于 点 P' ,则C P' 的 长 就 是 C P 的 最小值。(此题的关键点是找 P 点的运动轨迹,而找 P 点的运动轨迹的关键点是发现有定 线定角)
A B
D C
核心笔记3:
定理.外角等于内对角的四边形内接于圆。
如图, 已知四边形ABCD,若∠B+∠D=180°,则A,B,C,D四点共圆
A D
B C
(不常用不细说)
02
新课学习探究
发现规律
规律探究
解决问题
秘籍一:
知识原型:直径也是圆中的弦,并且是圆中最长的弦。 也就是说当圆中有某一固定长度线段AB为圆中的弦时,只有当AB为直径时,圆的直径才会最小。
A
D E
B
F
C
由于 BD 始终是圆中一条弦,当BD⊥ AC 时BD 有最小值,所以此时BD 为直径时圆的直径最小
PM ⊥l
规律总结
过直线(线段) 外一点P 与直线(线段)L 上一动点 所做的圆中,当 ������������ ⊥������ 时(也就是直线(线段) 与所做圆相切时)圆最小(直径、半径最短)
怎样判定四点共圆呢?下面的问题你需要做点笔记:
等线段共顶点:如图,若OA=OB=OC=OD,则A,B,C,D四点共圆
D A
O
B
C
核心笔记一 定理.对角互补的四边形内接于圆。
如图, 已知四边形ABCD,若∠B+∠D=180°,则A,B,C,D四点共圆
D A
O
B C
核心笔记2: 定理.从线段同一侧的两个点看向两个端点的张角相等,那么这四个点共圆。 如图,AC,BD相交于点P,若∠B=∠A,则A,B,C,D四点共圆
知识导引
为了解决好这个问题我们需要重温圆的定义:
什么叫做圆?请回答: 圆,到定点(原心)距离等于同一个常数(半径)的点的轨迹。
圆中半径处处相等的,这些点都在圆周上。
我们知道不共线的三点确定一个圆
那么怎么样的四点确定一个圆呢?这就是我们首先要搞清楚的第一各问题
四点共圆的问题?
【定义】如果同一平面内的四个点在同一个圆上,则称这四个点共圆, 一般简称为“四点共圆”。
秘籍二:
知识原型:圆的内接四边形对角一定互补,反之,对角互补的四边形四个顶点一定在同一个圆上。。
例2.如图,定长弦CD在以为AB直径的ΘO上滑动(点C、D与点A、B不重合),M 是CD
的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,求PM 长度的最大值
。
D C
M
A
B
P
O
思路)分析:
由于 M 是CD 的中点,所以,连接OM 后OM ⊥CD ,又因为CP⊥ AB ,所以在四边形OMPC 中,对角∠CPO+∠CMO=180o ,所以O 、M 、C 、P四点共圆,且OC为直径(由于OC为定 值 4,所以在运动的过程中圆的大小不变), PM 为弦,所以当MO⊥PO 时 PM 最大为圆的 直径。即 PM 最大就是等于OC 等于 4.(直径是圆中最长的弦)
我们下次课再见!
