第十章-梁的应力-习题答案
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算
解：危险截面在 A 处，其上之内力分量为： 弯矩： M y = FP1 a ， M z = FP2 H 扭矩： M x = FP2 a 轴力： FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心， 面边界交于 a、b 两点，这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用，最 大压应力值大于最大拉应力值，故 b 点为危险点，其应力状态如图所示。 10－7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解： （a）为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10－9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10－9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试：
1．假定骨骼为实心圆截面，确定横截面 B－B 上的应力分布； 2．假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成，忽略海绵状承受 应力的能力，确定横截面 B－B 上的应力分布；
工程力学作业10
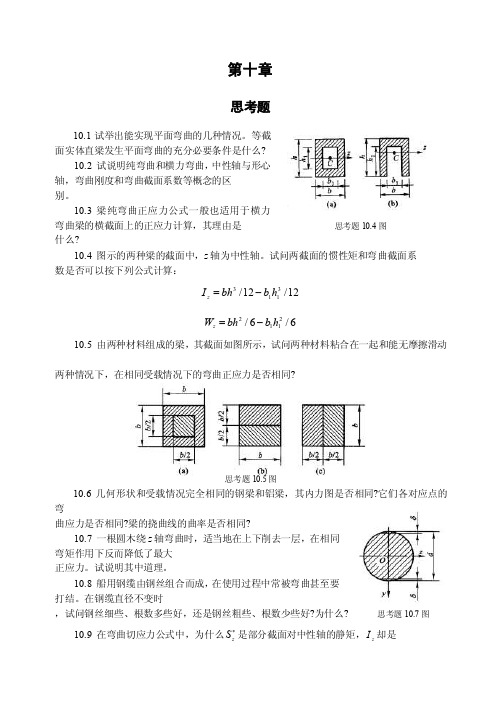
第十章思考题10.1试举出能实现平面弯曲的几种情况。
等截面实体直梁发生平面弯曲的充分必要条件是什么?10.2 试说明纯弯曲和横力弯曲，中性轴与形心轴，弯曲刚度和弯曲截面系数等概念的区 别。
10.3 梁纯弯曲正应力公式一般也适用于横力弯曲梁的横截面上的正应力计算，其理由是 思考题10.4图 什么?10.4 图示的两种梁的截面中，z 轴为中性轴。
试问两截面的惯性矩和弯曲截面系 数是否可以按下列公式计算：12/12/3113h b bh I z -= 6/6/2112h b bh W z -=10.5 由两种材料组成的梁，其截面如图所示，试问两种材料粘合在一起和能无摩擦滑动两种情况下，在相同受载情况下的弯曲正应力是否相同?思考题10.5图10.6 几何形状和受载情况完全相同的钢梁和铝梁，其内力图是否相同?它们各对应点的弯曲应力是否相同?梁的挠曲线的曲率是否相同?10.7 一根圆木绕z 轴弯曲时，适当地在上下削去一层，在相同弯矩作用下反而降低了最大 正应力。
试说明其中道理。
10.8 船用钢缆由钢丝组合而成，在使用过程中常被弯曲甚至要打结。
在钢缆直径不变时，试问钢丝细些、根数多些好，还是钢丝粗些、根数少些好?为什么? 思考题10.7图10.9 在弯曲切应力公式中，为什么*z S 是部分截面对中性轴的静矩，z I 却是整个截面对中性轴的惯性矩?10.10 试举出需要考虑梁的切应力强度的几种情形。
10.11 由四根100×80×10不等边角钢焊成一体的梁，在纯弯曲时截面按图示四种形式组合。
试问哪一种截面梁强度最高，哪一种最低?思考题10.11图 思考题1012图10.12 屋架梁常制成图示形状。
从材料力学角度看是否合理?为什么?10.13 图a 所示的钢梁和图b 所示的三角桁架材料相同，桁架两杆截面积之和 与钢梁截面积相等。
已知l =10h ，h =1.5b ，D =1.22b ，d =0.6D 。
结构力学练习题及答案
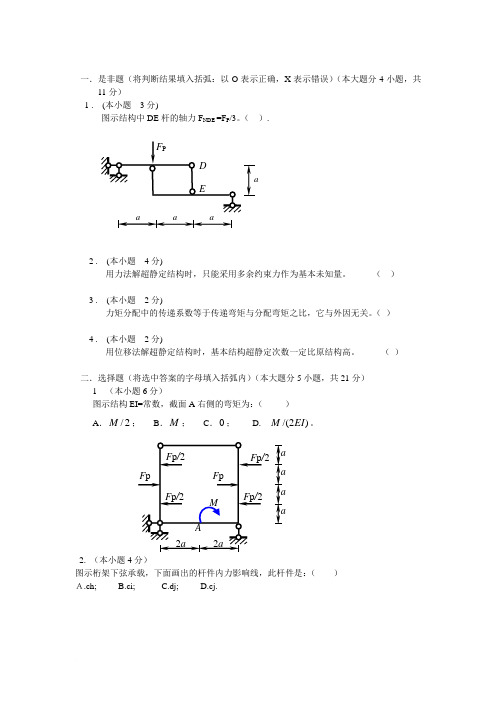
一．是非题（将判断结果填入括弧：以O 表示正确，X 表示错误）（本大题分4小题，共11分）1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
（ ）.2 . (本小题 4分)用力法解超静定结构时，只能采用多余约束力作为基本未知量。
（ ）3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比，它与外因无关。
（ ）4 . (本小题 2分)用位移法解超静定结构时，基本结构超静定次数一定比原结构高。
（ ）二．选择题（将选中答案的字母填入括弧内）（本大题分5小题，共21分） 1 （本小题6分）图示结构EI=常数，截面A 右侧的弯矩为：（ ）A ．2/M ；B ．M ；C ．0； D. )2/(EI M 。
2. （本小题4分）图示桁架下弦承载，下面画出的杆件内力影响线，此杆件是：（ ） Ａ.ch; B.ci; C.dj;D.cj.23. (本小题 4分)图a 结构的最后弯矩图为：A. 图b;B. 图c;C. 图d;D.都不对。
（ ）( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是： A.单位荷载下的弯矩图为一直线； B.结构可分为等截面直杆段； C.所有杆件EI 为常数且相同； D.结构必须是静定的。
( ) 5. （本小题3分）图示梁A 点的竖向位移为（向下为正）：( ) Ａ．F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三（本大题 5分）对图示体系进行几何组成分析。
F P=1四（本大题 9分）图示结构B 支座下沉4 mm ，各杆EI=2.0×105 kN ·m 2，用力法计算并作M 图。
五（本大题 11分） 用力矩分配法计算图示结构，并作M 图。
EI=常数。
六（本大题14分）已知图示结构，422.110 kN m ,10 kN/m EI q =⨯⋅=求B 点的水平位移。
工程力学习题 及最终答案
第一章第二章第三章绪论思考题1) 现代力学有哪些重要的特征？2) 力是物体间的相互作用。
按其是否直接接触如何分类？试举例说明。
3) 工程静力学的基本研究内容和主线是什么？4) 试述工程力学研究问题的一般方法。
第二章刚体静力学基本概念与理论习题2-1 求图中作用在托架上的合力F R。
12030200N习题2-1图页脚内容页脚内容2-2 已知F 1=7kN ，F 2=5kN, 求图中作用在耳环上的合力F R 。
2-3 求图中汇交力系的合力F R 。
2-4 求图中力F 2的大小和其方向角。
使 a )合力F R =1.5kN, 方向沿x 轴。
b)合力为零。
2-5 二力作用如图，F 1=500N 。
为提起木桩，欲使垂直向上的合力为F R =750N ，且F 2力尽量小，试求力F 2的大小和角。
245601习题2-2图(b)xy4530F 1=30NF 2=20NF3=40N A xy4560F 1=600NF 2=700NF 3=500NA 习题2-3图(a )x70F 2F 1=1.25kN A习题2-4图30F 1=500NAF 2页脚内容2-6 画出图中各物体的受力图。
(b)B (a )A (c)(d)DACDB页脚内容2-7 画出图中各物体的受力图。
2-8 试计算图中各种情况下F 力对o 点之矩。
习题2-6图(d)习题2-7图(a )C DB DABCBABC页脚内容2-9 求图中力系的合力F R 及其作用位置。
习题2-8图P (d)PF( a )F 3M =6kN m F 3F 2页脚内容2-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。
( a )q 1=600N/mq=4kN/m( b )q A =3kN/m习题2-9图( c ) F 4F 3页脚内容2-11 图示悬臂梁AB 上作用着分布载荷，q 1=400N/m ，q 2=900N/m, 若欲使作用在梁上的合力为零，求尺寸a 、b 的大小。
材料力学第六版答案第10章
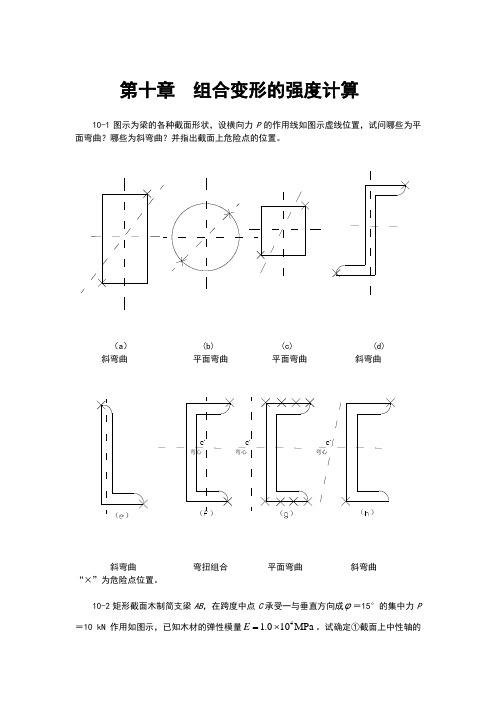
第十章 组合变形的强度计算10-1图示为梁的各种截面形状，设横向力P 的作用线如图示虚线位置，试问哪些为平面弯曲？哪些为斜弯曲？并指出截面上危险点的位置。
（a ） (b) (c) (d) 斜弯曲 平面弯曲 平面弯曲 斜弯曲弯心（）（）弯心弯心（）（）斜弯曲 弯扭组合 平面弯曲 斜弯曲“×”为危险点位置。
10-2矩形截面木制简支梁AB ，在跨度中点C 承受一与垂直方向成ϕ＝15°的集中力P ＝10 kN 作用如图示，已知木材的弹性模量MPa 100.14⨯=E 。
试确定①截面上中性轴的位置；②危险截面上的最大正应力；③C 点的总挠度的大小和方向。
解：66.915cos 10cos =⨯==οϕP P y KN59.215sin 10sin =⨯==οϕP P z KN4310122015=⨯=z J 4cm 3310cm W z =335625121520cm J y =⨯=3750cm W y =25.74366.94max =⨯==l P M y z KN-M 94.14359.24m ax =⨯==l P M z y KN-MMPaW M W M yy z z 84.9107501094.110101025.763633maxmax max=⨯⨯+⨯⨯=+=--σ 中性轴：οο47.2515tan 562510tan tan tan 411=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-=--ϕαy z J J 2849333105434.0101010104831066.948--⨯=⨯⨯⨯⨯⨯⨯==z y y EJ l P f m28933310259.010562510104831059.248--⨯=⨯⨯⨯⨯⨯⨯==y z z EJ l P f m 602.0259.05434.022=+=f cm方向⊥中性轴：ο47.25=α10-3 矩形截面木材悬臂梁受力如图示，P 1＝800 N ，P 2＝1600 N 。
工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第10章 组合受力与变形杆件的强度计算
网
FP a2
ww w
5
.k hd
b
m
上表面
∴
σa 4 = σb 3
习题 10－7 图
和 ε 2 。证明偏心距 e与 ε1 、 ε 2 之间满足下列关系：
FP
网
ww w
e=
ε1 − ε 2 h × ε1 + ε 2 6
课
后 答
案
FP
M = FP e
习题 10－8 图
解：1，2 两处均为单向应力状态，其正应力分别为： 1 处：
第10章
组合变形与变形杆件的强度计算
10－1 根据杆件横截面正应力分析过程， 中性轴在什么情形下才会通过截面形心？试分析 下列答案中哪一个是正确的。 （A）My = 0 或 Mz = 0， FN ≠ 0 ； （B）My = Mz = 0， FN ≠ 0 ； （C）My = 0，Mz = 0， FN ≠ 0 ； （D） M y ≠ 0 或 M z ≠ 0 ， FN = 0 。 正确答案是 D 。 解：只要轴力 FN x ≠ 0 ， 则截面形心处其拉压正应力一定不为零， 而其弯曲正应力一定为零， 这样使其合正应力一定不为零，所以其中性轴一定不通过截面形心，所以答案选（D） 。 关于中性轴位置，有以下几种论述，试判断哪一种是正确的。 （A）中性轴不一定在截面内，但如果在截面内它一定通过形心； （B）中性轴只能在截面内并且必须通过截面形心； （C）中性轴只能在截面内，但不一定通过截面形心； （D）中性轴不一定在截面内，而且也不一定通过截面形心。 正确答案是 D 。 解：中性轴上正应力必须为零。由上题结论中性轴不一定过截面形心；另外当轴力引起的 拉（压）应力的绝对值大于弯矩引起的最大压（拉）应力的绝对值时，中性轴均不在截面内， 所以答案选（D） 。 并且垂 10－3 图示悬臂梁中， 集中力 FP1 和 FP2 分别作用在铅垂对称面和水平对称面内， 直于梁的轴线，如图所示。已知 FP1＝1.6 kN，FP2＝800 N，l＝1 m，许用应力 σ ＝160 MPa。 试确定以下两种情形下梁的横截面尺寸： 1．截面为矩形，h＝2b； 2．截面为圆形。
钢筋混凝土第十章梁板结构试题答案
第十章梁板结构（408分）一、填空题（每空1分，共40分）1.《混凝土结构设计规范》规定：按弹性理论，板的长边与短边之比大于或等于3 时，称为单向板。
2.按弹性理论的计算是指在进行梁(板)结构的内力分析时，假定梁(板)为弹性体，可按结构力学方法进行计算。
3.单向板肋梁楼盖的板、次梁、主梁均分别为支承在次梁、主梁、柱和墙上的构件。
计算时对于板和次梁不论其支座是墙还是梁，均看成铰支座。
由此假定带的误差将通过折算荷载的方式来调整。
4.塑性铰的转动能力，主要取决于钢材品种、配筋率、混凝土极限压应变值。
5.在现浇单向板肋梁楼盖中，单向板的长跨方向应放置分布钢筋，分布钢筋的主要作用是承担长向实际存在的一些弯距、抵抗由于温度变化或混凝土收缩引起的内力将板上的集中荷载分布到更大的面积上、固定受力筋的位置。
6.钢筋混凝土塑性较与一般铰相比，其主要的不同点是只能单向转动且转动能力有限、能承受一定的弯矩、有一定的长度。
7.现浇肋梁楼盖的主次梁抗弯计算时,支座按矩形截面、跨中按 T型截面计算。
抗剪计算时均按矩形截面计算。
8.楼盖的内力分析中，如果按弹性理论，计算跨度取支座中心线之间的距离，如果按塑性理论，则净跨取之间的距离。
9.楼盖设计中，恒荷载的分项系数取为：当其效应对结构不利时，对有活荷载控制的组合，取 1.2 ，当其效应对结构有利时，对结构计算，取 1.0 ，对倾覆和滑移验算取 0.8 ；活荷载的分项系数一般情况下取 1.4 ，对楼面活荷载标准值大于4kN/m2的工业厂房楼面结构的活荷载，取 1.3 。
10.连续梁、板按调幅法的内力计算中，截面的相对压区高度应满足不大于0.35 ，调M的幅系数 一般不宜超过 0.2 ，调幅后，支座和跨中截面的弯矩值均应不小于0 M为按简支梁计算的跨中弯矩设计值。
1/3 ，其中11.现浇板在砌体墙上的支承长度不宜小于 120㎜。
12.无梁楼盖内力分析常用的方法有经验系数法、等代框架法。
材料力学第十章课后习题答案
第10章 疲劳强度的概念思考题10-1 什么是交变应力？举例说明。
答 随时间作周期性变化的应力称交变应力。
如下图所示的圆轴以角速度ω匀速转动，轴上一点A 的位置随时间变化，从A 到A ′，再到A ′′，再到A ′′′，又到A 处，如此循环往复。
轴上该点的正应力A σ也从0到，再到0，再到，又到0，产生拉压应力循环。
该点的应力即为交变应力。
+max σ−max σ10-2 疲劳失效有何特点？疲劳失效与静载失效有什么区别？疲劳失效时其断口分成几个区域？是如何形成的？答 （1）疲劳失效时的应力σ远低于危险应力u σ（静载荷下的强度指标）；需要经过一定的应力循环次数；构件（即使是塑性很好的材料）破坏前和破坏时无显著的塑性变形，呈现脆性断裂破坏特征。
（2）疲劳失效的最大工作应力σ远低于危险应力u σ；静载失效的最大工作应力σ为危险应力u σ。
（3）疲劳失效时其断口分成2个区域：光滑区域和颗粒状粗糙区域。
（4）构件在微观上，其内部组织是不均匀的。
在足够大的交变应力下，金属中受力较大或强度较弱的晶粒与晶界上将出现滑移带。
随着应力变化次数的增加，滑移加剧，滑移带开裂形成微观裂纹，简称“微裂纹”。
另外，构件内部初始缺陷或表面刻痕以及应力集中处，都可能最先产生微裂纹。
这些微裂纹便是疲劳失效的起源，简称“疲劳源”。
微裂纹随着应力交变次数的继续增加而不断扩展，形成了裸眼可见的宏观裂纹。
在裂纹的扩展过程中，由于应力交替变化，裂纹两表面的材料时而互相挤压、时而分离，这样就形成了断口表面的光滑区。
宏观裂纹继续扩展，致使构件的承载截面不断被削弱，类似在构件上形成尖锐的“切口”。
这种切口造成的应力集中，使局部区域内的应力达到很大数值。
最终在较低的应力水平下，由于累积损伤，致使构件在某一次载荷作用时突然断裂。
断口表面的颗粒状区域就是这种突然断裂造成的，所以疲劳失效的过程可以理解为裂纹产生、扩展直至构件断裂的一个过程。
10-3 什么是对称循环？什么是脉冲循环？ 答 对称循环是指最大应力与最小应力大小相等，正负号相反的应力循环。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习题10−1一工字型钢梁，在跨中作用集中力F，已知l=6m，F=20kN，工字钢的型号为20a，求梁中的最大正应力。
解：梁内的最大弯矩发生在跨中kN.m30max=M查表知20a工字钢3cm237=zW则MPa6.126Pa106.126102371030663maxmax=⨯=⨯⨯==-zWMσ10−2一矩形截面简支梁，受均布荷载作用，梁的长度为l，截面高度为h，宽度为b，材料的弹性模量为E，试求梁下边缘的总伸长。
解：梁的弯矩方程为()22121qxqlxxM-=则曲率方程为()()⎪⎭⎫⎝⎛-==2212111qxqlxEIEIxMx zzρ梁下边缘的线应变()()⎪⎭⎫⎝⎛-==2212122qxqlxEIhxhxzρε下边缘伸长为()2320221212EbhqldxqxqlxEIhdxxllzl=⎪⎭⎫⎝⎛-==∆⎰⎰ε10−3已知梁在外力作用下发生平面弯曲，当截面为下列形状时，试分别画出正应力沿横截面高度的分布规律。
解：各种截面梁横截面上的正应力都是沿高度线性分布的。
中性轴侧产生拉应力，另一bh侧产生压应力。
10−4 一对称T 形截面的外伸梁，梁上作用均布荷载，梁的尺寸如图所示，已知l =1.5m ,q =8KN/m ，求梁中横截面上的最大拉应力和最大压应力。
解：1、设截面的形心到下边缘距离为y 1则有 cm 33.741084104104841=⨯+⨯⨯⨯+⨯⨯=y则形心到上边缘距离 cm 67.433.7122=-=y于是截面对中性轴的惯性距为42323cm 0.86467.24101241033.3841284=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯=z I2、作梁的弯矩图设最大正弯矩所在截面为D ，最大负弯矩所在截面为E ，则在D 截面MPa 08.15Pa 1008.15100.8641033.710778.168231max t,=⨯=⨯⨯⨯⨯==--y I M z D σ MPa 61.9Pa 1061.9100.8641067.410778.168232max c,=⨯=⨯⨯⨯⨯==--y I M z D σ 在E 截面上MPa 40.5Pa 1040.5100.8641067.4100.168232max t,=⨯=⨯⨯⨯⨯==--y I M z E σ MPa 48.8Pa 1048.8100.8641033.7100.168231max c,=⨯=⨯⨯⨯⨯==--y I M z E σ 所以梁内MPa 08.15max t,=σ，MPa 61.9max c,=σC10−5 一矩形截面简支梁，跨中作用集中力F ，已知l =4m ，b =120mm ，h =180mm ，弯曲时材料的许用应力[σ]=10Mpa ，求梁能承受的最大荷载F max 。
解：梁内的最大弯矩发生在跨中 4max Fl M =矩形截面梁 62bh W z =则由 []σσ≤=z W M max max 得 []642bh Fl σ≤ 即 []N 64804318.012.021*******2=⨯⨯⨯⨯⨯=≤l bh F σ 10−6 由两个28a 号槽钢组成的简支梁，如图所示，已知该梁材料为Q235钢，其许用弯曲正应力[σ]=170Mpa ，求梁的许可荷载[F ]。
解：作弯矩图梁内的最大弯矩发生在跨中 F M 4max =矩形截面梁 3'max'max cm 656.6802====z z z z W y I y I W则由 []σσ≤=zW M maxmax 得 []z W F σ≤4 即 []N 28927410656.68010170466=⨯⨯⨯=≤-zW F σbh10−7 圆形截面木梁，梁上荷载如图所示，已知l =3m ，F =3kN ，q =3kN/m ，弯曲时木材的许用应力[σ]=10MPa ，试选择圆木的直径d 。
解：作弯矩图则由 []σσ≤=z W M max max 得 []σmax MW z ≥ 即 633101010332⨯⨯≤d π，得145mm m 145.0=≥d 10−8 起重机连同配重等重P =50kN ，行走于两根工字钢所组成的简支梁上，如图所示。
起重机的起重量F =10kN ，梁材料的许用弯曲应力[σ]=170Mpa ，试选择工字钢的型号。
设全部荷载平均分配在两根梁上。
解：设起重机左轮距A 端为x ，则有2650x M C -=，803862++-=x x M D从而确定出 kN.m 2.104max =C M ，kN.m 2.140max =D M 即梁内出现的最大弯矩为kN.m 2.140则由 []σσ≤=zW M max max 得 []3463max m 1025.810170102.140-⨯=⨯⨯=≥σM W z又对于本题 'max'max 2z z z z W y I y I W ===所以3344'cm 5.412m 10125.421025.82=⨯=⨯==--z zW W 查表选 25b 号工字钢。
10−9 两个矩形截面的简支木梁，其跨度、荷载及截面面积都相同，一个是整体，另一个是由两根方木叠置而成，试分别计算二梁中的最大正应力。
解：1、第一种情况梁内的最大弯矩发生在跨中 82max ql M =矩形截面梁 32632a bh W z == 则 3332max max 163283a ql a ql W M z =⨯⨯==σ 2、第二种情况梁内的最大弯矩发生在跨中 162max ql M =矩形截面梁 6632a bh W z == 则 3332max max 83166aql a ql W M z =⨯⨯==σ 10−10 直径d =0.6mm 的钢丝绕在直径D =600mm 的圆筒上，已知钢丝的弹性模量E =2×105MPa ，试求钢丝中的最大正应力。
解： 由zEI M=ρ1得 N.m 1024115.4103.03.064106.01023312411---⨯=⨯+⨯⨯⨯⨯==πρzEI M200MPa Pa 1020032106.01024115.43269333max =⨯=⨯⨯⨯===--ππσd M W M z 或200MPa Pa 10200103.03.0103.010263311maxmax =⨯=⨯+⨯⨯⨯==--ρσEy 10−11 一矩形截面简支梁由圆柱形木料锯成。
已知F =5kN ，a =1.5m ，[σ]=10Mpa 。
试确定弯曲截面系数最大时矩形截面的高宽比h :b ，以及梁所需木料的最小直径d 。
解：()66222b d b bh W z -== 由06322=-=b d db dW z 得 d b 33=，又022<-=b db W d z所以 d b 33=时 z W 取极大值，所以弯曲截面系数最大时，d b 33=，d h 36=，即 1:2:=b h 梁内的最大弯矩 kN.m 5.7max ==Fa M矩形截面梁 322736d bh W z == 则由 []σσ≤=zW M max max 得 []σmax MW z ≥即[]σmax3273M d ≥[]227mm m 227.01010105.739393633max==⨯⨯⨯=≥σM d 10−12 一铸铁梁如图所示。
已知材料的拉伸强度极限σb =150Mpa ，压缩强度极限σbc =630Mpa ，试求梁的安全因数。
解：1、设截面形心距离下边缘为y 1则有 mm 33.532160104016021201601020401601=⨯⨯+⨯⨯⨯⨯+⨯⨯=y则形心到上边缘距离 m m 67.14633.532002=-=y于是截面对中性轴的惯性距为42323mm 4.29013333267.6616010121601033.33401601240160=⨯⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯=z I 2、作梁的弯矩图C 截面MPa 057.22Pa 10057.22104.290133331033.531012612331max t,=⨯=⨯⨯⨯⨯==--y I M z C σ MPa 663.60Pa 10663.60104.290133331067.1461012612332max c,=⨯=⨯⨯⨯⨯==--y I M z C σ B 截面上MPa 442.40Pa 10442.40104.290133331067.146108612332max t,=⨯=⨯⨯⨯⨯==--y I M z B σ MPa 705.14Pa 10705.14104.290133331033.53108612331max c,=⨯=⨯⨯⨯⨯==--y I M z B σ 所以有 709.3442.40150t ==n ， t c 385.10663.60630n n >== ，取安全系数为3.709。
10−13 一简支工字型钢梁，工字钢的型号为28a ，梁上荷载如图所示，已知l =6m ，F 1=60kN ，F 2=40kN ，q =8kN/m ，钢材的许用应力[σ]=170Mpa ，[τ]=100Mpa ，试校核梁的强度。
解：作内力图12kN.m则有 MPa 8.170Pa 108.1701015.508108.86663max max =⨯=⨯⨯==-z W M σ 而[][]%5%47.01701708.170max <=-=-σσσ ][MPa 56.38Pa 1056.380085.01062.24107.80623max,max S,max ττ<=⨯=⨯⨯⨯==-bI S F z z 10−14 一简支工字型钢梁，梁上荷载如图所示，已知l =6m ，q =6kN/m ，F =20kN ，钢材的许用应力[σ]=170Mpa ，[τ]=100Mpa ，试选择工字钢的型号。
解：作内力图67.3kN86.8kN.m28kN57kN.m28kN由 []σσ≤=zW M max max 得 []33463max cm3.335m 10353.3101701057=⨯=⨯⨯=≥-σM W z 查表选25a （考虑5%误差可以选则22b ） 。
对于所选型号，梁内出现的最大切应力为 ][MPa 21.16Pa 1021.16008.01058.211028623max,max S,max ττ<=⨯=⨯⨯⨯==-bI S F z z （如为22b ，[]ττ<=MPa 8.15max ） 所以工字钢型号为25a （或22b ）。
10−15 由工字钢制成的简支梁受力如图所示。
已知材料的许用弯曲应力[σ]=170Mpa ，许用切应力[τ]=100Mpa 。