四位二进制全加全减器
四位二进制全加器设计

四位二进制全加器设计(总3页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除组合逻辑电路课程设计题目:用74ls283构成四位二进制全加/减器一、设计思路74ls283为四位加法器,而如果希望进行减法运算,则需要将其转化为加法,而之前学到,二进制运算,一个数减去另一个数,即等于加上其补码。
于是得到如下公式,A-B=A+(-B)=A+B’+1。
将其全部视为加法运算,即一个数加上一个正数或者一个负数,这个数为加数B。
那么,需要将加数增添一位符号位,以区分正负。
因为74ls283芯片的引脚为低位向正在运算的数的进位,所以可以将其作为加数的符号位。
当其为正数时,输入为0,即计算A+B。
而当加数为负数时候,使其输入为1,并将B取反,再加上进位1,正好与公式相符。
根据以上原理,应用输入作为符号位,进行4位被加(减)数与5位加(减)数的加法运算。
设A3-A0为被加(减)数,B3-B0为加(减)数,M0为符号位。
当M0为0时表示正数,为1时表示负数。
而当B为负数需要取反时,刚好可以利用异或门的特性来进行,即1异或B等于B’,0异或B等于B即将B的各个数位和M0通过异或门相连,即可以做到负数取反。
二、电路图如图,输入输出ABC都用LED来指示二进制的数值,开关S2控制A的数值,S1控制B的数值以及符号位。
BX1指示灯指示的是输入B经过异或门作用后的电平。
三、由于此电路进行的是加法运算,两个加数一共2的9次方中组合,所以真值表又多又显而易见,此处将不给出。
四、举例演示:(1)5+6=11如图拨动开关,A=5,B=6,可见C为11的二进制表示1011。
(2)7-3=4如图,将M0置为1以表示负数。
BX1表示的是3的反码,在74283中进行了加1的运算即变成了补码,输出结果为0100(2)=4(10)(3)1000+1000=10000由于输出只有四位,而1000+1000会产生进位。
组合逻辑课程设计4位二进制全加器全减器原创

关键字 74LS283 全加器、四位二进制、迭代电路、并行进位、串行进位、VHDL
摘要
加法器是数字系统中产生数的和的装置。加数和被加数为输入,和数与进 位为输出的装置为半加器。若加数、被加数与低位的进位数为输入,而和数与进
...
.
..
..
位为输出则为全加器。例如:为了节省资源,减法器和硬件乘法器都可以用加法 器来构成。但宽位加法器的设计是很耗资源的,因此在实际的设计和相关饿得设 计与开发中需要注意资源的利用率和进位速度两方面的问题,多位加法器的构成 主要有两种:并行进位和串行进位。并行进位加法器设有并行进位产生逻辑,运 行速度比串行进位快;串行进位是将全加器采取并行级联或菊花链式级联构成多 位加法器。加法器也是常用作计算机算术逻辑部件,执行逻辑操作、移位与指令 调用。此外还可以用来表示各种数值,如:BCD、加三码,主要的加法器是以二 进制作运算。
1 0 0100 11011000
1 0 0101 00011010
1 0 0001 10011100
1 0 0001 10111110
1 0 1010 01000111
1 0 1010 01101001
1 0 0010 01000011
1 0 0010 01100101
... ... ... ... ... ... ... ... ... ... ... ... ... ...
4bitalu加法器工作原理

4bitalu加法器工作原理
4位二进制加法器(4-bit binary adder)是一种电子电路,用于将两个4位二进制数相加。
最常见的4位二进制加法器是基于全加器(Full Adder)的设计。
以下是4位二进制加法器的工作原理:
输入:
4位二进制加法器有两个4位的输入,通常表示为A和B。
每一位都可以是0或1。
全加器:
4位二进制加法器由4个全加器组成,每个全加器都用于处理对应位的加法。
全加器的结构:
每个全加器包括三个输入:A的对应位(Ai)、B的对应位(Bi)和前一位的进位(Ci-1)。
输出包括两个部分:当前位的和(Si)和传递到下一位的进位(Ci)。
第一位的处理:
第一位的全加器只有两个输入,即A0和B0,因为没有前一位的进位。
输出为第一位的和(S0)和传递到第二位的进位(C1)。
中间位的处理:
对于中间的三位,每个全加器都有三个输入(Ai、Bi、Ci-1)和两个输出(Si、Ci)。
输出的和(Si)作为当前位的二进制和。
输出的进位(Ci)传递到下一位的进位输入(Ci-1)。
最后一位的处理:
最后一位的全加器输出的和(S3)和进位(C4)即为4位二进制数相加的结果。
进位检测:
如果最后一位的全加器输出的进位(C4)为1,则表示溢出。
输出:
4位二进制加法器的输出为一个4位的二进制数,其中每一位都是相应位的和。
总体而言,4位二进制加法器通过级联多个全加器,逐位相加并处理进位,实现对两个4位二进制数的加法运算。
这种结构也可以扩
展到更多位数的二进制加法器。
四位二进制超前进位全加器

•超前进位加法原理
A0 B0
C-1 A0 B0 A1 B1
C-1 A0 A1B0 B1 A2 B2 C-1 A0 A2 B0 B2 A3 B3 C-1 A0 A3 B0 B3
……
…
…
0 C-1 FA0
C0 进位逻辑
C0 FA1
C1 进位逻辑
C1 FA2
C2 进位逻辑
C2 FA3
C3 进位逻辑 C3
S0
0
C0
C1
C2
C3
C-1
FA0
FA1
FA2
FA3
S0
S1
S2
C3
S3
CO ∑
CI CI
CI
A3 B3
C2
S2
CO ∑
CI CI
CI
A2 B2C1S1Fra bibliotekCO ∑
CI CI
CI
A1 B1
所求结果为:C3S3S2S1S0
S3
C0
S0
CO ∑
CI CI
CI
A0 B0
C0-1
超前进位全加器-----74LS283
S1
S2
S3
• 进位输入是由专门的“进位逻辑门”来提供 • 该门综合所有低位的加数、被加数及最低位进位输入
超前进位加法器使每位的进位直接由加数和被加数产生, 而无需等待低位的进位信号
Si Ai Bi Ci1 Ci Ai Bi AiCi1 BiCi1
定义两个中间变量Gi和Pi : Gi= AiBi ……产生变量 Pi= Ai+Bi ……传输变量 Ki= GiPi = Ai ⊕Bi ……中间变量
全加器真值表
输入端:Ai、Bi、Ci-1
课程设计--四位二进制加减法器

组合逻辑电路课程设计之四位二进制加减法器摘要:加法器即是产生数的和的装置。
加数和被加数为输入,和数与进位为输出的装置为半加器。
若加数、被加数与低位的进位数为输入,而和数与进位为输出则为全加器。
对于4位的二进制加法,相关的有五个的量:1,被加数A ,2,被加数B ,3,前一位的进位CIN ,4,此位二数相加的和S ,5,此位二数相加产生的进位COUT 。
前三个量为输入量,后两个量为输出量,五个量均为4位.本文采用4位二进制并行加法器原理,选择74LS283,74LS283是4位二进制先行进位加法器,它只用了几级逻辑来形成,并连接几个异或门,由其构成4位二进制加法器/减法器,并用Verilog HDL 进行仿真。
关键字:全加器,异或门,74LS283, verilog,加法/减法功能.总的电路设计 一.硬件电路的设计本电路74LS283为核心元件,其逻辑符号为U174LS283DSUM_410SUM_313SUM_14SUM_21C49B411A412B315A314B22A23B16A15C07全加器由加位输入X 和Y ,还有进位输入CIN,3个输入的范围是0~3,可以用两个输出位表示.S(全加和)和COUT(送给高位的进位).满足下面等式.CINY CIN X Y X COUT CINY X CIN Y X N CI Y X N CI Y X CIN Y X S ⋅+⋅+⋅=⋅⋅+⋅'⋅'+'⋅⋅'+'⋅'⋅=⊕⊕=实现全加器的电路图如下74LS08D本电路还需要4个异或门,要实现加法器和减法器的双重功能,需要有选择功能端,设A为四位二进制被加数,B为二进制被减数.当使能端为0时,电路实现加法运算,当使能端为1时电路实现减法运算.电路原理图如下1.Multisim原理图2.MAX plus2原理图当A口输入为0011,B口输入为0001,使能端为0时.输出为0100.电路图如下当A口输入为0011,B口输入为0001,使能端输入为1时.输出为0010.电路图如下二.软件程序设计Verilog HDL语言程序module b(A,B,C,D,E);input[3:0] A,B;input C;output[3:0] D;output E;assign {E,D}=C?(A+B):(A-B);endmodule当A口输入为0011,B口输入为0001,使能端输入为0,输出为0010,仿真图如下.当A口输入为0011,B口输入为0001,使能端输入为1时.输出为0010.仿真图如下三.总结及心得体会1.通过本次课题设计,自学了一些相关的Verilog语言和MAX+plusII,Multisim 软件的使用方法.2.基本掌握了74LS283的基本原理及使用方法.。
quartus_4位二进制加减法计数器
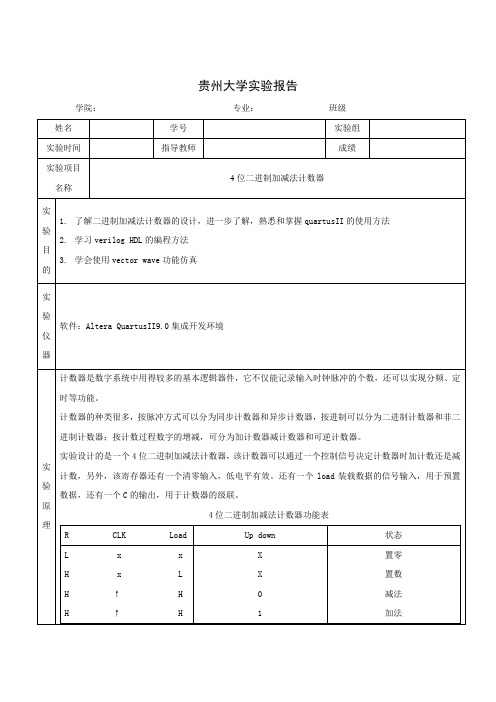
贵州大学实验报告学院:专业:班级设计原理框图从原理图中可见,需要有1bit装载位(load)、1bit清零位(clr)、方向控制位up_down和4bit数据选择位DIN[3..0]。
装载位我们采用SW0,清零位采用SW1,方向控制位为SW2。
SW3-SW6作为数据输入端,LED1-LED4显示数据的输出,LED5为溢出标志位。
实验内容编写一个带预置输入,清零输入,可加可减计数器的verilog代码或VHDL代码并仿真,编译下载验证module counter4(load,clr,c,DOUT,clk,up_down,DIN);//定义模块input load;//定义输入信号input clk;//wire load;//定义线网型input clr;//wire clr;//input up_down;//wire up_down;//input [3:0]DIN;//定义4位二进制输入信号wire [3:0]DIN;// 定义4位二进制线网型信号output c;//定义输出信号reg c;//定义寄存器类型信号output [3:0]DOUT;//wire [3:0]DOUT;reg [3:0]data_r;assign DOUT=data_r;always@(posedge clk or posedge clr or posedge load)//检测clk,clr,load的上升沿beginif(clr)//当clr=1的时候进行下面的运行程序data_r<=0;//将data_r置零else if(load) //当load=1的时候进行下面的运行程序data_r<=DIN;//将DIN的值赋给data_relse begin if(up_down)//load=0的时候进行下面的操作beginif(data_r==4'b1111)begin///当data_r==4'b1111的时候进行下面的运行程序data_r<=4'b0000;c=1;endelse begin//当data_r不等于4'b1111的时候进行下面的运行程序data_r<=data_r+1;//进行加法计数c=0;endendelsebeginif(data_r==4'b0000)begin//当data_r==4'b0000的时候进行下面的运行程序data_r<=4'b1111;c=1;endelse begin//当data_r不等于4'b1111的时候进行下面的运行程序data_r<=data_r-1;//进行减法计数c=0;endendendendendmodule//结束模块实验数据如图为波形仿真结果,当clr为1的时候,输出结果为0000;当clr为0,load为1时,输出结果为输入数据DIN的值,当up_down为1时,加法进位,进行加1运算,当data_r达到1111时,data_r变为0000,级零信号c为1;当up_down为0时,减法进位,进行减1运算,当data_r达到0000时,data_r变为1111,级零信号c为0。
4位同步二进制加法计数器计数最大值

4位同步二进制加法计数器是一种常见的数字电路,用于实现二进制计数。
它可以将二进制数字表示为电信号,并且在每次输入脉冲时进行递增。
下面将详细介绍4位同步二进制加法计数器及其计数的最大值。
一、4位同步二进制加法计数器的原理1. 4位同步二进制加法计数器由4个触发器组成,每个触发器对应一个二进制位。
当输入一个脉冲时,每个触发器根据前一位的状态以及输入脉冲的信号进行状态转换。
这样就实现了二进制数的递增。
2. 触发器之间通过门电路连接,用于控制触发器状态的变化。
这些门电路可以根据具体的设计选择不同的逻辑门,常见的有AND门、OR 门、NOT门等。
3. 4位同步二进制加法计数器是同步计数器,即所有触发器同时接收输入脉冲,确保计数的同步性。
二、4位同步二进制加法计数器的计数最大值1. 4位二进制数的表示范围是0~15,因此4位同步二进制加法计数器的计数最大值为15。
2. 在计数到15后,再输入一个脉冲,计数器将重新从0开始计数,即实现了循环计数。
三、4位同步二进制加法计数器的应用1. 4位同步二进制加法计数器常用于数字电子钟、信号发生器等数字电路中,用于实现计数和定时功能。
2. 它还可以作为其他数字电路的组成部分,用于构建更复杂的逻辑功能。
3. 在数字系统中,计数器是十分重要的组件,它能够实现数字信号的计数和控制,广泛应用于各种数字系统中。
4位同步二进制加法计数器是一种重要的数字电路,通过它可以实现对二进制数的递增计数。
其计数的最大值为15,应用领域广泛。
希望本文内容能够对读者有所启发。
四、4位同步二进制加法计数器的工作原理4位同步二进制加法计数器是一种晶体管数字集成电路,它利用触发器和逻辑门等基本元件构成,能够实现二进制数字的加法计数。
在4位同步二进制加法计数器中,每个触发器代表一个二进制位,通过输入脉冲的控制,能够实现对二进制数的递增计数。
具体来说,当输入一个脉冲信号时,4位同步二进制加法计数器会根据触发器之间的连线和逻辑门的作用,根据之前的状态和输入脉冲的信号进行状态转换,从而实现二进制数的递增。
全加器全减器设计实验报告

全加器全减器设计实验报告1. 引言全加器和全减器是数字电路中常用的基本电路模块之一。
全加器用于将两个二进制数相加,全减器用于将两个二进制数相减。
在本实验中,我们将设计并实现一个4位的全加器和一个4位的全减器电路。
2. 原理2.1 全加器全加器是由两个半加器和一个或门组成的电路。
一个半加器用于计算两个输入位的和,另一个半加器用于计算进位值。
将两个半加器的结果和进位值通过或门进行运算,即可得到全加器的输出。
如下图所示为全加器的逻辑电路图:其中,A和B为输入信号,用于表示待相加的两个二进制数的对应位;S为输出信号,表示两个输入数的对应位相加的结果;C为进位信号,表示相加时产生的进位。
2.2 全减器全减器是由两个半减器和一个与非门组成的电路。
与全加器类似,一个半减器用于计算两个输入位的差,另一个半减器用于计算借位值。
将两个半减器的结果和借位值通过与非门进行运算,即可得到全减器的输出。
如下图所示为全减器的逻辑电路图:其中,A和B为输入信号,用于表示待相减的两个二进制数的对应位;D为输出信号,表示两个输入数的对应位相减的结果;B为借位信号,表示相减时需要借出的位。
3. 设计和实现3.1 全加器设计根据2.1中的原理,我们可以使用两个半加器和一个或门来实现一个4位的全加器电路。
根据全加器的逻辑电路图,我们可以将四个输入位(A0, A1, A2, A3)依次与另外四个输入位(B0, B1, B2, B3)连接到两个半加器中,然后将两个半加器的和(S0, S1, S2, S3)通过或门进行运算。
此外,计算进位值需要使用到四个位的与门(And)。
具体电路图如下:3.2 全减器设计根据2.2中的原理,我们可以使用两个半减器和一个与非门来实现一个4位的全减器电路。
根据全减器的逻辑电路图,我们可以将四个输入位(A0, A1, A2, A3)依次与另外四个输入位取反连接到两个半减器中,然后将两个半减器的差(D0, D1, D2, D3)通过与非门进行运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字逻辑设计及应用课程设计报告
组合逻辑设计
题目:使用74LS83构成4位二进制全加\全减器。
具体要求:1)列出真值表;
2)画出逻辑图;
3)用Verilog HDL 进行仿真;
1.设计思路及原理分析
全加器是除本位数字相加外,还考虑进位输入和进位输出的加法器,全减器同理,考虑借位输入和借位输出。
本次主要应用74LS83来实现设计要求,74LS83是四位二进制先行进位加法器,可以直接接入输入获得全加器,所以设计重点在于四位全减器的设计。
对于串行进位加法器,可略加改进获得相应的减法器,基本原理如下式:
2'2'2'2'[]s s s s X Y X Y -=+-
'2'2[]2n s s Y Y -=-
这里利用了补码的基本性质,具体实现时可以将减数逐位取反,然后最低位加1。
又因为全加器时in C 为为进位输入,全减器时应变为借位输入,所以要减去in C ,且全加器的输出端out C 为进位输出,而全减法器应该输出借位输出,而进位输出与借位输出恰好是反向的关系,所以将0S 取反后即得到全减器的借位输出out B ,据此,可以在全加器的基础上设计全减器。
其中表中输出部分上行为全加输出,下行为全减输出。
2 逻辑电路图
3 电路实现和仿真
3.1 verilog HDL设计代码如下:
module add(s,out,a,b,in,EN);
output[0:3] s;
output out;
input[0:3] a,b;
input in;
input EN;
reg out;
reg[0:3] s,c;
always@(*)
if (EN==0)
begin
{out,s}=a+b+in;
end
else
begin
c=10000-b;
{out,s}=a+c-in;
out=~out;
end
endmodule
3.2 仿真波形图
4 结果分析
由波形图可知,仿真结果与真值表完全吻合,说明本次设计的可行性和正确性,至此,我们完成了基于74LS83构成4位二进制全加\全减器的分析、设计、仿真,而且达到了预期的设计要求。
5 总结
此次课程选取的题目较为简单,容易操作,但与平时课上所学习的基础知识联系紧密,是对课上所学理论知识很好的应用和检验。
过程中最大的感受是体会到了如何用课本所学的理论设计所需的电路,而理论和实践起来是不同的,即使理论很扎实,而实际用verilog HDL语言来写时也会遇到很多困难。
但是在设计时能对所学的东西有更好的理解,这也更激起了我对数字设计这门课程的兴趣,以后一定会继续好好学习这门课程,课下将书本上的verilog HDL程序用Quartus仿真出来,以加深对知识的理解。
6 参考文献
《数字设计—原理与实践》 John F.Wakerly
《基于Quartus II的数字系统Verilog HDL设计实例详解》周景润。
