13-1 准静态过程 功 热量【热力学】
合集下载
热力学第一定律
W 绝 热 V V 1 2pd p 1 V V 1 1 [V V 1 2 () 1 1 ]1 1 [p 1 V 1 p 2 V 2 ]
例4.3 P.183
已知T1 =300 K, p2/p1 =10和p2 /p1 =100，则T=?
m x x=0(平衡位置)
例4.4 P.184
Q是系统所吸收的能量，W是外界对系统所
U2U1QW作的功
d U d Q d或 W d Q d U pd V
热力学第一定律12
一、定体热容与内能
定体比热容cv ，定压比热容cp
p
b
d
定体摩尔热容Cv,m, 定压摩尔热容 Cp,m
c
a
e
等体过程a—b, dV=0
T+dT
T
(ΔQ)v = ΔU
0 V
c V lT i0( m m Q T )V lT i0 (m T u)V ( T u)V
三、可逆与不可逆过程
系统从初态出发经历某一过程变到末态，若可以找到一个能使系统和外界都复原的过程（这时系统回到 初态，对外界也不产生任何影响），则原过程是可逆的。若总是找不到一个能使系统与外界同时复原的过程， 则原过程是不可逆的。
例如：气体向真空自由膨胀就是一个不可逆过 程。
判断条件
真空
•系统回到初态 •对外界也不产生任何影响
一、理想气体内能
热力学第一定律12 1、自由膨胀过程
C
A
B
焦耳实验 理想气体宏观特性：
U1 (T1 ,V 1) =U2 (T2 ,V2)=常量
证明：理想气体内能仅是状态的函数，与体积 无关，称为焦耳定律
满足pV=νRT关系；满足道尔顿分压定律； 满足阿伏加德罗定律；满足焦耳定律U=U(T)。
例4.3 P.183
已知T1 =300 K, p2/p1 =10和p2 /p1 =100，则T=?
m x x=0(平衡位置)
例4.4 P.184
Q是系统所吸收的能量，W是外界对系统所
U2U1QW作的功
d U d Q d或 W d Q d U pd V
热力学第一定律12
一、定体热容与内能
定体比热容cv ，定压比热容cp
p
b
d
定体摩尔热容Cv,m, 定压摩尔热容 Cp,m
c
a
e
等体过程a—b, dV=0
T+dT
T
(ΔQ)v = ΔU
0 V
c V lT i0( m m Q T )V lT i0 (m T u)V ( T u)V
三、可逆与不可逆过程
系统从初态出发经历某一过程变到末态，若可以找到一个能使系统和外界都复原的过程（这时系统回到 初态，对外界也不产生任何影响），则原过程是可逆的。若总是找不到一个能使系统与外界同时复原的过程， 则原过程是不可逆的。
例如：气体向真空自由膨胀就是一个不可逆过 程。
判断条件
真空
•系统回到初态 •对外界也不产生任何影响
一、理想气体内能
热力学第一定律12 1、自由膨胀过程
C
A
B
焦耳实验 理想气体宏观特性：
U1 (T1 ,V 1) =U2 (T2 ,V2)=常量
证明：理想气体内能仅是状态的函数，与体积 无关，称为焦耳定律
满足pV=νRT关系；满足道尔顿分压定律； 满足阿伏加德罗定律；满足焦耳定律U=U(T)。
热力学第一定律
21
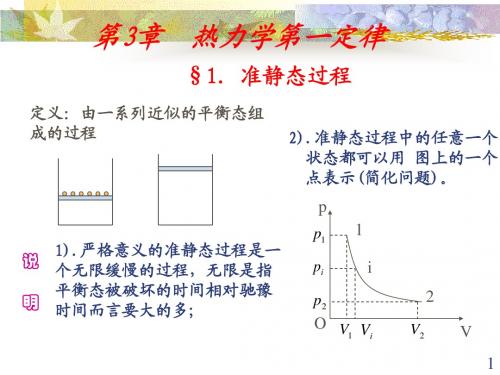
例1: 一定量的理想气体从体积V1 膨胀到体积V2 ，经历 以下几个过程： AB等压过程； AC等温过程； AD绝热 过程。问：从P－V图上，(1) 哪一个过程做功较多？哪 一个过程做功较少？(2) 经历哪一个过程内能增加？经 历哪一个过程内能减少？(3) 经历哪一个过程吸热最多？ P 解： (1) 等压过程做功最多 A A A P A B p T Q 绝热过程做功最少 P C
例2：图示两卡诺循环，S1 = S2 P (1) 吸热和放热差值是否相同？ (2) 对外所做净功是否相同？ (3) 效率是否相同？ 答案：(1)相同；(2)相同；(3)不相同
讨论
T2 1 )卡诺热机效率C 1 T1
只与T1和T2有关
与物质种类、膨胀的体积无关
2 ) 理论指导作用
T1 提高 c T2
提高高温热源的温度现实些
31
3)理论说明低温热源温度T2 0
说明热机效率 且只能 进一步说明 •热机循环不向低温热源放热是不可能的
T
(2) 等压膨胀：系统吸热 O V1 V2 V 系统内能增加，且对外做功； 等温膨胀：系统吸热，全部用来对外做功，内能不变； 绝热膨胀：系统不吸收热量，靠减少系统的内能对外做功
PQ
D
等压：内能增加；等温：内能不变；绝热：内能减少。
(3) 等压膨胀过程吸热最多。（4）绝热线比等温线陡 22
例2: 一mol单原子理想气体在汽缸中，设汽缸与活塞无 摩擦，开始时，P1=1.013*105Pa， V1=1.0*10 –2m3 ，将 此气体在等压下加热，使其体积增大一倍，然后在等体 下加热至压强增大一倍，最后绝热 膨胀为起始温度。 (1)画P-V图(2)求内能的增量(3)过程中的功 解： (1)图示 (2)0 (3) P2
大学物理热力学基础-准静态过程-功-热量内能
2
如果其中有一个状态为非平衡态，则此过程不是准静 态过程。如果系统进行的速度过快，系统状态发生变 化后，还未来得及恢复新的平衡态，系统又发生了变 化，则该过程也不是准静态过程。
例如：气缸活塞压缩的速
度过快，气体的状态发生
变化，还来不及恢复，P、
F
V、T 无确定关系，则此过
程为不是准静态过程。
3
PA
量为0。 dT 0 2.过程方程 PV C
恒 温 源 T
P 1
P1
3.过程曲线
4.功 A V2 PdV V1
P2 o V1
T
2 V2 V
17
由理想气体状态方程
P m RT
V
RT
V
A V2 RT dV RT V2 dV
V1
V
V V1
等温过程的功
A RT ln V2 m RT ln V2
m RT ln P1
P2
19
三、等压过程
1.过程特点
系统的压强不变 dP 0
P
2.过程曲线
3.内能增量
E m i RT
2
1
2
P
4.功 压强不变
o
V1
V2 V
A
V2 V1
PdV
P
V2
V1
dV
P (V2 V1 )
PV
20
5.热量
QP E A
m
14
热力学第一定 律在等值过程
中的应用
15
一、等容过程
1.过程特点
V
系统的体积不变 dV = 0
系统对外做功为0 dA = 0 2.过程曲线
如果其中有一个状态为非平衡态，则此过程不是准静 态过程。如果系统进行的速度过快，系统状态发生变 化后，还未来得及恢复新的平衡态，系统又发生了变 化，则该过程也不是准静态过程。
例如：气缸活塞压缩的速
度过快，气体的状态发生
变化，还来不及恢复，P、
F
V、T 无确定关系，则此过
程为不是准静态过程。
3
PA
量为0。 dT 0 2.过程方程 PV C
恒 温 源 T
P 1
P1
3.过程曲线
4.功 A V2 PdV V1
P2 o V1
T
2 V2 V
17
由理想气体状态方程
P m RT
V
RT
V
A V2 RT dV RT V2 dV
V1
V
V V1
等温过程的功
A RT ln V2 m RT ln V2
m RT ln P1
P2
19
三、等压过程
1.过程特点
系统的压强不变 dP 0
P
2.过程曲线
3.内能增量
E m i RT
2
1
2
P
4.功 压强不变
o
V1
V2 V
A
V2 V1
PdV
P
V2
V1
dV
P (V2 V1 )
PV
20
5.热量
QP E A
m
14
热力学第一定 律在等值过程
中的应用
15
一、等容过程
1.过程特点
V
系统的体积不变 dV = 0
系统对外做功为0 dA = 0 2.过程曲线
热力学第一定律
Qdb=Edb+Adb=Eab-Ead+Adb=208.4-167.2+0=41.2J 13
§3.4 热容量，热力学第一定律对理想气体的应用
一.等容摩尔热容量
摩尔热容量：一摩尔物质(温度T时)升高1度所吸收的热量,即
Cm
1
dQ dT
单位:J/mol•K
一般C与温度有关，也与过程有关，可以测量。
原平衡态
非平衡态
新平衡态
热力学中研究过程时，为了在理论上能利用系 统处于平衡态时的性质,引入准静态过程的概念.
二.准静态过程: 1.在过程中的任意时刻,系统都无限的接近平衡 状态,准静态过程是由无数个平衡态组成的过程.
2.准静态过程是实际过程的理想化模型. (无限缓慢)有理论意义,也有实际意义. 3
对于理想气体的等容过程,
dQ dE i RdT
2
1 dQ i
CV .m
dT
R 2
dA 0
C v.m i R 2
T2
E E2 - E1 CV.m dT
T1
E
C V.m
T
14
注意：对于理想气体,公式 E = Cv T 不仅适用于等容过程，而且适用于任何过程。
如图，作一个辅助过（等容+等温） 连接始末两点 E辅 EV + ET
系统 （ T1 ）直接与 热源 （ T2 ）有限温差
T2 热传导为非准静态过程
系统 T1
T1+△T T1+2△T T1+3△T T2
保持系统与外界无穷小温差， 每一无穷小传热过程为等温过程, 过程“无限缓慢”即可看成准静态传热过程.
10
三.热力学第一定律
对于任一过程
§3.4 热容量，热力学第一定律对理想气体的应用
一.等容摩尔热容量
摩尔热容量：一摩尔物质(温度T时)升高1度所吸收的热量,即
Cm
1
dQ dT
单位:J/mol•K
一般C与温度有关，也与过程有关，可以测量。
原平衡态
非平衡态
新平衡态
热力学中研究过程时，为了在理论上能利用系 统处于平衡态时的性质,引入准静态过程的概念.
二.准静态过程: 1.在过程中的任意时刻,系统都无限的接近平衡 状态,准静态过程是由无数个平衡态组成的过程.
2.准静态过程是实际过程的理想化模型. (无限缓慢)有理论意义,也有实际意义. 3
对于理想气体的等容过程,
dQ dE i RdT
2
1 dQ i
CV .m
dT
R 2
dA 0
C v.m i R 2
T2
E E2 - E1 CV.m dT
T1
E
C V.m
T
14
注意：对于理想气体,公式 E = Cv T 不仅适用于等容过程，而且适用于任何过程。
如图，作一个辅助过（等容+等温） 连接始末两点 E辅 EV + ET
系统 （ T1 ）直接与 热源 （ T2 ）有限温差
T2 热传导为非准静态过程
系统 T1
T1+△T T1+2△T T1+3△T T2
保持系统与外界无穷小温差， 每一无穷小传热过程为等温过程, 过程“无限缓慢”即可看成准静态传热过程.
10
三.热力学第一定律
对于任一过程
大学物理第4章-热力学第一定律
mol 理想气体的内能：
i E νRT 2
理想气体的内能是温度 T 的单值函数
i ΔE νR ΔT 2
QUIZ Jack’s death due to the loss of a) love b) temperature c) heat d) internal energy
热量是过程量，内能是状态量。
二、热 量
dQ 0 表示系统从外界吸热； dQ 0 表示系统向外界放热。
在SI制中：焦耳(J)
准静态过程中传递的热量是过程量。
三、热量的单位
结 论：
热量和功是系统状态变化中伴随发生的两种 不同的能量传递形式。它们的物理本质不同 宏观运动 分子热运动 功 热量 分子热运动 分子热运动
作功和传热的大小不但与系统的初、末态有关， 而且与过程有关，它们都是过程量，不是状态量， 因而微量功和微量传热分别写成 dA和dQ,它们不是全 微分。
dQ Cp ( )p dT
摩尔定压热容 Cp,m
i i Q E A RT RT 1 RT 2 2
Cp，m 1 dQ i 1 R dT p 2
：摩尔数
i：自由度数
三、迈耶公式及比热容比 摩尔定体热容 CV,m 摩尔定压热容 Cp,m 迈耶公式 比热容比
CV,m 3 R 2
5 R 2
Cp,m 5 R 2 7 R 2
1.67 1.40
刚性多原子分子
3R
4R
1.33
思考：为什么理想气体任意两状态间内能的变 化可表示成摩尔定体热容 CV,m 与温度变化乘积 的关系，而不是摩尔定压热容 Cp,m 与温度变化 乘积的关系？
new热力学第一定律
当气体作无摩擦的准静态膨胀或压缩时， 为了维持气体的平衡态，外界的压强必然 等于气体的压强。 II v2
A dA PdV
I v1
说明
A＝ pdV
V1
V2
P
•系统所作的功与系统的始末状态有关， 而且还与路径有关，是一个过程量。
•气体膨胀时，系统对外界作功 气体压缩时，外界对系统作功 系统对外界所作的 •作功是改变系统内能的一种方法 •本质：通过宏观位移来完成的：机械运动→ 功等于pV 图上过 分子热运动 程曲线下面的面积
V2 M i Q R(T2 T1 ) pdV V1 2 理想气体的压强保持不变，p=const
•过程方程：
•内能、功和热量的变化
A
V2
V1 V2 T1 T2
pdV p(V
2
V 1)
•特征：
系统吸收的热量一部分 用来增加系统的内能， 另一部分使系统对外界 作功。
V1
Q p U 2 U1 p(V2 V1 )
为从平衡态破坏到新平 衡态建立所需的时间称 为弛豫时间。
3、准静态过程
如果一个热力学系统过程在始末两平衡态之间所经历的之 中间状态，可以近似当作平衡态，则此过程为准静态过 程。 •准静态过程只有在进行的“无限缓慢”的条件下才可 能实现。 •对于实际过程则要求系统状态发生变化的特征时间远 远大于弛豫时间才可近似看作准静态过程。
又根据PV n C，有P1V1n P2V2n C，所以
A
P2V2nV 21n 1 n
PV1nV11n P2V2 PV1 PV1 P2V2 1 1 1 1 n 1 n n 1
15.3 内能 热力学第一定律
一、内能
热力学系统的能量取决于系统的状 态——内能。 M i
A dA PdV
I v1
说明
A＝ pdV
V1
V2
P
•系统所作的功与系统的始末状态有关， 而且还与路径有关，是一个过程量。
•气体膨胀时，系统对外界作功 气体压缩时，外界对系统作功 系统对外界所作的 •作功是改变系统内能的一种方法 •本质：通过宏观位移来完成的：机械运动→ 功等于pV 图上过 分子热运动 程曲线下面的面积
V2 M i Q R(T2 T1 ) pdV V1 2 理想气体的压强保持不变，p=const
•过程方程：
•内能、功和热量的变化
A
V2
V1 V2 T1 T2
pdV p(V
2
V 1)
•特征：
系统吸收的热量一部分 用来增加系统的内能， 另一部分使系统对外界 作功。
V1
Q p U 2 U1 p(V2 V1 )
为从平衡态破坏到新平 衡态建立所需的时间称 为弛豫时间。
3、准静态过程
如果一个热力学系统过程在始末两平衡态之间所经历的之 中间状态，可以近似当作平衡态，则此过程为准静态过 程。 •准静态过程只有在进行的“无限缓慢”的条件下才可 能实现。 •对于实际过程则要求系统状态发生变化的特征时间远 远大于弛豫时间才可近似看作准静态过程。
又根据PV n C，有P1V1n P2V2n C，所以
A
P2V2nV 21n 1 n
PV1nV11n P2V2 PV1 PV1 P2V2 1 1 1 1 n 1 n n 1
15.3 内能 热力学第一定律
一、内能
热力学系统的能量取决于系统的状 态——内能。 M i
热力学基础1
0.1kg水蒸气自120℃加热升温至140℃， 水蒸气自120℃加热升温至140℃ 例3. 0.1kg水蒸气自120℃加热升温至140℃，求等 体过程和等压过程各吸收了多少热量？内能各变化多 体过程和等压过程各吸收了多少热量？ 各作了多少功？ 少？各作了多少功？ 解： 已知 M = 18×10−3 kg⋅ mol −1 CV ,m = 27⋅ 82J ⋅ mol −1⋅ k −1
系统内能的增量只与系统起始和终了状态有 关，与系统所经历的过程无关 .
二 热力学第一定律
Q = (E2 − E1) +W
系统从外界吸收热量， 系统从外界吸收热量，一部分使系统内能 增加， 增加，另一部分使系统对外做功 —— 热力学第一定律
热力学第一定律 讨论： 讨论：
Q = (E2 − E1) +W
C p, m =
PV =
dQp dT
m RT M
m W = ∫ dW = ∫ pdV = p(V2 −V1 ) = R(T2 − T1 ) V1 M m m ∆E = Qp −W = (Cp,m − R)(T2 −T1)= CV ,m (T2 −T1 ) M M
V2
C p,m − CV ,m = R
p
A*
2 1 *B
p
A*
2 1 *B
WA1B +QA1B =WA2B +QA2B
∆EAB = C
o
V
WA1B2A + QA1B2A = 0
∆E A1B 2 A = 0
o
V
理想气体内能 : 表征系统状态的单值函数 , 理想气体的内能仅是温度的函数 .
E = E (T )
一般气体： 一般气体：
大学物理热力学基础
绝热系数 C p,m CV ,m
dQ dE pdV
3. 等温过程
p
p1
I
T=恒量，dT=0，dE=0。
p2
QT WT pV RT
O V1
WT
pdV RT V2 dV RT ln V2
V V1
V1
QT
RT ln V2
V1
RT ln
p1 p2
C p,m
(dQ) p dT
Q
C p,m (T2
T1 )
m M
C p,m (T2
T1 )
三、热力学第一定律
某一过程，系统从外界吸热 Q，对外界做功 W，系统 内能从初始态 E1变为 E2，则由能量守恒：
Q (W ) E Q E W
规定 Q>0，系统吸收热量；Q<0,系统放出热量； W>0，系统对外作正功；W<0,系统对外作负功；
理想气体 E m i RT M2
理想气体的内能就是理想气体的热能.
准静态过程的功
dx
当活塞移动微小位移dx时， 系统对外界所作的元功为：
dW Fdx pSdx pdV
p FS
光滑
系统体积由V1变为V2，系统对外界作总功为：
W dW V2 pdV V1 系统对外作正功； 系统对外作负功； 系统不作功。
)
R(T2
T1
)
(
i 2
R
R)(T2
T1
)
pV RT
等压过程中系统吸收的热量一部分用来增加 系统的内能，一部分用来对外做功。
第3 章 热力学第一定律
§ 4 热力学第一定律 一、热力学第一定律 二、理想气体的摩尔热容 三、经典热容理论的局限性
热力学第一定律：关于系统在状态变化中能量 遵循的规律 。
一、热力学第一定律 1. 内容（107） 公式 成立条件
Q E2 E1 A 初末态是平衡态
dQ dE dA 适用一切过程 一切系统
2.若加一些条件 若为准静态 若为理想气体 若理气准静态
第 3 章 热力学第一定律 §1 热力学过程分类 §2 功 准静态过程中体积功的计算 §3 热 热量的计算 §4 热力学第一定律 §5 绝热过程 §6 循环过程和热机
§1 热力学过程的分类 一、 分类 二、改变热力学状态的两种能量交换形式
一、热力学过程 1.定义：系统状态发生变化的过程 2.分类：准静态过程与非静态过程
计算系统对外作的功
p
S
dl
设活塞面积为 S，在某一 时刻，压强为 ，p 气体 推动活塞移动 dl
气体对外作功为：
dA pSdl pdV
2）公式1 ： 微小过程 dA P dV
公式2：有限过程 注意：准静态过程 2.体积功的图示：
V2
A PdV
V1
P
1）P~V图曲线下的面积。
V
2）关于功---过程量的图示。 示功图
②结论：“无限缓慢”的过程是准静态过程。 二. 改变系统热力学状态的两种方式
1.方式 有两种
作功:外界 系统 传热:外界 系统
2.举例： 1） 从外界传热 2） 利用外界作功
T1 T2
§2 内能 功
一、系统的内能 1.内能的微观构成：
分子热运动的动能，分子间的相互作用能， 分子、原子内的能量，原子核内的能量， 等等。 通常，经过一个热力学过程，发生变化的只 是和热运动相关的那部分能量。
大学物理热力学基础知识点及试题带答案
热力学基础一、基本要求1. 理解功、热量及准静态过程的概念。
2. 掌握热力学第一定律，能分析计算理想气体等容、等压、等温过程和绝热过程中的功、热量、内能改变量；理解循环过程概念及卡诺循环的特征，并能计算效率和致冷系数。
3. 了解可逆过程、不可逆过程及卡诺定理。
4. 了解热力学第二定律及其统计意义。
二、主要内容1. 准静态过程：过程进行的每一时刻，系统的状态都无限接近平衡态。
准静态过程可以用状态图上的曲线表示。
2. 热力学第一定律（1） 热力学第一定律的数学表达式Q=E 2 - E 1 +Ｗ对微分过程为dQ=dE +d Ｗ热力学第一定律的实质是能量守恒与转换定律在热现象中的应用，其内容表示系统吸收的热量一部分转换为系统的内能，一部分对外做功。
（2） 准静态过程系统对外做功：d Ｗ=pd Ｖ ，Ｗ=⎰12V V pd Ｖ（3） 热量：系统和外界之间或两个物体之间由于温度不同而交换的热运动量，热量也是过程量。
一定摩尔的某种物质，在某一过程中吸收的热量，)(C m12m c,T T M Q -=（4） 摩尔热容：1mo1物质温度变化1K 所吸收或放出的热量，定义式为 dTＱd m,=m c C 其中m 为1mo1 物质吸热。
摩尔定容热容：ＣV , m =摩尔定压热容：Ｃp, m =理想气体的摩尔热容：ＣV, m =，Ｃp, m =Ｃp, m =ＣV, m + 摩尔热容比：=3. 热力学第一定律对理想气体等值过程和绝热过程的应用，详见表1 表1 d =0 =恒量=恒量p =恒量mmmM m Ｔ1nMm Ｔ1nＣV, m =Ｃp, m =4. 循环过程（1）循环过程的特征是E =0热循环：系统从高温热源吸热，对外做功，向低温热源放热，致效率为== 1—致冷循环：系统从低温热源吸热，接受外界做功，向高温热源放热，致冷系数为==（2）卡诺循环：系统只和两个恒温热源进行热交换的准静态循环过程。
卡诺热机的效率为= 1—卡诺致冷机的致冷系数为三、习题与解答1、 如图所示，一定量的空气，开始在状态A ，其压强为2.0×105Pa ，体积为2.0 ×10－3m 3 ，沿直线AB 变化到状态B 后，压强变为1.0 ×105Pa ，体积变为3.0 ×10－3m 3 ，求此过程中气体所作的功.解 S ABCD ＝1/2(BC ＋AD)×CD 故 W ＝150 J2、 汽缸内储有2.0mol 的空气，温度为27 ℃，若维持压强不变，而使空气的体积膨胀到原体积的3倍，求空气膨胀时所作的功. 解 根据物态方程11RT pV v =, 则作功为()J 1097.92231112⨯===-=RT pv V V p W v3、64g 氧气（可看成刚性双原子分子理想气体）的温度由0℃升至50℃，〔1〕保持体积不变；(2)保持压强不变。