信号与系统 §4.4非周期信号的频谱变换
合集下载
信号与系统-信号与系统的频域分析

§3.1 周期信号的分解与合成
1768年生于法国 1807年提出“任何周期信号都可用收敛 的正弦函数级数表示” 1829年狄里赫利第一个给出收敛条件 拉格朗日反对发表 1822年首次发表在“热的分析理论”一 书中。
§3.1 周期信号的分解与合成
一、周期信号分解为三角级数
周期信号 f t,周期为T1
F () 0 0
F () , j
F () 0 0
说明:
F() F(0) f (t)dt
0
时域积分性质多用于F(0)=0的情况,而F(0)=0表明f(t)的频谱函数中直
0
2
bn
2 T
T
2 T
2
f
(t)sin n1tdt
4 T
T
2 0
Asin
n1tdt
图1
T
4A T
co sn1t n1
2 0
4 A (n 1, 3, 5,) nπ 0 (n 2, 4, 6,)
所以f( t )的傅里叶级数为
f
(t )
4A π
(sin
1t
1 3
sin
31t
1 5
sin
51t
)
2
( n1 )
)
A Sa( n1 )
2
T
2
其中Sa( )形式如下。
抽样函数:
Sa(t) sin t t
Sa (0) 1
当 t k (k 1,2,3 时,) Sa( t ) = 0
图6
f( t ) 的双边谱
Sa( t ) : Fn :
图7
周期矩形脉冲信号含有无穷多条谱线,也就是说,周期矩形脉冲信号 可表示为无穷多个正弦分量之和。在信号的传输过程中,要求一个传输系 统能将这无穷多个正弦分量不失真地传输显然是不可能的。实际工作中, 应要求传输系统能将信号中的主要频率分量传输过去,以满足失真度方面 的基本要求。周期矩形脉冲信号的主要能量集中在第一个零点之内, 因而, 常常将ω=0~ 这段频率范围称为矩形脉冲信号的频带宽度。记为
《信号与线性系统分析》第四章

三、 正交函数集
n个函数 g 1(t)g ,2(t) ,gn(t) 构成一函数集,
如在区间 (t1, t2 ) 内满足正交特性,即
t1 t2gi(t)gj(t)d t0 (ij)
t2 t1
gi2(t)dtKi
那么此函数集称为正交函数集
2021/9/18
21
在〔t1,t2〕区间,任意函数f(t) 可由n个正交的函数的 线性组合近似
那么称正交。
t2 t1
f1(t)f2(t)d
t0
正交的条件:
2021/9/18
17
例: f(t)11
(0t) (t2)
试用sint 在区间〔0,2 π〕来近似 f(t)。
2021/9/18
f(t)
c12
1 0
1
2
t
18
2
解:
f (t)sintdt
c12 0 2 sin2tdt
0
1
2
[0sitndt (sitn )d]t
权积分表示〞 ——傅里叶的第二个主要论点
2021/9/18
9
变换域分析:
频域分析:--傅里叶变换
自变量为 j
复频域分析:--拉氏变换
自变量为 S = +j
Z域分析:--Z 变换 自变量为z
zesT e(j )T
2021/9/18
10
§4.1 信号分解为正交函数
正交矢量 正交函数 正交函数集 用完备正交集表示信号
s t0T t0
in1 (ts)in (m1t)td T 2
0
mn mn
tt00Tco(nsω1t)co(m sω1t)d t T 0 2
mn mn
§4.3 周期信号的频谱§4.4 非周期信号的频谱

T
1 傅里叶反变换式 j t f (t ) F (j ) e d 2 F(jω)称为f(t)的傅里叶变换或频谱密度函数,简称频谱。 f(t)称为F(jω)的傅里叶反变换或原函数。
也可简记为
f(t) ←→F(jω)
或F(jω) =ℱ [f(t)] f(t) = ℱ-1[F(jω)] F(jω)一般是复函数,写为 F(jω) = | F(jω)|e j (ω) = R(ω) + jX(ω) 说明 (1)前面推导并未遵循严格的数学步骤。可 证明,函数f(t)傅里叶变换存在的充分条件: f (t ) d t
Fn
0.15 π 2 1
0.25 π
1
1
O
0 .15 π
▲
0 .5
1.12
1
1.12
0 .5
2 1
2 1
2 1 1
O
1
0.25 π
■
第 8页
二、周期信号频谱的特点
举例:有一幅度为1,脉冲宽 度为的周期矩形脉冲,其周 期为T,如图所示。求频谱。
1 f(t) 0 …
▲ ■ 第 11 页
三.频带宽度
1.问题提出
T
Fn
2π
O
2
第一个零点集中了信号绝大部分能量(平均功率) 由频谱的收敛性可知,信号的功率集中在低频段。
▲ ■ 第 12 页
周期矩形脉冲信号的功率
1 P T
0
T
f (t )dt
2
1 1 以τ s,T s为 例 , 取 前5 次 谐 波 20 4 2 2 2 2 2 2 2 2 P5n F0 F1 F2 F3 F4 F1 F2 F3 F4
1 傅里叶反变换式 j t f (t ) F (j ) e d 2 F(jω)称为f(t)的傅里叶变换或频谱密度函数,简称频谱。 f(t)称为F(jω)的傅里叶反变换或原函数。
也可简记为
f(t) ←→F(jω)
或F(jω) =ℱ [f(t)] f(t) = ℱ-1[F(jω)] F(jω)一般是复函数,写为 F(jω) = | F(jω)|e j (ω) = R(ω) + jX(ω) 说明 (1)前面推导并未遵循严格的数学步骤。可 证明,函数f(t)傅里叶变换存在的充分条件: f (t ) d t
Fn
0.15 π 2 1
0.25 π
1
1
O
0 .15 π
▲
0 .5
1.12
1
1.12
0 .5
2 1
2 1
2 1 1
O
1
0.25 π
■
第 8页
二、周期信号频谱的特点
举例:有一幅度为1,脉冲宽 度为的周期矩形脉冲,其周 期为T,如图所示。求频谱。
1 f(t) 0 …
▲ ■ 第 11 页
三.频带宽度
1.问题提出
T
Fn
2π
O
2
第一个零点集中了信号绝大部分能量(平均功率) 由频谱的收敛性可知,信号的功率集中在低频段。
▲ ■ 第 12 页
周期矩形脉冲信号的功率
1 P T
0
T
f (t )dt
2
1 1 以τ s,T s为 例 , 取 前5 次 谐 波 20 4 2 2 2 2 2 2 2 2 P5n F0 F1 F2 F3 F4 F1 F2 F3 F4
《信号与系统》教与学第四章
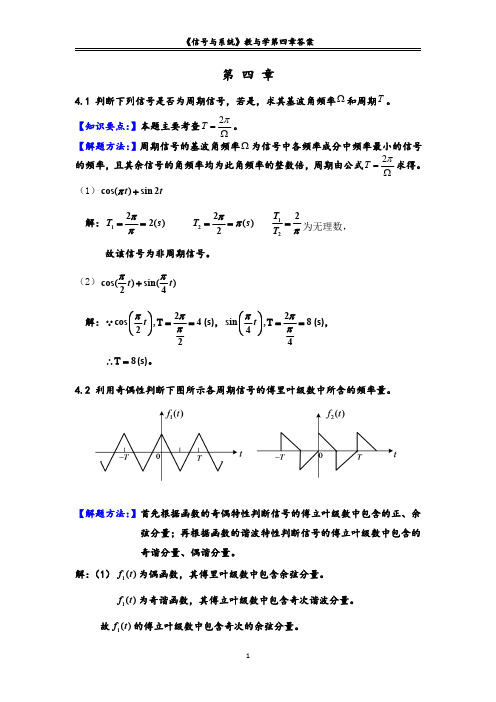
j n e 3
j n
e3
1 n
sin
n 3
,
n
0, 1,
2,
2
《信号与系统》教与学第四章答案
4.4 周期信号 f (t ) 的双边频谱 Fn 如图所示,求其三角函数表达式。
【知识要点:】本题主要考查周期信号的频谱概念,单边谱与双边谱的关系。
(3)计算信号的功率。
【知识要点:】本题主要考查周期信号的频谱概念应用;帕斯瓦尔功率等式应用。
T
2
;
f
t
A0 2
n1
An
cos
nt n
;P
Fn 2 。
n
【解题方法:】利用已知条件观察求出 ,并带入公式计算求出各次谐波分量;
根据单边幅度谱和双边幅度谱的关系、单边相位谱和双边相位谱的关系画出双
边幅度谱和相位谱;最后利用帕斯瓦尔功率等式计算信号的功率。
解:(1)
x
t
16 cos
20
t
4
6
cos
30
t
6
4
cos
40
t
3
10 (rad/s) ,
T
2
2 10
1 (s) , 5
周期信号所含谐波次数为二次,三次,四次;
求得。
(1) cos( t ) sin 2t
解: T1
信号与系统—信号的频域分析

2. 指数形式傅立叶级数
连续时间周期信号可以用指数形式傅立叶级数表示为
f (t) Cn e jn0t
n =
其中
Cn
1 T
T 2 T
fT (t)e jn0t dt
2
n 1 两项的基波频率为f0,两项合起来称为信号的基波分量 n 2 的基波频率为2f0,两项合起来称为信号的2次谐波分量
n N 的基波频率为Nf0,两项合起来称为信号的N次谐波分量
3.卷积性质
若f1(t)和f2(t)均是周期为T0的周期信号,且 f1(t) C1n , f2 (t) C2n
则有 f1(t) * f2 (t) T0C1n C2n
4. 微分特性
若
则有
f (t) Cn
f '(t) jn0Cn
5. 对称特性
(1)若f(t)为实信号
则 | Cn || Cn | n n
• 周期信号f(t)可以分解为不同频率虚指数信号之和
fT (t) Cn e jn0t
n =
不同的时域信号,只是傅里叶级数的系数Cn不同, 因此通过研究傅里叶级数的系数来研究信号的特性。
Cn是频率的函数,它反映了组成信号各正弦谐波 的幅度和相位随频率变化的规律,称频谱函数。
2、频谱的表示
直接画出信号各次谐波对应的An、 Cn线状 分布图形,这种图形称为信号的频谱图。
)
例2 试计算图示周期三角脉冲信号的傅立叶级数展开式。
f (t)
-2 1 0 2
t
解: 该周期信号f (t)显然满足狄里赫勒的三个条件,Cn存在
Cn
1 T
T 2 T
f (t)e jn0t dt 1 ( 0 te jn0t dt 2 1
信号与系统课程第06讲 非周期信号的分解——傅里叶变换

信号与系统——非周期信号的分解—傅里叶变换
1
第06 讲
上一页 返 回
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
本章主要内容
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱 4.4 非周期信号的频谱 4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
2 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱
4.4 非周期信号的频谱
4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
3 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
1
0
+ j 0 j +
F ( j ) = 1
2 +2
(
)
=
−
arctan
2
o
( )
o
− 2
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
12
双边指数信号
f (t ) = e− t − t
0
e− t (t)
f (t)e− j t dt =
−
0 e( − j )t dt +
当T→∞时,有 → d , n → , →
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
7
∵
F( j) = lim 2Fn ,则
T →
F( j)
lim
T →
Fn
1
第06 讲
上一页 返 回
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
本章主要内容
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱 4.4 非周期信号的频谱 4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
2 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱
4.4 非周期信号的频谱
4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
3 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
1
0
+ j 0 j +
F ( j ) = 1
2 +2
(
)
=
−
arctan
2
o
( )
o
− 2
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
12
双边指数信号
f (t ) = e− t − t
0
e− t (t)
f (t)e− j t dt =
−
0 e( − j )t dt +
当T→∞时,有 → d , n → , →
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
7
∵
F( j) = lim 2Fn ,则
T →
F( j)
lim
T →
Fn
非周期信号

第一章 信号及其描述
因此: ① 离散谱就变成了连续谱。 ② 求和运算则可用积分运算代替。
∞
x (t ) =
∫
−∞
ω0 ( 2π
∫
∞
−∞
x ( t ) e − jn ω 0 t dt ) e
jn ω 0 t
因为 1/T=ω0/2π当 T→∞,ω0=△ω→dω,n ω0 →ω ∞ 1 ∞ − jω t jω t x (t ) = ∫ ( x ( t ) e dt ) e dω ∫ −∞ − ∞ 2π 令:
∫
∞
−∞ ∞
x ( t ) cos 2 π ftdt x ( t ) sin 2 π ftdt
∫
−∞
① 若:x(t) 为实的偶函数,则其富氏变换 x(f) 为:
R e x ( f ) = 2 ∫ x ( t ) cos 2π ftdt
0
∞
I m x( f ) = 0
故:x(f) 是 f 的偶函数又是实函数。即 Rex(f) = x(-f)
设复数 Z=a+bi.当 b≠0 时.z 就叫虚数.a=0,b≠0 时 z 叫纯虚数。
第一章 信号及其描述
作用与定义: 作用与定义:
∞ −∞
x( f ) =
∫
x ( t ) e − j 2 π ft dt = R e x ( f ) − jI m x ( f )
Re x( f ) = Im x( f ) =
1 x (ω ) = 2π
∫
∞
−∞
x ( t ) e − j ω t dt
jω t
FT
x (t ) =
∫
∞
−∞
x (ω ) e
dω
IFT
第四章(1)周期信号的傅里叶级数和频谱

1 j n jnt f ( t ) An e e 2 n
1 j n j n 令复数量 2 An e Fn e Fn
,称其为复
Fn
傅里叶系数,简称傅里叶系数。其模为
,
相角为 n , 则得傅里叶级数的指数形式为 :
f (t )
n
F e
n
jnt
复傅里叶系数
n 2 , 4 , 6 , 8 ,...... n 1 , 3 , 5 , 7 ,.....
, 0 bn 4 n ,
4
1 1 1 f t [sin t sin3t sin5t .... sinnt ...] 3 5 n
2
0
T 2
2 an 0 T
n 0,1 , 2 , 3,.......
2 bn T 2 T
0
T 2 T 2
f ( t ) si nnt dt
2 T2 (1) si nnt dt T
0
T 2 0
si nnt dt
T 2
2 1 2 1 cosnt cosnt T T n T n 0
a0 an cos(nt ) bn sin(nt ) 2 n1 n 1 2 其中 an , bn 称为傅里叶系数, 。 T
那么,傅里叶系数如何求得呢?
T 2 T 2
a0 1 2 T
f ( t )dt
T 2 2 an T f ( t ) cos(nt )dt T 2 T b 2 2 f ( t ) sin( t )dt n n T T 2
A0 1 1 j n jnt j n jnt Ane e Ane e 2 2 n 1 2 n 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(t ) 1 1 Sgn(t )
22
1 2
( )
1
Sgn(t )
1
2
j
(t) F ( j) () 1 j
ε (t)
1
1/2
0
t
-1/2
R( ) ( )
X
(
)1Biblioteka ()3 22,
,
0 0
常用傅立叶变换
(t) 1
1(直流) 2 ()
e t (t )
1
j
e |t|
• 各频率分量的频率不成谐波关系
傅立叶变换存在的充分条件
1、f(t) 在有限区间上具有有限个极值和有限个第一类
间断点; 2、绝对可积:
| f (t) | dt
允许奇异函数也能满足上述条件 ——阶跃、冲激一类函数也存在傅立叶变换。
典型非周期信号的频谱
• 单边指数信号 • 双边指数信号 • 矩形脉冲信号 • 符号函数 • 单位冲激信号 • 冲激偶信号 • 单位阶跃信号
e
t
t 0 t 0
t 0 t 0 t 0
Sgn(t)
1
Sgn(t )
lim
0
f1 (t )
t 0 -1
F1( j)
0 e t e jt dt
e t
0
e
jt dt
2 j 2 2
F(
j)
lim
0
F1 (
j)
2
j
2
j
Sgn(t) 2
j
(5)阶跃函数的频谱
阶跃函数可以看作是
直流信号与符号函数之和:
f1 t e t , 0
t 0
F1
j
0 e t e jwt dt
e t e jwt dt
0
2 2 2
f(t)
e |t|
2 2
2
F(jw)
2
1
0
t
0
例4:求如图所示信号的 Fourier 变换。
f 2 t
e t
0
t
e t
X2(w)
●1
0
1●
信号可以写为 :
f2
t
无穷小时,n
引入频谱密度的概念:
F j lim T
Fn 1
lim FnT T
T
-T/2
频谱演变的定性观察
1
2
T1
F (n1 )
T/2
F (n1 ) 1
F (n1 )
-T/2
T/2
1
2
2
从周期信号 FS 推导非周期的 FT
f
(t )
n
Fn
n
T
e
jnt
1 T
T
FnT
2 f (t )e jnt dt
例1:求如图所示门函数的频谱。
g (t)
解:门函数可以表示为:
1
g
t
1
0
t
2
t
2
F ( j ) f (t )e jtdt
2
1
e
jt
dt
2
0
2
F j
j
j
e 2 e 2
2sin( )
2
2
j
2
4
0
2
t
4
sin( )
2
Sa
2
2
g (t )
Sa
2
e t t
• 冲激函数导数的频谱可以表示为:
t
e jt dt d e jt
j
dt
t 0
t j
推论:
n j n
(3)单位直流信号的频谱
f (t) 1 F ( j)e jtd
2
f(t) 1
首先看()的傅立叶反变换f1(t):
t
f1(t)
1
2
()e jtd 1
2
0
即:1
2
T 2
Fn
1 T
T
2 f (t ) e jnt dt
T 2
1
离散值变连续量dw
T 2
T
2
lim F
j
def
FnT
T
f (t )e jwt dt
def
f (t)
1
F(
j
)e
jwt dw
2
一对 Fourier 变换对
F ( j ) f (t )e jtdt
f (t ) 1 F ( j )e jtd
§4.4 非周期信号的频谱 -----Fourier 变换
• Fourier 变换 • 奇异函数的 Fourier 变换
一、Fourier 变换
(Fourier transform——FT)
周期信号:fT (t),当T fT (t)变为非周期信号。
1 d T 2 2
T
无穷小 d
0时,是离散变量
例2:求:单边指数函数的频谱。
解:F j f (t )e jt dt
0
t
e t e jt dt
0
1
j
0
et (t )
1
j
| F ( j) |
1
2 2
0
() tg 1
( )
F j 1
0
2
0
2
例3:求双边指数函数的频谱。
e |t|
1
解:双边指数函数可以表示为:
e t
e
t
频谱函数为:
t 0 t 0
0
F2 j et e jt dt e t e jt dt
0
1
1
2
j
j
j2 2
R2 (w) 0
2
X 2 (w ) 2 2
二、奇异函数的 Fourier变换
(1)冲激函数的频谱
(t)
F ( j )
(t) 1
(1)
0
t
2 2 2
g
(t
)
Sa(
2
)
Sgn(t)
2
j
(t)
( )
1
j
t j
推论:
n (t) j n
F ( j ) F f (t ) f (t )e jtdt
f (t ) F-1 F ( j ) 1 F ( j )e jtd
2
傅立叶反变换 f(t)为F(jw)的原函数
从物理意义来讨论傅立叶变换
• F(jω)是一个密度函数的概念 • F(jω)是一个连续谱 • F(jω)包含了从零到无限高频的所有频率分量
1
0
(t) F ( j) (t)e jt dt
f (t) (t)dt f (0)
F ( j) e j0 1
冲激函数δ(t) 的频谱是常数1。也就是说,δ(t) 中
包含了所有的频率分量, 而各频率分量的频谱密度都
相等。 显然, 信号δ(t) 实际上是无法实现的。
(2)冲激函数导数的频谱
2
记为: f (t ) F ( j )
频谱密度是一复函数,可以写为如下的形式:
F ( j ) F ( j ) e j R jX
F ( j ) f ( t )e jt dt f (t ) 1 F ( j )e jt d 2 傅立叶正变换 F(jw)为f(t)的频谱密度函 数(频谱函数)
( f1 t)
F1( j) ()
F ( j)
f (t) 1 2f(1 t)
2 F1( j) F( j) 2 ()
1 2 ()
(2 )
0
(t)
t
F ( j)
1
f (t)
1
t
2 ()
傅立叶变换的对偶性
(4)符号函数的频谱
1
Sgn(t )
0
符号函数定义为:
1
令:f1
t
e t
