第三章非周期信号的频谱
合集下载
§305 典型非周期信号的频谱

lim E
e j e j
j
E
lim
2
sin
2E
lim
ቤተ መጻሕፍቲ ባይዱ
sin
2E
F
2E
O
E 2E
时域无限宽,频带无限窄
lim
Sa
( )
X
四.符号函数
不满足绝对
e te j t dt
0
1
j
1
j
2
j2 2
F
lim
0
F1
lim
0
2
j2
2
2
j
X
频谱图
sgnt
2
j 2
2
j
e2
j
F
2
2
2
F 是偶函数
信号与系统
§3.5 典型非周期信号的频谱
X
主要内容
本节将讨论如下信号的频谱密度函数 矩形脉冲 单边指数信号 直流信号 符号函数
重点 矩形脉冲的频谱密度函数 难点 不满足绝对可积条件信号的频谱
X
一.矩形脉冲信号
f t
E 2 0 2
F
2 2
Ee
j
t
dt
E
f
(t
)
第三节瞬变非周期信号与连续频谱

δ(t)。 δ函数也称为单位脉冲函数。
从函数值极限的角度看:
(t 0) (t ) 0(t 0)
从面积(通常也称其为δ函数的强度)的角度看:
(t )dt lim S (t )dt 1
0
(2)δ函数的性质
A、乘积特性
x(t ) (t ) x(0) (t )
C、δ函数为偶函数,即:
(t ) (t )
D、 δ函数与其它函数的卷积
x(t ) (t ) x(t )
x(t ) (t t 0 ) x(t t 0 )
(3)δ函数的频谱
将δ(t)进行傅立叶变换:
( ) (t )e
jt
z (t ) cos 0 t
因此被矩形窗函数截断的余弦函数可表示为:
x(t ) w(t ) z (t ) cos 0 t (T t T ) 0其它
其中:
W ( ) 2T sin c(T )
由于余弦函数不满足绝对可积条件,因此不 能用傅立叶变换公式直接计算它的频谱密度函数, 根据欧拉公式可知:
其中:
幅度频谱为:
X ( ) 1 a2 2
相位频谱为:
( ) arctg
a
|X(ω)|
0
ω
Φ(ω)
2
ω
2
例1-3
求被矩形窗函数截断的余弦函数的傅立叶变
换
解: 根据图可将矩形窗函数和余弦函数分别表示
为:
1(T t T ) w(t ) 0其它
T称为窗宽
w(t)的频谱为:
W ( ) w(t )e jwt dt
从函数值极限的角度看:
(t 0) (t ) 0(t 0)
从面积(通常也称其为δ函数的强度)的角度看:
(t )dt lim S (t )dt 1
0
(2)δ函数的性质
A、乘积特性
x(t ) (t ) x(0) (t )
C、δ函数为偶函数,即:
(t ) (t )
D、 δ函数与其它函数的卷积
x(t ) (t ) x(t )
x(t ) (t t 0 ) x(t t 0 )
(3)δ函数的频谱
将δ(t)进行傅立叶变换:
( ) (t )e
jt
z (t ) cos 0 t
因此被矩形窗函数截断的余弦函数可表示为:
x(t ) w(t ) z (t ) cos 0 t (T t T ) 0其它
其中:
W ( ) 2T sin c(T )
由于余弦函数不满足绝对可积条件,因此不 能用傅立叶变换公式直接计算它的频谱密度函数, 根据欧拉公式可知:
其中:
幅度频谱为:
X ( ) 1 a2 2
相位频谱为:
( ) arctg
a
|X(ω)|
0
ω
Φ(ω)
2
ω
2
例1-3
求被矩形窗函数截断的余弦函数的傅立叶变
换
解: 根据图可将矩形窗函数和余弦函数分别表示
为:
1(T t T ) w(t ) 0其它
T称为窗宽
w(t)的频谱为:
W ( ) w(t )e jwt dt
§3-3 非周期信号的频谱分析
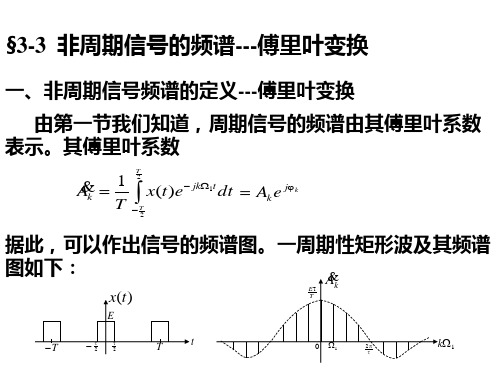
x(t)
E
T
2
2
T
t
x(t)
E
T
2
2
T
t
x(t)
E
2
2
t
TA k E
0 1
2
k1
TA k E
0 1
2
k1
TA k E
0
2
对应的傅里叶级数展开式
x(t)
Ak e jk1t
k
TAk e jk1t
我们将X(jΩ)表示非周期信号的频谱,即是傅里叶正变 换
X ( j) x(t)e jt dt
式
x(t)
1
X ( j)e jt d
2
即是傅里叶反变换。上两式称作傅里叶变换对,常表示为
x(t) FT X ( j) ℱ x(t)
x(t) ℱ -1 X ( j)
k
1 T
1 2
TAk e jk1t
k
2 T
当T→∞的时候,
lim x(t)
T
1 2
TAk e
k
jk1t
2 T
lim
T
1 2
TAk e
k
jk1t
1
1
X ( j)e jt d
2
T
E
T
2
2
T
t
0 1
2
k1
x(t)
E
T
2
2
非周期信号的频谱

(2) 若f(t)为t的奇函数,即f(-t)=-f(t),则f(t)的频 谱函数F(jω)为ω的虚函数,且为ω的奇函数。
与周期信号类似,也可将非周期信号的傅里叶变
换表示式改写成三角函数的形式,即
.
6
f(t)21
F(j)ejtd
21
F(j)ej[t()]d
2 1 F (j)co ts [()d ]
2
0
2
t
实偶
4
2
0
2
4
实偶
图 3.4-1 门函数及其频谱
一般而言,信号的频谱函数需要用幅度谱 F( j)和相位
谱 ( )两个图形才能将它完全表示出来。但如果频谱
函数是实函数或虚函数,那么只用一条曲线即可。
F(j) 为负代表相位为 ,
0
.
F(为j正) 代表相位为 。
11
由图可见,第一个零值的角频率为 2 (频率 1 )。
为了描述非周期信号的频谱特性,引入频谱密度的 概念。
令
F(j)T l i m 1F /n TT l i m FnT
称 F(j)为频谱密.度函数。
2
如何求频谱密度函数? F(j)T l i m 1F /n TT l i m FnT
由式
f(t) Fnejnt
n
,Fn
1 T
T
2 T
2
f(t)ej ntd t可得
可知
'(t)ejtd tdejt j
dt t 0
即 ℱ 'tj
同理可得 ℱ [(n)(t). ](j)n
23
例3.4-6 求单位直流信号的频谱
f(t)1 - t
显然,该信号不满足绝对可积条件,但其傅里叶变换
非周期信号的频谱

jnω1t
1 T2 − jnω1t Fn = F (nω1 ) = ∫−T f (t )e dt T 2
i
3.4 非周期信号的频谱
当 T → ∞ 时,
周期信号 离散谱
非周期信号 连续谱
表示频谱就不合适了, 再用 F ( nω1 ) 表示频谱就不合适了,虽然各频 谱幅度无限小,但相对大小仍有区别, 谱幅度无限小,但相对大小仍有区别,所以我们 在这里引入频谱密度函数。 在这里引入频谱密度函数。 频谱密度函数
jωt
f ( t ) ↔ F ( jω )
3.4 非周期信号的频谱 三、典型信号的傅里叶变换
1.单位冲激信号的频谱 1.单位冲激信号的频谱
f (t ) = δ ( t )
F ( jω ) = ∫ δ ( t ) e− jωt dt = 1
−∞ ∞
即
δ (t ) ↔ 1
3.4 非周期信号的频谱
单位冲激信号的频谱图 单位冲激信号的频谱图 可见, 的频谱是常数1 可见 , 冲激函数 δ(t) 的频谱是常数 1 。 也就 是说, 中包含了所有的频率分量, 是说 , δ(t) 中包含了所有的频率分量 , 而各频率 分量的频谱密度都相等。 显然, 分量的频谱密度都相等 。 显然 , 信号 δ(t) 实际上 是无法实现的。 是无法实现的。
Fn T jnω1t f (t ) = lim fT (t ) = lim ∑ e T →∞ n =−∞ T
当 T → ∞ 时, Fn T = F ( jω )
i
∞
i
nω1 → ω
n =−∞
1 1 1 = ω1 → dω T 2π 2π
T →∞
lim
∑ →∫
jω t
∞
非周期信号

第一章 信号及其描述
因此: ① 离散谱就变成了连续谱。 ② 求和运算则可用积分运算代替。
∞
x (t ) =
∫
−∞
ω0 ( 2π
∫
∞
−∞
x ( t ) e − jn ω 0 t dt ) e
jn ω 0 t
因为 1/T=ω0/2π当 T→∞,ω0=△ω→dω,n ω0 →ω ∞ 1 ∞ − jω t jω t x (t ) = ∫ ( x ( t ) e dt ) e dω ∫ −∞ − ∞ 2π 令:
∫
∞
−∞ ∞
x ( t ) cos 2 π ftdt x ( t ) sin 2 π ftdt
∫
−∞
① 若:x(t) 为实的偶函数,则其富氏变换 x(f) 为:
R e x ( f ) = 2 ∫ x ( t ) cos 2π ftdt
0
∞
I m x( f ) = 0
故:x(f) 是 f 的偶函数又是实函数。即 Rex(f) = x(-f)
设复数 Z=a+bi.当 b≠0 时.z 就叫虚数.a=0,b≠0 时 z 叫纯虚数。
第一章 信号及其描述
作用与定义: 作用与定义:
∞ −∞
x( f ) =
∫
x ( t ) e − j 2 π ft dt = R e x ( f ) − jI m x ( f )
Re x( f ) = Im x( f ) =
1 x (ω ) = 2π
∫
∞
−∞
x ( t ) e − j ω t dt
jω t
FT
x (t ) =
∫
∞
−∞
x (ω ) e
dω
IFT
非周期信号的频谱——傅里叶变换

(3.2-2)
•
式中, |F(ω)|是振幅谱密度函数, 简
称振幅谱; φ(ω)是相位谱密度函数, 简
称相位谱。 一般把式(3.2-1)与式(3.2-2)叫
做傅里叶变换对, 其中式(3.2-1)为傅里
叶变换, 式(3.2-2)为傅里叶反变换。 傅
里叶变换对关系也常用下述符号表示
F( j) F[ f (t)]
信号与系统
非周期信号的频谱——傅里叶变换
• 1.1 从傅里叶级数到傅里叶变换
•
若将非周期信号看作是周期信号
T→∞的极限情况, 非周期信号就可以表
示为
lim
T
fT (t)
f
(t)
• 以周期矩形脉冲为例, 当T→∞时, 周期信号就变成单脉冲信号的非周期信 号。 随着T的增大, 离散谱线间隔ω0就 变窄; 当T→∞, ω0→0, |Fn|→0时, 离 散谱就变成了连续谱。 虽然|Fn|→0, 但 其频谱分布规律依然存在, 它们之间的 相对值仍有差别。 为了表明这种振幅、 相位随频率变化的相对关系, 我们引入 频谱密度函数。
fT (t)
n
1 T
f
T
(
t
)e
jn0t
dt
e
jn
0t
fT (t)
n
0 2
fT (t)e jn0tdte jn0t
f (t)
1
2
fT (t)e j tdt e j td
f (t) 1 F ( j )e j td
2
(3.2-1)
F ( j ) F ( ) e j ( )
• 已知周期函数的傅里叶级
数为
fT (t)
非周期信号的频谱

F(j)称为 f(t) 的傅里叶变换或频谱密度函数,简称频谱;
f(t) 称为F(j) 的傅里叶反变换或原函数。
也可简记为: F ( j )
f (t)
f (t)
1 F ( j)
或者: f (t ) F ( j )
频谱密度函数
F ( j ) 一般为复函数,可写为
F ( j) F ( j) ej () F ( ) e j ()
0,
2
A e j tdt
2
A e j t 2
j
2A sin 2
A Sa( )
2
2
t
2
t
2
8.矩形脉冲信号的频谱
f (t ) A
2π
F( j)
A
t 2 0 2
0 2π 4π
Ag (t)
A
Sa( )
2
傅里叶变换对 F ( j ) f ( t ) e j t d t
T
Fn
2Fn 1
Fn f1
T
2 T
f ( t ) e j n 1t d t
2
其中, Fn 或 Fn 表示单位频带上的频谱值,即频谱密度。
1
f1
对上式取极限 T ,各变量将相应改为 T
虽然 记作
Fn 0
F ( j)
,但
T
F
n 趋于一有限函数
1
2
T
d
n 1 n
F ( j )
et t 0
f (t) e t t 0
为 0的实数
F ( j) 0 eate jtdt eate jtdt j
2
0
2 a2
F (j) 2 2 a2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R() ftcotsdt X() ftsi ntdt
F(j) R2()X2()
()arctaXn() R()
是 的偶函数。
是 的奇函数。
结论: 在f(t)
(1) 若f(t)为t的偶函数,即f(t)=f(-t),则f(t)的频谱 函数F(jω)为ω的实函数, 且为ω的偶函数。
(2) 若f(t)为t的奇函数,即f(-t)=-f(t),则f(t)的频 谱函数F(jω)为ω的虚函数,且为ω的奇函数。
f(t)21F(j)co s[t()]d 10F(j)co s[t()]d
上式表明,非周期信号可看作是由不同频率的余弦“分 量”所组成,它包含了频率从零到无限大的一切频率 “分
量”。由式可见,Fj d2Fjdf 相当于各
“分所量以”信的号振的幅频,谱它不是能无再穷用小幅量度。表示,而改用密度函 数来表示。类似于物质的密度是单位体积的质量,函数
图 3.4-3 单边指数函数 e t t 0
例 3.4-3 求下图所示双边指数信号的频谱函数。
f1 (t)
1
et
e-t
0
t
解:上图所示的信号可表示为:
或者写为
f(t)et , 0 1
et , f1(t)et ,
t 0 t 0
将 f (t) 代入到式 1
F(j)f(t)ejtdt ,
可得其频谱函数为:
Fj 可看作是单位频率的振幅,称 Fj为频谱密度
函数。
二、 典型信号的傅里叶变换 例3.4-1 下图所示为门函数(或称矩形脉冲),用符号
g (t ) 表示,其宽度为 ,幅度为 1。求其频谱函数。
g t
1
2
0
2
t
解: 如图所示的门函数可表示为 其频谱函数为
g
t
1 ,
0
,
t
2
t
2
F(j ) f(t)ejtdt
e e dt t jt 0
1
j
0
这是一复函数,将它分为模和相角两部分:
F(j ) 1 j
1 2
ejarctan) (
2
F(j)ej()
幅度谱和相位谱分别为:
F(j) 1 2 2
频谱图如下图所示:
Fj
1/
()arctan)(
() / 2
0
(a) 振幅频谱
0
- / 2
(b) 相位频谱
F 1 (j
)0e te jtd t e te jtdt
0
11
j j
2 2 2
f1 (t)
1
et
e-t
0
t
实偶
其频谱图如下所示 :
F1(j) 2/
0
F1(j)222
实偶
例3.4-4 求下图所示信号的频谱函数。
f2 (t)
1
e-t
0
t
-et
-1
解: 上图所示的信号可写为 :
et, f2(t)et,
T
FnT
2 T
f(t)ejntdt
2
.
f(t)
n
FnTejnt
1 T
当周期 T 趋近于无限大时, 趋近于无穷小,取其
为
d
,而
1
T 2
将趋近于
0 时,它是离散值,当
d
2
,n 是变量,当
趋近于无限小时,它
就成为连续变量,取为 ,求和符号改为积分。
T
于是当 T时,式
成为
FnT
2 T
f(t)ejntdt
Fj
(时域越窄,频域越宽)
4
2
0
2
4
例3.4-2 求下图所示的单边指数函数的频谱函数.
ett
1
0
t
图 3.4-2 单边指数函数 e t t 0
解: 将单边指数函数的表示式 et t 代入到式
F (j ) f(t)ejtdt中得:
F ( j )
f (t )e jt dt
复习
• 1、周期信号的频谱 • 2、周期信号频谱的特点 • 3、周期信号的功率谱
3.4 非周期信号的频谱
一、傅里叶变换
前已指出,当周期趋于无限大时,相邻谱线的间隔 趋近于无穷小,从而信号的频谱密集成为连续频谱。同 时,各频率分量的幅度也都趋近于无穷小,不过,这些 无穷小量之间仍保持一定的比例关系。
为了描述非周期信号的频谱特性,引入频谱密度的 概念。
令
F(j)T l i m 1F /n TT l i m FnT
称 F( j)为频谱密度函数。
如何求频谱密度函数? F(j)T l i m 1F /n TT l i m FnT
由式 f(t) Fnejnt
n
,Fn
1 T
T
2 T
2
f(t)ejntdt可得
2
f(t)
n
FnTejnt
1 T
F (j ) T l i F m n T f(t)e j td t(1 )
def 1 f(t)
F (j
)ejtd(2)
2
(1)式称为函数 f (t) 的傅里叶变换 。 (2)式称为函数 F( j) 的傅里叶逆变换。
F(j)称为 f (t) 的频谱密度函数或频谱函数.
221ejtdtej2 j ej 2
2jsin
2
j
sin
2
2
S(a)2gຫໍສະໝຸດ tSa 2
g t
1
F jSa 2
2
0
2
t
实偶
4
2
0
2
4
实偶
图 3.4-1 门函数及其频谱
一般而言,信号的频谱函数需要用幅度谱 F( j) 和相位
谱()两个图形才能将它完全表示出来。但如果频谱
函数是实函数或虚函数,那么只用一条曲线即可。
f (t) 称为 F(j) 的原函数。
简记为 f(t) F(j)
ℱftF j
与周期信号的傅里叶级数相类似,在f(t)是实函
数时, F(ω)、φ(ω)与R(ω)、 X(ω)相互之间存在下列
关系:
F (j) F (j)e j( ) R () j( X )
F(j) f(t)ejtdt
f(t)costdtj ftsin tdt
F( j) 为负代表相位为 , 0
F(为j正) 代表相位为 。
由图可见,第一个零值的角频率为 2 (频率 1 )。
当脉冲宽度减小时,第一个零值频率也相应增高。 对于矩形脉冲,常取从零频率到第一个零值频率 ( 1 )
之间的频段为信号的频带宽度。
这样,门函数的带宽 f 1 ,脉冲宽度越窄,
其占有的频带越宽。
与周期信号类似,也可将非周期信号的傅里叶 变换表示式改写成三角函数的形式,即
f(t)21
F(j)ejtd
21
F(j)ej[t()]d
2 1 F (j)co ts [()d ]
j2 1 F (j)s i n t [( )d ]
0
ft2 1 F (j)co t s( [)d ]
t0
(其中 0)
t0
F(j 2
) f(t)ejtdt
0 etejtdt e e dt t jt
0
1 1
j j
2
j
