名校2014届高三12月月考数学试题分类汇编1:集合
2014届高三年级12月月考 数学试题
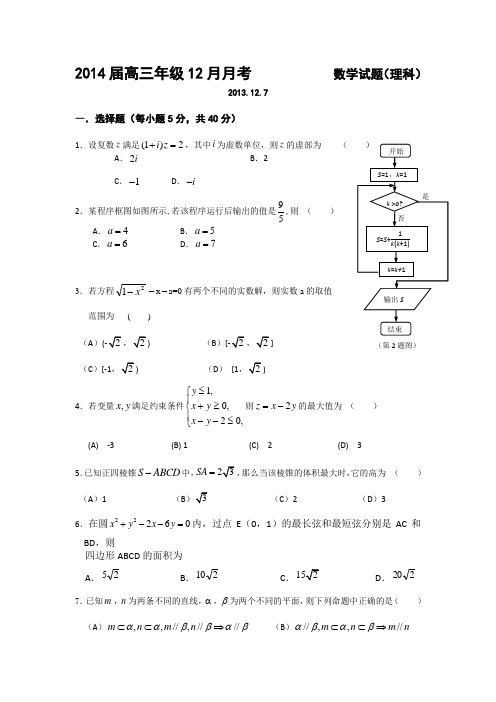
2014届高三年级12月月考 数学试题(理科)2013.12.7一.选择题(每小题5分,共40分)1.设复数z 满足(1)2i z +=,其中i 为虚数单位,则z 的虚部为 (A .2iB .2C .1-D .i -2.某程序框图如图所示,若该程序运行后输出的值是59,则 ( ) A .4=a B .5=aC .6=aD .7=a3.若方程21x--x -a=0有两个不同的实数解,则实数a 的取值范围为 ( )(A ) (B )] (C )[-1 (D ) [1)4.若变量,x y 满足约束条件1,0,20,y x y x y ≤⎧⎪+≥⎨⎪--≤⎩则2z x y =-的最大值为 ( )(A) -3 (B) 1 (C) 2 (D) 35.已知正四棱锥S ABCD -中,SA =,那么当该棱锥的体积最大时,它的高为 ( )(A )1 (B (C )2 (D )3 6.在圆22260x y x y +--=内,过点E (0,1)的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为A .25B .210C .D .2207.已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( ) (A ),,//,////m n m n ααββαβ⊂⊂⇒ (B )//,,//m n m n αβαβ⊂⊂⇒(第2题图)(C ),//m m n n αα⊥⊥⇒ (D )//,m n n m αα⊥⇒⊥8.已知圆O 的半径为1,PA 、PB 为该圆的两条切线,A 、B 为两切点,那么PA PB ∙的最小值为( )(A) 3-+(B)3-(C) 4-+ (D)4-+二.填空题(每小题5分,共30分)9.若函数()f x ax b =-的零点是1, 则2()g x bx ax =-的零点是 .10.例6. 某几何体的三视图如图所示,则它的体积为______11.直线2cos 1ρθ=与圆2cos ρθ=相交的弦长为 .12.设f(x)是定义在R 上的奇函数,且当x ≤0时,f(x)=-x 2,若对任意的x ∈[t ,t +2],不等式f(x+t) ≥2f(x)恒成立,则实数t 的取值范围为__ 13.在直角坐标系xOy 中,M 是曲线1C :1,12x t y t =+⎧⎨=-⎩(t 为参数)上任意一点,N 是曲线2C :1cos ,sin x y θθ=-+⎧⎨=⎩(θ为参数)上任意一点,则MN 的最小值为 .14.已知关于x 的方程x 3+ax 2+bx+c=0有三个实数根可作为一个椭圆、一个双曲线、一个抛物线的离心率(抛物线的离心率为1),则1a 1+-b 的取值范围为 三.解答题(共80分)15.(本小题共13分)已知函数2()22sin f x x x =-. (Ⅰ)求函数()f x 的最大值; (II )求函数()f x 的零点的集合。
四川省各地2014届高三最新模拟试题分类汇编1:集合

四川省各地2014届高三最新模拟试题分类汇编集合一、选择题1、(绵阳市南山中学2014届高三上学期12月月考)已知全集U R =.集合{}3|<=x x A ,{}0log |2<=x x B ,则=⋂B A ( )A. {}13x x <<B.{}1<x xC. {}3x x <D. {}10<<x x 答案:D2、(雅安中学2014届高三上学期12月月考)设集合M={x|x 2≤4),N={x|log 2 x ≥1},则M ∩N 等于( ) A .[﹣2,2]B . {2}C . [2,+∞)D . [﹣2,+∞) 答案:B3、(成都七中2014届高三上期中考试)已知全集U=R ,集合A={}13>x x ,B={}0log 2>x x ,则A ∪B=( )A .{}0>x xB .{}1>x xC .{}10<<x xD .{}0<x x答案:A 4、(成都高新区2014届高三10月统一检测)若集合{2,1,0,1,2}A =--,集合{}3,2,0,1=B ,则=B AA.{1,2,3}B.{0,1,2}C.{0,1,2,3}D.{1,0,1,2,3}- 答案:B5、(成都石室中学2014届高三上学期期中)设全集U R =,集合{}{}2,05A x x B x x =≥=≤<,则集合()U C A B =( )A. {}02x x <<B. {}02x x <≤C. {}02x x ≤<D. {}02x x ≤≤答案:C6、(成都市2014届高三上学期摸底)设集合A={l ,2},B={2,4),则AUB=A .{1}B .{4}C .{l,4}D .{1,2,4}答案:D7、(树德中学高2014届高三上学期期中)已知全集{}0,1,2,3,4,5,6,7,8,9U =,若 {}0,1,3,5,8A =, {}2,4,5,6,8B =时,则()()U U A B ⋂=痧A .{}5,8B .{}7,9C .{}0,1,3D .{}2,4,68、(成都外国语学校2014届高三11月月考)若全集U ={}x ∈R|x 2≤4,则集合A ={}x ∈R||x +1|≤1的补集∁U A 为(C)A .{}x ∈R|0<x <2B .{}x ∈R|0≤x <2C .{}x ∈R|0<x ≤2D .{}x ∈R|0≤x ≤2答案:C1.9、(达州市普通高中2014届高三第一次诊断检测)2.已知全集U R =,集合2{3},{,5}A x Z y x B y y x x =∈=-==≤,则A B ⋂等于 A .[]3,5 B .[)3,5 C .{4,5} D . {3,4,5}答案:D10、(德阳中学2014届高三“零诊”考试)1.若集合}0|||(>+=x x x A , }065|{2≥+-=x x x B ,则=B A ( )A . }32|{≤≤x xB .20|{≤≤x x 或}3≥xC . 20|{≤<x x 或}3≥xD .}3|{≥x x 答案:C11、(乐山市第一中学2014届高三10月月考)若集合A ={-1,1},B ={0,2},则集合{z |z =x +y ,x ∈A ,y ∈学科网B }中的元素的个数为( )A .5B .4C .3D .2答案:C12、(泸州市2014届高三第一次教学质量诊断)已知全集U ={1,2,3,4,5,6,7,8},M ={1,3,5,7},N ={5,6,7},则()U M N ð=A .{5,7}B .{2,4}C .{1,3,5,6,7}D .{2,4,8}答案:D13、(绵阳市高中2014届高三11月第一次诊断性考试)若集合A ={x |1<x <4},集合B ={y |y 2<4},则A ∩B =A 、∅B 、{1,2}C 、(1,2)D 、(1,4)答案:C14、(什邡中学高中2014届高三上学期第二次月考)若集合{}cos ,A y y x x R ==∈,{}ln B x y x ==,则A B =( )A .{}|11x x -≤≤B .{}|0x x ≥C .{}01x x <≤D .∅答案:C15、(资阳市2014届高三上学期第一次诊断性考试)已知集合A ={4,5,6,8},B ={3,5,7,8},则A ∩B =(A ){3,5}(B ){6,8} (C ){5,8}(D ){3,4,5,6,7,8}16、(德阳中学2014届高三“零诊”考试)设集合}{1,2,3,4,5,6,7,8,9S =,集合}{123,,A a a a =,A S ⊆,123,,a a a 满足123a a a <<且326a a -≤,那么满足条件的集合A 的个数为( )A . 76B .78C .83D .84 答案:C17、(乐山第一中学2014届高三10月月考)设集合{}|23,S x x =->{}|8,T x a x a S T R =<<+= ,则a 的取值范围是( ) A.13-<<-a B.13-≤≤-a C.3-≤a 或1-≥a D. 3-<a 或1->a 答案:A。
2014年普通高等学校招生全国统一考试分类汇编1—集合概念及运算(理科) S

B. C. D.
10. 【2014四川高考理第1题】已知集合 ,集合 为整数集,则A B=( )
A. B. C. D.
11. 【2014浙江高考理第1题】设全集 ,集合 ,则 ( )
B. C. D.
12. 【2014重庆高考理第11题】设全集
______.
13. 【2014陕西高考理第1题】已知集合 ,则 ( )
14.【2014大纲高考理第2题】设集合 , ,则 ( )
A. B. C. D.
15.(2014广西)设集合 , ,则 ()
A. B. C. D.
A{0}. B.{0,1}.C.{0,2}.D.{0,1,2}.
4. 【2014高考湖北卷理第3题】设U为全集,A,B是集合,则“存在集合 使得 是“ ”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 【2014高考江苏卷第1题】已知集合 , ,则 .
2014年普通高等学校招生全国统一考试分类汇编(1)
集合概念及运算
1.【2014广东 理科卷】已知集合 , ,则
A. B. C. D.
2.【2014广东 理科卷】设集合 ,那么集合A中满足条件“ ”的元素个数为
A.60B.90C.120D.130
3.【2014高考北京理】已知集合A={x| },B={0,1,2},则A B=( )
6.【2014辽宁高考理第1题】已知全集 ,则集合1高考理第1题】已知集合 ,则 ( )
A. B. C.. D.
8. 【2014全国2高考理第1题】设集合M={0,1,2},N= ,则 =( )
【备考2015】全国名校2014高考数学试题分类汇编(12月 第一期)A1 集合及其运算(含解析)

A1 集合及其运算【数学理卷·2015届辽宁省沈阳二中高三上学期期中考试(201411)】2. 已知集合2{|}M x x x =>,4{|,}2xN y y x M ==∈,则M N = ( )A .{x |0<x <12} B.{x |12<x <1} C.{x |0<x <1} D.{x |1<x <2}【思路点拨】利用一元二次不等式的解法和指数函数的性质可化简集合M ,N .再利用交集的运算即可得出.【数学理卷·2015届湖南省岳阳一中高三上学期第三次月考(201411)】11. 已知集合{}{}()R |,|12,R A x x a B x x AB =<=<<=且ð,则实数a 的取值范围是 .【知识点】补集、并集的运算.A1 【答案】【解析】2a ≥ 解析:{}R 12B x x =≤≥或ð,且()R R AB =ð,可得2a ≥,故答案为2a ≥。
【思路点拨】先根据已知条件求出B 的补集,再根据()R R A B =ð可求结果。
【数学理卷·2015届河南省实验中学高三上学期期中考试(201411)】1.已知集合{||2,}A x x x R =≤∈,{4,}B x x Z =∈,则A B ⋂=( )A.(0,2)B.[0,2]C.(0,2]D.{0,1,2}【知识点】集合及其运算A1【答案解析】D A={22x x -≤≤},B={016,x x x z ≤≤∈},则A B ⋂={0,1,2}故选D.【思路点拨】先求出A,B 再求结果。
【数学理卷·2015届河北省衡水中学高三上学期期中考试(201411)】1.设集合{|1},{|1}A x x B x x =>-=≥,则“x A ∈且x B ∉”成立的充要条件是( )A .11x -<≤B .1x ≤C .1x >-D .11x -<<【知识点】集合.A1【答案】【解析】D 解析:由充要条件的意义可知,x 只属于A 集合不属于B 集合,所以D 为正确选项.【思路点拨】根据题意可直接求出所应表示的部分【数学理卷·2015届江西省赣州市十二县(市)高三上学期期中联考(201411)】11.设集合}1,0,1{-=M ,},{2a a N =,若N N M =⋂,则a 的值是 .【知识点】交集及其运算.A1【答案】【解析】-1 解析:因为集合}1,0,1{-=M ,},{2a a N =,若N N M =⋂, 又a 2≥0,∴当a 2=0时,a=0,此时N={0,0},不符合集合元素的互异性,故a≠0,当a 2=1时,a=±1,a=1时,N={1,1},不符合集合元素的互异性,故a≠1,a=﹣1,此时N={﹣1,1},故a=﹣1.故答案为:﹣1。
辽宁版02期 2014届高三名校数学理试题分省分项汇编专题01 集合与常用逻辑用语 含解析

一.基础题组1.【辽宁省五校协作体2014届高三摸底考试数学(理)】设集合{|13},{|12},A x x B x x x A B =<<=<->或则为()A .{|11}x x x <->或B .{|12}x x x <->或C .{|23}x x <<D .R2.【辽宁省抚顺市六校联合体2014届高三上学期期中考试理】已知集合}{|3A x x =<,}{2|log0B x x =>则A B =( )A.}{|13x x <<B 。
}{|3x x <C.}{|1x x >D.∅3。
【辽宁省沈阳二中2014届高三上学期期中考试理】已知全集为R ,集合112xA x ⎧⎫⎪⎪⎛⎫=≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,{}2|680B x x x =-+≤,则R A C B =()A.{}|0x x ≤B.{}|24x x ≤≤C. {}|024x x x <≤≥或D. {}|024x x x ≤<>或4。
【辽宁省五校协作体2014届高三摸底考试数学(理)】已知命题3:2,80,P x x ∀>->那么⌝P 是() A . 32,80x x ∀≤-≤ B .32,80x x∃>-≤ C .32,80x x ∀>-≤D .32,80x x∃≤-≤5。
【辽宁省铁岭市第一高级中学2013-2014学年高三上学期期中考试试题理】设集合}{10,1,1x A x B x x x ⎧-⎫=≤=≤⎨⎬+⎭⎩则“x A ∈”是“x B ∈”的()A.充要条件B.必要不充分条件 C 。
充分不必要条件 D.既不充分也不必要条件二.能力题组1.【辽宁省铁岭市第一高级中学2013-2014学年高三上学期期中考试试题理】已知全集U=R ,集合{1lg1M x y x ⎫==⎬-⎭,}{sin 2xN y y ==,则()U C M N =()A. (]1,2B. 1,22⎡⎤⎢⎥⎣⎦C 。
2014年全国高考理科数学试题分类汇编1集合(有答案)

2014年全国高考理科数学试题分类汇编1:集合一、选择题1已知全集{}1,2,3,4U =,集合{}=12A ,,{}=23B ,,则()=U A B ð( ) A.{}134,, B.{}34, C. {}3 D. {}4 【答案】D2已知集合{}{}4|0log 1,|2A x x B x x A B =<<=≤=,则A.()01,B.(]02,C.()1,2D.(]12, 【答案】D3已知集合A = {x ∈R | |x |≤2}, A = {x ∈R | x ≤1}, 则A B ⋂=(A) (,2]-∞ (B) [1,2] (C) [2,2] (D) [-2,1]【答案】D4设S,T,是R 的两个非空子集,如果存在一个从S 到T 的函数()y f x =满足:(){()|};()i T f x x S ii =∈ 对任意12,,x x S ∈当12x x <时,恒有12()()f x f x <,那么称这两个集合“保序同构”.以下集合对不是“保序同构”的是( )A.*,A N B N ==B.{|13},{|8010}A x x B x x x =-≤≤==-<≤或C.{|01},A x x B R =<<=D.,A Z B Q ==【答案】D5设常数a R ∈,集合{|(1)()0},{|1}A x x x a B x x a =--≥=≥-,若A B R ⋃=,则a 的取值范围为( )(A) (,2)-∞ (B) (,2]-∞ (C) (2,)+∞ (D) [2,)+∞【答案】B.6已知集合A ={0,1,2},则集合B ={},x y x A y A -∈∈中元素的个数是(A) 1 (B) 3 (C)5 (D)9【答案】C7设全集为R , 函数()f x =M , 则C M R 为 (A) [-1,1] (B) (-1,1)(C) ,1][1,)(∞-⋃+∞- (D) ,1)(1,)(∞-⋃+∞-【答案】D8设集合{}{}{}1,2,3,4,5,|,,,A B M x x a b a A b B ====+∈∈则M 中的元素个数为(A)3 (B)4 (C)5 (D)6【答案】B9设集合{|20}A x x =+=,集合2{|40}B x x =-=,则A B =( )(A){2}- (B){2} (C){2,2}- (D)∅【答案】A10已知集合{}{2|20,|A x x x B x x =->=<<,则 ( )A.A∩B=∅B.A∪B=RC.B ⊆AD.A ⊆B【答案】B.11已知全集为R ,集合112x A x ⎧⎫⎪⎪⎛⎫=≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,{}2|680B x x x =-+≤,则R A C B =( ) A.{}|0x x ≤ B.{}|24x x ≤≤C. {}|024x x x ≤<>或D.{}|024x x x <≤≥或【答案】C12已知集合{}{}2|(1)4,,1,0,1,2,3M x x x R N =-<∈=-,则=N M(A){}2,1,0 (B){}2,1,0,1- (C){}3,2,0,1- (D){}3,2,1,0【答案】A13设集合{}2|20,M x x x x =+=∈R ,{}2|20,N x x x x =-=∈R ,则M N =( )A . {}0 B.{}0,2 C.{}2,0- D.{}2,0,2-【答案】D14设集合}043|{},2|{2≤-+=->=x x x T x x S ,则=⋃T S C R )(A.(2,1]-B. ]4,(--∞C. ]1,(-∞D.),1[+∞【答案】C15设整数4n ≥,集合{}1,2,3,,X n =.令集合(){},,|,,,,,S x y z x y z X x y z y z x z x y =∈<<<<<<且三条件恰有一个成立,若(),,x y z 和(),,z w x 都在S 中,则下列选项正确的是( )A . (),,y z w S ∈,(),,x y w S ∉ B.(),,y z w S ∈,(),,x y w S ∈C.(),,y z w S ∉,(),,x y w S ∈D.(),,y z w S ∉,(),,x y w S ∈(一)必做题(9~13题)【答案】B16已知集合A={-1,0,1},B={x |-1≤ x <1},则A∩B= ( )A.{0}B.{-1,0}C.{0,1}D.{-1,0,1}【答案】B17设全集U R =,下列集合运算结果为R 的是( )(A)u Z N ð (B)u N N ð (C)()u u ∅痧 (D){0}u ð【答案】A二、填空题1集合}1,0,1{-共有___________个子集.【答案】8三、解答题2对正整数n ,记{}1,2,3,,m I n =,,m m m P I k I ⎫=∈⎬⎭. (1)求集合7P 中元素的个数; (2)若m P 的子集A 中任意两个元素之和不是..整数的平方,则称A 为“稀疏集”.求n 的最大值,使m P 能分成两人上不相交的稀疏集的并.【答案】。
江苏省名校高三数学 12月月考试题分类汇编15 应用题

江苏省名校2014届高三12月月考数学试题分类汇编应用题1、(江苏省扬州中学2014届高三上学期12月月考)某种商品原来每件售价为25元,年销售8万件.(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到.x 元.公司拟投入21(600)6x -万元作为技改费用,投入50万元作为固定宣传费用,投入15x 万元作为浮动宣传费用.试问:当该商品明年的销售量a 至少应达到多少万件时,才可能使明年的销售收入不低于原收入...与总投入...之和?并求出此时商品的每件定价. 解:(1)设每件定价为x 元,依题意,有25(80.2)2581x x --⨯≥⨯, 整理得26510000x x -+≤,解得2540x ≤≤.∴ 要使销售的总收入不低于原收入,每件定价最多为40元.………7′ (2)依题意,25>x 时,不等式21125850(600)65ax x x ≥⨯++-+有解, 等价于25>x 时,1501165a x x ≥++有解, ()150110306x x x +≥==当且仅当时,等号成立 , 10.2a ∴≥.∴当该商品明年的销售量a 至少应达到10.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元.……14′ 2、(江苏省南京市第一中学2014届高三12月月考)一根水平放置的长方体形枕木的安全负荷与它的宽度a 成正比,与它的厚度d 的平方成正比,与它的长度l 的平方成反比.(Ⅰ)将此枕木翻转90°(即宽度变为厚度),枕木的安全负荷会如何变化?为什么?(设翻转前后枕木的安全负荷分别为21,y y 且翻转前后的比例系数相同都为k )(Ⅱ)现有一根横断面为半圆(已知半圆的半径为R )的木材,用它来截取成长方体形的枕木,其长度为10,问截取枕木的厚度为d 多少时,可使安全负荷y 最大?解:(Ⅰ)安全负荷k l ad k y (221⋅=为正常数)翻转222,90lda k y ⋅=︒后,…2分ady y =21, ∴当a d <<0时,21y y <大. …………4分当 12,0y y d a <<<时,安负荷变小;…………6分当a d =时,21y y =变. ……………7分(II )如图,设截取的宽为a ,厚度为d ,则22222244,)2(R d a R d a=+=+即.1002kad y =)4(10022a R a k -==)4(40032a a R k -= ()2,0(R x ∈)0>k …9分 )34(400322R a k y --=' 令0='y 得: R a 332=当)332,,0(R a ∈时 ,0>'y 函数y 在)332,0(R 上为增函数;当)2,332(R R a ∈时 ,0>'y 函数y 在)2,332(R R 上为减函数;当 R a 332=时,安全负荷y 最大。
云南省部分名校高三数学12月份联考试题 理(含解析)

云南省部分名校2014届高三数学12月份联考试题 理(含解析)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.3.已知某随机变量X 的概率密度函数为P (x )=⎩⎨⎧>≤-0,0,0x e x x ,则随机变量X 落在区间(1,2)内的概率为( )A .e 2+e B .21e e + C .e 2-e D .21e e - 【答案】D 【解析】试题分析:画出概率密度曲线,随机变量X 落在区间(1,2)内的概率相当于1x =和2x =以及密度曲线和0y =围成的阴影部分面积,21x P e dx -=⎰21e e-=. 考点:1、函数的图象;2、定积分的运算和几何意义.4.我校在模块考试中约有1000人参加考试,其数学考试成绩ξ~N(90,a 2)(a >0,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的53,则此次数学考试成绩不低于110分的学生人数约为( )A .600B .400C .300D .2006.设向量=(sin α,)的模为,则cos2α=( ) A .B .C .﹣D .﹣当z 取到最小值时,'z 最小,此时直线'2y x z =--的纵截距最大,故当直线过点(1,2)A 时,'z 取到最小值4-,故yx z )21(4⋅=-的最小值为161. 考点:1、指数幂运算性质;2、线性规划.8.一个几何体的三视图如图所示,其中俯视图是菱形,则该几何体的侧面积为( )A .B .C .D .10.P 是双曲线)0,0(12222>>=-b a by a x 上的点,F 1、F 2是其焦点,且021=⋅PF ,若△F 1PF 2的面积是9,a +b=7,则双曲线的离心率为( )A .B .C .D .11.已知正四棱锥的各棱棱长都为23,则正四棱锥的外接球的表面积为( )A .π12B .π36C .π72D .π108【答案】B【解析】试题分析:在RT ACD ∆中,3AC CD ==,则3AD =,又A C D ∆∽ABC ∆,则有2AC AD AB =⋅,所以=6AB ,3R =,2436S R ππ==.考点:1、正四棱锥的外接球;2、球的表面积.12.设f (x ),g (x )分别是定义在R 上的奇函数和偶函数,当x <0时,0)(')()()('>+x g x f x g x f ,且0)3(=-f ,则不等式0)()(<x g x f 的解集是( )A .(-3,0)∪(3,+∞)B .(-3,0)∪(0,3)C .(-∞,-3)∪(3,+∞)D .(-∞,-3)∪(0,3)第Ⅱ卷(共90分)二、填空题(每题4分,满分16分,将答案填在答题纸上)13.如右图所示的程序框图的输出值]2,1(∈y ,则输入值∈x .【答案】)1,3log []3,1(2-- 【解析】试题分析:程序框图表示的是一个分段函数2log (1),021,0xx x y x -+≥⎧=⎨-<⎩,所以201log (1)2x x ≥⎧⎨<+≤⎩或1212xx -<⎧⎨<-≤⎩,解得{2log 31x x -≤<-,或}13x <≤.. 考点:1、程序框图;2、指数不等式、对数不等式解法.14.P 为抛物线24y x =上任意一点,P 在y 轴上的射影为Q ,点M (4,5),则PQ 与PM 长度之和的最小值为 .116.在ABC ∆中,BC =52,AC =2,ABC ∆的面积为4,则AB 的长为 .【答案】4或【解析】试题分析:由已知1sin 42ABC S BC AC C ∆=⋅⋅⋅=,∴sin C =故c o s C =,在ABC ∆中,当AB =,当cos C =时,AB =4,当cos C =时AB =考点:1、三角形的面积;2、同角三角函数基本关系式;3、余弦定理.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.等比数列{a n }的各项均为正数,且2a 1+3a 2=1,a 23=9a 2a 6.(1)求数列{a n }的通项公式;(2)设31323log log log n n b a a a ⋯=+++,求数列⎩⎨⎧⎭⎬⎫1b n 的前n 项和.18.在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加救援工作,其分布的情况如下表,从这50名队员中随机抽出2人去完成一项特殊任务.(1)求这2人来自同一区域的概率;(2)若这2人来自区域A ,D ,并记来自区域A 队员中的人数为X ,求随机变量X 的分布列及数学期望.所以ξ的分布列是:ξ的数学期望为Eξ=0×+1×+2×=考点:1、古典概型和互斥事件的概率;2、离散型随机变量的分布列和期望.上.BM面ADEF;(I)当点M为EC中点时,求证: //(II)求证:平面BDE丄平面BEC;试题解析:(1)证明 取DE 中点N ,连结,MN AN .在△EDC 中,,M N 分别为,EC ED 的中点,则MN ∥CD ,且12M N C D =.由已知AB ∥CD ,12AB CD =,因此,MN ∥AB ,且M N A B =.所以,四边形ABMN 为平行四边形. 于是,BM ∥AN .又因为AN ⊂平面ADEF ,且BM ⊄平面ADEF ,所以BM ∥平面ADEF ,从而可证.CD E FM(Ⅰ)求椭圆C 的方程;(Ⅱ)如图,动直线:l y kx m =+与椭圆C 有且仅有一个公共点,点,M N 是直线l 上的两点,且l M F ⊥1, l N F ⊥2. 求四边形12F MNF 面积S 的最大值.【答案】(1)22143x y +=;(2)【解析】(2) 将直线l 的方程y kx m =+代入椭圆C 的方程223412x y +=中,得01248)34(222=-+++m kmx x k ,由直线l 与椭圆C 仅有一个公共点知,2222644(43)(412)0k m k m ∆=-+-=,化简得:2243m k =+.设11d F M ==,22d F M ==, (法一)当0k ≠时,设直线l 的倾斜角为θ,则12tan d d MN θ-=⨯,12d d MN k-∴=, 22121212221()221m d d d d S d d k k k --=+==+ m m m m1814322+=+-=, 2243m k =+,∴当0k ≠时,3>m ,3343131=+>+m m ,32<S .当0=k 时,四边形12F MNF是矩形,S =12F MNF 面积S的最大值为21.已知函数()()(),ln x g x f x g x ax x==-. (Ⅰ)求函数()g x 的单调区间;(Ⅱ)若函数()()1,f x +∞在上是减函数,求实数a 的最小值;(Ⅲ)若212,,x x e e ⎡⎤∃∈⎣⎦,使()()12f x f x a '≤+(0>a )成立,求实数a 的取值范围.【答案】(Ⅰ)单调减区间是)e ,1(),1,0(,增区间是),e (+∞.;(Ⅱ)14;(Ⅲ)21124ea ≥-. 【解析】 试题分析:(1)先求'()g x ,解不等式'()0g x >并和定义域求交集,得()g x 的单调递增区间;解不等式'()0g x <并和定义域求交集,得()g x 的单调递减区间;(2)等价于'()0f x ≤在(1,)x ∈+∞时恒成立,即2ln 1()0(ln )x f x a x -'=-≤,故m a x ()0f x '≤,得实数a 的取值范围;(3)由特称量词的含义知,在区间2[,]e e 内存在两个独立变量1,2x x ,使得已知不等式成立,等价于()y f x =2[,]x e e ∈的最小值小于等于'()y f x a =+2[,]x e e ∈的最大值,分别求两个函数的最小值和最大值,建立实数a 的不等式,进而求a 的范围.试题解析:由已知函数)(),(x f x g 的定义域均为),1()1,0(+∞ ,且ax xx x f -=ln )(.()0f x '<,()f x 为减函数;当20(,e )x x ∈时,()0f x '>,()f x 为增函数;所以,min ()f x =00001()ln 4x f x ax x =-≤,20(e,e )x ∈.所以,2001111111ln 44e 244ln e a x x ≥->->-=,与104a <<矛盾,不合题意.综上,得21124ea ≥-. 考点:1、导数在单调性上的应用;2、利用导数求函数的极值和最值.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分22.已知曲线C 的极坐标方程为θθρ2sin cos 4=,直线l 的参数方程为⎩⎨⎧+==ααsin 1cos t y t x ( t 为参数,0≤α<π). (Ⅰ)把曲线C 的极坐标方程化为直角坐标方程,并说明曲线C 的形状;(Ⅱ)若直线l 经过点(1,0),求直线l 被曲线C 截得的线段AB 的长.考点:1、极坐标方程和直角坐标方程的转换;2、直线的参数方程.23.设函数f(x)=|2x-1|+|2x-3|,x∈R(Ⅰ)解不等式f(x)≤5; (Ⅱ)若mx f x g +=)(1)(的定义域为R ,求实数m 的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11、(江苏省兴化市安丰高级中学2014届高三12月月考)设集合 , , ,则 .
答案:
12、(江苏省张家港市后塍高中201பைடு நூலகம்届高三12月月考)设集合A={x|-<x<2},B={x|x2≤1},则A∪B=▲.
答案:{x|-1≤x<2}
江苏省名校2014届高三12月月考数学试题分类汇编
集合
一、填空题
1、(江苏省扬州中学2014届高三上学期12月月考)已知集合 , ,则 ▲.
答案:
2、(江苏省南京市第一中学2014届高三12月月考)已知集合A={-1,0,1},B={x|-1≤x<1},则A∩B=
答案:{-1,0}
3、(江苏省诚贤中学2014届高三12月月考)已知集合 , ,则 =▲.
答案:
4、(江苏省东海县第二中学2014届高三第三次学情调研)
若集合 ,则 ▲.
答案:
5、(江苏省阜宁中学2014届高三第三次调研)若集合 ,则满足条件 有▲个.
答案:3
6、(江苏省灌云高级中学2014届高三第三次学情调研)集合 的所有子集个数为_________.
答案:8
7、(江苏省粱丰高级中学2014届高三12月第三次月考)已知集合 ,若 ,则实数 的值为▲.
答案:1
8、(江苏省如东县掘港高级中学2014届高三第三次调研考试)
已知集合 ,则 .
答案:
9、(江苏省睢宁县菁华高级中学2014届高三12月学情调研)已知全集 ,集合 , ,则 =▲.
答案:{1}
10、(江苏省无锡市洛社高级中学等三校2014届高三12月联考)已知集合U={1,2,3,4},M={1,2},N={2,3},则 =________.
