基于有限元方法的橡胶弹性件设计开发流程
橡胶支座有限元计算
橡胶支座有限元计算橡胶支座是一种常用的结构减震装置，广泛应用于桥梁、建筑物和机械设备等领域。
为了评估橡胶支座在实际工程中的性能，有限元分析是一种常用的方法。
本文将介绍橡胶支座有限元计算的基本原理和步骤，并探讨其在工程中的应用。
橡胶支座是一种由橡胶材料制成的弹性元件，具有良好的减震和隔振效果。
在工程中，它被用于减少结构受力并降低震动传递。
橡胶支座的设计和选型需要考虑多个因素，包括荷载条件、结构要求和橡胶材料的特性等。
有限元分析是一种基于数值计算的方法，可以模拟和分析复杂结构的力学行为。
在橡胶支座的有限元计算中，首先需要建立几何模型。
可以使用专业的有限元软件，如ANSYS或ABAQUS等，通过建立节点、单元和边界条件来描述橡胶支座的几何形状和材料性质。
接下来，需要定义橡胶材料的本构模型。
橡胶材料具有非线性的力学特性，其本构模型可以使用合适的材料模型来描述。
常用的橡胶材料模型有线性弹性模型、非线性弹性模型和超弹性模型等。
在有限元计算中，还需要确定橡胶支座的边界条件。
边界条件包括约束条件和加载条件。
约束条件可以限制橡胶支座的运动自由度，加载条件可以模拟实际工况下的荷载作用。
根据实际情况，可以选择静态加载、动态加载或多次加载等。
完成模型的建立和边界条件的定义后，可以进行有限元计算。
有限元计算可以求解橡胶支座在加载条件下的应力、变形和位移等参数。
通过分析计算结果，可以评估橡胶支座的性能是否满足设计要求，进而优化设计方案。
橡胶支座有限元计算在工程中具有广泛的应用。
例如，在桥梁工程中，可以通过有限元分析评估橡胶支座的减震效果，优化支座的布置和参数，提高桥梁的抗震能力。
在建筑物工程中，可以通过有限元计算分析橡胶支座的变形和位移，评估其对结构的影响，确保结构的安全性。
除了在新建工程中的应用，橡胶支座有限元计算还可以用于现有结构的评估和改造。
通过有限元分析，可以检测结构是否存在问题，如变形过大或应力集中等，为结构的加固和修复提供依据。
橡胶密封制品的有限元模拟与结构优化
2、橡胶制品有限元分析具体案 例分析
(1)轮胎分析：通过有限元分析，可以对轮胎的力学性能进行精确预测，从 而优化其结构设计，提高轮胎的使用性能和安全性。例如，对轮胎进行静力学分 析，可确定轮胎在不同工况下的变形和应力分布情况，避免轮胎在极端工况下出 现损坏或失稳现象。
(2)传动带分析：传动带是机械系统中重要的元件之一，其性能直接影响到 整个系统的稳定性和效率。通过有限元分析，可以对其传动力、传动效率、振动 等性能进行评估，进而优化传动带的设计和生产工艺。例如，对传动带进行动力 学分析，可确定其在不同转速和负载下的振动和疲劳寿命，提高传动系统的稳定 性和效率。
三、橡胶动态性能有限元分析的 未来展望
随着科技的不断发展，有限元分析在橡胶动态性能研究中的应用将更加广泛。 新的算法和计算能力的提升将使得对橡胶制品的动态性能进行更精细的模拟成为 可能。同时，随着材料科学和实验技术的发展，将为有限元模拟提供更准确的材 料模型和边界条件，从而进一步提高模拟的准确性。
橡胶密封制品的有限元模拟与 结构优化
基本内容
橡胶密封制品在工业和日常生活中应用广泛，如汽车、航空航天、电子产品 等领域。它们起着至关重要的作用，不仅可以防止气体和液体的泄漏，还可以防 止灰尘和污垢的侵入。为了提高橡胶密封制品的性能和可靠性，有限元模拟和结 构优化成为越来越重要的工具。
有限元模拟是利用数学方法模拟真实物理系统的过程，以获得系统在不同条 件下的行为和性能。在橡胶密封制品的有限元模拟中，通常选用橡胶材料属性， 如弹性模量、泊松比、剪切模量等，来描述其力学行为。同时，有限元模拟可以 预测和优化橡胶密封制品的结构，以获得最佳的性能。
结论：
有限元数值模拟已成为工程设计和科学研究的重要工具，对于橡胶制品的动 态性能分析具有特别的价值。通过对橡胶动态性能进行有限元模拟，我们可以预 测制品在实际工作环境下的行为，优化设计以改善其性能，并提高产品的可靠性 和使用寿命。
有限元在车辆橡胶元件中的应用
研究开发弹性体,20100825,20(4):34~38CH INAELASTOMERICS收稿日期63作者简介韩智慧(),女,山东省岛人,硕士,主要研究方向为减震系统及橡胶减震件的开发。
有限元在车辆橡胶元件中的应用韩智慧,万里翔,何宇林,曾力(西南交通大学机械学院,四川成都610031)摘要:分别利用闭型方程式与有限元对粘合圆柱橡胶块进行刚度分析对比;利用有限元与试验对3种不同汽车橡胶减震件进行分析对比,体现了有限元法在此设计领域中的可行性与优越性。
关键词:有限元;橡胶元件;刚度中图分类号:TQ 336.4+2文献标识码:A文章编号:10053174(2010)04003405橡胶减震件在汽车上应用非常广泛而且其品种繁多,例如各种衬套、发动机悬置,推力杆橡胶关节等等,但是由于橡胶材料的超强非线性及元件的复杂结构,若仅仅使用有限几个闭型分析方程式是满足不了设计要求的。
随着非线性有限元分析软件的不断发展与日臻完善,其已经可以在汽车橡胶减震元件中得到广泛的应用,成为工程技术人员解决设计分析工作的有效途径。
1粘合圆柱橡胶块的刚度分析对一种结构十分简单而且经典的结构粘合圆柱形橡胶块(结构如图1),通过闭型方程式与有限元的计算对其刚度进行分析并对结果进行比较。
图1粘合圆柱形橡胶块三维模型1.1利用闭型方程式求解1.1.1本构方程橡胶类各向同性不可压缩超弹性材料,文献[1]得其本构方程:e=-P +2W I 1B-W I 2B -1式中:I 1、I 2为Cauch Green 左张量B 的前2个基本不变量,e为高氏应力张量,角标e 表示弹性分析;W(I 1、I 2)是未变形物体单位体积的应变能密度。
本研究中W 的形式为:W =C 10(I 1-3)+C 01(I 2-3)+C 11(I 1-3)(I 2-3)+C 20(I 1-3)2+C 30(I 1-3)3式中由5个常量组成的集合{C 10,C 01,C 11,C 20,C 30}是材料的特性参数,这些特性参数的数值是从单轴和多轴应力松弛数据中得到的,本研究中C 10=100.8kPa,C 01=161.2kPa,C 11=1.338kPa,C 20=0.6206kPa,C 30= 6.206kPa 。
轨道车辆橡胶弹性元件设计计算方法
轨道车辆橡胶弹性元件设计计算方法轨道车辆的安全运行极大的取决于橡胶弹性元件的正确设计，在轨道车辆传动系统中，橡胶弹性元件主要由驱动锥形和传动轮构成，为了满足轨道车辆的传动性能，驱动锥形和传动轮非常脆弱，一旦发生磨损，机械性能将会急剧下降，所以，在整个轨道车辆系统设计过程中，进行合理设计计算是必要的。
首先，在设计计算过程中，首先要考虑受力情况，分析轨道车辆的受力特性，包括轨道车辆的人员载重、运行情况等，以及不同的路段所带来的力学状态，包括路段的斜度、转弯等。
其次，考虑到橡胶弹性元件在轨道车辆系统中所处的惯性位置，考虑轨道车辆在不同速度下弯曲运动的情况，以及考虑通过不同惯性力和静态载荷状态下各个方向上驱动部件和传动部件之间的反力情况，以确定出受力情况和使用要求。
最后，对橡胶弹性元件设计计算的具体实施过程，要根据弹性元件的本质特性和设计要求，采用有限元分析方法，根据橡胶弹性元件的结构、材料性能等参数，结合运行状态下的受力情况，可以得到橡胶弹性元件的具体参数，以及计算出能够满足设计要求下的力学状态，从而进行合理的橡胶弹性元件设计计算。
在完成上述的设计计算过程以后，就会得到满足要求的橡胶弹性元件参数，实际生产中，就可以按照计算出的各个参数以及实际的用途情况，来制作出合适的橡胶弹性元件。
另外，在实际使用过程中，应该采取有效的措施避免橡胶弹性元件的磨损，因为橡胶弹性元件很容易受损，一旦磨损发生，将会使轨道车辆的安全性急剧降低，而且还会影响其运行的稳定性，所以，在实际使用时，应该注意避免在极限条件下使用，减少使用时间，以避免磨损。
总之，在轨道车辆系统设计过程中，橡胶弹性元件的设计计算是一个非常重要的过程，从而可以得到满足使用要求的橡胶弹性元件，在实际使用过程中，应采取有效的措施来避免它的磨损，以保证轨道车辆的安全性以及轨道车辆的稳定运行。
橡胶弹簧有限元分析方法研究
橡胶弹簧有限元分析方法研究橡胶弹簧是一种广泛应用于汽车、机械、纺织机械、仪器仪表、建筑以及航空航天等领域的一种重要零部件。
由于橡胶弹簧的复杂性及多变性，传统的理论计算容易产生错误和误差，使得应用中出现了大量的设计性不足、质量性不足、生产性不足以及可靠性性不足等缺陷。
为了解决这一问题，有必要研究采用有限元分析方法，以便更好地预测和模拟橡胶弹簧的动态行为。
首先，要正确理解有限元分析的基本原理。
有限元分析是运用数学模型来分析实际现象的数值方法，是一种建立在空间分布的受力状态下的结构分析方法。
有限元分析的基本思想是，将物理结构分解成若干有限的元素，而且每一个元素的力学性质可以求解。
通过定义每一个元素的节点坐标，即可建立出完整的结构模型。
此外，有限元分析还能够确定结构模型在任意荷载条件下的变形大小以及分析模型的强度。
其次，要正确应用有限元分析技术研究橡胶弹簧。
橡胶弹簧是一种特殊的力学结构，困难在于它具有复杂的拉伸行为、多变的挠曲形状以及具有非线性的材料特性。
因此，在实际的分析过程中，要在计算有限元分析结果的基础上加以考虑，以便准确地反映非线性材料特性，达到尽可能准确的分析结果。
此外，橡胶弹簧的计算模型还要加以完善。
原来，由于橡胶弹簧的动态特性复杂，在实际分析中往往采用简化的板梁模型，然而这种简化模型多采用相同的材料性能，由于模型简化过度而导致结构参数计算不准确，从而影响了计算的准确性。
为此，在实际的计算中，要采用更加复杂的三维有限元模型，考虑到橡胶弹簧结构本身的复杂性，以便准确地反映弹簧的动态行为特性。
最后，要采取有效的控制和管理措施，确保分析结果准确、可靠。
首先，在计算过程中，要严格把控模型分析和计算过程，充分考虑橡胶弹簧的特殊性和复杂性，以保证分析结果准确。
此外，要建立一套完善的计算和控制机制，以便及时发现和处理模型分析的错误。
最后，要对结果进行全面综合评估，以便在确定设计参数时能够及时准确地反映实际情况。
基于有限元法对橡胶弹性关节的设计分析
把芯 轴 （ 心 轴 ） 大 ， 与 外 套 挤 缩 相 比效 果 差 些 。 空 扩 但
挤缩 加工 可 以显著 提 高橡 胶 弹 性关 节 的疲 劳 强 度 ， 与 此 同时 ， 各 向刚度 性能也 将 因此而 发生 变化 。 其
如果 系统 对 橡 胶 弹 性 关 节 的 刚 度 性 能 要 求 不 严 格 ， １ 类型 的橡 胶 弹性 关 节 还 可采 用 外 套 分瓣 式 第 种 结构 ， 也能 消除硫 化 后橡 胶 与 金 属 粘结 面 处 的残余 应 力 。因为 分瓣 的外套 能 够 随橡 胶 一 起 自 由收缩 ， 会 不
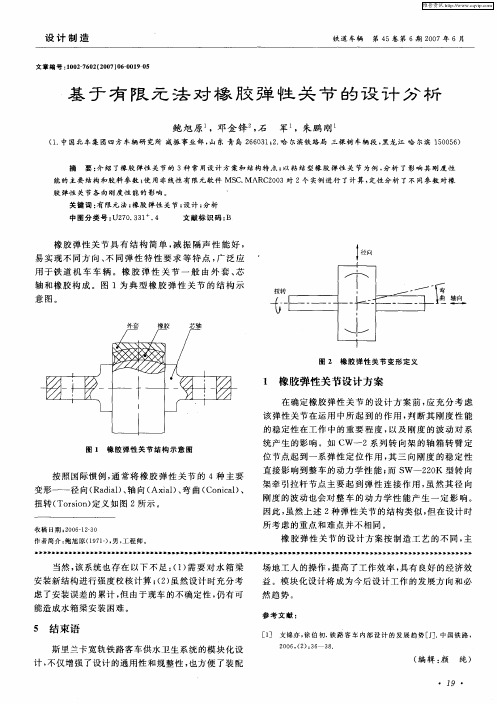
轴 和橡 胶 构 成 。图 １为 典 型 橡 胶 弹 性 关 节 的结 构 示
意图。
外套 橡胶 芯轴
扭转
一
，
／
＿［ 一 －一
一
ｌ塑 曲 甸 ＿ ．
Ｕ
＼～ ／
图 ２ 橡 胶 弹 性 关 节 变 形 定 义
１ 橡胶弹性关节设计方案
在确 定橡 胶 弹性 关 节 的设 计 方 案 前 ， 充 分考 虑 应
中 图分 类 号 ： ７ ． ３ ． Ｕ２ ０ ３ １ ４ 文献标识码 ： Ｂ
橡胶 弹 性关 节 具 有 结 构 简单 ， 振 隔声 性 能好 ， 减
易实 现不 同方 向 、 同 弹 性 特 性 要 求 等 特 点 ， 泛 应 不 广
ｌ 径 向
厂 、
／
用 由外 套 、 芯
收稿 日期 ：０ ６１ －Ｏ ２０ —２３ 作 者 简 介 ： 旭 原 （ ９ 卜） 男 ， 程 师 。 鲍 １７ ， 工
橡 胶 弹性 关 节的设 计 方 案按 制 造工 艺 的 不 同 ， 主
场 地工 人 的操作 ， 高 了工 作效 率 ， 有 良好 的经济效 提 具 益 。模块 化设 计将 成 为今后 设计 工作 的发展 方 向和必
橡胶工业中有限元计算问题过盈配合
橡胶工业中有限元计算问题过盈配合作者：清华大学工程力学系范成业摘要本文分析了过盈配合的有限元计算时用到超弹性本构时可压缩性对计算结果的影响情况，得到在过盈配合中必须考虑这种可压缩性的结论并分析考虑可压缩性的原因。
1、引言过盈配合是橡胶工业中的一种常见的配合方式。
橡胶为超弹性材料，有限元计算中通常假定为不可压或者几乎不可压。
本文首先给出一种不可压橡胶模型过盈配合的理论解，并与ABAQUS计算解进行比较。
进一步本文探讨过盈配合中假定橡胶不可压时遇到的问题，提出处理过盈配合中橡胶计算的方法。
2、可压模型理论解与ABAQUS数值解的比较2.1、理论解理论解模型如图1，内层为钢，中间不可压橡胶，最外层为钢给出橡胶和橡胶之间的过盈量求整个结构的应力应变状态假设平面应变状态。
图1 理论解模型示意图本构方程：对于钢：对于橡胶：2.1材料性质：钢：E=210000v=0.3橡胶：C10=0.461312, C20=0.01752, C30=8.8e-05，其余为0，（三次多项式模型，材料不可压缩）2.2.2几何特性如图2所示，R59.50为内层钢的半径和中间层橡胶的内径，R73.00为中间层橡胶的外径，R71.10为外层钢的内径，R80.00为外层钢的外径。
图2 不可压模型算例几何特征理论解与计算解的比较（理论解由Maple计算得出）表1 理论解与ABAQUS 解的比较半径（mm ） 理论解 ABAQUS 计算解 误差 位移59.5 -9.2984E-02 -9.73152E-2 4.6% 径向应力S1159.5（钢）-660.51 -631.60 -4.38% 59.5（橡胶） -660.51 -631.60 -4.38% 73.0（橡胶） -660.51 -631.60 -4.38% 71.1（钢） -660.51 -664.30 0.57% 80.0（钢） 0 28.15 － 环向应力S2259.5（钢）-660.51 -631.20 -4.44% 59.5（橡胶） -660.51 -631.20 -4.38% 73.0（橡胶） -660.51 -631.40 -4.38% 71.1（钢） 5626.36 5541.00 -1.52% 80.0（钢）4956.854957.000.00%3、可压缩模型橡胶的应变能采用多项式模型时，在静水压力荷载下p 与J 的关系如下：用ABAQUS 对这1-4组系数进行评估：图3 不同系数对应的橡胶静水压力下的应力应变关系将这六种橡胶本构代入第二部分中的算例中进行计算结果如下：图4 第6组系数对应的位移图图5 第1组系数对应的位移图由图4和图5容易看到这两组系数对应的位移差异非常大。
采用ANSYS的橡胶弹簧的有限元建模与仿真
采用ANS Y S的橡胶弹簧的有限元建模与仿真任茂文1,周长峰2(1江苏电大泗洪分校,泗洪223900;2东南大学机械工程学院,南京210096)摘要:建立AD250铰接式自卸车前悬架橡胶弹簧的参数化非线性有限元接触模型,比较橡胶弹簧实体建模与平面建模的计算精度,并分析大载荷下橡胶弹簧内部应力的分布,得到的结果与试验结果有很好的一致性。
此模型可为橡胶弹簧结构的参数优化提供理论支持。
关键词:橡胶弹簧;非线性;有限元分析中图分类号:U463133+415 文献标识码:B 文章编号:1671—3133(2008)05—0059—04Rubber spr i n gπs f i n ite elem en t si m ul a ti on m odeli n gand si m ul a ti on ba sed on ANS Y SRen Mao2wen1,Zhou Chang2feng2(1School of Sihong,J iangsu T V University,Sihong223900,J iangsu,CHN;2School ofMechanicalEngineering,Southeast University,Nanjing210096,CHN)Abstract:The AD250hinge type du mp truck fr ont sus pensi on rubber s p ringπs para metrizati on non2linear finite ele ment contact model has been established.The computati onal accuracies of the rubber s p ring entity modelling and the p lain modelling have been compared.Besides,the rubber s p ring internal stress distributi on under the big l oad has been analyzed.There are good unif or m ity bet w een the result and the experi m ental result.This model may p r ovide the theoretical support for the para meter op ti m izati on of the rubber s p ring structure.Key words:Rubber s p ring;Non2linear;Finite ele ment analysis 近年来,具有可变刚度特点的橡胶弹簧和空气弹簧在工程车辆的悬架系统中已逐渐得到应用。
橡胶工业中的有限元计算问题
中文摘要摘要作为一种工程材料硫化橡胶早在19世纪就被广泛的应用。
由于它良好弹性的特性被用于承载结构轴承，密封圈，吸收震动的衬垫，连接器，轮胎等。
然而，不同于金属材料仅需要几个参数描述其材料特性，橡胶的行为复杂，材料本构关系是非线性的。
它的力学行为对温度，环境，应变历史，加载的速率都非常敏感，这样使得描述橡胶的行为变得更为复杂。
橡胶的制造工艺和成分也对橡胶力学性能有显著的影响。
这也意味着橡胶作为工程材料的研究是一段不断的尝试和改进的过程，而不是完全彻底的理解。
幸运的是，由于计算机以及有限元分析的飞速发展，我们可以借助计算机来对超弹性材料工程应用进行深入研究以及优化设计。
本文给出如何用有限元方法来分析工业中的橡胶元件的力学性能的完整的方法，包括选取橡胶的本构模型，拟合本构模型，有限元建模，处理计算结果。
有限元分析的精度是直接与输入的材料数据相关的。
理想情况下，数据应该来自一系列的独立的实验。
本文给出了常用的用于拟合橡胶本构关系的实验方案。
另外本文详细讨论了一种橡胶元件中常用的超弹性材料轴对称过盈配合问题。
分别用解析的方法和有限元计算方法详细研究了此问题，包括平面应变大变形和小变形的解析解，有限元解，平面应力的小变形理论解，平面应力情况大变形和小变形的有限元解，橡胶体积模量对过盈配合的影响，接触面的摩擦系数对过盈配合的影响。
关键词：橡胶过盈配合超弹性大变形- I -目录摘要 (II)Abstract（英文摘要） (III)目录 (V)第一章超弹性材料本构关系 (1)引言： (1)1.1 超弹性模型概况 (1)1.2 橡胶模型的特征 (3)1.3 常用的橡胶本构模型介绍 (3)1.3.1 多项式形式及其特殊情况 (3)1.3.1.1 Mooney-Rivlin模型和Neo-Hookean模型 (4)1.3.1.2 Yeoh形式（Yeoh, 1993） (5)1.3.2 Ogden形式 (6)1.3.3 Arruda-Boyce形式 (6)1.3.4 Van der Waals模型 (7)1.4 本文的主要内容 (8)第二章超弹性材料过盈配合的解析解和数值解 (10)引言： (10)2.1 橡胶大变形和小变形本构关系 (11)2.1.1 大变形 (11)2.1.2 小变形 (12)2.2 平面应变情况下的解析解和有限元解 (14)2.2.1解析解 (14)2.2.1.1 线弹性小变形解析解 (14)2.2.1.2 大变形超弹性本构关系解析解 (15)2.2.1.3 线弹性与超弹性解析解的比较 (17)- II -2.2.2解析解与ABAQUS数值解的比较 (20)2.3 平面应力情况下解析解和有限元解 (22)2.3.1 解析解（小变形线弹性） (22)2.3.2有限元解 (23)2.3.2.1解析解与有限元解（线弹性橡胶本构关系）的比较 (23)2.3.2.2 两种本构关系的有限元解的比较（线弹性和超弹性） (25)2.4 可压缩性对过盈配合的影响 (26)2.5 摩擦系数对过盈配合的影响 (27)2.5.1 ABAQUS中接触的定义 (28)2.5.2 ABAQUS模拟过盈配合 (28)2.6 本章总结 (32)第三章实验拟和超弹性本构模型系数 (33)引言： (33)3.1 超弹性材料试验简介 (33)3.1.1 多种应变状态测试 (34)3.2 超弹性材料基本试验 (35)3.2.1单轴拉伸实验 (35)3.2.2 纯剪（平面拉伸）实验 (36)3.2.3等轴拉伸实验 (37)3.2.4压缩实验 (38)3.2.5体积压缩实验 (39)3.3 弹性本构模型中的系数 (39)3.3.1 最小二乘法用于多项式形式 (40)3.3.2 非线性最小二乘法 (40)3.3.3 非线性最小二乘法用于Ogden模型 (41)第四章橡胶定位器的有限元计算 (43)4.1 定位器建模 (43)4.1.1数值方法的选择 (44)4.1.2 有限元建模 (44)- III-4.2 静力学分析 (45)4.2.1 垂向刚度 (45)4.2.2 横纵向刚度 (46)4.2.3 静态分析结果对比 (48)4.3 动态分析 (49)4.3.1 模态分析基本方程 (49)4.3.2 定位器振型有限元分析结果 (49)4.4 本章总结 (52)第五章球铰的有限元计算 (53)5.1 球铰建模 (53)5.1.1数值方法的选择 (54)5.2 静力学分析 (54)5.2.1有限元计算扭转刚度 (55)5.2.2 偏转刚度 (56)5.2.3 有限元计算与实验的比较 (58)5.3 本章总结 (59)第六章结论 (60)参考文献 (61)致谢 (62)附录A 纯剪实验方法 (63)附录B 体积模量实验方法 (65)个人简历和在学期间的研究成果及发表的学术论文 (67)- IV -目录第一章超弹性材料本构关系引言作为一种工程材料硫化橡胶早在19世纪就被广泛的应用。
有限元法在机车车辆橡胶元件设计中的应用
③ 应 力和应 变之 间存 在一一 对应关 系 ；
④存在一个应变能函数， 应力可以从应变能函数
求得 。
具有特性④ 的材料 成为超弹性材料 ， 橡胶是一种主 要 的超 弹性材料 ： 橡 胶 的本 构理 论最重 要的是 确定应 变能函数 ， 可通过一些 方法来实现 。 此处 不详细说 明。
的 阻尼 作用 依赖 于 其滞 后 现象 。正是 由于 滞后 现象 ， 橡胶 的拉 伸一 回缩循 环变化均需 克服链段 间的 内摩擦 阻 力而 产 生 内耗 。 橡 胶在 很窄 的玻璃 态转 变 区域 内 ，
机 车车 辆 的动力学 要求 。在机 车车辆 正 常运行 时 ， 冲
击载荷 相对较 小 ， 相 应产生 恒 定刚度 实现 平稳 行驶 ；
４ ０
Ｏ
０
４ ０
８ ０
１ ２ ０
差异 也有利 于缓 和 冲击 ；橡胶 弹性元 件在 低频段 时 ， 可 以看成 是一个 由刚度 和阻尼 组成 的集 中参数元 件 ，
位移 ／ ａｍ ｒ
主要 由橡胶 减振 ；工作在 高频率 时候 ， 弹性元 件 中金
属 件的 刚度 将起 主要 作用 。
当机车 车辆 遭遇 意外情 况 ， 产 生强 大 冲击载荷 时 ， 橡
胶元件 能迅 速产生大 的阻抗 力 ， 防止 因位移 过大造成
机车 车辆异 常运行 而发 生事故 。
其模 量 大幅度 下 降 ， 具有 足够 高 的损 耗 囚子 ， 在一 定
１ ６ ０
的振 动频率 范 围内分子 基团之 间能够 相互耦 合 ， 并 在
向刚度要求可 以改善车辆乘 坐舒适性并 能提高车辆 运 行速度 。 而一般金属零件很难满 足 ， 橡胶 儿件可以通过
橡胶弹簧有限元分析方法研究
橡胶弹簧有限元分析方法研究
本文主要介绍了橡胶弹簧有限元分析方法的研究。
橡胶弹簧是机械系统中常用的一种传动元件，其特性对机械系统性能有着重要影响。
有限元分析是一种可以用于估计、预测、设计和优化机械系统结构性能的有效工具。
本文以橡胶弹簧为研究对象，采用ANSYS软件计算分析，研究了橡胶材料的力学特性及振动和挠性对橡胶弹簧的影响，以期达到更准确地预测橡胶弹簧的运动及力学性能的目的。
首先，本文介绍了橡胶材料的基本特性及其应力-应变特性，并
分析了橡胶材料在不同温度条件下的变形性能，以此为基础，使用ANSYS软件对橡胶弹簧进行了有限元分析，分析了橡胶弹簧的振动性能。
结果表明，随着温度的升高，橡胶弹簧的振动衰减率下降，振动分量逐渐减少，显示出橡胶材料特有的温度相关性能。
此外，本文还就橡胶弹簧的挠度进行了分析，从而评估他们在不同载荷条件下的力学特性。
研究发现，橡胶弹簧的挠度随荷重的增大而增大，其弹性模量呈现先减小后增大的趋势，说明橡胶弹簧能够很好地适应不同的荷载环境。
最后，本文介绍了基于有限元分析的橡胶弹簧设计优化方法，并结合实际工程分析，建立了一种基于受力的设计优化模型。
与实验结果比较，室温下橡胶弹簧的模量和频率均有较好的精度，表明基于有限元的设计优化方法是有效的。
综上所述，本文针对橡胶弹簧的有限元分析方法进行了研究，并介绍了基于有限元分析的设计优化方法。
有限元分析不仅可以更准确
地预测橡胶弹簧的运动和力学特性，而且可以有效地对它们进行设计优化。
因此，本文研究对于提高橡胶弹簧设计水平具有重要意义。
橡胶弹性元件有限元分析技术应用现状的探讨
橡胶弹性元件有限元分析技术应用现状的探讨黄友剑、卜继玲、程海涛、刘建勋中国南车株洲时代新材料科技股份有限公司，株洲，412007摘要：本文较为全面地阐述了时代新材在有限元使用方面的总体状态和技术上所呈现出来的技术成果。
特别就设计人员中的有限元仿真的总体概况、橡胶弹性元件所涉及到的仿真分析软件的应用、仿真分析技术在典型产品开发中的成功应用三个方面进行了重点论述。
关键词：橡胶弹性元件、ABAQUS、仿真分析1、橡胶弹性元件结构仿真分析技术的总体概况1.1设计人员对有限元技术的使用上升到较为合理的水平基于上述有限元仿真分析的重要性，有限元仿真分析在时代新材弹性元件的设计人员中得到较为全面的普及。
经过多年来的努力，现在设计人员的有限元仿真分析能力的程度达到较高的水平。
专业从事有限元仿真分析的设计人员占到15%，基本会使用有限元仿真分析的设计人员达到60%，不会使用有限元仿真分析的设计人员仅占25%，有限元分析技术在弹性元件研发部已经开花结果，大力促进了本部弹性元件产品的研发。
图1-1 设计人员使用仿真分析的人员构成1.2有限元技术在开发项目中的参与程度达到了较为合理的高度有限元仿真分析在项目开发中的作用至关重要，可以参与整个项目的开发流程。
在产品的开发过程中，前期对产品进行性能仿真分析，缩短设计和分析周期；后期模拟各种试验方案，减小试验时间和费用。
时代新材弹性元件承担的开发项目中，有限元仿真分析的参与程度很高，经调查显示：开发的项目中全部应用有限元仿真分析完成的项目数量达到25%，部分应用有限元仿真分析的项目数量达到55%，完全没有应用有限元仿真分析的项目数量仅占20%，日常的产品研发表明，有限元分析技术已经大幅度渗透在弹性元件研发部的产品研发中，已经成为产品研发密不可分的一个重要手段。
图1-2 有限元技术在开发项目中的参与程度统计1.3有限元仿真分析技术大力提升产品的研发设计能力时代新材弹性元件设计人员的仿真分析能力，经过多年来经验的积累，得到很大幅度的提升，分析的精确度和准确度达到一定的水平。
橡胶弹簧有限元分析方法研究
橡胶弹簧有限元分析方法研究橡胶弹簧是一种由橡胶弹性体制成的传统型弹簧，广泛应用于补偿系统、模拟系统、消声系统、减振系统等机械系统中，是一种技术性和经济性相结合的轴承元件，其中的弹性变形能起着重要作用。
有限元分析是一种现代的计算机分析技术，可以模拟物理系统中复杂问题。
有限元分析可以有效地解决橡胶弹簧的力学性能，但是，橡胶弹簧的尺寸是多变的，而有限元分析需考虑到橡胶弹簧因材料和尺寸变化而引起的应力应变不确定性，这是有限元分析技术面临的挑战。
因此，有必要对橡胶弹簧的力学行为进行有限元分析以确定材料性能和尺寸影响，研究不同的材料参数以及不同的尺寸参数对橡胶弹簧性能的影响，以期获得良好的性能和可靠性，为现代机械系统的设计提供有效的参数分析。
首先，有限元分析需要建立一个有效的数学模型，以描述橡胶弹簧的力学特性。
建模时，需要充分考虑在不同尺寸变化以及不同的材料参数下的影响，如橡胶的硬度、松紧度等，以及在承载荷重下的应力应变变化。
考虑到橡胶弹簧的非线性特性，需要将橡胶弹簧的应力应变关系式描述为一个非线性模型，以准确反映橡胶弹簧的弹性变形能力。
其次，有限元分析需要建立一个有效的方程组，以涵盖不同材料参数和尺寸参数的影响，以及材料与环境变化。
在模型建立之前，需要确定有限元分析所需的各参数，包括材料参数、尺寸参数、环境变量、荷载及其变化等。
建立有限元分析方程组后，再进行数值求解，以得到详细的有限元结果，并分析橡胶弹簧的力学行为，如应力应变关系、延伸率等。
最后，基于有限元分析结果，进行有关参数的分析，如材料参数、尺寸参数及其变化的影响等，以及环境变化的影响等。
通过模拟分析，结合弹簧实际应用情况，得出最佳的设计参数。
通过以上研究，可以有效地了解橡胶弹簧的力学行为，并为现代机械系统的设计和应用提供全面的参考依据。
未来，有限元技术将成为研究橡胶弹簧的关键技术，为实际应用提供有效的参考参数。
综上所述，通过建立一个有效的数学模型、建立一个有效的方程组和对参数进行分析，可以有效地利用有限元分析方法研究橡胶弹簧的力学行为，以期取得良好的性能和可靠性，为现代机械系统的设计提供有效的参数分析参考。
橡胶受热膨胀 有限元
橡胶受热膨胀有限元
有限元分析（Finite Element Analysis，FEA）是一种用于模拟和分析结构在受力或受热等条件下的行为的工程工具。
如果你想研究橡胶在受热膨胀过程中的行为，可以通过有限元分析来模拟和分析。
以下是一般步骤：
建立模型：使用有限元软件，首先建立橡胶结构的三维模型。
这可能包括定义橡胶的几何形状、材料属性和约束条件。
定义材料属性：在模型中定义橡胶的热膨胀系数和其他与热膨胀相关的材料属性。
施加热负载：模拟热膨胀过程，通过在模型中施加热负载来模拟橡胶在受热时的行为。
这可以通过定义温度场或直接施加温度载荷来实现。
设置分析类型：根据研究的问题，选择适当的有限元分析类型。
对于热膨胀，通常使用热-结构分析。
网格划分：在模型中应用网格划分，确保在橡胶结构中足够细致的网格，以获得准确的结果。
求解模型：运行有限元分析，求解模型的行为。
软件将提供关于橡胶结构在受热膨胀时的位移、应力和温度等信息。
结果分析：分析有限元分析的结果，关注橡胶的形变、应力分布、温度变化等信息。
这有助于理解橡胶在受热膨胀过程中的行为。
优化设计：根据分析结果进行设计优化，例如调整材料属性、结构形状或其他参数，以满足特定的性能需求。
请注意，有限元分析是一种高级的工程工具，需要具备一定的工程知识和经验。
在进行有限元分析之前，建议咨询专业工程师或有限元分析专家的建议。
橡胶弹簧有限元分析方法研究
橡胶弹簧有限元分析方法研究
随着科学技术的进步，橡胶弹簧已经成为工业应用领域里不可或缺的一种元件了。
由于它具有优良的弹性和耐磨性，能够满足大多数应用要求，因此被广泛地用于汽车、家电、机械制造等行业。
然而，它们的动态性能是非常复杂和不确定的，需要精准的分析方法来确定它们的最佳组合及应用。
因此，有限元分析工具已经成为橡胶弹簧研究的重要工具。
有限元法可以将复杂的几何形式和弹性本构关系简化为一组数学问题，帮助设计者准确地预测弹簧的行为。
它还可以计算出弹簧的应力应变特性，以便设计者能够准确地识别出弹簧的关键参数。
基于有限元分析的研究，已经建立起了一个完整的橡胶弹簧模型，该模型可以用于研究不同形状和组件的弹簧以及对物理现象的响应。
该模型可用于优化设计，以提高橡胶弹簧的功能性能，减少生产成本。
此外，有限元分析还可以与其他研究方法结合起来，来模拟弹簧结构的复杂动态行为。
该方法也能够更加准确地模拟和分析不同材料的弹簧的变形情况，以及弹簧表面摩擦对其特性的影响。
总之，有限元分析已经成为弹簧设计和分析领域里不可或缺的重要工具。
它非常有助于设计者计算弹簧结构的应力应变特性，优化设计以满足最佳功能性能，以及模拟不同材料和应用的复杂动态行为。
未来的研究将不断探索有限元分析在橡胶弹簧研究中的更广泛应用，以提高其功能性能和精确性。
- 1 -。
ABAQUS在橡胶制品领域的研究与应用
ABAQUS在橡胶制品领域的探究与应用橡胶制品作为一类常见的材料，广泛应用于汽车、航空航天、建筑等行业。
随着科学技术的不息进步，传统的试验探究逐渐无法满足对橡胶制品的性能需求。
ABAQUS作为一种有限元分析软件，可以对橡胶材料进行力学性能分析，为橡胶制品的探究与应用提供了一种新的方法。
主要包括以下几个方面。
起首是弹性力学性能分析。
ABAQUS可以模拟橡胶材料在受力时的弹性行为。
通过建立适当的材料模型和边界条件，可以计算出橡胶制品在受力时的变形、应力和应变分布。
在汽车轮胎的设计中，通过ABAQUS可以猜测轮胎在不同路面条件下的变形状况，为改善轮胎的抓地力和舒适性提供科学依据。
其次是断裂力学性能分析。
橡胶制品在使用过程中可能经受各种复杂的外力作用，容易出现断裂现象。
通过ABAQUS的有限元分析方法，可以猜测橡胶制品在不同外力条件下的断裂位置和形态。
这可以为橡胶制品的设计和材料选择提供指导，提高产品的可靠性和使用寿命。
此外，ABAQUS还可用于探究橡胶材料的疲惫性能。
由于橡胶制品可能长时间受到往来循环载荷的影响，容易发生疲惫毁伤。
通过ABAQUS可以模拟橡胶材料在疲惫载荷下的变形和应力分布，从而猜测其疲惫寿命。
这对于橡胶制品的设计和使用寿命评估具有重要意义。
除了力学性能的分析外，ABAQUS还可以结合材料模型和温度、湿度等外界因素进行热学性能分析。
橡胶材料在不同温度和湿度环境下的物理性能会发生变化，这些因素对橡胶制品的使用性能也有很大影响。
通过ABAQUS的有限元分析，可以模拟橡胶材料在复杂热湿环境下的变形和性能变化。
这为橡胶制品的设计和使用提供了科学依据。
需要注意的是，不仅仅局限于上述几个方面。
随着科学技术的进步，ABAQUS在材料建模、失效分析、性能优化等方面的应用也逐渐得到推广。
橡胶制品是一个复杂的体系，涉及材料科学、力学和热学等多个学科领域。
将ABAQUS与其他学科的探究方法相结合，可以更全面地探究橡胶制品的性能与应用。
橡胶弹簧有限元分析方法研究
橡胶弹簧有限元分析方法研究摘要：本文旨在探讨橡胶弹簧有限元分析方法的特点、优势和应用。
首先，本文阐述基本有限元理论，并运用有限元方法对橡胶弹簧的物理性能进行分析。
其次，文章将针对橡胶弹簧的弹性、摩擦、塑性、抗疲劳等物理性能进行分析，并给出相应的分析方法。
最后，本文还综述了有限元方法在橡胶弹簧分析过程中的重要应用意义。
关键词：橡胶弹簧；有限元分析；弹性；摩擦；塑性；抗疲劳中文文章：橡胶弹簧有限元分析方法研究摘要本文旨在探讨橡胶弹簧有限元分析方法的特点、优势和应用。
首先，本文阐述基本有限元理论，并运用有限元方法对橡胶弹簧的物理性能进行分析。
其次，文章将针对橡胶弹簧的弹性、摩擦、塑性、抗疲劳等物理性能进行分析，并给出相应的分析方法。
最后，本文还综述了有限元方法在橡胶弹簧分析过程中的重要应用意义。
一、本有限元理论介绍有限元分析是一种求解在计算机环境中复杂工程结构问题的计算方法。
其基本概念是将复杂的结构分解成有限个基本的、相对简单的元素，并利用适当的数学工具和计算机进行分析。
二、橡胶弹簧有限元分析方法研究（1）分析橡胶弹簧的弹性特性橡胶弹簧的弹性和弹性系数是该弹簧的主要特性之一，从而影响该弹簧的性能。
在使用有限元分析方法分析橡胶弹簧的弹性特性时，应完善弹簧的有限元模型，确定细节的物理参数，模拟合理的弹簧材料。
然后，利用有限元方法对橡胶弹簧进行分析，以确定其弹性特性的变化。
（2）分析橡胶弹簧的摩擦特性橡胶弹簧的摩擦特性与其弹性特性有关，和环境温度相关性强。
使用有限元分析方法来分析橡胶弹簧的摩擦特性，首先应完善有限元模型，然后以恒温方式进行模拟分析，在给定温度范围内，根据载荷和变形获得摩擦系数。
（3）分析橡胶弹簧的塑性特性橡胶弹簧的塑性特性在工程中可能会受到较大的变形，这将影响其实际应用。
使用有限元分析方法来分析橡胶弹簧的塑性特性时，首先应完善有限元模型，然后以恒载荷和恒变形方式进行模拟分析，根据载荷和变形获得塑性模量。
基于有限元方法的橡胶弹性件设计开发流程
基于有限元方法的橡胶弹性件设计开发流程史文库、陈志勇、姜莞 吉林大学汽车工程学院一、应用有限元方法进行橡胶减振隔振件设计的必要性和意义橡胶包括天然橡胶及合成橡胶，是无定形的高聚物[1]。
橡胶是一种超弹性材 料，具有良好的伸缩性和复原性。
橡胶的弹性与金属的弹性不同，若将金属棒和 橡胶棒各用力拉伸，橡胶的最大伸长通常在 500~1000%之间，处在小变形区域 外，没有固定的杨氏模量，小变形范围内的杨氏模量约为 1.0MPa，而弹性变形 仅为 1%或更小[2]。
对于橡胶材料来说，对一般工程材料适用的小变形理论已经 不再适用，即当载荷比较大时，应力应变不再保持为线性关系，但不会产生永久 变形，当载荷一旦消失，变形将完全恢复。
并且橡胶元件的形状对其弹性特性有 复杂的影响，因此，不能用传统的理论进行设计和计算[3]。
如果单纯靠试验的方 法设计，其成本较高。
随着计算机技术的发展以及有限元理论的完善，用有限元 方法对橡胶隔振件设计计算成为了较好的方法。
有限元方法的优势在于设计周期 短，成本低，精度高，能够对橡胶隔振件进行非线性计算。
二、目前的国内外橡胶件设计开发现状分析早在 20 世纪 70 年代，橡胶制品的有限元分析已经成为橡胶制品设计者的主 要设计手段，一些商业化的非线性有限元软件MARC、ABAQUS、ADINA等被 用来对橡胶制品进行辅助分析[4]。
世界上一些著名的科研机构和生产橡胶制品的 公司开始对橡胶制品进行有限元分析，以提高橡胶制品的质量。
其中包括英国的 MERL公司，欧洲的RAPRA公司，美国的PSP公司，HLA Engineers公司，英国 TUN ABDUL RAZAK研究中心的橡胶材料咨询中心， Akron橡胶研发实验室等以 及世界上一些著名的轮胎公司都在橡胶制品的有限元分析方面有非常成熟的研 究。
有限元分析技术已经广泛应用到生产中，并且在产品研制中发挥着重要作用 [5] 。
我国橡胶制品的有限元分析起步较晚， 但随着国外大型有限元软件引入我国， 国内的一些高校和科研机构已经开始对橡胶制品进行有限元分析。
橡胶接触的有限元分析
圆球与橡胶垫接触的有限元分析一、问题描述分别模拟钢球以及橡胶球在以=0.95F N 的垂向载荷挤压硅橡胶（PDMS ）垫时的变形情况。
钢球直径1=12.7mm Φ，硅橡胶圆盘直径2=50mm Φ，厚度d=5mm .已知硅橡胶杨氏模量 1.0363E MPa =，泊松比0.499σ=，为超弹性材料。
分别模拟小球为刚性材料和为橡胶材料时两种情况下硅橡胶垫的变形情况。
二、有限元分析由于橡胶本构关系的非线性化，以及橡胶制品在应用时的大变形、接触非线性边界条件使其工程模拟变的非常困难。
模拟的准确性与采用的本构关系模型以及模型中材料常数测试的准确性有密切关系。
本次分析以橡胶中常用的Mooney-Rivlin 材料作为橡胶的本构模型。
1、 材料参数的确定Mooney-Rivlin 模型的基本理论不赘述，通过查阅相关文献得知Mooney-Rivlin 模型中材料常数与材料弹性模量有如下关系：10016()E C C =+并且有经验公式：01100.25C C =可以计算Mooney-Rivlin 模型中材料常数1001138173,34543C C ==，用于有限元分析中定义材料。
2、 钢球与硅橡胶盘接触由于钢球与硅橡胶接触时钢球变形可以忽略，可以把钢球看做刚体（Rigid body ），建有限元模型如下：图1 刚性球接触时的有限元模型分析结果如下：图2 刚性球接触时圆盘变形云图最大变形为图中红色部分，为42.82100.282y m mm-∆=⨯=3、橡胶球与硅橡胶圆盘接触将球划分网格，并定义为可变性体（Deformable body）有限元模型如下：图3 橡胶球与硅橡胶圆盘接触时的有限元模型将球看做可变性体，与圆盘赋相同的材料进行分析，圆盘变形云图如下：图4 橡胶球接触时圆盘变形云图最大变形为图中红色部分，为41.62100.162z m mm -∆=⨯=。
弹性胶泥缓冲器关键件的有限元分析毕业设计任务书
大学毕业设计任务书学院、系：专业：机械设计制造及其自动化学生姓名：学号：设计题目：弹性胶泥缓冲器关键件的有限元分析起迄日期:指导教师:系主任:发任务书日期: 年月日任务书填写要求1．毕业设计任务书由指导教师根据各课题的具体情况填写，经学生所在系的负责人审查、签字后生效。
此任务书应在毕业设计开始前一周内填好并发给学生；2．任务书内容必须用黑笔工整书写或按教务处统一设计的电子文档标准格式（可从教务处网页上下载）打印，不得随便涂改或潦草书写，禁止打印在其它纸上后剪贴；3．任务书内填写的内容，必须和学生毕业设计完成的情况相一致，若有变更，应当经过所在专业及系主管领导审批后方可重新填写；4．任务书内有关“学院、系”、“专业”等名称的填写，应写中文全称，不能写数字代码。
学生的“学号”要写全号（如020*******），不能只写最后2位或1位数字；5．有关年月日等日期的填写，应当按照国标GB/T 7408—94《数据元和交换格式、信息交换、日期和时间表示法》规定的要求，一律用阿拉伯数字书写。
如“2004年3月15日”或“2004-03-15”。
毕业设计任务书1．毕业设计的任务和要求：在AMSYS软件平台上，对某型号弹性胶泥缓冲器结构进行有限元建模，并对结构进行应力应变分析，分析结构的薄弱环节，对结构设计进行验证校核。
2．毕业设计的具体工作内容：1 学习有限元分析软件ANSYS的相应功能.2 分析缓冲器的工作机理，在ANSYS上建立缓冲器结构的有限元模型。
3 对建立的有限元模型进行应力应变计算，4 根据计算结果对结构设计进行分析。
5 翻译外文文献一篇。
毕业设计任务书3．对毕业设计成果的要求：1 毕业设计论文一篇2 设计过程中产生的有限元模型数据文件。
注：包括毕业设计、图纸、实物样品等。
4．毕业设计工作进度计划：起迄日期工作内容年2月 21日~3 月12 日3月 13 日~4月10 日 4月11日~5月15 日5月16日~ 6月 10日查阅文献，完成开题报告学习有限元分析软件ANSYS的相应功能分析缓冲器的工作机理，在ANSYS上建立缓冲器结构的有限元模型。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基于有限元方法的橡胶弹性件设计开发流程
史文库、陈志勇、姜莞 吉林大学汽车工程学院
一、应用有限元方法进行橡胶减振隔振件设计的必要性和意义
橡胶包括天然橡胶及合成橡胶，是无定形的高聚物[1]。
橡胶是一种超弹性材 料，具有良好的伸缩性和复原性。
橡胶的弹性与金属的弹性不同，若将金属棒和 橡胶棒各用力拉伸，橡胶的最大伸长通常在 500~1000%之间，处在小变形区域 外，没有固定的杨氏模量，小变形范围内的杨氏模量约为 1.0MPa，而弹性变形 仅为 1%或更小[2]。
对于橡胶材料来说，对一般工程材料适用的小变形理论已经 不再适用，即当载荷比较大时，应力应变不再保持为线性关系，但不会产生永久 变形，当载荷一旦消失，变形将完全恢复。
并且橡胶元件的形状对其弹性特性有 复杂的影响，因此，不能用传统的理论进行设计和计算[3]。
如果单纯靠试验的方 法设计，其成本较高。
随着计算机技术的发展以及有限元理论的完善，用有限元 方法对橡胶隔振件设计计算成为了较好的方法。
有限元方法的优势在于设计周期 短，成本低，精度高，能够对橡胶隔振件进行非线性计算。
二、目前的国内外橡胶件设计开发现状分析
早在 20 世纪 70 年代，橡胶制品的有限元分析已经成为橡胶制品设计者的主 要设计手段，一些商业化的非线性有限元软件MARC、ABAQUS、ADINA等被 用来对橡胶制品进行辅助分析[4]。
世界上一些著名的科研机构和生产橡胶制品的 公司开始对橡胶制品进行有限元分析，以提高橡胶制品的质量。
其中包括英国的 MERL公司，欧洲的RAPRA公司，美国的PSP公司，HLA Engineers公司，英国 TUN ABDUL RAZAK研究中心的橡胶材料咨询中心， Akron橡胶研发实验室等以 及世界上一些著名的轮胎公司都在橡胶制品的有限元分析方面有非常成熟的研 究。
有限元分析技术已经广泛应用到生产中，并且在产品研制中发挥着重要作用 [5] 。
我国橡胶制品的有限元分析起步较晚， 但随着国外大型有限元软件引入我国， 国内的一些高校和科研机构已经开始对橡胶制品进行有限元分析。
清华大学的吕 振华教授、华南理工大学的上官文斌教授、吉林大学的史文库教授等在橡胶弹性 件的有限元分析和设计方面都承担了国内重大项目， 并且有较为成熟的技术和设 计经验。
三、对橡胶件进行有限元分析的流程
1）确定橡胶材料的本构关系模型。
橡胶材料不同于金属材料仅需要几个参数 描述其材料特性，橡胶的行为复杂，材料本构关系是非线性的。
它的力学行为对 温度，环境，应变历史，加载的速率都非常敏感，这样使得描述橡胶的行为变得 更为复杂。
对于各向同性的体积不可压缩或体积近似不可压缩的橡胶材料，其非 线性弹性特性用超弹性模型描述。
人们为了表征橡胶材料的超弹性本构模型已经 做了大量的工作，这些工作可以归纳为两大类：一类是根据统计热力学而进行的
尝试；另一类则是把橡胶材料作为一个连续介质的唯象理论。
几种常见的本构关 系模型包括：多项式模型、Mooney-Rivlin模型、减缩多项式模型、Neo-Hookean 模型、Yeoh模型、Ogden模型、Van der Waals模型等[6]。
为了确定橡胶材料的本 构模型中的未知参数， 需要对橡胶材料进行材料试验， 所需的试验包括单轴拉压、 等双轴拉压、平面剪切和体积试验，上述试验最少做一种，但是为了较为准确的 表达本构关系，应尽可能多的得到多种试验的数据[7]。
熟悉有限元软件 Abaqus、Marc、Adina、Hypermesh
确定分析对象， 直接在 分析对象上取橡胶材 料进行材料试验
单轴、等双轴、平面和体积试验
建立零件的三维模型
对三维模型进行有限 元网格划分
根据试验数据拟合材料 参数，并把材料参数赋 予有限元模型
根据试验数据，选出最能反映材料 特性的本构关系模型
根据实际情况， 确定模 型的载荷和边界条件， 提交模型进行有限元 计算
根据分析结果提出修 改意见
图 1 对橡胶件进行有限元分析流程图
单轴试验
等双轴试验
平面试验
体积试验 图2 确定本构关系所需试验类型
2）创建橡胶隔振件的有限元模型。
其中包括零件的三维建模、有限元网格划 分、输入材料特性、施加边界条件、计算分析及后处理[8]。
3）根据分析结果，提出结论和设计修改意见，再根据修改意见进行修改，重 新建立修改后的零件有限元模型，进行进一步的分析计算。
四、几个橡胶件的分析计算例子
1） 某发动机前悬置的有限元分析
图 3 发动机前悬置结构图
图 4 发动机前悬置有限元网格图
某重型商用车发动机前悬置三维结构模型如图 3 所示，悬置由三部分组成： 顶板、 内套、 橡胶软垫和外套。
其中内、 外套和顶板材料为合金钢。
Hypermesh 在 中对前悬置模型进行网格划分，单元类型为 8 节点六面体线性单元，有限元网格 模型如图 4 所示。
然后把网格模型导入有限元软件 ABAQUS，赋予金属和橡胶 的材料特性，并且赋予橡胶单元为杂交单元特性。
根据实际情况，在 ABAQUS 中对前悬置模型施加 1348N 的垂向力和 25N 的 侧向力，有限元模拟的垂向刚度与试验值的比较如图 5 所示，从图中可以看出， 模拟曲线与试验曲线比较相近，说明所建立的有限元模型是正确的。
前悬置垂向 位移云图以及橡胶软垫的 Mises 应力云图分别如图 6 和图 7 所示。
1600 1400 1200 1000 800 600 400 200 0 0 1 2 位移/mm
有限元模拟刚度曲线
试验刚度曲线
力/N
3
4
5
图 5 发动机前悬置垂向刚度模拟值与试验值比较
图 6 发动机前悬置位移云图
图 7 发动机前悬置橡胶软垫 Mises 应力云图
2）某发动机后悬置的有限元分析 发动机后悬置三维模型如图 8 所示，有限元模型如图 9 所示，上座和底座材 料为铸铁，弹性材料为橡胶。
有限元模型中单元类型为四面体单元，橡胶材料采 用杂交单元模拟。
图 8 发动机后悬置三维模型
图 9 发动机后悬置有限元模型
根据实际情况，对发动机悬置上座施加垂向力 3136N，垂向位移及橡胶主簧 Mises 应力分布如图 10 和图 11 所示。
所得悬置静刚度为 917N/mm，试验测得其 静刚度为 902N/mm，误差在 10%以内，说明所建立的有限元模型是正确的。
图 10 悬置垂向位移云图
图 11 橡胶软垫 Mises 应力云图
后悬置垂向位移云图及后悬置橡胶软垫应力云图如图 8 和图 9 所示
五、结论
利用有限元技术对橡胶件设计分析计算，在材料模型和边界条件确定精准的 前提下，计算精度较高，相对于试验方法，有限元方法周期短，成本低，适用于 产品研发的前期阶段。
参 考 文 献
[1] 李晓芳，杨晓翔. 橡胶材料的超弹性本构模型[J].弹性体,2005,15(1):50-58 [2] 梁 天 也 ， 史 文 库 ， 马 闯 . 汽 车 动 力 总 成 液 压 悬 置 橡 胶 主 簧 静 特 性 有 限 元 分 析 [J]. 振 动 与 冲 击,2007,26(9):155-157 [3] Twizell,E.H.,R.W.Ogden. Non-Linear Optimization of the Material Constants in Ogden’s Stress Deform-ation Function for Incompressible Isotropic Elastic Materials[J]. Austral. Math. Soc. Ser. B,1983,24:424-434 [4] Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber[J]. Rubber Chemistry and Technology,1993,66:754771 [5] Vilgis,Th., H. G. Kilian. The Van der Waals-network—A Phenomenological Approach to Dense Networks[J]. Polymer,1984,25:71-74 [6] ABAQUS Benchmarks Manual 6.5. SIMULIA Co.Ltd.2005 [7] 庄茁，由小川，廖剑晖 等.基于 ABAQUS 的有限元分析和应用[M]. 北京：清华大学出版社，2009： 253-254 [8] 王利荣，吕振华. 橡胶隔振器有限元建模技术及静态弹性特性分析[J]. 汽车工程,2002,24(6):480-485
。