弹性力学及有限元基础部分作业
《弹性力学及有限元》测验试卷

一、在建立弹性力学平衡微分方程、几何方程、物理方程时分别应用了哪些基本假定?
二、在什么条件下平面应力问题与平面应变问题的应力分量xy y x τσσ,,是相同的?
三、体力为零的单连体应力边界问题,设下列应力分量已满足边界条件。
试考察它们是否为
正确解答,并说明原因。
0,2,2)2(===xy y x y x τσσ
四、有限单元法中,位移模式应满足什么条件? 下列位移函数 2321x a y a x a u ++= 2321y b y b x b v ++=
能否作为三角形单元的位移模式? 简要说明理由。
)(,,)1(a
y
b x q b y q a x q
xy y x +-===τσσ
题六图
七、某结构的有限元计算网格如题七图(a )所示。
网格中两种类型单元按如题七图(b )所
示的局部编号,它们单元劲度矩阵均为
⎥⎥⎤⎢⎢⎡-----25.025.0025.025.0025.025.0025.025.0005.0000
5.0。
弹性力学及有限元法答案下载

弹性力学及有限元法答案下载一、是非题(下列各题,你认为正确的,请在题干的括号内打“√”,错的打“×”。
每题3分,共12分)1、按应力求解平面问题时,若应力分量满足平衡方程,且在边界上满足应力边界条件即为正确解答。
…………………………………………………………………………………………()2、图示弹性体在两种荷载作用下,若lh,则A点的应力分量是相同的。
…………………()3、用有限单元法求解平面应力问题时,单元刚度矩阵的子块kij的物理意义是:仅当第j个结点沿坐标正向发生x或y方向的单位位移,在i结点处引起的沿x或y 方向的结点力。
……()4、等厚度旋转圆盘以等角速度ω旋转时,该问题应属平面应变问题。
……………………()二、单选题(在本题的每一小题的备选答案中,只有一个是正确的,请把你认为正确答案的题号,填入题干的括号内。
多选不给分。
每题材5分,共15分)1、图示半平面体受集中力P作用,其应力边界条件为………………………………………()①θ=0,π,σθ=σr=0 ②θ=0,π,σθ=τθr =0③θ=0,π,r≠0,σθ=τθr=0 ④θ=0,π,r≠0,σθ=τθr=02、铅直平面内正方形薄板,边长为2a,周长固定,只受重力作用。
用瑞次法求解,其位移表达式应为…………………………………………………………………………………………()3、不计体力,图示弹性体的应力函数为………………………………………………………()①υ=τ0xy-(qy3)/6b ②υ=τxy+(qy3)/6b③υ=-τ0xy-(qy3)/6b ④υ=-τxy+(qy3)/6b三、填空题1、(3分)按应力求解平面问题。
若认应力函数υ=ax5y+bxy5(a、b 不等于零),则系数b、b应满足关系()。
2、(4分)已知一点应力状态为σx =100,σy=50,τxy=10,则σ1=(),σ2=()。
3、(3分)图示薄板,设其厚度t=1。
弹性力学与有限元法习题集

2019/7/29
slide4
返回
第二章习题与答案
1. 试说明弹性力学的基本假设?
2. 弹性力学平面问题的基本方程有哪三大类?各表征何种关系? 3. 虚功原理内容?
2019/7/29
slide5
答案 返回
4. 工程上具有什么特点的空间问题可以简化为平面应力问题? 5.工程上具有什么特点的空间问题可以简化为平面应变问题?
slide29
返回
4.题答案
解:
1 xi 1 Sijm 2 1 x j
1 xm
yi 1 4 1
1
yj
1 2
7
7 13.5
ym
11 4
2019/7/29
slide30
返回
5.题答案
1
Ni (x, y)x i N j (x, y)x j N m (x, y)x m 2 A [(ai x i a j x j am ym ) (bi x i b j x j bm x m )x
6. 应用几何方程推导应变分量应满足下列变形协调方程。
2 x 2 y 2 xy
y2 x2 xy
2019/7/29
slide6
答案 返回
7. 悬臂梁在三角形分布载荷作用下,可以看成平面应力问题,
应力分量表达式为, x
q 4a 3
x3 y
2xy3
6 5
a
y2)
Y 0
y
y
y
dy dx
( xy
弹性力学与有限元分析试题及其答案

如下图所示三角形薄板,按三结点三角形单元划分后,对于与局部编码ijm 对应的整体编码,以下叙述正确的是( D )。
① I 单元的整体编码为162 ② II 单元的整体编码为426③ II 单元的整体编码为246 ④ III 单元的整体编码为243⑤ IV 单元的整体编码为564A. ①③B. ②④C. ①④D. ③⑤一、填空题1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。
2、在弹性力学中规定,线应变以伸长时为正,缩短时为负,与正应力的正负号规定相适应。
3、在弹性力学中规定,切应变以直角变小时为正,变大时为负,与切应力的正负号规定相适应。
4、物体受外力以后,其内部将发生内力,它的集度称为应力。
与物体的形变和材料强度直接有关的,是应力在其作用截面的法线方向和切线方向的分量,也就是正应力和切应力。
应力及其分量的量纲是L -1MT -2。
5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。
6、平面问题分为平面应力问题和平面应变问题。
7、已知一点处的应力分量100=x σMPa ,50=y σMPa ,5010=xy τ MPa ,则主应力=1σ150MPa ,=2σ0MPa ,=1α6135' 。
8、已知一点处的应力分量, 200=x σMPa ,0=y σMPa ,400-=xy τ MPa ,则主应力=1σ512MPa ,=2σ-312 MPa ,=1α-37°57′。
9、已知一点处的应力分量,2000-=x σMPa ,1000=y σMPa ,400-=xy τ MPa ,则主应力=1σ1052 MPa ,=2σ-2052 MPa ,=1α-82°32′。
10、在弹性力学里分析问题,要考虑静力学、几何学和物理学三方面条件,分别建立三套方程。
11、表示应力分量与体力分量之间关系的方程为平衡微分方程。
12、边界条件表示边界上位移与约束,或应力与面力之间的关系式。
国科大有限元作业1
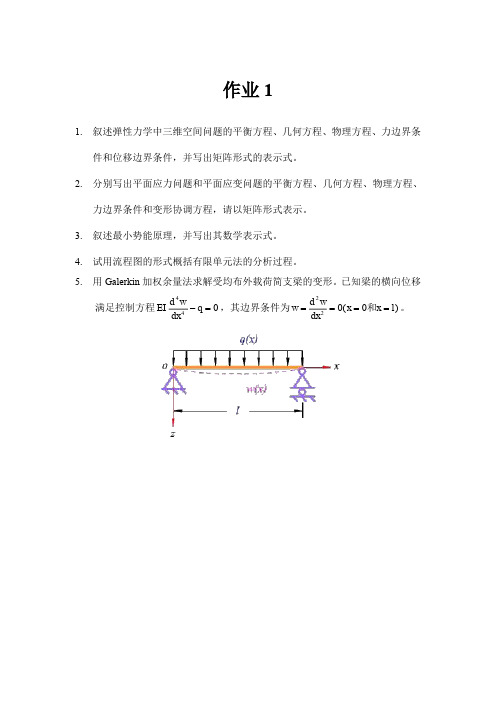
作业1
1.叙述弹性力学中三维空间问题的平衡方程、几何方程、物理方程、力边界条
件和位移边界条件,并写出矩阵形式的表示式。
2.分别写出平面应力问题和平面应变问题的平衡方程、几何方程、物理方程、
力边界条件和变形协调方程,请以矩阵形式表示。
3.叙述最小势能原理,并写出其数学表示式。
4.试用流程图的形式概括有限单元法的分析过程。
5.用Galerkin加权余量法求解受均布外载荷简支梁的变形。
已知梁的横向位移
满足控制方程
4
4
w
d
EI q
dx
-=,其边界条件为
2
2
0(0)
d w
w x x l
dx
====
和。
弹性力学与有限元分析试题及参考答案

按应力求解平面应变问题的相容方程:
将已知应力分量 , , 代入上式,可知满足相容方程。
4、试写出平面问题的应变分量存在的必要条件,并考虑下列平面问题的应变分量是否可能存在。
(1) , , ;
(2) , , ;
(3) , , ;
其中,A,B,C,D为常数。
弹性力学与有限元分析试题及参考答案
四、分析计算题
1、试写出无体力情况下平面问题的应力分量存在的必要条件,并考虑下列平面问题的应力分量是否可能在弹性体中存在。
(1) , , ;
(2) , , ;
其中,A,B,C,D,E,F为常数。
解:应力分量存在的必要条件是必须满足下列条件:(1)在区域内的平衡微分方程 ;(2)在区域内的相容方程 ;(3)在边界上的应力边界条件 ;(4)对于多连体的位移单值条件。
6、证明应力函数 能满足相容方程,并考察在如图所示的矩形板和坐标系中能解决什么问题(体力不计, )。
解:将应力函数 代入相容方程
可知,所给应力函数 能满足相容方程。
由于不计体力,对应的应力分量为
, ,
对于图示的矩形板和坐标系,当板内发生上述应力时,根据边界条件,上下左右四个边上的面力分别为:
上边, , , , , ;
解:应变分量存在的必要条件是满足形变协调条件,即
将以上应变分量代入上面的形变协调方程,可知:
(1)相容。
(2) (1分);这组应力分量若存在,则须满足:B=0,2A=C。
(3)0=C;这组应力分量若存在,则须满足:C=0,则 , , (1分)。
5、证明应力函数 能满足相容方程,并考察在如图所示的矩形板和坐标系中能解决什么问题(体力不计, )。
弹性力学及有限元习题参考答案(赵均海、汪梦甫)汇编

xy
x
xz
X 0
x
y
z
yx
y
yz
Y 0
x
y
z
zx
z
zy
Z 0
x
y
z
已知:
x
2f1
2f2
E(1 )
E
(
2A)
x (1 )(1 2)x2 (1 )(1 2) xy
τN =55.2Mpa;
习题 1.3
解:(1)应力不变量:
2 − 2 − 2
因为 I 1 = x + + ; I 2 = y + + −
将已知代入上式,得:I 1 = 25 MPa ,I 2 = −3250 MPa
(2)求主应力:
x −
y
2f2
2f1
E(1 )
E
(
2B)
y (1 )(1 2) y 2 (1 )(1 2) xy
z
z
0
xy
2f
2f2
E
( 21
)
y
(
2 1 ) x
xy
xz
0 , yz 0
z
z
+
z 2 z =
(1 )(1 2) (1 )
xy xy
E
xy
(
2 1 )
yz yz
E
yz
(
2 1 )
xz xz
有限元法基础习题答案

有限元法基础习题答案有限元法是一种常用的工程分析方法,广泛应用于结构力学、热传导、流体力学等领域。
它通过将复杂的物理问题离散化为一系列简单的子问题,并利用数值方法求解这些子问题,从而得到整体问题的近似解。
在学习有限元法的过程中,习题是必不可少的一环。
本文将给出一些有限元法基础习题的答案,希望能够帮助读者更好地理解和掌握这一方法。
习题一:一维线性弹性力学问题考虑一根长度为L的弹性杆,杆的截面积为A,杨氏模量为E。
在杆的一端施加一个沿杆轴向的拉力F,另一端固定。
假设杆轴向变形u(x)满足以下方程:EAu''(x) = -F,0 < x < Lu(0) = 0, u(L) = 0其中,u''(x)表示u(x)对x的二阶导数。
解答:根据上述方程,我们可以得到杆的位移函数u(x)的表达式。
首先,对方程两边进行积分,得到:EAu'(x) = -Fx + C1其中,C1为积分常数。
再次对方程两边进行积分,得到:EAu(x) = -F/2*x^2 + C1*x + C2其中,C2为积分常数。
根据边界条件u(0) = 0,可得C2 = 0。
代入边界条件u(L) = 0,可得:EAu(L) = -F/2*L^2 + C1*L = 0由此可得C1 = F/2*L。
将C1代入上式,可得:EAu(x) = -F/2*x^2 + F/2*L*x最终得到杆的位移函数u(x)的表达式为:u(x) = (-F/2*E)*(x^2 - L*x),0 < x < L习题二:二维平面弹性力学问题考虑一个正方形薄板,边长为L,板的厚度为h。
假设薄板的杨氏模量为E,泊松比为ν。
在薄板的一侧施加一个沿法向的均匀表面压力P,另一侧固定。
求薄板的位移和应力分布。
解答:根据平面弹性力学理论,我们可以得到薄板的位移和应力分布。
首先,根据杨氏模量E、泊松比ν和薄板的厚度h,可以计算出薄板的弹性模量D:D = E*h^3 / (12*(1-ν^2))接下来,根据薄板的边界条件和平衡方程,可以得到薄板的位移和应力分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 2 第10-6题图 解:本题只有三个结点,两个单元,计算结果应该是准确度不 会很高。 单元1的刚度矩阵 单元1的刚度矩阵
总刚度矩阵 载荷列阵为 为了消除总刚度矩阵的奇异性,利用乘大数法引入位移边 界条件,总刚度矩阵可以改写为 因此,位移列阵 于是,结点2和3处的位移和转角分别为 , , 10-7.如图 3所示薄板结构用四个三角形单元离散: i结 j结 m结 单元 点 点 点 A B C D 求结构的刚度矩阵。 1 3 2 1 4 4 3 3 3 5 5 2
Ke(2*jj-1:2*jj,2*kk-1:2*kk); end end end % 4.求解P矩阵 P=zeros(1,2*(n1+n2+1)); P(2*(n1+1))=P0; % 5.消除刚度矩阵奇异性 K=Kt; K(1,1)=K(1,1)*1e9; K(2,2)=K(2,2)*1e9; K(2*(n1+n2+1)-1,2*(n1+n2+1)-1)=K(2*(n1+n2+1)-1,2* (n1+n2+1)-1)*1e9; K(2*(n1+n2+1),2*(n1+n2+1))=K(2*(n1+n2+1),2*(n1+n2+1))*1e9; % 6.求解位移 a=(K\P')'; % 7.求解节点力 Pt=(Kt*a')'; % 8.求解节点应力 sigma_element=zeros(1,n1+n2); epsilon_element=zeros(1,n1+n2); B=[-1/2 sqrt(3)/2 1/2 -sqrt(3)/2]/Le1; for ii=1:n1 k=[ii,ii+1]; a_e(1:2)=a(2*k(1)-1:2*k(1)); a_e(3:4)=a(2*k(2)-1:2*k(2)); epsilon_element(ii)=B*a_e'; sigma_element(ii)=E*B*a_e'; end B=[-1/sqrt(2) -1/sqrt(2) 1/sqrt(2) 1/sqrt(2)]/Le2; for ii=n1+1:n1+n2 k=[ii,ii+1]; a_e(1:2)=a(2*k(1)-1:2*k(1)); a_e(3:4)=a(2*k(2)-1:2*k(2)); epsilon_element(ii)=B*a_e'; sigma_element(ii)=E*B*a_e'; end
10-4.图 1中所示钢索BC长600mm,BC和BD与铅垂线的夹角分别 为,在B点处沿竖直方向作用一集中力P=80kN,求B点的水平 方向和竖直方向的位移,点C和D处的支反力,单元节点力和 应力。钢索的弹性模量E=207GPa,截面面积。
图 1 第10-4题图 设BC钢索上某个单元内的两个结点的左边分别为,位移分 别为,那么该单元内的正应变的大小为 即 其中, 单位刚度矩阵为 同理BD钢索上某个单元内正应变的大小为 即 其中, 单位刚度矩阵为 由于BC钢索、BD钢索的内的应变均为常量,故将BC钢索 作为一个单元,BD钢索作为一个单元。可以利用如下的matlab 程序求得位移的大小以及相应的单元节点力,应力。
plot(B(1),B(2),'k.', 'Marker','.','MarkerSize',15) plot(D(1),D(2),'k.', 'Marker','.','MarkerSize',15) text(C(1)-30,C(2)-20,'C'); text(B(1)+20,B(2),'B'); text(D(1)+10,D(2)-20,'D'); text(B(1)+20,B(2)-200,'P','FontWeight','Bold'); text(C(1)-100,C(2)-100,'L_{BC}=600mm'); text(B(1)-100,B(2)+200,'\alpha=30^{。}'); text(B(1)+50,B(2)+180,'\beta=45^{。}'); plot([B(1),B(1)],[B(2),B(2)+200],'k-.'),hold on plot([B(1),B(1)],[B(2),B(2)-200],'k-','LineWidth',1.5),hold on arrow_P= [B(1),B(1)+8,B(1)-11;B(2)-200,B(2)-200+30,B(2)-200+30]; fill(arrow_P(1,:),arrow_P(2,:),'k') axis([-200,1000,-800,100]) theta=90:(120-90)/30:120; theta=theta*pi/180; r=100; x0=B(1); y0=B(2); x=x0+r*cos(theta); y=y0+r*sin(theta); plot(x,y,'k-'),hold on theta=45:(120-90)/45:90; theta=theta*pi/180; r=150; x0=B(1); y0=B(2); x=x0+r*cos(theta); y=y0+r*sin(theta); plot(x,y,'k-'),hold on box off
end BB=BB/D; Ke=conj(BB')*DD*BB*A; for jj=1:3 for kk=1:3 Kt((k(jj)*2-1):k(jj)*2,(k(kk)*2-1):k(kk)*2)=... Kt((k(jj)*2-1):k(jj)*2,(k(kk)*2-1):k(kk)*2)+... Ke((jj*2-1):jj*2,(kk*2-1):kk*2); end end end
B点是第2个结点,其位移大小为 C,D两点分别是第1个和第3个结点,由于没有力的加载 为,。 C,D两点的约束反力分别为, ,方向为沿各自钢索的方 向。 相应的正应力为,。 10-6.如图所示梁的结点2和3处的位移和转角。已知梁的弹性模 量为E,截面惯性矩。提示,梁的刚度方程为 其中,v为y方向位移,V为剪力,M为弯矩。
求得总刚度矩阵为令 图 1的matlab绘图指令
C=[0,0]; B=[600/2,-600*sqrt(3)/2]; plot([C(1),B(1)],[C(2),B(2)],'k-'),hold on axis equal D=[B(1)-B(2),0]; plot([D(1),B(1)],[D(2),B(2)],'k-'),hold on plot([C(1)-50,D(1)+50],[C(2),D(2)],'k-','LineWidth',2),hold on n=20; yinying=zeros(2,n+1); yinying(1,1:n+1)=(C(1)-50):((D(1)+50)-(C(1)-50))/n:(D(1)+50); yinying(2,1:n+1)=zeros(1,n+1); yinying(3,1:n+1)=yinying(1,1:n+1)+20*ones(1,n+1); yinying(4,1:n+1)=yinying(2,1:n+1)+20*ones(1,n+1); for ii=1:n+1 plot([yinying(1,ii),yinying(3,ii)], [yinying(2,ii),yinying(4,ii)],'k-'),hold on end plot(C(1),C(2),'k-', 'Marker','.','MarkerSize',15)
图 3 第10-7题图 解:对于某一单元 A是该单元的面积。 单元刚度矩阵 总刚度矩阵,代入诸 后可以得到 其中,t为厚度,E为杨氏模量,ν是泊松比 取h=40mm,w=100mm,E=200GPa,ν=0.32,t=1mm,可以利
用如下的matlab程序求解总刚度矩阵。
clc clear all E=200; % 杨氏模量 niu=0.32; % 泊松比 DD=[1,niu,0;niu,1,0;0,0,(1-niu)/2]; DD=DD*E/(1-niu^2); h=40; w=100; t=1; coord=conj([... 0 0;... 0 h;... w/2 h/2;... w 0;... w h ]'); nc=length(coord); element=[... 1 4 3;... 3 4 5;... 2 3 5;... 1 3 2 ]'; ne=length(element); for ii=1:ne k=element(1:3,ii)'; % 计算Ke x=coord(1,k(1:3)); y=coord(2,k(1:3)); b=[y(2)-y(3),y(3)-y(1),y(1)-y(2)]; c=[x(3)-x(2),x(1)-x(3),x(2)-x(1)]; D=det([1,1,1;x;y]); A=D/2; for jj=1:3 BB(1:3,(2*jj-1):2*jj)=[... b(jj) 0;... 0 c(jj);... c(jj) b(jj)];
clc clear all % 1.常量定义 E=207; A=120; L1=600; L2=L1*sqrt(3)/2*sqrt(2);
