薄膜力学-5-应力与曲率
结构力学(“弯矩”相关文档)共6张
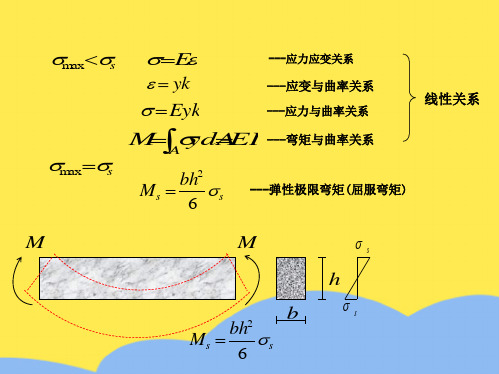
---塑性极限弯矩(简称为极限弯矩)
意 ---弹味性着极该限截弯面塑矩两(侧性屈可服铰以弯发与矩生)铰相对的转差角,别形:如一个铰链。
1.塑性铰可承受极限弯矩;
2.塑性铰是单向的;
3.卸载时消失; 4.随荷载分布而出现于不同截面。
k M 意味着该截面两侧可以发生相对转角,形如一个铰链。
塑性铰可承受极限弯矩;
u
s
---弹性极限弯矩(屈服弯矩)
处于弹性的部分称为弹性核.
k ---塑性极限弯矩(简称为极限弯矩意) 味着该截面两侧可以发生相对转角,形如一个铰链。
处意于味弹 着性该的截部面分两u称侧为可弹以性发核生相. 对称转角为,塑形如性一铰个铰。链。
塑性铰
若截面弯矩达到极限弯矩,这时的曲率记作 k u 。
ks 3 2 M
k
若截面弯矩达到极限弯矩,这时的曲率记作 。
Ms
M u 1.5 Ms
意味着该截面两侧可以发生相对转角,形如一个铰链。
塑性铰可承受极限弯矩;
k 32 M 0 -意--塑味性着极该限截弯面矩两(侧简可称以为发极生限相弯s对矩转) 角,形如一个铰链。 u
---弯矩与曲率关系
非线性关系
或 ks 3 2 M
k
Ms
Mu
bh2 4
s
M
---塑性极限弯矩(简称为极限弯矩)
M u 1.5 Ms
M
b
Ms
bh2 6
s
s s
h s s
s
y0 y0
s
处于弹性的部分称为弹性核. ---弹性极限弯矩(屈服弯矩) 意味着该截面两侧可以发生相对转角,形如一个铰链。 中意塑 塑-中处塑--意意-意中处塑意塑--------弹塑塑塑性味性性性于性味味味性于性味性性性性性轴 着 铰铰 轴 弹 铰 着 着 着 轴 弹 铰 着 铰极极极极附该可 可附性可该该该附性可该可限限限限近截承 承近的承截截截近的承截承弯弯弯弯处面受 受处部受面面面处部受面受矩矩矩矩于两极 极于分极两两两于分极两极((((弹侧限 限弹称限侧侧侧弹称限侧限屈简简简性可弯 弯性为弯可可可性为弯可弯服称称称状以矩 矩状弹矩以以以状弹矩以矩弯 为 为 为态发态性发发发态性发;;;;;矩极极极生核生生生核生...)限限限相相相相相..弯弯弯对对对对对矩矩矩转转转转转))) 角角角角角,,,,,形形形形形如如如如如一一一一一个个个个个铰铰铰铰铰链链链链链。。。。。 中性轴附近处于弹性状态. 意味着该截面两侧可以发生相对转角,形如一个铰链。 中性轴附近处于弹性状态.
薄膜应力测量研究现状

X Pe Zh g u ng an Me ng
(. 1南昌大学分析 测试 中心 ;2南 昌大学材料科学与工程学院 ,南昌 304) . 307
( .n l z n e t C n e o a c a g U i e s t ; 1 A a y e a d T s e t r f N n h n n v r i y
随着传统光及计算机技术、 真空技术、 光电子技术、 测 控 技术的飞速 发展 , 薄膜光学器件 以及薄膜 电子器件得到 了 日益广泛的应用。 但是薄膜应力的存在直接影响薄膜元器件 的成品率、稳定性和可靠性I 。因此,研究薄膜应力显得
一
1 1基 片变形法 . 沉积在基 片上薄膜 的应力会造成基片的弹性弯 曲, 过 通
在镀膜的过程中, 薄膜和基体的温度都 同时升高, 而在镀膜 后, 下降到初始温度时, 由于薄膜和基体的热膨胀系数不同, 便产生了内应力, 一般称之为热应力, 这种现象称作双金属 效应,但由这种效应引起的热应力不能认为是本质的论断。 薄膜热应力指的是在变温的情况下, 由于受约束的薄膜的热 胀冷缩效应而引起的薄膜内应力。 另一方面是薄膜生长过程 中的非平衡性或薄膜特有的微观结构引起的, 主要是指薄膜 在形成过程 中的 内应力, 也称为本征应力 。 本征应力又可分 为界面应力和生长应力。 界面应力来源于薄膜与基体在接触 界面处的晶格错配或很高的缺陷密度, 而生长应力则与薄膜 生长过程中各种结构缺陷的运动密切相关。 本征应力与薄膜 的制备方法及工艺过程密切相关, 且随着薄膜和基体材料的
式为
E。 t6
a j —— —
—
一
3I  ̄ t (- ) f o L 式中,E为基片的杨氏 模量 ;U为基片的泊松比;L 。 为 基片长度;t为基片厚度;t为薄膜厚度。 。
材料力学第五章弯曲应力

式中 : M 横截面上的弯矩
Iz
横截面对中性轴的惯性矩
y
求应力的点到中性轴的距离
I z A y2dA
m 惯性矩是面积与距离平方的乘积,恒为正值,单位为 4
My
IZ
讨论
应用公式时,一般将 M,y 以绝对值代入。根据梁变 形的情况直接判断 的正,负号。 以中性轴为界,梁 变形后凸出边的应力为拉应力( 为正号)。凹入边 的应力为压应力,( 为负号)。
max M (x) WZ
RA
P
A
C
5m 10m
RB B
a
12.5
z
166
例题1 :图示简支梁由 56 a 工字钢制成 ,其横截面见图 p = 150kN。求 (1) 梁上的最大正应力 max
(2) 同一截面上翼缘与腹板交界处 a 点的应力
解:
C 截面为危险截面。最大弯矩
+
M max 375KN.m
查型钢表,56 a 工字钢
I z 65586 cm6
W z 2342cm2
(1) 梁的最大正应力 +
σ max
M max WZ
160MPa
(2) a点的正应力
a点到中性轴的距离为
ya
560 2
21
所以 a 点的正应力为
σ a M max ya 145MPa IZ
12.5
My
IZ
最大正应力发生在横截面上离中性轴最远的点处 当 中性轴为对称轴时 ,ymax 表示最大应力点到中性轴 的距离,横截面上的最大正应力为
max M ymax Iz
WZ
IZ ymax
《材料力学》 第五章 弯曲内力与弯曲应力

第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁,火车的轮轴,楼房的横梁,阳台的挑梁等。
二、弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线。
变形特点——杆轴线由直线变为一条平面的曲线。
三、梁的概念:主要产生弯曲变形的杆。
四、平面弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线,且都在梁的纵向对称平面内(通过或平行形心主轴且过弯曲中心)。
变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。
五、弯曲的分类:1、按杆的形状分——直杆的弯曲;曲杆的弯曲。
2、按杆的长短分——细长杆的弯曲;短粗杆的弯曲。
3、按杆的横截面有无对称轴分——有对称轴的弯曲;无对称轴的弯曲。
4、按杆的变形分——平面弯曲;斜弯曲;弹性弯曲;塑性弯曲。
5、按杆的横截面上的应力分——纯弯曲;横力弯曲。
六、梁、荷载及支座的简化(一)、简化的原则:便于计算,且符合实际要求。
(二)、梁的简化:以梁的轴线代替梁本身。
(三)、荷载的简化:1、集中力——荷载作用的范围与整个杆的长度相比非常小时。
2、分布力——荷载作用的范围与整个杆的长度相比不很小时。
3、集中力偶(分布力偶)——作用于杆的纵向对称面内的力偶。
(四)、支座的简化:1、固定端——有三个约束反力。
2、固定铰支座——有二个约束反力。
3、可动铰支座——有一个约束反力。
(五)、梁的三种基本形式:1、悬臂梁:2、简支梁:3、外伸梁:(L 称为梁的跨长) (六)、静定梁与超静定梁静定梁:由静力学方程可求出支反力,如上述三种基本形式的静定梁。
超静定梁:由静力学方程不可求出支反力或不能求出全部支反力。
§5—2 弯曲内力与内力图一、内力的确定(截面法):[举例]已知:如图,F ,a ,l 。
求:距A 端x 处截面上内力。
解:①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力:剪力和弯矩1. 弯矩:M ;构件受弯时,横截面上存在垂直于截面的内力偶矩。
薄膜力学性能资料

th f TsTdT
(4.22)
根据Hooke’s定律,应力为
th
E
1 f
th
(4.23)
18
薄膜—基底体系中由于晶格常数失配在薄膜中产生的内 应力由Hoffman的晶界松弛模型得到
i
1
Ef
f
xa a
1
Ef
f
Lg
(4.24)
式中 a为薄膜材料为无残余应力时的晶格常数, x 为a由于
详细推导过程见流程图2。
15
表4.1 式(4.21)中对应于hg /R 的系数
16
17
图2 根据p-h 曲线确定应力-应变关系的流程图
4.2 薄膜的残余应力
一、残余应力的来源
通常认为,薄膜中的残余应力分为热应力和内应力两种 。
热应力是由于薄膜和基底材料热膨胀系数的差异引起的, 所以也称为热失配应力。热应力对应的弹性应变为
3
分类
脆性薄膜
按
脆性基底
力
学
性
质 分
脆性基底
韧性薄膜 韧性基底
4
4.1 薄膜的弹性性能
一、薄膜的弹性常数
弹性模量是材料最基本的力学性能参之一,由于 薄膜的某些本质的不同之处,其弹性模量可能完全不 同于同组分的大块材料。
5
三点弯曲
如图所示,加载和挠度的测量均在两支点中心位置,
对称压头载荷与压头深度之间的弹性解析分析,其结果
为
S dP dh
2
Er
A
(4.4)
这里,h为压头的纵向位移,S dP为d试h 验载荷曲线的薄
膜材料刚度, 是压A头的接触面积。
8
Er 为约化弹性模量
1
8 薄膜力学性能

薄膜力学性能
沈杰 复旦大学材料科学系
薄膜力学性能
附着力 薄膜厚度一般小于1微米,本身的机械强度导致其无法单独存在, 总要附着在各种基片上。 薄膜与基片之间的附着性能直接影响到薄膜的各种性能。 附着性差,薄膜无法使用。 应力 在制作过程中,薄膜结构受到工艺条件影响很大,薄膜内部因此 而产生一定的应力。 基片材料与薄膜材料之间热膨胀系数不同,也会使薄膜产生应力。 过大的内应力将使薄膜卷曲和开裂,导致失效。 硬度
复旦大学材料科学系
薄膜材料与器件
本征应力
热应力 本征应力:薄膜形成过程中由于缺陷等原因而引起的内应力。 本征应力与薄膜厚度有关。在薄膜厚度很薄时(10nm以下) ,构成薄膜 的小岛互不相连,即使相连也呈网状结构,此时的内应力较小。随着 膜厚的增加,小岛相互连接,由于小岛之间晶格排列的差异以及小孔 洞的存在,使内应力迅速增大,并出现最大值。膜厚进一步增加,并 形成连续膜时,膜中不再有小孔洞存在,此时应力减小并趋于稳定值。
复旦大学材料科学系
薄膜-基片界面
简单附着 (突变界面 ):薄膜与基片之间存在清 楚的分界面,相互作用为范德瓦尔斯力 扩散附着 (扩散界面 ):在薄膜和基片之间通过 基片加热、离子注入、离子轰击等方法实现原 子的互扩散,形成一个渐变界面,使薄膜与基 片的接触面积明显增加,附着力相应增加。 中间层附着 (复合界面 ):薄膜与基片之间形成 化合物中间层,薄膜通过中间层与基片形成牢 固的附着。 宏观效应附着: 机械锁合:基片表面的微观的凹凸、微孔 或微裂缝。在沉积薄膜时,部分原子进入 凹凸之中或微孔、微裂缝中,增加附着力。 双电层吸引:两种功函数不同的材料互相 接触时会发生电子转移,在界面两边聚集 起电荷,形成双电层,具有静电吸引能。 复旦大学材料科学系
材料力学第5章弯曲应力

M
M
中性轴
z
m
n
y
o
o
dA
z
mn
y
dx
Mzy
Iz
max
Mz Wz
M
MZ:横截面上的弯矩
y:到中性轴的距离
IZ:截面对中性轴的惯性矩
M
中性轴
§5-2 惯性矩的计算
一、静矩 P319
y
Sz ydA
A
z dA
zc
c y
S y zdA
yc
A
o
z
分别为平面图形对z 轴和 y 轴的静矩。
ySc Az ydA
F M
F
a
B
F
Fa
5.3 梁弯曲时的正应力
若梁在某段内各横截
面上的弯矩为常量, F
F
a
a
剪力为零, 则该段梁 A 的弯曲就称为纯弯曲。
B
Fs
在 AC 和 DB 段 内 横 截 面上既有弯矩又有剪 M 力, 这种情况称为横 力弯曲或剪切弯曲。
F F
Fa
平面假设
变形前原为平面的梁的横截面变形后仍保持为 平面, 并绕垂直于纵对称面的某一轴旋转, 且仍 然垂直于变形后的梁轴线。这就是弯曲变形的 平面假设。
C y'
a
x'
xc
b
注意!C点必须为截面形心。
六、组合截面的惯性矩
Iy Iyi
Iz Izi
例2:求对倒T字型形心 轴yC和zC的惯性矩。
解:1. 取参考轴yOz 2. 求形心
2cm y(yc)
1 c1
6 cm
yc
Ai yi A
y
c 1
用基片曲率法测量薄膜应力 - index 清华大学网络资源导 …

7 2 min Cu/ 1 min Ag
21
1. 67
25. 3 - 5. 8 - 436
8
2min Cu/ 1 min Ag (加偏压 - 200 V)
21
1. 67 - 22. 6 - 30. 2 23
注 :指每层对镀 1min Cu 和 0. 5min Ag ,其余相同 。
k0 , k ———分别为基片镀膜前后的曲率半径
Ms = Es/ (1 - vs) 为基片的二维杨氏模量 ,其中 Es , vs 分别 是基片材料的杨氏模量和泊松比 。
本实验中的 Si (111) 基片的二维杨氏模量为 229 GPa[5] 。在
硬基底软膜的情况下基片曲率法较为适用 。
1. 2 基片曲率法的种类
1 实验方法
1. 1 基片曲率法的原理
基片曲率法的原理是通过测量基片镀膜前后的曲率变化来
[ 收稿日期 ] 2003 - 02 - 18 [ 基金项目 ] 国家自然科学基金资助项目 (59971021)
计算薄膜应力 。该法要求基片为圆片状或长方条形 。当薄膜沉
积到基片上时 ,薄膜与基片之间产生二维界面应力 ,使基片发生
第 36 卷 第 7 期 2003 年 7 月
材 料 保 护 MATERIALS PROTECTION
Vol. 36 No. 7 July 2003
用基片曲率法测量薄膜应力
安 兵 ,张同俊 ,袁 超 ,崔 昆 (华中科技大学模具技术国家重点实验室 ,湖北 武汉 430074)
[摘 要 ] 采用基片曲率法设计和制作了一种测量薄膜应力的装置 ,它具有简单 、无损伤 、快速 、易于操作 、精度高的 优点 。使用该装置测量了射频磁控溅射镀制的 Cu 单层膜和 Ag/ Cu 多层膜的应力 ,结果表明薄膜残余应力是均匀的 ,但随 沉积条件不同而不同 。Cu 单层膜和 Ag/ Cu 多层膜处于压应力状态 ,外加 - 200 V 偏压时 ,Ag/ Cu 多层膜则转变为很小的拉 应力状态 。XRD 表明 Ag/ Cu 多层膜已结晶 ,呈现 Ag(111) / Cu(111) 择优取向 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[
]
= C02 + 2C01ε − 2C11κ + C00ε 2 − 2C10εκ + C 20κ 2
where
Cmn = ∫− hs / 2
hs / 2 + h f
M ( z )z [ε
m
f
( z )] dz
n
κ=
∂U ∂U = =0 ∂κ ∂ε
C11C00 − C01C10 2 C20C00 − C10
EM 397: Thin Film Mechanics
V. Film stress and substrate curvature
Nanshu Lu The University of Texas at Austin Fall 2013
Stoney formula
Assume hf << hs so that the film contribute negligibly to the overall stiffness. f f The membrane force f can be related to a residual stress or an excess surface stress.
Multilayer films
Mulitlayer films are common in engineering applications, for example, to achieve multi-functionality and reliability. The layers (films) are deposited sequentially, with different material properties and stresses. Question 1: What is the curvature subjected to stresses in multilayer films? Question 2: Can the stress in each film be measured by the wafer curvature method?
σ
a Neutral plane: Bending moment:
1 (1 + α )αβ a = hs 1 + 2 1 + αβ
σ
α=
hf hs
β=
Ef Es
1 1+α 1 M = σh f hs + h f − a = σh f hs 2 1 + αβ 2
κ0 =
6σh f
Ehቤተ መጻሕፍቲ ባይዱ
2 s s
is the curvature predicted by Stoney formula.
The error is less than 1% if hs/hf > 300, assuming Es = Ef .
When the film is relatively thick, the stress in the film is reduced due to bending, and the substrate is also stressed in this case. Examples include thermostatic bimetals and some MEMS structures.
Measuring film stress
Stoney formula: Plane stress: Plane strain: Equi-biaxial: (circular wafer)
M s = Es Es Ms = 2 1 −ν s Es Ms = 1 −ν s
6f κ= M s hs2
The curvature is independent of material properties of the film.
2 s s
• • • •
Mechanical method Capacitance method X-ray diffraction Optical methods
– – – – Scanning laser method Multi-beam optical stress sensor Grid reflection method Coherent gradient sensor (CGS)
CGS: non-uniform film stress by full-field curvature measurements?
Thick film or thin wafer
• Relax the assumption hf << hs • Consider a bilayer composite beam
C11C10 − C01C20 ε= 2 C20C00 − C10
Same results can be obtained by an equilibrium approach.
Thin multilayer films
h f = ∑ hi << hs
C10 ≈ 0
6σ i hi κ ≈ ∑κi = ∑ M s hs2
Superlattices: periodic mulitlayer films
• Quantum well lasers • Optical waveguides • Thermoelectric devices
Compositionally graded films
• Continuous variation in composition, microstructure, and residual strain through the thickness of the film
2 f M h Average film stress: σ= = s s κ hf 6h f
Measurements of wafer curvature
d w( r ) R= = 2 κ dr 1
2 −1
M h 1 1 σ= − 6h f R R0
R
h / 2+ h
Minimize the total strain energy to determine κ, ε1, and ε2. Note that the curvature now depends on the lateral dimension R.
Nonlinear spherical bending
M s hs2 σi = 6hi
1 1 − R R i −1 i
Geometrically nonlinear deformation
• The linear solution assumes axi-symmetrical bending with uniform curvature (spherical bending) • When deflection is large compared to the substrate thickness, geometrically nonlinear effects must be considered. • Materials remain linear elastic, and the strain is still small, but with relatively large rotation.
1 M = fhs 2
M 6f κ= = 2 Es I s Es hs
Assumptions and limitations
• Both hs and hf are laterally uniform and small compared to the lateral dimension; • hf << hs • The substrate material is homogeneous, isotropic, and linearly elastic • The film material is transversely isotropic (could be inelastic) • The film stress is laterally uniform • Edge effect is negligible • Strains and rotations are infinitesimal (linear thin-plate theory)
C 20 ≈ 1 3 M s hs 12
C11 ≈
hs 2
∑ M i ε i hi
i
• The total curvature equals the sum of the curvatures induced by each layer individually. • Stress in each film can then be measured from the curvature change during deposition or etching.
2
1 2 2 Strain energy density: U (r , z ) = M (z )ε1 − zκ + 3 ε + κ r + ε ( z ) 2 f 2
Total strain energy:
W = 2π ∫0 ∫− hss / 2 f U (r , z )dzdr
Freund, JMPS 48, 1159-1174 (2000).
S=K
S = K [1 + (1 − ν s ) K 2 ]
The linear solution becomes invalid for S > 0.3.
Curvature:
6σh f M 1+α κ= = Es I s + E f I f Es hs2 1 + 4αβ + 6α 2 β + 4α 3 β + α 4 β 2
