制作人程素君 第五章 角动量 关于对称性
普通物理学教程力学课后答案高等教育出版社第五章-角动量

第五章 角动量习题解答5.1.1 我国发射的第一颗人造地球卫星近地点高度d 近=439km,远地点高度d 远=2384km,地球半径R 地=6370km,求卫星在近地点和远地点的速度之比。
解:卫星在绕地球转动过程中,只受地球引力(有心力)的作用,力心即为地心,引力对地心的力矩为零,所以卫星对地心的角动量守恒m 月v 近(d 近+R 地)=m 月v 远(d 远+R 地)v 近/v 远=(d 远+R 地)/(d 近+R 地)=(2384+6370)/(439+6370)≈1.295.1.2 一个质量为m 的质点沿着j t b i t a r ˆsin ˆcos ωω+=的空间曲线运动,其中a 、b 及ω皆为常数。
求此质点所受的对原点的力矩。
解: 0)ˆsin ˆcos (ˆsin ˆcos /ˆcos ˆsin /222222=⨯-=⨯=-==-=+-=--==+-==r r m F r rm a m F r j t b i t a j t b i t a dt v d a j t b i t a dt r d v ωτωωωωωωωωωωωωω5.1.3 一个具有单位质量的质点在力场j t i t t F ˆ)612(ˆ)43(2-+-= 中运动,其中t 是时间。
该质点在t=0时位于原点,且速度为零。
求t=2时该质点所受的对原点的力矩。
解:据质点动量定理的微分形式,)1()(===m v d v m d dt Fdt j t i t t v d ]ˆ)612(ˆ)43[(2-+-=∴kk k k ij k j i j j i i j i j i F r j i j i F ji j i r j t t i t t r dt t t j dt t t i r d dtj t t i t t dt v r d jt t i t t v dt t j dt t t i v d r t t t t v ˆ40)ˆ(44ˆ18)2(ˆˆˆ,ˆˆˆ,0ˆˆˆˆ)ˆ18ˆ4()ˆ4ˆ()2()2()2(ˆ18ˆ4ˆ)6212(ˆ)2423()2(ˆ4ˆˆ)2322(ˆ)22()2(ˆ)32(ˆ)()(ˆ6)2(ˆ]ˆ)(6ˆ)2[(ˆ)(6ˆ)2()612(ˆ)43(ˆ343423423332441233324410002232232230020-=-⨯+⨯-=∴-=⨯=⨯=⨯=⨯+⨯+-=⨯=+=-⨯+⨯-⨯=+-=⨯-⨯+⨯-⨯=-+-=-+-=-+-==-+-=-+-=⎰⎰⎰⎰⎰⎰ττ5.1.4地球质量为6.0×1024kg ,地球与太阳相距149×106km ,视地球为质点,它绕太阳做圆周运动,求地球对于圆轨道中心的角动量。
力学(专)第五章 角动量-关于对称性

fi外 fi内 =
i
dLi dt
因对O点的力矩为:
r1
f12
r1 r2
r2 f21 f12
r12r1f1f2120r2
f12
故,
ri
f i内=0
i
15
ri
f i内=0
i
即:质点系的内力矩的矢量和为零;另一种定性解
释:如图示,
r1
f12
是以
f12
为底,高为
因此, Mo Z MZ
Mo'
r'F
o'o
r
F
o' o
F
r
F
r
F
Mo F Z
MZ
F
结论:力 F对Z 轴的力矩等于力 F对Z 轴上任意一点的力矩在Z轴上的投影。
4
2.一般情况
F F F// ,
MZ F MZ F
Mo
F
r
F
r
F//
r
F
r
F
Mo
F
MZ
dLZ dt
(6)
若 MZ 0,则:LZ C 恒量 (7) 质点对轴的角动量守恒定律
当然:由(4)式
M
dL
dt
Mx
dLx dt
M
y
dLy dt
Mz
dLz dt
(8)
11
例如:
1.质点受弹簧的拉力是一有心力,该力对力心的力矩为零,则质点对 该力心的角动量守恒;但换为另一点时,角动量不一定守恒。
i
i
i
又
MiZ 0 MiZ内 0
i
i
因此,
MiZ外
弹性力学基础(程尧舜_同济大学出版社)课后习题解答

WORD 格式.整理版图2.4习题解答第二章2.1计算:(1)pi iq qj jk δδδδ,(2)pqi ijk jk e e A ,(3)ijp klp ki lj e e B B 。
解:(1)pi iq qj jkpq qj jk pj jk pk δδδδδδδδδδ===;(2)()pqi ijk jkpj qk pk qj jk pq qp e e A A A A δδδδ=-=-;(3)()ijp klp ki ljik jl il jk ki lj ii jj ji ij e e B B B B B B B B δδδδ=-=-。
2.2证明:若ijji a a =,则0ijk jk e a =。
证:20ijk jk jk jk ikj kj ijk jk ijk kj ijk jk ijk jk i e a e a e a e a e a e a e a ==-=-=+。
2.3设a 、b 和c 是三个矢量,试证明:2[,,]⋅⋅⋅⋅⋅⋅=⋅⋅⋅a a a b a cb a b b bc a b c c a c b c c证:1231112123222123333[,,]i i i i i i i i i i i i i i i i i i a a a b a c a a a a b c b a b b b c b b b a b c c a c b c c c c c a b c ⋅⋅⋅⋅⋅⋅=⋅⋅⋅==a a a b a c b a b b b c a b c c a c b c c 。
2.4设a 、b 、c 和d 是四个矢量,证明:()()()()()()⨯⋅⨯=⋅⋅-⋅⋅a b c d a c b d a d b c证:()()i j ijk k l m lmn n i j l m ijk lmk a b e c d e a b c d e e ⨯⋅⨯=⋅=a b c d e e ()()()()()i j l m il jm im jl i i j j i i j j a b c d a c b d a d b c δδδδ=-=- ()()()()=⋅⋅-⋅⋅a c b d a d b c 。
理论力学简明教程第五章答案

第五张 刚体力学平动中见彼此,转动中见分高低.运动美会让你感受到制造的乐趣.走过这遭,或许会有曾经沧海难为水的感叹.别忘了,坐标变换将为你迷津救渡,同时亦会略显身手.【要点分析与总结】1 刚体的运动(1)刚体内的任一点的速度、加速度(A 为基点)A r υυω'=+⨯()()A d r a a r dtωωω'⨯'=++⨯⨯ (2)刚体内的瞬心S :()21s A A r r ωυω=+⨯〈析〉ω为基点转动的矢量和,12ωωω=++A r r r '=+dr dtυ=*A A A dr dr d r r r dt dt dt υωυω''''=+=++⨯=+⨯ ()A d r d d a dt dt dtωυυ'⨯==++()r ωω'⨯⨯ 值得注意的是:有转动时r '与r ω'⨯的微分,引入了r ω'⨯与()r ωω'⨯⨯项。
2 刚体的动量,角动量,动能 (1)动量:c P m υ=(2)角动量: x x xx xy xz i i i y yxyy yz y zx zyzz z z L J J J L r m L J J J J J J J L ωυωωω⎛⎫⎛⎫⎛⎫-- ⎪ ⎪⎪=⨯===-- ⎪ ⎪ ⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎝⎭∑式中:转动惯量()()()222222xx yy zz J y z dmJ z x dm J x y dm ⎧=+⎪⎪=+⎨⎪=+⎪⎩⎰⎰⎰惯量积xx yy zz J xydm J yzdm J zxdm ⎧=⎪⎪=⎨⎪=⎪⎩⎰⎰⎰且c c cL r m L υ'=⨯+* l e 方向(以l 为轴)的转动惯量:(),,l l J e J e J ααβγβγ⎛⎫ ⎪== ⎪ ⎪⎝⎭222222xx yy zz yz zx xy J J J J J J αβγβγγααβ=++---(,,αβγ别离为l e 与,,x y z 轴夹角的余弦) * 惯量主轴惯量主轴能够是对称轴或对称面的法线若X 轴为惯量主轴,那么含X 的惯量积为0,即: 0==xy xz J J 若,,x y z 轴均为惯量主轴,那么:xx yy zz L J i J j J k =++ 〈析〉成立的坐标轴轴应尽可能的是惯量主轴,如此会降低解题繁度。
角动量.pdf

i
r ∑ mi ri′
i
与 i 无关
M
r × vC
由
r ∑ mi ri M
r ∑ mi ri′ M
∑
i
r r r r ri ′ × m i v c = M rc′ × v c = 0
质心对自己的位矢
r r r r r r r L = rc × ∑ mi vi + ∑ ri′× mi vc + ∑ ri′× mi vi′
r p1
i i i
r r r ri = rc + ri′ Q r r r v i = v c + v i′
有':对质心 无':对参考点
rr r r1rc r 2
r cp2
r ri′ θ θ
rr p pii
∴
与i无关
r r r r L = ∑ (rc + ri′) × m i v i
i i i
*质点对某参考点的角动量反映质点绕该参考点旋 转运动的强弱。 转运动的强弱。 *必须指明参考点, 必须指明参考点,角动量才有实际意义。 角动量才有实际意义。
2. 质点系角动量
r r r r r r L = ∑ Li = ∑ ri × pi = ∑ ri × mi vi
系统内所有质点对同一参考点 系统内所有质点对同一参考点角动量的矢量和 同一参考点角动量的矢量和
J = ∫ r 2dm 积分元选取: 积分元选取:
λdl
J = ∫ r dm
2
线密度: 线密度: λ , 线元: 线元: d l
面密度: 面密度: σ , 面元: 面元: dS
体密度: 体密度: ρ , 体元: 体元: dV
第5章角动量关于对称性

对质点,合力对某一参考点的力矩等于各分力
对同一参考点力矩的矢量和,如本题. 对O点
π M T rO FT sin ( ) 2 mg mg rO cos mgr cos M 合 rO F sinπ 0 M合 rO F M合 M重 MT
若
Mi外z 0
Lz ri mi vi sin i 常量
若质点系各质点绕 z 作圆周运动
Lz ri m i v i m i ri i
2
讨论
若Lz 不变,ri ,i
ri ,i
例如茹可夫斯基凳,花样滑冰等.
实例分析
[例题]装置如图所示.滑轮两边悬挂的重物与盘的质量相
§5.1.4质点对轴的角动量定理和守恒定律
1. 质点对轴的角动量定理 质点对参考点O的角动量
dL M dt
过参考点O建立坐标轴,则上式在 z 轴上的投影为
dLz Mz dt
称质点对 z 轴的角动量定理的微分形式.
z
2. 力对轴的力矩
F
F2
F1
如图所示:作平面与z轴垂直
F F1 F2
§5.2 质点系的角动量定理 及角动量守恒定律
§5.2.1 质点系对参考点的角动量定理及守恒律 §5.2.2 质点系对轴的角动量定理及守恒律
§5.2质点系的角动量定理 及角动量守恒定律
§5.2.1质点系对参考点的角动量定理及守恒律
1.质点系对参考点的角动量 对参考点
L Li ri pi ri mi vi
z
F2
力矩在 z 轴上的投影为
F
F1
r2
第五章角动量、关于对称性
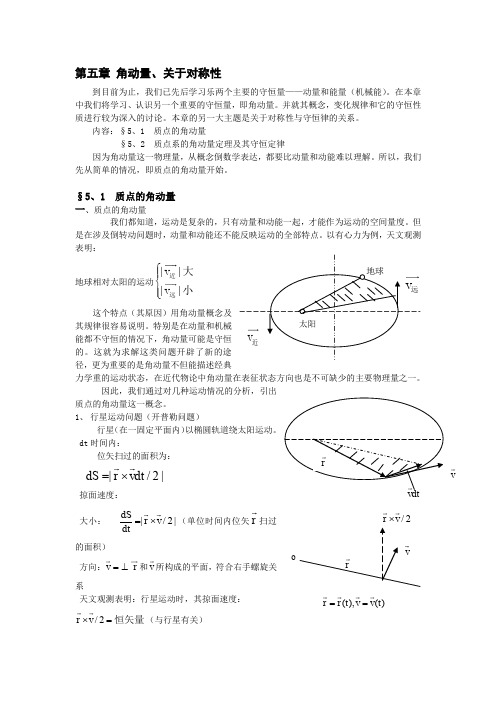
第五章 角动量、关于对称性到目前为止,我们已先后学习乐两个主要的守恒量——动量和能量(机械能)。
在本章中我们将学习、认识另一个重要的守恒量,即角动量。
并就其概念,变化规律和它的守恒性质进行较为深入的讨论。
本章的另一大主题是关于对称性与守恒律的关系。
内容:§5、1 质点的角动量 §5、2 质点系的角动量定理及其守恒定律因为角动量这一物理量,从概念倒数学表达,都要比动量和动能难以理解。
所以,我们先从简单的情况,即质点的角动量开始。
§5、1 质点的角动量 一、质点的角动量我们都知道,运动是复杂的,只有动量和动能一起,才能作为运动的空间量度。
但是在涉及倒转动问题时,动量和动能还不能反映运动的全部特点。
以有心力为例,天文观测表明:地球相对太阳的运动||||v v ⎧⎪⎨⎪⎩近远大小这个特点(其原因)用角动量概念及其规律很容易说明。
特别是在动量和机械能都不守恒的情况下,角动量可能是守恒的。
这就为求解这类问题开辟了新的途径,更为重要的是角动量不但能描述经典力学重的运动状态,在近代物论中角动量在表征状态方向也是不可缺少的主要物理量之一。
因此,我们通过对几种运动情况的分析,引出质点的角动量这一概念。
1、 行星运动问题(开普勒问题) 行星(在一固定平面内)以椭圆轨道绕太阳运动。
dt 时间内:位矢扫过的面积为:|/2|dSr vdt =⨯掠面速度: 大小: |/2|dSr v dt=⨯(单位时间内位矢r 扫过的面积)方向:v =r ⊥和v 所构成的平面,符合右手螺旋关系天文观测表明:行星运动时,其掠面速度:/2r v ⨯=恒矢量(与行星有关)vdt r vv vr/2r v ⨯v(),()r r t v v t ==讨论:①方向不变说明,轨道总在一固定平面内。
(由r v 和所构成) ②行星的动量和动能都不守恒,但有心力是保守力,故机械能守恒。
2、如图所示:橡皮筋一端固定于O 处,另一端与滑物块相系。
角动量与对称性

讨论张力和重力的力矩
三、力对点的力矩与对轴的力矩之间的关系
质点对点的角动量定理及其守恒定律
作用在质点上的合外力对参考点的力矩等于
此为角动量定理的积分形式(也称冲量矩定理)
质点对某轴的角动量对时间的变化率等
平面内的分量亦即质点角动量与Z轴存在一个夹角,我们可将其在
质点系对轴的角动量定理及其守恒定律我们考虑几个质点均分别在与Z轴垂直平面内运动,
考虑到前面已经证明成对出现的内力对参考点力
)
5.2.5轴的角动量对时间的变化率等于质点
轴的力矩之和始终为
在质心参照系中观察,各质点除受常力外,尚有惯性力
当运动速度远小于光速时,经典力学适用。
可将经典在经典力学中,物质的粒子性、波动性截然分开,量子力学以为在一些条件下粒子性是主要的,在另一些
当表征质点(粒子)的某些量(如角动量)远远大于普朗克常量时,可以用经典力
)相比时经典力学要让位于量子力学;
在量子力学中,粒子的能量、角动量均取分立值(经典力学中取连续值),速度与坐标不能同时确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、质点对参考点的角动量定理和守恒定律
● 质点的角动量定理 dL d dr d (mv ) = (r × mv ) = × mv + r × dt dt dt dt d (mv ) = r× (为什么 ?) dt
于是
dL dL = r×F ⇒ τ = dt dt
上式表明,在惯性系中,作用在质点上的合力对某参考点的力 在惯性系中,
都不守恒,却遵从角动量守恒定律,这就为求解这类运动问题 都不守恒,却遵从角动量守恒定律, 开辟了新途径。 开辟了新途径。
角动量不但能描述经典力学中的运动状态,在近代物理理 论中仍然是表征微观运动状态的重要物理量,例如原子核的角 动量,通常称为原子核的自旋,就是描写原子核特性的。 角动量守恒定律和动量守恒定律一样,是自然界最基本最
二、力对一参考点的力矩
动量定理说明,引起动量改变的原因是力;下面将看到, 引起角动量改变的原因是力矩。 对于力矩的概念,虽然在中学物理课中已作过初步介绍,
Hale Waihona Puke 例如,推门时作用力对门轴有力矩,用扳手拧螺帽时作用力对 螺杆的轴有力矩等,但那里讨论的只是物体绕一定轴线转动, 所遇到的力矩总是对轴的力矩,是力矩的一种特殊形式,力矩 的普遍定义是对一定参考点的,对轴的力矩只是对点的力矩沿 轴线的一个分量,下面将给出力矩的一般定义。 z F 如右图所示,O 是空间一点,F 是作 用力,A 表示受力点,受力点相对于 τ 受力点相对于 φ 参考点O 参考点 的位置矢量 r 与力 F 矢量的 矢量积τ 对参考点O的力矩 的力矩, 矢量积 叫做力 F 对参考点 的力矩, r A y x 其数学表达式为τ= × 其数学表达式为 r× F O 由定义可知,同一个力对于不同的参考点有不同的力矩, 因此讲到力矩时必须指明是相对哪一点而言的。当力 F不为零 时,力矩τ仍可能为零,这有两种情况:一是力的作用点就在参 考点 O ,此时位置矢量 r =0;另一种是沿力的方向的延长线通 过参考点 O ,此时sinφ=0 。如果质点在运动中受到的力始终 指向某个固定的中心,这种力叫做有心力,该固定点称为力 指向某个固定的中心,
m1 ac
x′
x O (a)
z′
m1
y′
y
z′
− m1ac
C
mn
mi
x′
C
mi − mn ac
(b)
y′
ma
− mi ac
图(b)即表示质心参考系中的情况,诸质点相对 C 系的 角动量用 L′ 表示,又用 ∑ τ i′外 表示作用于各质点诸力对 C 点 外力矩的矢量和。此外,所有质点各受惯性力 − mi ac ,根据
z L r O x (a) y mv φ
z
L′ α ′L′ z
o′
Lα
r′
Lz
mv ϕ
s
r
o (b)
应当指出的是,虽然质点相 对于任一直线(例如 z 轴) 上的不同参考点的角动量是 不相等的,但是这些角动量 在该直线上的投影却是相等 的。如图(b)所示,取 S 平 面与 z 轴垂直,则质点对于o 点及 o′点的角动量分别为 L
§5 对称性 • 对称性与守恒律
一、关于对称性
在远古不同的文化里都有对称的观念,以后又渗透到各种不 同的人类活动之中,包括绘画、雕塑、音乐、文学、建筑等等。
dLi dL ⇒ ∑ τ i内 + ∑ τ i外 = ∑ i dt dt
L 表示质点系内各质点对于参考点 O 的角动量的矢量和,叫 的角动量的矢量和, 做质点系对 O 点的角动量,根据牛顿第三定律,质点系的内 力总是成对出现,每一对内力的大小相等,方向相反,作用在 同一直线上,因此它们对同一参考点的力矩的矢量和为零,只 有外力矩有贡献。这样,求和方程变为
上述三个典型例子意味着对选定的参考点的角动量守恒。 我们把质点对 z 轴上任一点的角动量 L 在 z 轴上的投影,叫 质点对 轴上的投影, 轴的角动量, 表示,上面已证明, Lz的数值是 做质点对于 z 轴的角动量,用 Lz 表示 与参考点无关的。
y
[例题] 质量为 m 的质点在 xy 例题]
平面内以速度 v 作匀速直线运动, 如图所示,求此质点相对于原点 O 的角动量。 [解] 根据角动量的定义式 L = r × mv ,
● 质点角动量守恒定律
dL 根据质点角动量定理 τ = ,如果 τ = 0,则 L = 常量 dt 即作用于质点的合力对参考点O的力矩始终为零,则质点 的力矩始终为零, 对该点的角动量保持不变,称为质点对参考点 O 的角动量守恒 对该点的角动量保持不变, 定律。
角动量守恒定律是物理学中最基本的定律之一,和动量守恒定 律一样,它不仅适用于宏观物体的运动,而且对于牛顿第二定律不 能适用的微观粒子的运动,它也适用。
质点对轴的角动量定理和守恒定律(自阅) 四、质点对轴的角动量定理和守恒定律(自阅)
§3 质点系的角动量定理及角动量守恒定律
一、质点系角动量定理
设质点系由 N 个质点组成,对选定的某固定参考点,第 i 个 质 点的角动量定理的表达式为
dLi τi = dt
于是
令
τ i内 + τ i外 =
L = ∑ Li
v 因在平面内运动,故 r × = 恒矢量 2
● 橡皮筋实验,掠面速度亦为一恒量 ● 质点匀速直线运动,对线外任一点掠面速度守恒 上述不同的运动有共同特征,即 r × v 2 = 恒矢量 ,(运动 学量),能否对它们提供统一的动力学描述? 前两种运动的动量、动能均发生变化, 后一种动量、动能 均守恒。因此,动量和动能都不是对上面现象作出统一描述的 物理量。研究上述问题总需要选择参考点,对于一矢量,常可 对于一矢量,
dL τ= ,再考虑诸质点所受惯性力的力矩,即得 dt
dL′ ∑ τ i′外 + ∑ ri′× (−mi ac ) = dt 式中惯性力矩又可写作 ∑ mi ri′) × ma ⇒ ∑ τ ′ = dL′ − (∑ mi ri′) × ac = −( c i外 m dt
此即质点系对质心的角动量定理,与惯性系中角动量定理具有完 全相同的形式。是表明质心系特殊和重要性的又一个例子。
与 L′ , L 和 L′ 分别等于以 r 及 mv 为邻边及以 r ′ 及mv为邻边的平 行四边形的面积, L 与 L′ 在 z 轴上的投影分别是 Lz = L cos α
′ 和 L z = L ′ cos α ′(α 与 α ′分别是 L 与 L′和 z轴间的夹角 ) ,由图 ′ L (b)可见, z 和 Lz分别是相应的两个平行四边形在 S 面上的投 ′ 影面积,两者是相同的,故 Lz = Lz
普遍的定律之一。由于角动量这个物理量,从概念到数学表达, 都比动量要难理解,我们循序渐进逐步深入地来理解。 本章还要触及对称性的概念,尽管经典力学中的对称性没 有在微观领域中那么重要,但是介绍一下与本课水平相当的对 称性问题是十分有益的。
二、本章的基本要求
1. 理解质点及质点系角动量的物理意义; 2. 掌握质点、质点系的角动量定理; 3. 掌握角动量守恒定律; 4. 理解对称性的概念,了解守恒律与对称性的关系。
dL (1) ∑ τ i外 = dt 即质点系对于参考点O的角动量随时间的变化率等于各质点 所受外力对该点力矩的矢量和,称为质点系对参考点O的角动量 所受外力对该点力矩的矢量和, 定理。
这个定理告诉我们质点系的角动量随时间的变化率只决定
于质点系所受外力矩的矢量和,而与内力矩无关。内力矩只能 使系统内各质点的角动量改变,但不能改变质点系总的角动量。 在直角坐标系中,上式沿三个坐标轴的投影式为
三、本章的思考题及练习题
1.思考题:教材P164-165 2.练习题:5.1.2 5.1.7 5.1.8 5.1.9 5.2.2
§2 质点的角动量
一、质点的角动量
角动量的概念是怎么引出来的?三个重要的例子(教材第 149页) ● 行星绕太阳公转时,掠面速度守恒
1 1 r × dr r × v dt ds 1 2 2 = = = r × v = 常量 dt dt dt 2
§1 前 言
一、本章的基本内容及研究思路
角动量概念的建立和转动有密切联系,在研究物体的运动 时,人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况,并且在这类运动中也存在着某些共同的重要规律。例 如,天文观测表明,行星绕日运动遵从开普勒第二定律,在近 日点附近绕行速度较快,远日点速度较慢,这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
O′ d O
m
φ v
r
x
设 k 为沿 z 轴的单位矢量,则质点的角动量为
L = r × m v = − rmv sin φ k r 即 L 指向 z 轴负方向。由上图可以看出, sin φ 正好等于 O 点
与轨道的垂直距离 d ,因此代入上式得
L = −mvd k
由上例可以看出,并非质点仅在圆周运动时才具有角动量, 质点作直线运动时,对于不在此直线上的参考点也具有角动量。 另外,还可以看出,如果把参考点选在该直线上,则 sin φ = 0, 质点对该点的角动量永远等于零。因此,当谈到角动量时,必 须指明是对哪个参考点而言的,否则没有意义。
当∑τ iz = 0时,
Lz = 常量.
§4 质点系对质心的角动量定理和 守 恒 定 律
前面给出的角动量定理和角动量守恒定律都相对于惯性系 而言,现在研究质心参考系中质点系角动量的变化规律。如图 (a),C − x′y′z′ 即质心参考系。C 为质心, 和 z ′ 坐标轴
与惯性参考系 O − xyz 的 x, y 和 z 轴总保持平行,而质心具有 加速度 ac 。 z
心,上述第二种情况,有心力相对于力心的力矩恒为零。 力对 O 点的力矩τ 在通过 O 点的任一轴线如 z 轴上的分量, 叫做力对轴线 z 的力矩,用 τz 表示,这就是中学物理课中给出 的力矩的定义。正如上面对于角动量的讨论一样,力 F对于轴 线 z 上任一点的力矩τ 在该轴线上的分量的数值 τz 是与所选参 考点无关的。
