浙江省严州中学2015届高三3月阶段测试数学(文)试题
浙江省严州中学2015届高三3月阶段测试语文试卷.pdf

一、语言文字运用(共24分,其中选择题每小题3分) 1.下列词语中,加点的字注音全都正确的一组是 A.叨(dāo)扰 脚踝(huái) 乌桕(jiù)树 舐(shì)犊情深 B.怄(òu)气 重创(chuān) 配给(jǐ)制 煽(shàn)风点火 C.楔(xiē)子 绷(běn)脸 文绉(zōu)绉 方枘(ruì)圆凿 D.泠(lín)然 饯(jiàn)别 嚼(jiáo)舌头 封妻荫(yìn)子 2.下列各句中,没有错别字的一项是 A.一个人着装时不拘礼节可能表示你对交流沟通的另一方的漠视,肮脏的牛仔裤与笔挺气派的西装会给人以截然不同的印象。
B.雷军说在45岁生日当天他收到了两份大礼,一份是360投资结盟酷派,另一份是华为发布荣耀6plus,“这个行业的竞争恐怖得一踏糊涂”。
C.他的这一番关于“文明之旅”栏目的评价听起来很有见地,其实也不过是拾人牙惠罢了,根本没有一点自己的东西。
D.记者从省文联获悉,由文化部、中国文联、中国美协共同主办的“第十二届全国美术作品展览暨中国美术创作奖、获奖题名作品展”15日在中国美术馆开幕。
3.下列各句中,加点的词语运用正确的一项是 A.在刚结束的国王对阵湖人的比赛中,湖人队普莱斯在第一节开局时像巅峰时期的科比附体一样,单节得到14分,让对位的韦斯特布鲁克显得相形见绌。
B.在父亲的熏染下,小莫扎特在音乐方面的才华日益展露,经常为学校的活动创作曲谱,受到师生的追捧,但在老莫扎特看来这完全不值一提。
C.说完,他就转过身去,把被教训得一怔一怔的顾眉撂在屋子里,径自向外走去。
D.中国铁路总公司称,自2014年12月1日起火车票预售期将逐步延长至60天,消息一出,深受买票之苦的旅客无不奔走呼号。
4.下列各句中,没有语病的一项是 A.孩子们对“动漫”的情有独钟,推动着“动漫”产业朝着高质量、高速度、高赢利发展,嗅觉灵敏的商家对此更是起着推波助澜的作用。
浙江省严州中学2015届高三4月阶段测试数学(文)试题 Word版含答案

严州中学2015届高三4月阶段测试数学(文科)试卷试卷Ⅰ一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知,a b 为正实数,则“1a >且1b >”是“1ab >”的( ▲ ) A.必要不充分条件 B.充分不必要条件C.充分必要条件D.既不充分也不必要条件 2.下列函数中既是奇函数又是增函数的是( ▲ )A. 3y x x =+B. log a y x =C.3xy = D.1y x=-3.若,,l m n 是互不相同的空间直线,,αβ是不重合的平面,则下列命题正确的是( ▲ ) A. //,,//l n l nαβαβ⊂⊂⇒ B. ,l l αβαβ⊥⊂⇒⊥C. ,//l n m n l m ⊥⊥⇒D. ,//l l αβαβ⊥⇒⊥4.将函数cos(2)y x ϕ=+的图像沿x 轴向右平移6π后,得到的图像关于原点对称,则ϕ的 一个可能取值为( ▲ ) A.3π-B.6π C.3π D.56π 5.若直线20(0,0)-+=>>ax by a b 被圆224410++--=x y x y 所截得的弦长为6,则23+a b的最小值为( ▲ ) A. 10 B. 426+ C. 526+ D. 46 6.在ABC ∆中,若1AB =,3AC =,AB AC BC +=,则AB BC BC⋅=( ▲ )A. 32-B.12-C. 12D. 327. 已知∈a R ,若函数21()|2|2=--f x x x a 有三个或者四个零点,则函数2()41=++g x ax x 的零点个数为( ▲ ) A. 1或2 B.2 C. 1或0 D. 0或1或2 8.设点(,)P x y 是曲线1(0,0)a x b y a b +=≥≥上任意一点,其坐标(,)x y 均满足2222212122x y x x y x +++++-+≤,则2a b +取值范围为( ▲ )A. (]0,2B. []1,2C. [)1,+∞D. [)2,+∞非选择题部分(共110分)二、 填空题 :本大题共7小题,第9,10每题三空,每空2分,第11,12题每题两空,每空3分,第13,14,15每空4分,共36分。
浙江省严州中学2015届高三仿真考试语文试题.doc

浙江省严州中学2015届高三仿真考试语文试题下列词语中,加点字的注音全都正确的一项是A.发酵(xiào)梵文(fàn)电饭煲(bāo)正当防卫(dàng) B.豆豉(chǐ)掺杂(cān)摆噱头(xué)叨陪鲤对(tāo) C.鸭肫(zhūn)毗邻(lín)腌笃鲜(dǔ)按捺不住(nài) D.苋菜(xiàn)绯闻(fēi)鸡血石(xuè)空穴来风(xué)【答案解析】D(A酵jiàoB掺chānC捺nà)2下列各句中,没有错别字的一项是A.王岳川先生认为,时间的重量往往凝聚在史诗的叙述中,它所启迪的不是一代人,而是无数代人的心智,并且成为他们的集体无意识。
B.羊年春节已过,回过头盘点春节关键词时,人们似乎发现这个春节多了很多现代元素,比如“抢红包”无可质疑地占据了关键词头把交椅。
C.《狼图腾》在中国上映后获得了票房口碑双丰收,在蒙古国上映的首日,电影票便告售磬,在意大利也非常火爆,仅次于好莱坞动画大片《疯狂外星人》以及《灰姑娘》。
D.李宗伟是典型的东方文化熏陶下的羽毛球高手,性格非常内裣、谦虚。
他反应灵活,防守出色,回球变幻莫测,突击的爆发力强,步伐快捷,打法稳中带攻。
【答案解析】A(B质疑—置疑;C磬—罄;D暴—爆)3下列各句中,加点的词语运用正确的一项是A.近期鉴于银行保险理财纠纷、投资公司跑路方面的话题越来越多,作为拥有基金从业资格的证券从业人员,我觉得有必要给大家讲解几种常见的理财方式。
B.《数学的故事》是一部写给非专业人士看的数学史,正是因为这一读者定位,这本书没有循规蹈矩地平铺直叙,而是将数学置于一个更大的社会与历史背景中去描述。
C.无论写哪种文体,高考作文都不可写得十分隐讳,否则,容易导致阅卷老师误判。
D.在这个竞争日趋激烈的知识经济时代,如果胸无点墨、身无长物,是很难在社会上立足的。
高三数学-2015届高三3月综合测试数学试题

2015届高三3月综合测试数学试题一、填空题:本大题共14个小题,每小题5分,共70分.1.设复数122i ,i z z m =-=+(m ∈R ,i 为虚数单位),若12z z ⋅为实数,则m 的值为 ▲ . 【答案】2 【解析】试题分析:12(2i )(i)=(2m+1)+(2-m)i z z m ⋅=-+为实数,所以20, 2.m m -== 考点:复数概念,复数运算2.已知集合{2}A a =+,{1,1,3}B =-,且A B ⊆,则实数a 的值是 ▲ . 【答案】1 【解析】试题分析:由题意得:2,21,32,23,1a a a a ===或,解得1a = 考点:集合包含关系3.某林场有树苗3000棵,其中松树苗400棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的棵数为 ▲ . 【答案】20 【解析】试题分析:松树苗的棵数为400150=203000⨯ 考点:分层抽样4.在ABC ∆的边AB 上随机取一点P , 记CAP ∆和CBP ∆的面积分别为1S 和2S ,则122S S >的概率是 ▲ . 【答案】13【解析】试题分析:当12=2S S 时,点P 为边AB 三等分点M (靠近B 点),所以122S S >的概率是13BM AB = 考点:几何概型概率5.已知双曲线22221x y a b-=的一条渐近线方程为20x y -=,则该双曲线的离心率为 ▲【解析】试题分析:双曲线22221x y a b -=的渐近线方程为22220x y by x a b a-==±,,所以2,,a b c e ===考点:双曲线的离心率,双曲线渐近线6.右图是一个算法流程图,则输出S 的值是 ▲ .【答案】25 【解析】试题分析:第一次循环: 1,3S n ==,第二次循环: 4,5S n ==,第三次循环: 9,7S n ==,第四次循环: 16,9S n ==,第五次循环: 25,1110S n ==>,结束循环,输出25S = 考点:循环结构流程图7.函数()lg(23)x x f x =-的定义域为 ▲ . 【答案】(,0)-∞ 【解析】试题分析:由题意得230,23,0x x x x x ->><,所以定义域为(,0)-∞ 考点:函数定义域8.1,则此三棱锥的体积为 ▲ . 【答案】16【解析】,体积为21136=考点:三棱锥的体积9.在△ABC 中,已知3AB =,o 120A =,且ABC ∆的面积为,则BC 边长为 ▲ . 【答案】7 【解析】1sin 153,52bc A bc c b =⨯⨯⇒=⇒==,由余弦定理得22212cos 25930()49,7.2a b c bc A a =+-=+-⨯-==考点:余弦定理,三角形面积10.已知函数()2f x x x =-,则不等式)(1)f x f ≤的解集为 ▲ . 【答案】[)1,-+∞ 【解析】试题分析:由题意得:()f x 在(,1)-∞上单调递增,在(1,2)上单调递减,在(2,)+∞上单调递增,且1)(1)1f f ==,所以)(1)11f x f x x -⇔-+⇔≥-≤,即解集为[)1,-+∞考点:利用函数性质解不等式11.已知函数()2sin(2)(0)4f x x ωωπ=->的最大值与最小正周期相同,则函数()f x 在[11]-,上的单调增区间为 ▲ .【答案】13[,]44-【解析】试题分析:由题意得:2222T ππωω==⇒=,所以22()242k x k k Z ππππππ-≤-≤+∈,即1322()44k x k k Z -≤≤+∈,又[11]x ∈-,,所以1344x -≤≤,即单调增区间为13[,]44- 考点:三角函数性质12.设等比数列{}n a 的前n 项和为n S ,若435a a a ,,成等差数列,且33k S =,163k S +=-,其中k *∈N ,则2k S +的值为 ▲ . 【答案】129【解析】试题分析:由题意得:23452=+21(),2a a a q q q q ⇒=+⇒==-舍,由33k S =,163k S +=-得112196192k k k k k a S S a a q ++++=-=-==,,所以263+192=129k S +=-考点:等比数列性质13.在平面四边形ABCD 中,已知3AB =,2DC =,点,E F 分别在边,AD BC 上,且3AD AE = ,3BC BF = .若向量AB 与DC 的夹角为60,则AB EF ⋅ 的值为 ▲ .【答案】7 【解析】试题分析:因为,EF EA AB BF EF ED DC CF =++=++ ,所以32EF AB DC =+,从而1293222733AB DC AB EF AB ⨯+⨯⨯+⋅=⋅== 考点:向量数量积14.在平面直角坐标系xOy 中,若动点(,)P a b 到两直线1l :y x =和2l :2y x =-+的距离之和为22a b +的最大值为 ▲ . 【答案】18 【解析】=|||2|4a b a b -++-=,其图像为一个正方形,四个顶点分别为(1,1),(1,3),(3,1),(3,3)A B C D ----, 而22a b +表示到原点距离的平方,所以22a b +的最大值为218OD = 考点:线性规划求最值二、解答题 (本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.) 15.(本小题满分14分)已知向量(cos ,sin )θθ=a ,(2,1)=-b . (1)若⊥a b ,求sin cos sin cos θθθθ-+的值;(2)若2-=a b ,(0,)2θπ∈,求sin()4θπ+的值.【答案】(1) 13【解析】试题分析:(1)先由向量垂直得到等量关系:sin 2cos θθ=,再代入式子化简即可:sin cos 2cos cos 1sin cos 2cos cos 3θθθθθθθθ--==++ (2)先由2-=a b得-ab 2=,化简得12cos sin 0θθ-+=,再根据平方关系22cos sin 1θθ+=解得3sin 54cos 5θθ⎧=⎪⎪⎨⎪=⎪⎩,所以34sin()cos )()455θθθπ+=+=+=试题解析:(2)由(cos 2,sin 1)θθ-=-+a b 可得,-ab 2=,即12cos sin 0θθ-+=, ① ………………………………………10分 又22cos sin 1θθ+=,且(0,)2θπ∈ ②,由① ②可解得,3sin 54cos 5θθ⎧=⎪⎪⎨⎪=⎪⎩,……12分所以34sin()cos )()455θθθπ+=+=+=. ……………………14分考点:向量垂直,同角三角函数关系16.(本小题满分14分)如图,在三棱锥P ABC -中,点,E F 分别是棱,PC AC 的中点.(1)求证:PA //平面BEF ;(2)若平面PAB ⊥平面ABC ,PB BC ⊥,求证:BC PA ⊥.【答案】(1) 详见解析(2)详见解析 【解析】试题分析:(1)证明线面平行,一般利用其判定定理,即从线线平行出发,利用中位线性质得到//PA EF ,再结合线面平行判定定理条件进行论证,(2)先将面面垂直条件转化为线面垂直,过点P 作PD AB ⊥,则PD ⊥平面ABC ,从而PD BC ⊥,又P B B C ⊥,从而BC ⊥平面PAB ,因此BC PA ⊥试题解析:(1)在PAC ∆中,E 、F 分别是PC 、AC 的中点,所以//PA EF , 又PA ⊄平面BEF ,EF ⊂平面BEF ,所以//PA 平面BEF .……………………………………6分 (2)在平面PAB 内过点P 作PD AB ⊥,垂足为D . 因为平面PAB ⊥平面ABC ,平面PAB 平面ABC AB =,PD ⊂平面PAB ,所以PD ⊥平面ABC ,………………8分又BC ⊂平面ABC ,所以PD BC ⊥,…………………………10分考点:线面平行判定定理,面面垂直性质定理17.(本小题满分14分)某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x 米,圆心角为θ(弧度).(1)求θ关于x 的函数关系式;(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为y ,求y 关于x 的函数关系式,并求出x 为何值时,y 取得最大值?【答案】(1) 10210xxθ+=+ (2) 1x = 【解析】试题分析:(1)将扇环面的两段弧长和直线段长分别用θ与x 表示后,利用其和为30列式,再解出θ即可;(2)将花坛的面积和装饰总费用分别用θ与x 表示,再利用第(1)问的结果消去x ,从而可得到y 关于x 函数,然后可利用导数或基本等式求其最小值,并确定y 取最小值时x 的值.试题解析:(1)设扇环的圆心角为 ,则()30102(10)x x θ=++-, 所以10210xxθ+=+,…………………………………4分 (2) 花坛的面积为2221(10)(5)(10)550,(010)2x x x x x x θ-=+-=-++<<.…………7分装饰总费用为()9108(10)17010x x x θ++-=+, ……………………9分 所以花坛的面积与装饰总费用的比22550550==1701010(17)x x x x y x x -++---++, …11分令17t x =+,则3913243()101010y t t =-+≤,当且仅当t=18时取等号,此时121,11x θ==.答:当1x =时,花坛的面积与装饰总费用的比最大.…………………14分 (注:对y 也可以通过求导,研究单调性求最值,同样给分) 考点:函数在实际问题中的应用,基本不等式的应用. 18.(本小题满分16分)已知ABC ∆的三个顶点(1,0)A -,(1,0)B ,(3,2)C ,其外接圆为H . (1)若直线l 过点C ,且被H 截得的弦长为2,求直线l 的方程;(2)对于线段BH 上的任意一点P ,若在以C 为圆心的圆上都存在不同的两点,M N ,使得点M 是线段PN 的中点,求C 的半径r 的取值范围.【答案】(1) 3x =或4360x y --=. (2) 【解析】试题分析:(1)求ABC ∆的外接圆方程可用待定系数法或利用两边垂直平分线的交点先求出圆心,再利用两点之间距离公式求出半径,求出圆的方程后再利用待定系数法求出直线的方程,此时要注意分直线斜率存在和不存在两种情况讨论;(2)可设出点,P N 的坐标,再把点M 的坐标用其表示,把点,M N 的坐标代入圆的方程,利用方程组恒有解去考察半径的取值范围,但要注意,,P N M 三点不能重合,即圆和线段BH 无公共点.试题解析:(1)线段AB 的垂直平分线方程为0x =,线段BC 的垂直平分线方程为30x y +-=,所以外接圆圆心(0,3)H,H 的方程为22(3)10x y +-=.………………4分设圆心H 到直线l 的距离为d ,因为直线l 被H 截得的弦长为2,所以3d =. 当直线l 垂直于x 轴时,显然符合题意,即3x =为所求;…………………………6分 当直线l 不垂直于x 轴时,设直线方程为2(3)y k x -=-3=,解得43k =, 综上,直线l 的方程为3x =或4360x y --=. ……………………………………8分 (2) 直线BH 的方程为330x y +-=,设(,)(01),(,)P m n m N x y ≤≤, 因为点M 是点P ,N 的中点,所以(,)22m x n yM ++,又,M N 都在半径为r 的C 上, 所以222222(3)(2),(3)(2).22x y r m x n y r ⎧-+-=⎪⎨++-+-=⎪⎩即222222(3)(2),(6)(4)4.x y r x m y n r ⎧-+-=⎪⎨+-++-=⎪⎩……………10分 因为该关于,x y 的方程组有解,即以(3,2)为圆心r 为半径的圆与以(6,4)m n --为圆心2r 为半径的圆有公共点,所以2222(2)(36)(24)(2)r r m n r r -≤-++-+≤+, …12分 又330m n +=-,所以2221012109r m m r +-≤≤对[01]m ∀∈,]成立. 而()2101210f m m m =+-在上的值域为[325,10],故2325r ≤且2r 10≤9. 15分又线段BH 与圆C 无公共点,所以222(3)(332)m m r -+-->对[01]m ∀∈,成立,即2325r <.故C 的半径r的取值范围为. ……………………………16分 考点:圆的方程,直线与圆的位置关系,圆与圆的位置关系.19.(本小题满分16分)已知函数325()2f x x x ax b =+++(,a b 为常数),其图象是曲线C .(1)当2a =-时,求函数()f x 的单调减区间;(2)设函数()f x 的导函数为()f x ',若存在唯一的实数0x ,使得00()f x x =与0()0f x ='同时成立,求实数b 的取值范围;(3)已知点A 为曲线C 上的动点,在点A 处作曲线C 的切线1l 与曲线C 交于另一点B ,在点B 处作曲线C 的切线2l ,设切线12,l l 的斜率分别为12,k k .问:是否存在常数λ,使得21k k λ=?若存在,求出λ的值;若不存在,请说明理由.【答案】 (1)1(2,)3-;(2)71(,)(,)548-∞--+∞ ;(3)当2512a =时,存在常数4λ=,使214k k =;当2512a ≠时,不存在常数λ,使21k k λ=. 【解析】(3) 设00(,())A x f x ,则点A 处切线方程为000()()()y f x f x x x '-=-,与曲线C :()y f x =联立方程组,得000()()()()f x f x f x x x '-=-,即2005()[(2)]02x x x x -++=,所以B 点的横坐标05(2)2B x x =-+. (12)分由题意知,21000()35k f x x x a '==++,22000525(2)122024k f x x x a '=--=+++,若存在常数λ,使得21k k λ=,则220000251220(35)4x x a x x a λ+++=++, 即常数λ,使得20025(4)(35)(1)4x x a λλ-+=--, 所以常数λ,使得40,25(1)0.4a λλ-=⎧⎪⎨--=⎪⎩解得常数λ,使得4λ=,2512a =. ………15分故当2512a =时,存在常数4λ=,使214k k =;当2512a ≠时,不存在常数λ,使21k k λ=.16分考点:函数与方程、导数的综合应用. 20.(本小题满分16分)已知数列{}n a 满足1a x =,23a x =,2*1132(2,)n n n S S S n n n +-++=+∈N ≥,n S 是数列{}n a 的前n 项和.(1)若数列{}n a 为等差数列. (ⅰ)求数列的通项n a ;(ⅱ)若数列{}n b 满足2n a n b =,数列{}n c 满足221n n n n c t b tb b ++=--,试比较数列{}n b 前n 项和n B 与{}n c 前n 项和n C 的大小;(2)若对任意*n ∈N ,1n n a a +<恒成立,求实数x 的取值范围. 【答案】(1)(ⅰ)21n a n =-;(ⅱ)详见解析;(2)137,156⎛⎫⎪⎝⎭.【解析】试题分析:(1)(ⅰ)由12,a a 可得12,S S ,在递推关系式2*1132(2,)n n n S S S n n n +-++=+∈N ≥中,由12,S S 可求3S ,进而求出3a ,于是可利用{}n a 是等差数列求出x 的值,最后可求出{}n a 的通项公式,(ⅱ)易知()21641n n C t t B =--,所以要比较n C 和n B 的大小,只需确定n B 的符号和21641t t --和1的大小关系问题,前者易知为正,后者作差后判断符号即可;(2)本题可由递推关系式21132n n n S S S n +-++=+通过变形得出36(2)n n a a n +-=≥,于是可以看出任意*n ∈N ,1n n a a +<恒成立,须且只需12345a a a a a <<<<,从而可以求出x 的取值范围. 试题解析:(1)(ⅰ)因为21132(2,*)n n n S S S n n n +-++=+∈N ≥,所以32114S S S ++=,即3212314a a a ++=,又12,3a x a x ==,所以3149a x =-, ……………………2分 又因为数列{}n a 成等差数列,所以2132a a a =+,即()6149x x x =+-,解得1x =, 所以()()()1111221*n a a n d n n n =+-=+-⨯=-∈N ; ……………………4分 (ⅱ)因为()21*n a n n =-∈N ,所以21220n a n n b -==>,其前n 项和0n B >,又因为()22211641n n n n n c t b tb b t t b ++=--=--, …………………………………5分 所以其前n 项和()21641n n C t t B =--,所以()22821n n n C B t t B -=--, ……7分当14t <-或12t >时,n n C B >;当14t =-或12t =时,n n C B =;当1142t -<<时,n n C B <.…………………………………………………………9分(2)由21132(2,*)n n n S S S n n n +-++=+∈N ≥知()221312(*)n n n S S S n n ++++=++∈N ,两式作差,得2163(2,*)n n n a a a n n n ++++=+∈N ≥, ……………………10分 所以()321613(*)n n n a a a n n +++++=++∈N ,再作差得36(2,*)n n a a n n +-=∈N ≥,………………………………………………11分 所以,当1n =时,.1n a a x ==;当31n k =-时,().31216366234n k a a a k x k n x -==+-⨯=+-=+-; 当3n k =时,().331614966298n k a a a k x k n x ==+-⨯=-+-=-+;当31n k =+时,().314161666267n k a a a k x k n x +==+-⨯=++-=+-;……14分 因为对任意*n ∈N ,1n n a a +<恒成立,所以12a a <且3133132k k k k a a a a -++<<<, 所以363669869866566563x xk x k x k x k x k x k x<⎧⎪+-<-+⎪⎨-+<+-⎪⎪+-<+⎩,解得,137156x <<,故实数x 的取值范围为137,156⎛⎫⎪⎝⎭.…………………………………………………16分考点:等差数列、等比数列与函数、不等式的综合运用.附加题21.B (选修4—2:矩阵与变换)(本小题满分10分)设矩阵00a b ⎡⎤=⎢⎥⎣⎦M (其中00a b >,>),若曲线C :221x y +=在矩阵M 所对应的变换作用下得到曲线2214x C y '+=:,求a b +的值.【答案】3.【解析】试题分析:本题可先求出曲线C 在矩阵M 所对应的变换作用下得到曲线C '的方程再与方程2214x y +=加以比较得出a b ,的值,也可在曲线C 上取两特殊点经阵M 所对应的变换作用下得到点在曲线C '上,代入C '方程,求出a b ,的值. 试题解析:设曲线C :221x y +=上任意一点(,)P x y ,在矩阵M 所对应的变换作用下得到点111(,)P x y ,则1100x a x b y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即11ax x by y =⎧⎨=⎩. …………………………………………………………5分又点111(,)P x y 在曲线2214x C y '+=:上,所以221114x y +=,则2214ax by +=为曲线C 的方程. 又曲线C 的方程为221x y +=,故24a =,21b =,因为00a b >,>,所以3a b +=. …………………………………………………………10分考点:矩阵与变换.21.C (选修4—4:坐标系与参数方程)(本小题满分10分)在平面直角坐标系xOy 中,已知直线l的参数方程是x y ⎧⎪⎪⎨⎪+⎪⎩,(t 为参数);以O 为极点,x 轴正半轴为极轴的极坐标系中,圆C 的极坐标方程为2cos()4ρθπ=+.由直线l 上的点向圆C 引切线,求切线长的最小值. 【答案】62. 【解析】试题分析:先将圆C 的极坐标方程化为直角坐标方程,再把直线上的点的坐标(含参数)代入,化为求函数的最值问题,也可将直线l 的参数方程化为普通方程,根据勾股定理转化为求圆心到直线上最小值的问题试题解析:因为圆C 的极坐标方程为θθρsin 2cos 2-=,所以θρθρρsin 2cos 22-=,所以圆C 的直角坐标方程为02222=+-+y x y x ,圆心为⎪⎪⎭⎫⎝⎛-22,22,半径为1,…4分因为直线l的参数方程为,x y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数), 所以直线l上的点P +⎝向圆C 引切线长是所以直线l 上的点向圆C 引的切线长的最小值是62. ……………………………………10分考点:直线的参数方程和圆的极坐标方程,圆的切线长. 22.(本小题满分10分)某品牌汽车4S 店经销,,A B C 三种排量的汽车,其中,,A B C 三种排量的汽车依次有5,4,3款不同车型.某单位计划购买3辆不同车型的汽车,且购买每款车型等可能. (1)求该单位购买的3辆汽车均为B 种排量汽车的概率;(2)记该单位购买的3辆汽车的排量种数为X ,求X 的分布列及数学期望. 【答案】(1)155;(2)详见解析. 【解析】试题分析:(1)这是一个古典概型问题,先求出从15款车型中任买3辆共有多少种可能,再求出购买3辆车都为B 种车有多少种可能,即可求出结果;(2)X 的所有可能取值为1,2,3,对每种情况要准确分类,求出各种情况下有多少种可能,就可求出X 各种取值的概率,然后再求数学期望.试题解析:(1)设该单位购买的3辆汽车均为B 种排量汽车为事件M ,则343121().55C P M C ==所以该单位购买的3辆汽车均为B 种排量汽车的概率为155. ………………………………4分 (2)随机变量X 的所有可能取值为1,2,3.则3335433123(1),44C C C P X C ++===1115433123(3)11C C C P X C ===, 29(2)1(1)(3)44P X P X P X ==-=-==. 所以X 的分布列为……………………………8分数学期望329397()12344441144E X =⨯+⨯+⨯=.………………………………………………10分 考点:随机变量的概率分布. 23.(本小题满分10分)已知点(1,0)A -,(1,0)F ,动点P 满足2||AP AF FP ⋅=. (1)求动点P 的轨迹C 的方程;(2)在直线l :22y x =+上取一点Q ,过点Q 作轨迹C 的两条切线,切点分别为,M N .问:是否存在点Q ,使得直线MN //l ?若存在,求出点Q 的坐标;若不存在,请说明理由.【答案】(1)24y x =;(2)1(,1)2Q -.考点:曲线与方程.。
浙江省杭州市严州中学届高三数学下学期3月段考试卷文(含解析)【含答案】

浙江省杭州市严州中学2015届高三下学期3月段考数学试卷(文科)一、选择题:本大题共8小题,每小题5分,共40分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U=R,集合A={x|x≥2},B={x|0≤x<5},则集合(∁U A)∩B=()A.{x|0<x<2} B.{x|0≤x<2} C.{x|0<x≤2}D.{x|0≤x≤2}2.已知等差数列{a n}满足:a3=13,a13=33,则数列{a n}的公差为()A.1 B.2 C.3 D.43.若0<x<,则xtanx<1是xsinx<1的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.设<<<1,那么()A.a a<a b<b a B.a a<b a<a b C.a b<a a<b a D.a b<b a<a a5.已知α、β为锐角,,,则tanβ=()A.B.3 C.D.6.已知平面向量=(1,),|﹣|=1.则||的取值范围是()A.[0,1] B.[1,3] C.[2,4] D.[3,4]7.已知定义在R上的奇函数f(x)=的图象如图所示,则a,b,c的大小关系是()A.a>b>c B.c>a>b C.b>a>c D.a>c>b8.如图,已知双曲线C:﹣=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P、Q,若∠PAQ=60°且=3,则双曲线C的离心率为()A.B.C.D.二、填空题:本大题共7小题,前4小题每题6分,后3小题每题4分,共36分.9.函数f(x)=log2(4﹣x2)的定义域为,值域为,不等式f(x)>1的解集为.10.一个简单几何体的三视图如图所示,其中正视图是一个正三角形,俯视图是等腰直角三角形,则该几何体的体积为,表面积为.11.如果实数x,y满足:,则的取值范围是,z=+的最大值为.12.已知数列{a n}满足:a1=2,(n+1)a n=(n﹣1)a n﹣1(n≥2,n∈N*),则=,数列{a n}的通项公式为.13.已知点A(2,0),B(﹣2,4),C(5,8),若线段AB和CD有相同的中垂线,则点D 的坐标是.14.在△ABC中,角A,B,C所对的边分别为a,b,c,CD是AB边上的高,且a2+c2<b2,sin2A+sin2B=1,则sin(A﹣B)=.15.如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,点E,F为PA,PD的中点,则面BCFE将四棱锥P﹣ABCD所分成的上下两部分的体积的比值为.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.在△ABC中,角A,B,C所对的边分别是a,b,c,且满足:a2=(b﹣c)2+(2﹣)bc,又sinAsinB=.(Ⅰ)求角A的大小;(Ⅱ)若a=2,求△ABC的面积S.17.如图所示,四棱锥P﹣ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.(Ⅰ)求证:直线EA⊥平面PAB;(Ⅱ)求直线AE与平面PCD所成角的正切值.18.已知各项均为正数的数列{a n}的前n项和为S n,且2S n=4a n﹣1.在数列{b n}中,b n+1=b n﹣2,b4+b8=﹣16.(Ⅰ)求a n,b n;(Ⅱ)设c n=求数列{c n}的前项和T n.19.已知抛物线Γ:y2=2px,准线与x轴的交点为P(﹣2,0).(Ⅰ)求抛物线Γ的方程;(Ⅱ)如图,Q(1,0),过点P的直线l与抛物线Γ交于不同的两点A,B,AQ与BQ分别与抛物线Γ交于点C,D,设AB,DC的斜率分别为k1,k2,AD,BC的斜率分别为k3,k4,问:是否存在常数λ,使得k1k3k4=λk2,若存在,求出λ的值,若不存在,说明理由.20.已知函数f(x)=ax2+bx﹣(a>0),g(x)=4x++,且y=f(x+)为偶函数.设集合A={x|t﹣1≤x≤t+1}.(Ⅰ)若t=﹣,记f(x)在A上的最大值与最小值分别为M,N,求M﹣N;(Ⅱ)若对任意的实数t,总存在x1,x2∈A,使得|f(x1)﹣f(x2)|≥g(x)对∀x∈[0,1]恒成立,试求a的最小值.浙江省杭州市严州中学2015届高三下学期3月段考数学试卷(文科)一、选择题:本大题共8小题,每小题5分,共40分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U=R,集合A={x|x≥2},B={x|0≤x<5},则集合(∁U A)∩B=()A.{x|0<x<2} B.{x|0≤x<2} C.{x|0<x≤2}D.{x|0≤x≤2}考点:交、并、补集的混合运算.专题:计算题.分析:根据全集U=R,集合A={x|x≥2},易知C U A={x|x<2}再根据交集定义即可求解解答:解:∵全集U=R,集合A={x|x≥2}∴C U A={x|x<2}∵B={x|0≤x<5}∴(C U A)∩B={x|0≤x<2}故选B点评:本题考查了补集、交集及其运算,属于基础题.2.已知等差数列{a n}满足:a3=13,a13=33,则数列{a n}的公差为()A.1 B.2 C.3 D.4考点:等差数列的通项公式.专题:等差数列与等比数列.分析:利用d=计算即得结论.解答:解:依题意,公差d===2,故选:B.点评:本题考查等差数列的简单性质,注意解题方法的积累,属于基础题.3.若0<x<,则xtanx<1是xsinx<1的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据充分条件和必要条件的定义进行判断即可.解答:解:∵0<x<,分别画出y=xtanx(红色曲线),和y=xsinx(绿色曲线),如图所示,由图象可知,∴tanx>sinx>0,∴xtanx<1⇒xsinx<1,反之不成立,因此xtanx<1是xsinx<1的充分不必要条件.故选:A.点评:本题考查了三角函数的单调性、简易逻辑的判定,属于基础题4.设<<<1,那么()A.a a<a b<b a B.a a<b a<a b C.a b<a a<b a D.a b<b a<a a考点:指数函数单调性的应用.专题:计算题.分析:先由条件结合指数函数的单调性,得到0<a<b<1,再由问题抽象出指数函数和幂函数利用其单调性求解.解答:解:∵<<<1且y=()x在R上是减函数.∴0<a<b<1∴指数函数y=a x在R上是减函数∴a b<a a∴幂函数y=x a在R上是增函数∴a a<b a∴a b<a a<b a故选C.点评:本题主要考查指数函数、幂函数的图象及其单调性.5.已知α、β为锐角,,,则tanβ=()A.B.3 C.D.考点:两角和与差的正切函数;同角三角函数间的基本关系.专题:计算题;三角函数的求值.分析:依题意,可求得tanα=,再利用两角差的正切即可求得tanβ的值.解答:解:∵α锐角,cosα=,∴sinα=,∴tanα==,又tan(α﹣β)=﹣,β为锐角,∴tanβ=tan[α﹣(α﹣β)]===3,故选:B.点评:本题考查两角差的正切,考查同角三角函数间的基本关系,属于中档题.6.已知平面向量=(1,),|﹣|=1.则||的取值范围是()A.[0,1] B.[1,3] C.[2,4] D.[3,4]考点:平面向量数量积的坐标表示、模、夹角.专题:平面向量及应用.分析:由模长公式和圆的知识,可把问题转化为点(x,y)与原点的距离的取值范围,由距离公式和圆的知识易得答案.解答:解:设=(x,y),则由题意可得﹣=(1﹣x,﹣y),由|﹣|=1可得(x﹣1)2+(y﹣)2=1,即点(x,y)在以(1,)为圆心1为半径的圆上,而||=表示点(x,y)与原点的距离,又圆心(1,)与原点的距离d=2,∴最小值为2﹣1=1,最大值为2+1=3故选:B点评:本题考查平面向量的数量积,涉及圆的知识及数形结合思想,属中档题.7.已知定义在R上的奇函数f(x)=的图象如图所示,则a,b,c的大小关系是()A.a>b>c B.c>a>b C.b>a>c D.a>c>b考点:函数的图象;函数奇偶性的性质.专题:函数的性质及应用.分析:根据函数的定义域为R,得到c>0,根据函数过原点得到b=0,根据f(1)=1,判断a,c的关系.解答:解:∵函数过原点,∴f(0)==0,∴b=0,由图象知函数的定义域为R,则c>0,又f(1)=1,即f(1)=,则a=1+c>c,∴a>c>b,故选:D点评:本题主要考查函数图象的识别和应用,根据函数图象的特点转化为函数的性质是解决本题的关键.8.如图,已知双曲线C :﹣=1(a >0,b >0)的右顶点为A ,O 为坐标原点,以A 为圆心的圆与双曲线C 的某渐近线交于两点P 、Q ,若∠PAQ=60°且=3,则双曲线C 的离心率为()A .B .C .D .考点: 双曲线的简单性质.专题: 计算题;圆锥曲线的定义、性质与方程.分析: 确定△QAP 为等边三角形,设AQ=2R ,则OP=R ,利用勾股定理,结合余弦定理,即可得出结论.解答: 解:因为∠PAQ=60°且=3,所以△QAP 为等边三角形, 设AQ=2R ,则OP=R ,渐近线方程为y=x ,A (a ,0),取PQ 的中点M ,则AM=由勾股定理可得(2R )2﹣R 2=()2,所以(ab )2=3R 2(a 2+b 2)① 在△OQA 中,=,所以7R 2=a 2②①②结合c 2=a 2+b 2,可得=.故选:B .点评: 本题考查双曲线的性质,考查余弦定理、勾股定理,考查学生的计算能力,属于中档题.二、填空题:本大题共7小题,前4小题每题6分,后3小题每题4分,共36分.9.函数f(x)=log2(4﹣x2)的定义域为(﹣2,2),值域为(﹣∞,2],不等式f(x)>1的解集为.考点:对数函数的图像与性质.专题:计算题.分析:先利用对数的真数大于0求该函数的定义域,根据函数图象来求其值域;根据题意列出不等式,通过解不等式求f(x)>1的解集.解答:解:依题意得:4﹣x2>0,解得﹣2<x<2,所以该函数的定义域为:(﹣2,2).∵4﹣x2>0,∴(4﹣x2)最大值=4,∴在(﹣2,2)上,该函数的值域为:(﹣∞,2].由f(x)>1得到:log2(4﹣x2)>1,则4﹣x2>2,解得﹣<x<.故不等式f(x)>1的解集为.故答案是:(﹣2,2);(﹣∞,2];.点评:本题考查了对数函数定义域的求法,考查了对数函数的值域,是基础的计算题.10.一个简单几何体的三视图如图所示,其中正视图是一个正三角形,俯视图是等腰直角三角形,则该几何体的体积为,表面积为.考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,求出底面面积,代入棱锥体积公式,可得几何体的体积,累加各个面的面积可得,几何体的表面积.解答:解:由三视图知:几何体是三棱锥,且几何体的后侧面SAC与底面垂直,高SO为,如图:其中OA=OB=OC=1,SO⊥平面ABC,AB=BC=,SA=SB=SC=2,底面△ABC的面积为:,后侧面△SAC的面积为:,左右两个侧面△SAB和△SBC的底面边长为,两腰长为2,故底边上的高为:=,故左右两个侧面△SAB和△SBC的面积为:,故几何体的表面积:,几何体的体积V==,故答案为:,点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.11.如果实数x,y满足:,则的取值范围是[,2],z=+的最大值为.考点:简单线性规划.专题:不等式的解法及应用.分析:根据已知的约束条,画出满足约束条件的可行域,将式子进行变形,再分析目标函数的几何意义,结合图象即可给出目标函数的取值范围.解答:解:约束条件对应的平面区域如下图示:设k=,则z表示可行域内的点(x,y)与点(0,0)连线的斜率,由图可知z的最大值为直线2x﹣y=0的斜率2,最小值为直线OC的斜率,由,得,即C(3,1),则OC的斜率k=,故k=的取值范围是[,2],又z=+=k+在[,1]上单调递减,在[1,2]上递增,则当t=1时,z=1+1=2,当t=时,z=+3=,∵>2,∴z=+=k+在[,2]上的最大值为,故答案为:[],点评:本题主要考查线性规划的应用,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.12.已知数列{a n}满足:a1=2,(n+1)a n=(n﹣1)a n﹣1(n≥2,n∈N*),则=,数列{a n}的通项公式为.考点:数列递推式.专题:等差数列与等比数列.分析:通过对(n+1)a n=(n﹣1)a n﹣1(n≥2,n∈N*)变形可知=(n≥2,n∈N*),累乘计算即得结论.解答:解:∵(n+1)a n=(n﹣1)a n﹣1(n≥2,n∈N*),∴=(n≥2,n∈N*),∵=,=,∴=•=,同时累乘得:=••…•=,又∵a1=2,∴a n=•2=,故答案为:、.点评:本题考查数列的通项,注意解题方法的积累,属于中档题.13.已知点A(2,0),B(﹣2,4),C(5,8),若线段AB和CD有相同的中垂线,则点D 的坐标是(﹣6,7).考点:直线的一般式方程与直线的垂直关系.专题:直线与圆.分析:设D(x,y),由题意可得CD的中点在AB的垂直平分线且CD∥AB,可得x和y的方程组,解方程组可得.解答:解:设D(x,y),∵A(2,0),B(﹣2,4),∴AB点E(0,2),AB的斜率k==﹣1,∴AB的垂直平分线的斜率为1,∴AB的垂直平分线的方程为y=x+2,∴CD的中点F(,)在y=x+2上,∴﹣+2=0,①又CD的斜率=﹣1,②联立①②解得,即D(﹣6,7),故答案为:(﹣6,7).点评:本题考查线段的中点公式、两条直线垂直的性质,用点斜式求直线的方程,属基础题.14.在△ABC中,角A,B,C所对的边分别为a,b,c,CD是AB边上的高,且a2+c2<b2,sin2A+sin2B=1,则sin(A﹣B)=﹣1.考点:余弦定理.专题:三角函数的求值;解三角形.分析:根据余弦定理可得B是钝角,A和C是锐角,由:sin2A+sin2B=1,且sin2A+cos2A=1,可得cosA=sinB>0,sinA=﹣cosB>0,利用两角差的正弦函数公式即可得解.解答:解:根据余弦定理:cosB=<0,所以:B是钝角,△ABC是钝角三角形,所以:A和C是锐角,因为:sin2A+sin2B=1,因为:sin2A+cos2A=1,所以:cosA=sinB>0,所以:sinA=﹣cosB>0,所以:sin(A﹣B)=sinAcosB﹣cosAsinB=﹣cos2B﹣sin2B=﹣1.故答案为:﹣1.点评:本题主要考查了余弦定理,同角三角函数关系式,两角差的正弦函数公式的应用,属于基本知识的考查.15.如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,点E,F为PA,PD的中点,则面BCFE将四棱锥P﹣ABCD所分成的上下两部分的体积的比值为.考点:棱柱、棱锥、棱台的体积.专题:综合题;空间位置关系与距离.分析:不妨设ABCD是正方形,PD⊥平面ABCD,AD=2a,求出上下两部分的体积,即可得出结论.解答:解:不妨设ABCD是正方形,PD⊥平面ABCD,AD=2a,则V P﹣ABCD==a3,连接FA,FB,则V EFABCD=+=a3,∴V P﹣EFBC=a3,∴四棱锥P﹣ABCD所分成的上下两部分的体积的比值为.故答案为:.点评:本题考查体积的计算,考查学生的计算能力,正确计算体积是关键.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.在△ABC中,角A,B,C所对的边分别是a,b,c,且满足:a2=(b﹣c)2+(2﹣)bc,又sinAsinB=.(Ⅰ)求角A的大小;(Ⅱ)若a=2,求△ABC的面积S.考点:余弦定理;正弦定理.专题:解三角形.分析:(1)由已知整理可得,利用余弦定理可求cosA,即可解得A的值.(2)利用三角函数恒等变换的应用化简已知可得cos(A﹣B)=1,可得A,B,C的值,利用三角形面积公式即可得解.解答:解:(1)∵,∴,又∵,∴.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2)∵,∴2sinAsinB=1+cosC=1﹣cos(A+B),∴cosAcosB+sinAsinB=1即cos(A﹣B)=1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∴,,又∵,∴.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣点评:本题主要考查了三角函数恒等变换的应用,余弦定理,三角形面积公式的应用,属于基本知识的考查.17.如图所示,四棱锥P﹣ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.(Ⅰ)求证:直线EA⊥平面PAB;(Ⅱ)求直线AE与平面PCD所成角的正切值.考点:直线与平面所成的角;直线与平面垂直的判定.专题:证明题;立体几何.分析:(1)只需证明直线EA⊥AB,且EA⊥PA即可;(2)先证明AH⊥平面PCD,得出∠AEP为直线AE与平面PCD所成角,在Rt△PAE中计算tan∠AEP的值.解答:解:(1)证明:∵∠ADE=∠ABC=60°,ED=1,AD=2,∴△AED是以∠AED为直角的Rt△;又∵AB∥CD,∴EA⊥AB;又PA⊥平面ABCD,∴EA⊥PA;且AB∩PA=A,∴EA⊥平面PAB;﹣﹣﹣﹣﹣﹣﹣﹣﹣(2)如图所示,连结PE,过A点作AH⊥PE于H点,∵CD⊥EA,CD⊥PA,且PA∩EA=A,∴CD⊥平面PAE;又AH⊂平面PAE,∴AH⊥CD;又AH⊥PE,且CD∩AE=E,∴AH⊥平面PCD,∴∠AEP为直线AE与平面PCD所成角;﹣﹣﹣﹣﹣﹣在Rt△PAE中,∵PA=2,AE==,∴tan∠AEP===.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣点评:本题考查了空间中的垂直关系的应用问题,也考查了空间想象能力与逻辑思维能力,是基础题目.18.已知各项均为正数的数列{a n}的前n项和为S n,且2S n=4a n﹣1.在数列{b n}中,b n+1=b n ﹣2,b4+b8=﹣16.(Ⅰ)求a n,b n;(Ⅱ)设c n=求数列{c n}的前项和T n.考点:数列的求和;数列递推式.专题:等差数列与等比数列.分析:(Ⅰ)通过2S n=4a n﹣1可知2a n=S n+,易知,当n≥2时利用a n=S n﹣S n﹣1可知=2,进而可得数列{a n}的通项公式,利用b4+b8=2b6计算可得数列{b n}的通项公式;(Ⅱ)通过a n=2n﹣2、b n=4﹣2n可知c n=,利用错位相减法计算即得结论.解答:解:(Ⅰ)∵2S n=4a n﹣1,∴2a n=S n+,当n=1时,;当n≥2时,a n=S n﹣S n﹣1=2a n﹣2a n﹣1,整理得:=2,∴数列{a n}是以为首项,2为公比的等比数列,∴a n=a1•q n﹣1==2n﹣2;∵b n+1=b n﹣2,∴d=b n+1﹣b n=﹣2,又∵b4+b8=2b6=﹣16,∴b6=﹣8,∴b1=b6﹣5d=﹣8﹣5•(﹣2)=2,∴b n=b1+(n﹣1)d=2﹣2(n﹣1)=4﹣2n;(Ⅱ)∵a n=2n﹣2,b n=4﹣2n,∴c n===,∴T n=8•+0•+(﹣8)•+…+(24﹣8n)•+(16﹣8n)•,T n=8•+0•+…+(24﹣8n)•+(16﹣8n)•,两式相减得:T n=4﹣8(++…+)﹣(16﹣8n)•=4﹣8•﹣(16﹣8n)•=4﹣4(1﹣)﹣=,∴T n=.点评:本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.19.已知抛物线Γ:y2=2px,准线与x轴的交点为P(﹣2,0).(Ⅰ)求抛物线Γ的方程;(Ⅱ)如图,Q(1,0),过点P的直线l与抛物线Γ交于不同的两点A,B,AQ与BQ分别与抛物线Γ交于点C,D,设AB,DC的斜率分别为k1,k2,AD,BC的斜率分别为k3,k4,问:是否存在常数λ,使得k1k3k4=λk2,若存在,求出λ的值,若不存在,说明理由.考点:抛物线的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(Ⅰ)利用抛物线的性质,求出p,即可求抛物线Γ的方程;(Ⅱ)假设存在实数λ,设AB的直线方程为x=my﹣2,与抛物线方程联立,由化简可得y1y3=﹣8,同理可得y2y4=﹣8,利用k1k3k4=λk2,求出λ的值.解答:解:(Ⅰ)因为准线与x轴的交点为P(﹣2,0),所以p=4.所以抛物线Γ的方程为y2=8x﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(Ⅱ)假设存在实数λ设AB的直线方程为x=my﹣2,,,,由化简得:y2﹣8my+16=0所以﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣由化简可得y1y3=﹣8,同理可得y2y4=﹣8﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣因为,,,所以代入k1k3k4=λk2得y1y2=,所以存在λ=﹣8﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.20.已知函数f(x)=ax2+bx﹣(a>0),g(x)=4x++,且y=f(x+)为偶函数.设集合A={x|t﹣1≤x≤t+1}.(Ⅰ)若t=﹣,记f(x)在A上的最大值与最小值分别为M,N,求M﹣N;(Ⅱ)若对任意的实数t,总存在x1,x2∈A,使得|f(x1)﹣f(x2)|≥g(x)对∀x∈[0,1]恒成立,试求a的最小值.考点:函数恒成立问题;二次函数的性质.专题:函数的性质及应用;不等式的解法及应用.分析:(Ⅰ)由偶函数的定义,可得b=﹣,将f(x)配方,由对称轴和区间的关系,可得最大值和最小值,可得M﹣N=a;(Ⅱ)设2x=t,求得g(x)的解析式(用t表示),求出最大值,结合条件可得a≥,证明在[t﹣1,t+1]上总存在两点x1、x2,使得成立.注意运用二次函数的单调性,即可得到a的最小值.解答:解:(Ⅰ)=为偶函数,所以;即t=,f(x)=ax2﹣x﹣=a(x﹣)2﹣﹣,在区间上,∵,∴M﹣N=a;(Ⅱ)设2x=t,∵x∈[0,1],∴t=2x∈[1,2],,所以g(x)的最大值为.依题意原命题等价于在A上,总存在两个点.即只需满足在A上.因为对任意的t都成立,所以当也成立,由(1)知,,下面证明在[t﹣1,t+1]上总存在两点x1、x2,使得成立.当t≥1时,f(x)在[t,t+]递增,当t<1时,f(x)在[t﹣1,t]递减,则|f(x1)﹣f(x2)|max≥f(t+1)﹣f(t)=t﹣≥,|f(x1)﹣f(x2)|max≥f(t﹣1)﹣f(t)=﹣t>,综上所述,.点评:本题考查函数的奇偶性和单调性的判断及运用,同时考查不等式的恒成立问题的解法,考查运算能力,属于中档题.。
浙江省建德市严州中学2015届高三文综测试卷(二) Word版含答案
严州中学2015届高三文综测试卷(二)第Ⅰ卷选择题(共140分)选择题部分共35小题,每小题4分,共140分。
在每题给出的四个选项中,只有一项是符合题目要求的。
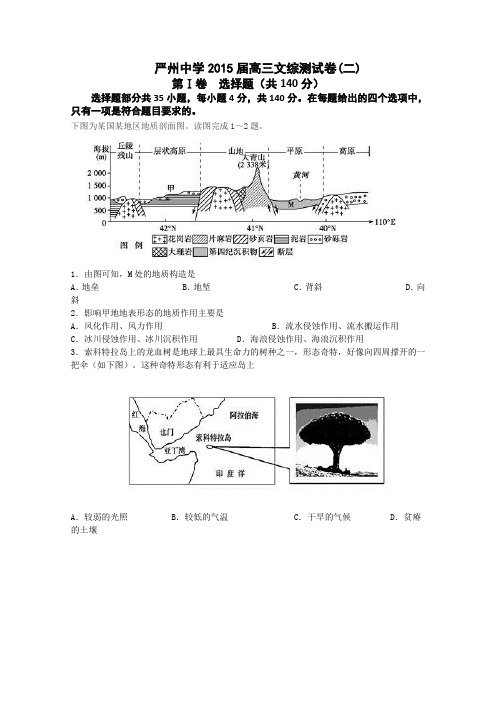
下图为某国某地区地质剖面图。
读图完成1~2题。
1.由图可知,M处的地质构造是A.地垒 B.地堑 C.背斜 D.向斜2.影响甲地地表形态的地质作用主要是A.风化作用、风力作用 B.流水侵蚀作用、流水搬运作用C.冰川侵蚀作用、冰川沉积作用 D.海浪侵蚀作用、海浪沉积作用3.索科特拉岛上的龙血树是地球上最具生命力的树种之一,形态奇特,好像向四周撑开的一把伞(如下图)。
这种奇特形态有利于适应岛上A.较弱的光照 B.较低的气温 C.干旱的气候 D.贫瘠的土壤4.下图为南苏丹共和国位置图和南苏丹水系图。
造成南苏丹境内沼泽广布的原因有A.终年多雨,上游来水充足,洪水泛滥B.盆地地形,河网密布,排水不畅C.地势高,地下分布多年冻土,不利于地表水下渗D.气温低,蒸发弱,地表积水多下图是某国人口年龄结构图。
读图完成5~6题。
5.各年龄段中,外来移民占本国总人口的比重最高的是A.20岁以下 B.20~50岁C.50~65岁 D.65岁以上6.该国人口增长模式是A.原始型 B.传统型 C.过渡型 D.现代型下图是我国某类企业分布示意图。
根据相关知识,读图完成7~8题。
7.该企业部门可能是A.纺织工业 B.石油化工 C.制糖工业 D.冶金工业8.近年来,该工业呈现出由内陆地区向东部沿海城市布局的演化态势,其主要因素是A.原料 B.市场 C.交通 D.技术下图为世界某区域,读图,完成9~10题。
9.图示区域的自然景观A.以东西方向变化为主B.以南北方向变化为主C.以热带荒漠植被为主D.以亚热带常绿林为主10.图中陆地东部地区自然带对应的气候类型是A.热带草原气候B.热带沙漠气候C.热带雨林气候D.热带季风气候图5虚线是地球公转到近日点附近的晨昏线,甲点以东为西半球,甲点与乙、丙两点间的最短距离是3330Km。
数学(文)卷·2015届浙江省严州中学高三仿真考试(二)(2015.05)

2015年普通高等学校招生全国统一考试(浙江卷)文科数学仿时卷本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页,非选择题部分2至4页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共40分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
参考公式:球的表面积公式 棱柱的体积公式24S R π= V Sh=球的体积公式 其中S 表示棱柱的底面积,h 表示棱柱的高334R V π=棱台的体积公式其中R 表示球的半径)(312211S S S S h V ++=棱锥的体积公式 其中S 1、S 2分别表示棱台的上、下底面积,13V Sh= h 表示棱台的高其中S 表示棱锥的底面积,h 表示棱锥的高一.选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设a ∈R ,则“a=-32”是“直线l 1: ax+2y -1=0与直线l 2: x+a(a+1)y+4=0垂直”的( )A. 充分必要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件2.设m ,n 是两条不同的直线,α,β是两个不同的平面,下列命题正确的是 ( )A. m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βB. m ∥α,n ∥β,且α∥β,则m ∥nC. m ⊥α, n ⊂β, m ⊥n ,则α⊥βD. m ⊥α,n ⊥β,且α⊥β,则m ⊥n3.设函数2211()21x x f x x x x ⎧-⎪=⎨+->⎪⎩,,,, ≤则1(2)f f ⎛⎫⎪⎝⎭的值为( ) A .2716-B .1516C .89 D .184.()sin()(0,)2f x x πωϕωϕ=+><的最小正周期是π,若其图象向左平移6π个单位后得到的函数为奇函数,则函数()f x 的图象 ( )A.关于点(,0)12π对称 B.关于点5(,0)12π对称C.关于直线512x π=对称 D.关于直线12x π=对称5.设实数列{a n }和{b n }分别为等差数列与等比数列,且a 1=b 1=8,a 4=b 4=1,则以下结论正确的是 ( )A . a 2>b 2B . a 3<b 3C . a 5>b 5D . a 6>b 66.设4,a b ⋅=r r 若a r 在b r 方向上的投影为2,且b r 在a r 方向上的投影为1,则a r 与b r 的夹角等于 ( )A .6πB .3πC .23πD .3π或23π7.如图,正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,P 为BC 的中点,Q 为线段CC 1上的动点,过点A ,P ,Q 的平面截该正方体所得的截面记为S ,则下列结论错误的是 ( )A 、当0<CQ <时,S 为四边形B 、截面在底面上投影面积恒为定值C 、存在某个位置,使得截面S 与平面A 1BD 垂直D 、当CQ=34时,S 与C 1D 1的交点R 满足C 1R=8.在等腰梯形ABCD 中,//,2,1,2AB CD AB AD CD x===且 其中(0,1)x ∈,以,A B 为焦点且过点D 的双曲线的离心率为1e ,以,C D 为焦点且过点A 的椭圆的离心率为2e ,若对任意(0,1)x ∈不等式12t e e <+恒成立,则t 的最大值为( )A.B.C. 2D.第II 卷(非选择题,共l10分)二、填空题:本大题共7小题,第9-12题每题6分,第13-15题每题4分,共36分。
浙江省严州中学2015届高三仿真考试语文试卷.pdf

严州中学2015届高三仿真考试语文试卷 一、语言文字运用(共24分,其中选择题每小题3分) 1.下列词语中,加点字的注音全都正确的一项是 A.发酵(xiào) 梵文(fàn) 电饭煲(bāo) 正当防卫(dàng) B.豆豉(chǐ) 掺杂(cān) 摆噱头(xué) 叨陪鲤对(tāo) C.鸭肫 (zhūn) 毗邻(lín) 腌笃鲜(dǔ) 按捺不住(nài) D.苋菜(xiàn) 绯闻 (fēi) 鸡血石(xuè) 空穴来风(xué) 2.下列各句中,没有错别字的一项是 A.王岳川先生认为,时间的重量往往凝聚在史诗的叙述中,它所启迪的不是一代人,而是无数代人的心智,并且成为他们的集体无意识。
B.羊年春节已过,回过头盘点春节关键词时,人们似乎发现这个春节多了很多现代元素,比如“抢红包”无可质疑地占据了关键词头把交椅。
C.《狼图腾》在中国上映后获得了票房口碑双丰收,在蒙古国上映的首日,电影票便告售磬,在意大利也非常火爆,仅次于好莱坞动画大片《疯狂外星人》以及《灰姑娘》。
D.李宗伟是典型的东方文化熏陶下的羽毛球高手,性格非常内裣、谦虚。
他反应灵活,防守出色,回球变幻莫测,突击的爆发力强,步伐快捷,打法稳中带攻。
3.下列各句中,加点的词语运用正确的一项是 A.近期鉴于银行保险理财纠纷、投资公司跑路方面的话题越来越多,作为拥有基金从业资格的证券从业人员,我觉得有必要给大家讲解几种常见的理财方式。
B.《数学的故事》是一部写给非专业人士看的数学史,正是因为这一读者定位,这本书没有循规蹈矩地平铺直叙,而是将数学置于一个更大的社会与历史背景中去描述。
C.无论写哪种文体,高考作文都不可写得十分隐讳,否则,容易导致阅卷老师误判。
D.在这个竞争日趋激烈的知识经济时代,如果胸无点墨、身无长物,是很难在社会上立足的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省严州中学2015届高三3月阶段测试文科数学试题一、选择题:本大题共8小题,每小题5分,共40分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
1.设全集U =R ,集合{|2},{|05},A x x B x x ==<≥≤错误!未找到引用源。
则集合错误!未找到引用源。
=A .错误!未找到引用源。
B .{|02}x x <≤错误!未找到引用源。
C .{|02}x x <≤错误!未找到引用源。
D .{|02}x x ≤≤错误!未找到引用源。
2.已知等差数列{}n a 满足:33,13133==a a ,则数列{}n a 的公差为A .1B .2C .3D .43.若π02x <<,则x x x cos sin <是1sin <x x 的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件4.设111()()1222b a <<<,那么 A .a b a b a a << B .b a a a b a << C .a a b b a a << D .a a b a b a <<5.已知角βα,均为锐角,且,31)tan(,53cos -=-=βαα=βtan 则 A .31B .139C .913D .36.已知平面向量,1),3,1(=-=→→→b a a 则→b 的取值范围是A .[]1,0B .[]3,1C .[]4,2D .[]4,37.已知定义在R 上的奇函数()f x =cx bax ++2的图象如图所示, 则c b a ,,的大小关系是 A .c b a >> B .b a c >> C .c a b >>D .b c a >>8.如图,已知双曲线C :22221x y a b-=()0,0>>b a 的右顶点为,A O为坐标原点,以A 为圆心的圆与双曲线C 的某渐近线交于两点Q P ,.若60PAQ ∠=︒且3OQ OP =,则双曲线C 的离心率为ABCD第Ⅱ卷二、填空题:本大题共7小题,前4小题每题6分,后3小题每题4分,共36分。
9.()的定义域为函数)4(g lo 22x x f -= ,值域为 ,不等式()1>x f 的解集为 . 10.一个简单几何体的三视图如图所示,其中正视图是一个正三角形,俯视图是等腰直角三角形,则该几何体的体积为 ,表面积为 .11.如果实数x,y 满足:20403x y x y x -⎧⎪+-⎨⎪⎩≥≥≤,则x y的取值 范围是 ,yx x y z +=的最大值为 .12.已知数列{}()112,(1)(1)2,,n n n a a n a n a n n *-=+=-∈N 满足:≥则=13a a ,数列{a n }的通项公式为 .13.已知点()0,2A ,()4,2-B ,()8,5C ,若线段AB 和CD 有相同的中垂线,则点D 的坐标是 . 14.在△ABC 中,角C B A ,,所对的边分别为c b a ,,,CD 是AB 边上的高,且222b c a <+,1sin sin 22=+B A ,则()=-B A sin .15.如图,在四棱锥ABCD P -中,底面ABCD 是平行四边形,点F E ,为PD PA ,的中点,则面BCFE 将四棱锥ABCD P -所分成的上下两部分的体积的比值为 .三、解答题:本大题共5小题,共74分。
解答应写出文字说明、证明过程或演算步骤。
16.(本题满分15分)在△ABC 中,角C B A ,,所对的边分别是c b a ,,,且满足:,)32()(22bc c b a -+-=又2cos 1sin sin CB A +=. (Ⅰ)求角A 的大小;(Ⅱ)若a =2,求△ABC 的面积S .(第15题图)17.(本题满分15分) 如图所示,四棱锥P -ABCD 中,底面ABCD 为菱形,且直线PA ⊥平面ABCD ,又棱PA =AB =2,E 为CD 的中点, 60=∠ABC . (Ⅰ) 求证:直线EA ⊥平面PAB ;(Ⅱ) 求直线AE 与平面PCD 所成角的正切值.18.(本题满分15分) 已知各项均为正数的数列{}n a 的前n 项和为n S ,且142-=n n a S . 在数列{}n b 中,21-=+n n b b ,1684-=+b b .(Ⅰ)求n a ,n b ; (Ⅱ)设nn nb c a =求数列{}n c 的前项和n T .19.(本题满分15分)已知抛物线的交点为()2,0P -. (Ⅰ)求抛物线Γ的方程;(Ⅱ)如图,()1,0Q ,过点P不同的两点,A B ,AQ 与BQ 分别与抛物线Γ交于点C ,D ,设AB ,DC 的斜率分别为12,k k ,,AD BC 的斜率分别为34,k k ,问:是否存在常数λ,使得1342k k k k λ=,若存在,求出λ的值,若不存在,说明理由.20.(本题满分14分) 已知函数23()4f x ax bx =+-()0>a ,4124)(++=b x g x x,且⎪⎭⎫ ⎝⎛+=a x f y 41为偶函数.设 集合{}11A x t x t =-+≤≤. (Ⅰ)若abt 2-=,记()x f 在A 上的最大值与最小值分别为N M ,,求N M -; (Ⅱ)若对任意的实数t ,总存在21,x x A ∈,使得12()()()f x f x g x -≥对[]1,0∈∀x 恒成立,试求a 的最小值.一、选择题:本大题共8小题,每小题5分,共40分。
二、填空题:本大题共7小题,前4小题每题6分,后3小题每题4分,共36分。
9.)2,2(-(]2,∞-()2,2-10.33 173++11.[2,31] 31012.61()14+n n 13.()7,614.1-15.53 三、解答题:本大题共5小题,共74分。
16.解:(1)∵,)32()(22bc c b a -+-=∴bc a c b 3222=-+,又∵23232cos 222==-+=bc bc bc a c b A ∴π6A = ——————————————7分(2)∵2cos 1sin sin CB A +=∴)cos(1cos 1sin sin 2B A C B A +-=+=,∴1sin sin cos cos =+B A B A 即1)cos(=-B A ————————————12分 ∴π0,6A B B A -===即,2π3C = 又∵C ab S a sin 21,2==∴3=S ——————————————15分17.解:(1)证明:∵∠ADE =∠ABC =60°,ED =1,AD =2 ∴△AED 是以∠AED 为直角的Rt △ 又∵AB ∥CD , ∴EA ⊥AB 又PA ⊥平面ABCD ,∴EA ⊥PA ,∴EA ⊥平面PAB , ——————————————7分 (2)如图所示,连结PE ,过A 点作AH ⊥PE 于H 点∵CD ⊥EA , CD ⊥PA∴CD ⊥平面PAE ,∴AH ⊥CD ,又AH ⊥PE ∴AH ⊥平面PCD∴∠AEP 为直线AE 与平面PCD 所成角————————11分 在Rt △PAE 中,∵PA =2,AE =3 ∴33232tan ===∠AE PA AEP ———————————15分18.解:(Ⅰ)由题意知0,212>+=n n n a S a 将1n =代入得211=a∴数列{}n a 是21为首项,2为公比的等比数列. 211122212---=⨯=⋅=n n n n a a ——————————4分 {}n b 为等差数列,公差为2-,684216b b b =-=+86-=∴b 即8101-=-b21=∴b n b n 24-= ———————————8分(Ⅱ)24216822n n n n n b n n c a ---=== nn n nn T 28162824...282028132-+-++-++=- …… ① 13228162824...202821+-+-+++=n n n n n T …… ② ——————10分 ①-②得1322816)21...2121(8421+--+++-=n n n nT nn n n n n nn 242816)211(442816211)211(218411112=----=----⋅-=+-+-n n nT 28=∴ ——————————————15分19.解:(Ⅰ) 28y x = ——————————4分(Ⅱ)假设存在实数λ设AB 的直线方程为2x my =-,211,8y A y ⎛⎫ ⎪⎝⎭,223,8y B y ⎛⎫ ⎪⎝⎭,233,8y C y ⎛⎫ ⎪⎝⎭,244,8y D y ⎛⎫⎪⎝⎭ 由228x my y x=-⎧⎨=⎩化简得:28160y my -+=所以1212816y y my y +=⎧⎨=⎩ ——————————7分2223111311,,,888y y y AQ y AC y y ⎛⎫⎛⎫=--=-- ⎪ ⎪⎝⎭⎝⎭由//AQ AC化简可得138y y =-,同理可得248y y =-——————————10分易得1128k y y =+,1223412128888y y k y y y y y y ===---+++,321412888k y y y y y ===+-,41238k y y y ==+ 所以代入1342k k k k λ=得128y y +12y y 1212y y y y λ=-+ 所以存在8λ=-——————————15分20.解:(1)⎪⎭⎫ ⎝⎛+=a x f y 41434161212-++⎪⎭⎫ ⎝⎛++=a b a x b ax 为偶函数, 所以21-=b .———————————2分 在区间]141,141[+-a a 上,)16143()41(),16143()141(aa f N a a a f M +-==+-=+=a N M =-∴ ———————————4分(2)设t x =2 ]2,1[2],1,0[∈=∴∈xt x()4122+-=t t x g 所以()x g 的最大值为41依题意原命题等价于 在A 上,总存在两个点12121,()()4x x f x f x -、使得≥即只需满足在A 上max min 1()()4f x f x -≥ ———————7分因为对任意的t 都成立,所以当abt 2-=也成立,由(1)知 14a ≥—————9分1)1(41)(412--==x x f a 时,当,下面证明在]1,1[+-t t 上总存在两点,21x x 、使得121()()4f x f x -≥成立.12max 1()[,1]111()()(1)()244t f x t t f x f x f t f t t +∴-+-=-当≥时,在上是增函数≥≥12max 1()[1,]311()()(1)()424t f x t t f x f x f t f t t <-∴---=->当时,在上是减函数≥综上所述,41的最小值为a . ——————————————14分。
