2点线
2-2 点、线、面的投影特性

2-2 点、线、面的投影特性一、点的投影1、点的三面投影点是组成物体最基本的几何元素。
如图2-9所示,在三投影面体系中,由空间点A(x,y,z)分别向三投影面作正投影,得其三面投影a(x,y)、a′(x,z)、a″(y,z),即过点A分别作三投影面的垂线,其垂足即为点A的三面投影;展开H面和W面,得到点A的三视图:a 、a′长对正,a′、a″高平齐,a 、a″宽相等,如图2-10所示。
图2-9 点的三面投影图2-10 点的三视图例1 :已知空间点B的两面投影b ,b′,如图2-11所示,求其第三面投影b″。
分析:空间点B的三面投影b 、b′、b″符合“长对正,高平齐,宽相等”的投影规律。
作图: b′与b″高平齐,b与b″宽相等,则其交点即为b″。
图2-11 求点的第三面投影图2-12 求点的三面投影例2 :已知空间点D(5,4,3),如图2-12所示,求其三面投影。
分析:空间点D的三面投影分别为d(x,y)、d′(x,z)、d″(y,z),且符合“长对正,高平齐,宽相等”的投影规律。
作图:分别在三投影轴上取x1=5,y1=4,z1=3,按“长对正,高平齐,宽相等”的投影规律分别作直线段,交点即为空间点D的三面投影(d 、d′、d″)。
2、两点的相对位置空间两点的相对位置是指空间两点间前后、左右、上下的位置关系。
两点在空间的相对位置可以根据两点的坐标值来判定,如图2-13所示。
X坐标确定两点的左右位置关系。
X坐标值大的点在左;Y坐标确定两点的前后位置关系。
Y坐标值大的点在前;Z坐标确定两点的上下位置关系。
Z坐标值大的点在上。
图2-13 两点的相对位置故A点在B点的右,后,上方,即B点在A点的左,前,下方。
3、重影点及其可见性判断若空间两点在某一投影面上的投影重合,则称这两点为该投影面的重影点。
此时,这两点位于同一投射线上,且有两个坐标的值分别相等,不等值的坐标之大小可以确定重影点的可见性,即X、Y、Z坐标值大的点分别位于左方、前方、上方,为可见点,如图2-14所示。
课件2:2.3.1 两条直线的交点坐标 ~2.3.2 两点间的距离公式

(2)轴对称: ①点 A(a,b)关于直线 Ax+By+C=0(B≠0)的对称点 A′(m,n), 则有mAn-·-a+ba2×m+-BAB·b=+2-n+1,C=0. ②直线关于直线的对称可转化为点关于直线的对称问题来解决.
32
[跟踪训练] 求直线 m:3x-2y-6=0 关于直线 l:2x-3y+1=0 的对称直线 m′ 的方程. 解:在直线 m 上取一点,如 M(2,0), 则 M(2,0)关于直线 l 的对称点 M′必在直线 m′上.
18
法二:∵kAC=1-7--13=32,kAB=3--3- -13=-23, 则 kAC·kAB=-1,∴AC⊥AB. 又|AC|= 1+32+7-12=2 13, |AB|= 3+32+-3-12=2 13, ∴|AC|=|AB|,∴△ABC 是等腰直角三角形.
19
[母题探究] (变设问)本例条件不变,求 BC 边上的中线 AM 的长. 解:设点 M 的坐标为(x,y),因为点 M 为 BC 的中点, 所以 x=3+2 1=2,y=-32+7=2,即点 M 的坐标为(2,2). 由两点间的距离公式得|AM|= -3-22+1-22= 26, 所以 BC 边上的中线 AM 的长为 26.
并求|PA|的值. 解:设点 P 的坐标为(x,0),则有
|PA|= x+32+0-42= x2+6x+25,
|PB|= x-22+0- 32= x2-4x+7.
由|PA|=|PB|,得 x2+6x+25=x2-4x+7,解得 x=-95.
故所求点 P 的坐标为-95,0.|PA|=
-95+32+0-42=2
则点(-1,-2)必在所求直线上,∴2×(-1)+3×(-2)+C=0,C=8.
∴所求直线方程为 2x+3y+8=0. [答案] (1)B (2)D
北师大版四年级上册第二单元线与角的知识点

北师大版四年级上册第二单元线与角的知识点线与角是数学中的基本概念,是几何学中的基本要素。
在四年级上册北师大版教材中,第二单元探讨了线与角的知识点。
下面将详细介绍这些知识点,帮助你更好地理解。
一、线的概念与分类线是几何学中的基本概念,是由无数个点连在一起形成的轨迹。
线有直线和曲线两种类型。
1.直线:直线是最简单的线,它由无数个点连在一起而成,方向是固定的,延伸无限远。
直线的表示方法有三种:-用字母表示:例如,直线AB可以表示为直线l;-用两个点表示:例如,直线AB也可以表示为点A和点B之间的直线;-用段落上一条小线段表示:例如,直线上的一小段可以表示为┍。
2.曲线:曲线是由无数个点连在一起而成,不同于直线的是它的方向是不固定的。
曲线的种类有很多,在这个单元里,主要涉及弧和线段。
二、角的概念与分类角是两条线、线段或射线相交并有共同端点的形态。
1.角的表示方法:角有两种表示方法:角的大小用度数来表示,角的位置用字母或符号表示。
2.角的分类:根据角的大小,可以将角分为:-零角:度数为0°的角,即两条射线重合在一起,形成一条直线;-直角:度数为90°的角,即两条线段相互垂直;-钝角:度数大于90°,小于180°的角;-锐角:度数小于90°的角。
三、角的度量度是我们用来度量角的单位,它来自于日常生活的360°一周的概念。
在度的基础上,教材还向学生介绍了角度的概念。
角度是度的一种更小的单位,由60个等分构成。
例如,一个直角是由90°角度构成的,它等于60°+30°。
四、角的比较教材中介绍了两种比较角大小的方法:按角的大小关系比较和直观感受大小。
1.按角的大小关系比较:-相等:两个角的度数相同;-互补:两个角的度数之和为90°;-互补角补角:两个角的度数之和为180°;-补角:两个互补角中较大的一个角叫做补角。
最新2024人教版七年级数学上册6.1.2 点、线、面、体--教案
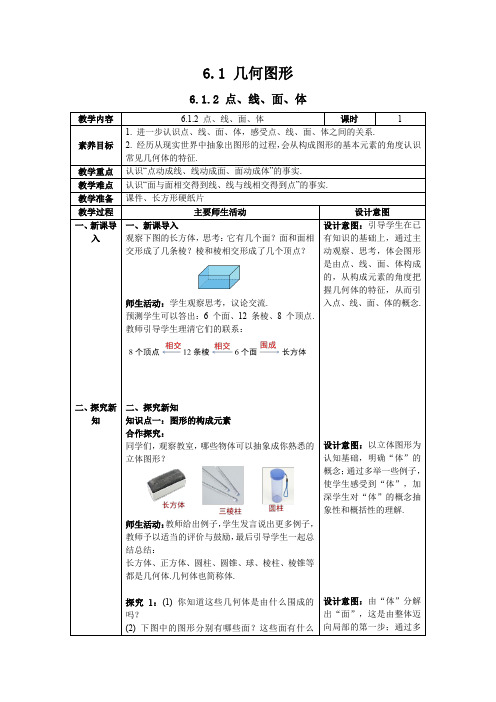
6.1 几何图形6.1.2 点、线、面、体一、新课导入观察下图的长方体,思考:它有几个面?面和面相交形成了几条棱?棱和棱相交形成了几个顶点?师生活动:学生观察思考,议论交流.预测学生可以答出:6 个面、12 条棱、8 个顶点.教师引导学生理清它们的联系:二、探究新知知识点一:图形的构成元素合作探究:同学们,观察教室,哪些物体可以抽象成你熟悉的立体图形?师生活动:教师给出例子,学生发言说出更多例子,教师予以适当的评价与鼓励,最后引导学生一起总结总结:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体.几何体也简称体.探究1:(1) 你知道这些几何体是由什么围成的吗?(2) 下图中的图形分别有哪些面?这些面有什么不同吗?师生活动:学生充分利用学具进行观察,并开展组内讨论,教师参与其中,老师引导学生归纳:1. 包围着的体是面.2. 面分为平的面和曲的面.想一想:探究2:面和面相交的地方形成了什么?它们有什么不同吗?师生活动:学生分小组探究;得出结论后,每小组派代表在全班交流;教师点评纠正,师生共同归纳:面和面相交的地方形成线,线有直线和曲线之分.探究3:线和线相交处又形成了什么?它们有什么不同吗?师生活动:借助前面的经验,教师引导学生归纳:线和线相交形成点.点只代表位置,没有大小,所以点都是相同的.想一想:立体图形的组成的元素包括什么?师生活动:教师引导学生进行归纳总结,并理清元素之间的联系,完成下图:例题精析:如图所示的立体图形是由________个平面和__________个曲面组成的,面与面相交形成__________条直线和举例和及时练习,加深学生对“面”的认识,理解“面”的概念.设计意图:借助“面”的学习经验进一步认识线和点,用合作探究的方式利于学生对概念的理解;引领学生完整经历“具体-抽象-具体”的认知过程,体会概念的产生和发展.设计意图:通过关系图的方式直观展示点线面体的关系,便于学生构建完整的知识框架.设计意图:通过练习巩固点、线、面、体的相关知_______条曲线.师生活动:学生独立思考,由学生代表发言,教师予以适当评价.知识点二:由点、线、面运动而形成的图形动手操作:画一画:把笔尖看作一个点,让这个点在纸上运动.观察结果,最终形成了什么?师生活动:学生画图并相互交流.教师追问1:通过画图,你得到了什么结论?请用精炼的语言加以概括.学生充分思考、讨论;教师引导学生归纳:点动成线.教师追问2:你能举出“点动成线”的生活实例吗?教师给出如下例子做示范,学生讨论,举出更多实例.画一画:把粉笔横着看作一条线,让这个粉笔在黑板上运动.观察结果,最终形成了什么?师生活动:教师通过现场操作粉笔并让学生观察黑板报,引发学生思考,学生代表回答,教师予以适当评价并引导学生归纳:线动成面.教师追问:你能举出“线动成面”的生活实例吗?教师给出如下例子做示范,学生列举更多实例.操作:长方形纸片绕它的一边旋转一周,会形成什么图形?识.设计意图:从动手实践中获得直观感受,在讨论交流中抽象概括,引导学生模拟知识发生、发展的过程,这种体验有利于学生学会学习.设计意图:从动手试验→观察思考→抽象概括,过渡到思考想象→猜想假设→实践验证,培养学生大胆猜想,小心求证的创新精神,在发展形象思维的同时培养空间想象力和几何直觉.设计意图:加深学生对面三、当堂练习师生活动:教师转动长方形纸片,然后由学生代表发言,老师可引导学生仿照前面的归纳得出结论:面动成体.教师可让各小组将纸片剪成不同形状(如:半圆、执教梯形、直角三角形),仿照老师刚才的操作并观察,再分别请小组代表展示转动过程与所得图形:练一练:1.(临沂期末改编)中华武术是中国传统文化之一,是中华民族在日常生活中结合多种传统文化思想,逐步形成了独具民族风貌的武术文化体系“枪挑一条线,棍扫一大片”,从数学的角度解释为( )A.点动成线,线动成面B.线动成面,面动成体C.点动成线,面动成体D.点动成面,面动成线师生活动:学生独立思考,由学生代表发言,教师予以适当评价.三、当堂练习1. 如图,三棱锥有____个面,它们相交形成了____条棱,这些棱相交形成了____个点.2. 请把下图中的平面图形与其绕轴旋转一周后得到的立体图形连接起来.动成体的理解,培养学生的观察能力和空间想象能力.设计意图:通过练习检测由点、线、面运动形成的图形知识掌握情况.设计意图:观察三棱锥的构成元素,提升迁移能力.设计意图:通过练习巩固由点、线、面运动形成的1.(东营期末改编)小翼跟妈妈到银行办理业务,她发现银行大堂的旋转门内部是由三块宽为 2 m、高为 3 m的玻璃隔板组成的,此情此景,她提出了以下问题:(1) 将此旋转门旋转一周,能形成的几何体是______.(2) 这能说明的事实是______(选择正确的一项填入).A. 点动成线B. 线动成面C. 面动成体(3) 求该旋转门旋转一周形成的几何体的体积.(边框及衔接处忽略不计,结果保留π)图形知识.设计意图:综合检测本节课所学的知识.板书设计点、线、面、体课后小结教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图.教学反思1.结合实例,鼓励学生探索学生虽然已经学习了立体图形和平面图形等几何概念,对于从具体事物或实例中进行数学抽象也有了初步认识,但点、线、面、体等都是很抽象的概念,与直观感受往往存在一定差距(例如平面是无限延展的,点没有大小只代表位置等内容),现阶段是难以深刻理解、完整认识的,所以要让学生充分活动起来,多观察,多举例,多表达.避免将这些抽象的概念强加给学生,要让学生在积累了丰富的直观感受后自发地同化概念,接受概念的意义.。
北师大版2024年新版七年级数学上册课件:1.1 课时2 点线面体

解:直角三角形绕其直角边所在直线旋转一周所形成的几何体 有两种情况:
解: (1)绕边长为8 cm的直角边所在直线旋转一周后得到圆锥, 如图, 其体积为 13×π×62×8= 96π(cm3).
解:(2)绕边长为6 cm的直角边所在直线旋转一周后得到圆锥, 如图, 其体积为 13×π×82×6= 128π(cm3).
探究新知
思考:圆柱和球可以看成由哪个平面图形旋转得到?
圆柱可以看成由长方形 旋转得到.
球可以看成由半圆 旋转得到.
注意: 一般地,含有曲面的几何体,都可以看成由某一平面图形绕着某一 旋转轴旋转一定的角度得到. 旋转轴或旋转角度不同,所得到的 几何体不一定相同.
探究新知
例1 图中各个花瓶的表面可以大致看成由哪个平面图形绕 虚线旋转一周而得到?用线连一连.
课堂练习
3.判断题
(1)围成球的只有一个曲面.
()
(2)一个长方形绕一条边旋转一周形成一个长方体. ( )
(3)圆锥上有一个顶点、一条曲线、一个平的面、一个曲的面.
(4)用圆规画圆的过程就是一个点动成线的实例.
() ()
分析:长方形绕一条边旋转一周形成一个圆柱.
课堂练习
4.想象下列平面图形绕轴旋转一周,可以得到哪些立体图形?
点 线面
· 面与面相交得到线, 线与线相交得到点.
点无大小,线无粗细,面无厚薄.
探究新知
找出图中的点、线、面.
找出图中的点、线、面. 点
找出图中的点、线、面. 曲的
哪些线是直的? 哪些线是曲的?
直的 线
找出图中的点、线、面. 平面
哪些面是平的? 哪些面是曲的?
面 曲面
探究新知
观察六棱柱和圆柱,回答下列问题. (1)六棱柱是由几个面围成的? 圆柱是由几个面围成的? 它们都是平的吗?
过2点与直线相切的圆的分析与图解

假设 过点 A , 、 , 且与圆 0 相切 的 圆为 0 。
作图依据 : 确定 l 共轴圆组 ; 圆0 , 是该共 轴圆
组 中的一 个 圆 ; 以定点 A 、 B , 为 公共 点 的共轴 圆组 中
任意圆与已知圆 0 的根轴( 等幂轴 ) 必通过 1 定点,
An a l y t i c a l Pr o o f a n d I l l u s t r a t i o n s f o r Ci r c l e s P a s s i n g Th r o u g h
Two Gi v e n Po i n t s a nd Ta n g e nt t o A Gi v e n Li n e
尼奥斯 问题 的特 殊情 况 。当其 中 1圆或 者 多 圆退 化
当 2点连线 与 已知直 线倾 斜时 , 过 已知 2点 可作
如 图 3所 示 。此 时 , 2圆的半 成点 或 者 直 线 时 , 又 可 以衍 生 出该 问 题 的 多种 特 殊 2个 圆与 已知直 线相切 ,
下面对这种 隋况下 的图解方 法进行讨论 。 情况 。某 些特 殊 情 况 不 能 采 用 一 般 情 况 下 的 解 法 。 径不相 等 , 本文 所探 讨 的解 法 为 3圆 中 的 2圆退化 成 点 且 另 1 圆退 化成 直线 的情 况 。该 解 法 丰富 了 阿 波罗 尼 奥斯
该定 点 位 于直线 A , 曰 , 上( 根 据反 演理论 ) ;
结论 : 圆D , 与 已知圆 0 的根轴将与直线 A , B , 交于 l 点。 假设该点为点 P 。下面求作点 P 。 过点 A , 、 , 任作 1 圆D , 作出圆 D 与圆 0 £
机械工程制图教程2-2点、线、面的投影

点的投影
point
过空间点A作投射线与投 影面P的交点,即为点A在P面 上的投影。
P
●
A
a
●
P
点在一个投影面上的投影 不能确定点的空间位置。
B1
B2
B3
●
●
b
●
●
重影coincidence of projection
上海理工大学《机械制图》课件(C版)
一、点在三投影面体系中的投影
1、三投影面体系的建立
(1)水平面
V
a A b c B
a
b a
b
c
b
a
c
C b a
实形true shape
c
W
b a
H
c
c
投影特性: 1、ab c∥X轴,abc∥Y轴,均为积聚性投影; 2、水平投影abc反映ABC实形。
●
az
ax
X
A
O
ax
●
a
W
a
●
Y
ay
a● H
ay
Y
4.点的投影规律:
(1)点的正面投影与水平投影的连线a a⊥OX轴; (2)点的正面投影与侧面投影的连线a
a
长对正
⊥OZ轴;
高平齐
(3)点的水平投影到OX轴的距离与点的侧面投影到 宽相等 OZ轴的距离相等,即aax= a aZ 。
为了作图方便,可过原点O作YOY的角平分线,则aaY与a aY的延长线必与这条辅助线 交于一点,从而体现aaz=aax 的对应关系。
2.投影面垂直线 perpendicular line 垂直于一个投影面而平行于另两个投影面的直线。 可分为: 铅垂线----垂直于H面,平行于V、W面的直线; 正垂线----垂直于V面,平行于H、W面的直线; 侧垂线----垂直于W面,平行于V、H面的直线。
《机械制图》教案——第二章-2 点线面的投影

点、直线和平面的投影教学目的要求:1.点的投影及作图.2.各种位置直线的投影,及两直线的相对位置.3.直角三角形法求直线的实长和倾角,直角定理.4.各种位置平面的投影,平面上取点取线的作图.教学重点难点:1.各种位置直线的投影.2.各种位置平面的投影.3.平面上取点取线的作图.学时: 3§ 1点的投影1.1点的三面投影本节教学目标:点在第一分角中各种位置的投影特性和作图方法。
重点:点在两投影面体系及三投影面体系中的投影,两点的相对位置及重影点的投影。
难点:重影点的投影。
引入:点是最基本的几何元素,以此来分析点在空间中的位置关系及规律。
1.1.1三面投影的规律点的三面投影:水平投影 a → H正面投影 a´→ V侧面投影 a″→ W点的三面投影规律:a′a ⊥ oxa′a″⊥ oza aх =a″az1.1.2点的投影与坐标的关系一、三投影面体系中点的投影A a = a′ax = a″ay = 高标(Z标)A a′= a ax = a″az = 纵标(Y标)A a″= a′az = aay = 横标(X标)V、H 投影反映XV、W 投影反映ZH、W 投影反映Y1.点在三投影面体系中的投影空间点 A的位置确定后,那么它的三面投影( a、a′、 a″)投影就确定了,反之如果空间一点的三面投影确定,则空间点的位置也就确定。
2.术语及规定习惯上我们将空间点用大写的字母表示,其投影用相应的小写字母表示。
3.投影性质点的两投影的连线垂直于相应的投影轴;点的投影到投影轴的距离反映空间点到投影面的距离。
二、特殊位置点的投影1.其他分角内的点两投影面体系——四分角;三投影面体系——八分角。
2.其他情况投影面上的点的投影关系;投影轴上的点的投影关系1.2两点的相对位置和重影点1.2.1两点的相对位置根据两点相对于投影面的坐标不同,即可确定两点的相对位置。
XA<XB B点在A左方 YA>YB B点在A点后方 ZA>ZB B点在A点下方例:比较三棱锥四个顶点S、A、B、C的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
铅垂线
Z a A b a
a
b X
Z
a
b
X
O
YW
O B a(b)
b a(b)
a b OY
Y
2、 a bOX ;
YH
3、 a b = a b = AB
投影特性:1、a b 积聚 成一点
正垂线
Z ab A B O a b Y
ab
z
a
b
a
b X a O YW
b
b
a X A a
O b
O
a’’ YW
一、直角三角形法的作图要领 用线段在某一投影 面上的投影长作为一条直角边,再以线段的两端点 相对于该投影面的坐标差作为另一条直角边,所作 直角三角形的斜边即为线段的实长,斜边与投影长 间的夹角即为线段与该投影面的夹角。 二、直角三角形的四个要素 直角三角形的四个要 素即:实长、投影长、坐标差及直线对投影面的倾 角。已知四要素中的任意两个,便可确定另外两个。
投影面垂直线
一般位置直线
一般位置直线 Z
b
B b a X
b
Z
b
a
X A a
O b a
O b
a Y
Y a Y
一般位置直线投影特性
投影特性:1、a b、 ab、a b均小于实长 2 、a b、ab、a b均倾斜于投影轴 3 、 不反映 、 、 实角
例题4 已知 线段的实长AB,求它的水平 投影。
AB
b
|zA-zB|
AB |zA-zB|
a
X
ab
b
ab AB |yA-yB|
a
ab
直线上的点
c
b B C X a A O
直线上的点具有两个特性:
c b c
a
1 从属性 若点在直线上,则点的各个投影必在直线的各同面投影上。利用 这一特性可以在直线上找点,或判断已知点是否在直线上。
a
H
a
点的两面投影图性质 a A V
V
a
zA
X
ax a
O
X
ax yA
xA
O
H
a H
1)aaOX 2) aax =Aa = zA , aax =Aa = yA
形体的三面投影图
在这个三投影面体系中,水平放置的平面称为水平投影面 (简称水平面,用H表示),正对着观察者的投影面称为正立面 投影(简称立面,用V表示),第三个投影面在观察者右侧,称 为侧立投影面(简称侧面,用W表示),三投影面两两相交构成 三条投影轴OX、OY、OZ,三轴的交点O称为原点。
b
k
d
a d
两直线交叉
空间两直线若既不平行又不相交时, 则称为交叉(又称异面直线)。交叉两直线 的同面投影也可能相交,但各个投影的交 点不符合一点的投影规律。
两直线交叉
d d b
1(2) a X A a 2 C c 1 c 2
b
B D O b 1 d
1(2) a c
X
垂直相交的两直线的投影
a A
b
B
C c X a b H
c
a c b
AB垂直于AC,且AB平行于H面,则有ab ac
交叉垂直的两直线的投影 定理三: 相互垂直的两直线,其中有一条 直线平行于投影面时,则两直线在该投影面 上的投影仍反映直角。 定理四: 两直线在同一投影面上的投影反 映直角,且有一条直线平行于该投影面,则 空间两直线的夹角必是直角。
a H
2. aa ox aa oz
YH
投影面和轴上的点投影
V
Байду номын сангаас
b
V
Bb a X
a c O b O H c
X b H
Cc c
Aa
a
例题1
已知点A的正面与侧面投影,求点A的水平投影。
Z a a
X
O
YW
a YH
a
Z
a
注:因为 平面是无 限大的, 所以一般 不画出平 面边框。
垂直交叉的两直线的投影
A B N
a X m a
n
b
C a
c
n
n b H m
b B
D X
C
a
a X
A a
b b a c
d
b c
两直线相交
两相交直线在同一投影面上的投影仍 相交,且交点属于两直线。 反之,若两 直线在同一投影面上的投影相交,且交点 属于两直线,则该两直线相交。
两直线相交 d
d k B b
b
k a X c
C Ac a K D
a
X
c c b k
水平线 z
Z
a
b
a
b
a
A
b
a
X
O
YW
B
X
O
b
a
a
b
Y
b
投影特性:1、ab OX ; ab OYW 2、ab=AB 3、反映、 角的真实大小
YH
正平线
Z b b
Z
b
a
B a b
a
X
O
a
YW
A
X
O
a
b
Y
a
2、a b=AB
形体的三面投影图
为了更真实的反映形体的情况,我们一般把形体放在三个 互相垂直的平面所组成的投影面体系中进行投影。
形体的三面投影图
三面投影图的形成
形体的三面投影图
三面投影图的投影关系 “长对正、 高平齐、宽相 等”是三面投影
图最基本的投影 规律,它不仅适 用于整个群体的 投影,也适用于 形体的每个局部 的投影。
X
O
Y
a
Y
点的投影与坐标
若把三个投影面当作空间直角坐标面,投影 轴当作直角坐标轴,则点的空间位置可用其(X、 Y、Z)三个坐标来确定,点的投影就反映了点的 坐标值,其投影与坐标值之间存在着对应关系。
点的一个投影反映了点的两个坐标。已知点 的两个投影,则点的X、Y、Z三个坐标就可确定, 即空间点是唯一确定的。因此已知一个点的任意 两个投影即可求出其第三投影。
直
两
点的投影
两面投影体系的建立
V
X
水平投影面 —— H
垂直投影面 —— V 投 影 轴 —— OX
第 一 分 角
H
O
点的两面投影
V
a
zA
A
xA yA
X
O
H A点的水平投影 —— a
A点的垂直投影 —— a
a
点的两面投影图画法 a A V a
V
zA
O X
X
ax
ax yA
xA
O
H H
a X
b
c
a
2-3直线的相对位置
平行 相交——垂直 交叉——垂直
2-3直线的相对位置
直线平行
若空间两直线相互平行,则其各同面投影 必然相互平行且比值不变。反之,如果两直线 的各同面投影相互平行且比值相等,则此两直 线在空间也一定相互平行。
两直线平行 b d c d c
a H
a W
ay
Y
例2 已知点A(15,16,12),求作其三面投影
点的相对位置
Z a b O YW a
Z a a X b b a
两点中X 值大的点 ——在左 两点中Y 值大的点 ——在前 两点中Z 值大的点 ——在上
b X B b O
b
A
Y
a
YH
例题3 已知A点在B点之右8毫米,之前5毫米,之上9 毫米,求A点的投影。 Z
X
b
ab OZ 3 、 ab = ab =AB
投影特性: 1、 ab积聚 成一点 2 、 ab OX ;
YH
侧垂线
Z a b ab A
a
b
Z
ab
X
B O
X
O
YW
a a b Y
2 、 ab OYH ;
b YH
ab OZ 3 、 ab = ab =AB
b
2
a
c
d
1
例题6
判断两直线的相对位置
c
b
z
c
b
a X
a
d o d b c
a
d
YW
YH
直角投影
垂直相交的两直线的投影 定理一: 垂直相交的两直线,其中有一条直线平行于投影面时, 则两直线在该投影面上的投影仍反映直角。 定理二: 相交两直线在同一投影面上的投影反映直角,且有一条 直线平行于该投影面,则空间两直线的夹角必是直角。
点的投影与坐标
Aa″=a′aZ = aayh =x坐标; Aa′=aaX = a″aZ =y坐标; Aa =a′aX = a″ ayw =z坐标。 点的每个投影反映两个坐标, 点的三面投影与点的坐标关系为: (1)A点的H面投影a Z V 可反映该点的x和y坐标; az a (2)A点的V面投影a′ y 可反映该点的X和Z坐标; x (3)A点的W面投影a″ ax O X 可反映该点的y和Z坐标。 z
a X A a
C
b
O
X
AB
求直线的实长及对V面倾角 b B AB b
