2016春季班尖子班第8讲讲义-数学-点线排布

合集下载

高一数学春季尖子班讲义第12讲圆的初步教师版尖子班

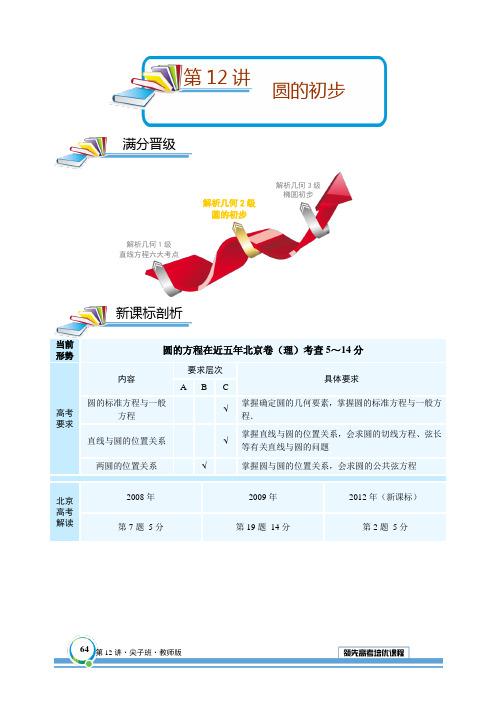
当前形势圆的方程在近五年北京卷（理）考查5～14分高考要求内容要求层次具体要求A B C圆的标准方程与一般方程√掌握确定圆的几何要素，掌握圆的标准方程与一般方程．直线与圆的位置关系√掌握直线与圆的位置关系，会求圆的切线方程、弦长等有关直线与圆的问题两圆的位置关系√掌握圆与圆的位置关系，会求圆的公共弦方程北京高考解读2008年2009年2012年（新课标）第7题5分第19题14分第2题5分新课标剖析满分晋级第12讲解析几何1级直线方程六大考点解析几何2级圆的初步解析几何3级椭圆初步圆的初步【教师备案】因为直线方程建议讲了4小时，所以本讲建议讲2小时考点1：圆的标准方程1. 圆的标准方程 ⑴以点()C a b ，为圆心，r 为半径的圆的方程：222()()x a y b r -+-= ⑵圆心在原点的圆的标准方程：222x y r +=【教师备案】⑴我们知道，平面内到一定点的距离等于定长的点的轨迹是圆，定点是圆心，定长是圆的半径．现在我们来求以()C a b ，为圆心，r 为半径的圆的方程．设()M x y ，是C e 上的任意一点．点M 在C e 上的条件是CM r =．也就是说，如果点M 在C e 上，则CM r =，反之，如果CM r =，则点M 在C e 上．由两点间的距离公式，所说条件可转化为方程表示：()()22x a y b r -+-=．两边平方，得()()222x a y b r -+-=①．显然，C e 上任意一点M 的坐标()x y ，适合方程①；如果平面上一点M 的坐标()x y ，适合方程①，可得CM r =，则点M 在C e 上．因此方程①是以点()C a b ，为圆心，r 为半径的圆的方程，叫做圆的标准知识切片知识点睛12.1圆的方程M COyxP (x, y )r Oy x方程．特别地，如果圆心在坐标原点，这时00a b ==，，圆的标准方程就是222x y r +=． ⑵圆的标准方程()()222x a y b r -+-=⇔圆心()a b ，，半径为r ，它体现了圆的几何性质，圆的标准方程直接给出了圆的圆心坐标和半径长，突出了确定一个圆的基本要素，因此，有利于画出图形．⑶圆的标准方程中共有三个待定系数a b r ，，，只要确定出这三个量的值，圆的方程即被确定．因此确定圆的方程需要三个独立的条件，其中圆心是圆的定位条件，半径是圆的定形条件．⑷方程()()22x a y b t -+-=：①当0t >时，表示圆心为()C a b ，t ②当0t =时，表示一个点()C a b ，； ③当0t <时，不表示任何图形．2. 点与圆的位置关系圆的标准方程()()222x a y b r -+-=，圆心()A a b ，，半径r ，若点()00M x y ，在圆上，则()()22200x a y b r -+-=；若点()00M x y ，在圆外，则()()22200x a y b r -+->；若点()00M x y ，在圆内，则()()22200x a y b r -+-<；反之，也成立．【教师备案】判断点与圆的位置的方法是由两点间的距离公式，求出该点到圆心的距离，再与圆的半径比较大小即可．例：写出圆心为()23A -，，半径长等于5的圆的标准方程，并判断点()157M -，，()251M --是否在这个圆上，若不在这个圆上，是在圆内还是在圆外？【解析】圆心为()23A -，，半径长等于5的圆的标准方程是()()222325x y -++=．把()157M -，的坐标代入上述方程中，有()()22527325-+-+=，即点1M 的坐标适合圆的方程，可知点1M 在这个圆上；把()251M -的坐标代入上述方程中，有()()225213134525--+-+=+，可知点2M 不在这个圆上，而在这个圆内．3. 确定圆的方法要求出圆的标准方程必须求出圆心和半径．确定圆的标准方程的主要方法是待定系数法，即列出a b r ，，的方程组，一般步骤为： ⑴根据题意，设所求的圆的标准方程()()222x a y b r -+-=；⑵根据已知条件，建立关于a b r ，，的方程组； ⑶解方程组，求出a b r ，，的值，并把它们代入所设的圆的方程中，就得到所求圆的方程．条件方程形式过原点 ()()()2222220x a y b a b a b -+-=++≠ 圆心在x 轴上 ()()2220x a y r r -+=≠圆心在y 轴上 ()()22220x y b r r +-=≠圆心在x 轴上且过原点()()2220x a y a a -+=≠圆心在y 轴上且过原点()()2220x y b b b +-=≠与x 轴相切 ()()()2220x a y b b b -+-=≠与y 轴相切 ()()()2220x a y b a a -+-=≠与两坐标轴都相切()()()2220x a y b a a b -+-==≠【例1】圆的标准方程写出下列各圆的方程⑴经过点()63，，圆心为()22-，；⑵经过点()45A --，，()61B -，，且以线段AB 为直径．【解析】 ⑴所求圆的方程为()()222241x y -++=⑵所求圆的方程为()()221329x y -++=【备选】求以两直线1:5l x y -=，2:24l x y +=的交点为圆心，且与x 轴相切的圆的标准方程．【解析】所求圆的标准方程为()()22324x y -++=．考点2：圆的一般方程1．圆的一般方程220x y Dx Ey F ++++=，（2240D E F +->）说明：⑴2x 和2y 项的系数相等且都不为零；⑵没有xy 这样的二次项．⑶表示以,22D E ⎛⎫-- ⎪⎭为圆心，22142D E F +-为半径的圆．例：二元二次方程22232340x y x y +-++=是否表示圆．【解析】 ∵2x 和2y 的系数不相等，∴方程不表示圆．【教师备案】将圆的标准方程()()222x a y b r -+-=展开，得22222220x y ax by a b r +--++-=，由此可见，圆的方程具有如下形式：()220x y Dx Ey F ++++=*，其中D E F ，，为常数．那么，形如()*的方程是否都表示圆呢？将方程220x y Dx Ey F ++++=配方，得()222214224D E x y D E F ⎛⎫⎛⎫+++=+- ⎪ ⎪⎝⎭⎝⎭，与圆的标准方程比较，可知：经典精讲知识点睛①当2240D E F +->时，方程()*表示以22DE ⎛⎫-- ⎪⎝⎭，为圆心，22142D EF +-为半径的圆；②当2240D E F +-=时，方程()*只有一个解，表示一个点22DE ⎛⎫-- ⎪⎝⎭，；③当2240D E F +-<时，方程()*无实数解，它不表示任何图形．例：若220x y x y m +-+-=表示一个圆的方程，则m 的取值范围是（）A ．12m >-B ．12m -≥ C ．12m <- D ．2m >-【解析】 A2．如何选用圆的方程圆的方程有标准方程和一般方程，求哪一种都需要三个独立条件，都要用到待定系数法，但要灵活选用圆的方程的形式，以便简化计算．一般来说．⑴如果由已知条件容易求得圆心坐标、半径或需利用圆心的坐标或半径来列方程的问题一般采用圆的标准方程，再用待定系数法求出a b r ，，；⑵如果已知条件和圆心或半径都无直接关系，一般采用圆的一般方程，再利用待定系数法求出常数D E F ，，．例：⑴求经过两点()14A -，、()32B ，且圆心在y 轴上的圆的方程；⑵求过三点(11)A -，，(14)B ，，(42)C -，的圆的方程，并求这个圆的半径和圆心坐标．【解析】 ⑴ 圆的方程是()22110x y +-=．⑵所求圆的方程为227320x y x y +--+=．半径522r =，圆心7322⎛⎫⎪⎝⎭，【教师备案】老师可以配合知识点睛中的例子先讲圆的一般方程以及一般方程表示圆的条件，然后让学生做例2以及相应班次的学案；最后再根据知识点睛中的例子讲如何选用圆的方程，然后再做例3和相应班次的学案．【例2】方程220x y Dx Ey F ++++=表示圆的条件判断下列方程是否表示圆，若是，求出圆心和半径⑴ 22104x y x +-+=；⑵ ()22200x y ax a ++=≠；⑶ 22210x y ay ++-=；【追问】若表示圆，则当圆的面积最小时，a 的值为多少？ ⑷ 22220160x y x +++=．经典精讲⑸ 224250x y mx y m ++-+=【解析】解法一：⑴22102x y ⎛⎫-+= ⎪⎝⎭表示一个点，坐标为102⎛⎫⎪⎝⎭，；⑵()()2220x a y a a ++=≠表示圆，圆心()0a -，，半径r a =； ⑶()2221x y a a ++=+表示圆，圆心()0a -，，半径21r a =+；【追问】当0a =时，圆的面积取最小值． ⑷()22221010160x y ++=-<，不表示任何图形． ⑸1m >或14m <时表示圆，圆心为()21m -，，半径为2451m m -+．当114m ≤≤时，方程不表示圆．【备选】若直线530x y -+=经过圆2222104m x y mx y +-++-=的圆心，则m 等于（）A ．16-B ．16C ．0或16D ．0或16-【解析】 A【例3】求圆的一般方程⑴已知ABC △三边所在直线方程:60AB x -=，:280BC x y --=，:20CA x y +=，求此三角形外接圆的方程．⑵求过原点及()11A ，且在x 轴上截得的线段长为3的圆的方程．【解析】 ⑴222143002x y x y +-++=． ⑵所求圆的方程为22350x y x y ++-=或2230x y x y +-+=．考点3：直线与圆的位置关系1．直线与圆的位置关系：①直线与圆相交，有两个公共点； ②直线与圆相切，有一个公共点；知识点睛12.2直线（圆）与圆的位置关系③直线与圆相离，没有公共点．2．直线与圆的位置关系的判定有两种方法：①代数法：判断直线0Ax By C ++=和圆220x y Dx Ey F ++++=的位置关系，可将2200Ax By C x y Dx Ey F ++=⎧⎨++++=⎩消去y （或x ），得20mx nx p ++=（或20my ny p ++=）．当0∆>时，直线与圆相交，有两个公共点；当0∆=时，直线与圆相切，有一个公共点；当0∆<时，直线与圆相离，无公共点．②几何法：已知直线0Ax By C ++=和圆()()222x a y b r -+-=，可用圆心到直线的距离22Aa Bb Cd A B++=+与r 的大小关系判断直线与圆的位置关系．当d r <时，直线与圆相交，有两个公共点；当d r =时，直线与圆相切，有一个公共点；当d r >时，直线与圆相离，无公共点；<教师备案>一般的，判定直线与圆的位置关系都用几何法，代数法在圆锥曲线才会常用。

2016春季班尖子班第11讲讲义-最短路线

B
C
A
4
三年级春季第 11 讲标数法（B 版）
【答案】100 【分析】标数法如图．
B 10 40 100 10 30 60 10 20 30 C 1 3 6 10 10 10 1234 A 111 1
一只蜜蜂从 A 处出发，回到家里 B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？
养老院
市中心
学校
（1）他们从学校经过市中心到养老院的最短路线共有
2
三年级春季第 11 讲标数法（B 版）
几条呢？（2）若他们不经过市中心到养老院的最短路线共有几条呢？（3）傍晚时，市中心附近下了一场大雨，附近的路均无法通行，请问到养老院的最短路线共有几条呢？(仅出现在教师版)
1
家
1
1
1
1
2
3
4
1
3
6
10
4
10
20
1
学而思
小君家到学校的道路如图所示．从小君家到学校有________种不同的走法．（只能沿图中向右向下的方向走）
小君家
学校
【答案】10 【分析】标数法如图，共 10 条不同走法．
小君家
1
1
1
1
2
2
1
3
1
1
2
2
3
4
7
10
学校
艾迪和薇儿准备去看望养老院的李奶奶，如下图：
养老院
市中心
学校
【答案】60；66；35 【分析】（1）采用标数法（如图）．可得从学校到养老院共有 60 种走法．
1
3
1 2
学校 1

初一数学人教版秋季班(教师版)第7讲规律探索--尖子班

第7讲规律探究⎧⎨⎩数字类规律探究图形类知识点1：规律探究之数字变化数字的变化问题一般有找循环周期、等差数列、等比数列、平方数等类型。

【典例】1.如图，是蜘蛛结网过程示意图，一只蜘蛛先以O 为起点结六条线OA ，OB ，OC ，OD ，OE ，OF 后，再从线OA 上某点开始按逆时针方向依次在OA ，OB ，OC ，OD ，OE ，OF ，OA ，OB…上结网，若将各线上的结点依次记为：1，2，3，4，5，6，7，8，…，那么第2016个结点在（）A. 线OA 上B. 线OB 上C. 线OC 上D. 线OF 上【解析】解：根据数的排布发现：1在OA 上，2在OB 上，3在OC 上，4在OD 上，5在OE 上，6在OF 上，7在OA 上，…，射线上的数字以6为周期循环， ∵2016÷6=336，∴2016与6在同一条射线上，即2016在射线OF 上．故选：D 【方法总结】遇到循环节问题首先找到循环节（循环周期）是什么，循环节可以通过将图形中的元素一一列举得到；其次要找到所求元素所在的循环节；最后找到在循环节中的位置。

2.一组数23，45，67，89…按一定的规律排列着，请你根据排列规律，推测这组数的第10个数应为_____【解析】解：设该数列中第n 个数为a n （n 为正整数），观察，发现规律：a 1=23，a 2=45，a 3=67，a 4=89，…，∴a n =2n2n+1．当n=10时，a 10=2×102×10+1=2021．【方法总结】等差数列问题首先找出公差，即后一项与前一项的差，其次用第一项与公差、序号来表示每一项；遇到分数数列，如果找不到公差，可以考虑将分子、分母作为两个不同的数列分别找出其中的规律，最后确定数字的正负与序号奇偶的关系。

3.下面是一组按规律排列的数：1，2，4，8，16，…，则第2008个数是_______ 【解析】解：第1个数1=1，第2个数2=21，第3个数4=22，第4个数8=23，第5个数16=24， …，第2008个数是：22007．【方法总结】等比数列问题首先找出后一项与前一项的比值；其次通过列举观察、用第一个数字和公比来表示每一个数字。

初一上数学春季班讲义(尖子)

第一讲平行线的判定及性质【课程导航】1. 两条不同的直线，若它们只有一个交点，就可以说它们相交，即两直线相交有且只有一个交点.2. 垂直是相交的特殊情况，关于垂直有两个重要的结论： ⑴过一点有且只有一条直线与已知直线垂直；⑵直线外一点与直线上所有点连成的线段中，垂直线段最短. 3. 在同一平面内，不相交的两条直线称为平行线。

关于平行线，应理解平行公理，即过直线外一点，有且只有一条直线与已知直线平行.4. 两条直线被第三条直线所截，得到八个角，其中有四对同位角，两对内错角，两对同旁内角，这就是“三线八角”.5. 在同一平面内，不重合直线的位置关系是相交或平行.【锦囊妙计】1.能熟练地找出图形中的三线八角.2.运用平行线的性质定理： ⑴两直线平行，同位角相等； ⑵两直线平行，内错角相等； ⑶两直线平行，同旁内角互补；⑷如果一条直线和两条平行线中的一条垂直，那么它和另一条也垂直. 3.运用平行线的判定定理： ⑴同位角相等，两直线平行； ⑵内错角相等，两直线平行； ⑶同旁内角互补，两直线平行；⑷在同一平面内，平行于同一直线的两条直线平行； ⑸在同一平面内，垂直于同一条直线的两条直线平行.【典型例题】例1．已知：如图，∠BED ＝85°，∠B ＝35°，∠D ＝50°，求证：AB ∥CD ．思路点拨：过点E 作EF ∥AB ，则∠BEF ＝∠B ＝35°，易得∠FED ＝50°，所以∠FED ＝∠D ，即可证明EF ∥CD ，则AB ∥CD .解答：证明：过点E 作EF ∥AB ，∴∠BEF ＝∠B ＝35°（两直线平行，内错角相等）， ∵∠BED ＝85°，∠D ＝50°，∴∠FED ＝50°，∴∠FED ＝∠D ＝50°，∴EF ∥CD （内错角相等，两直线平行），∴AB ∥CD （同一平面内，平行于同一直线的两直线平行）．点评：此题考查平行线的判定和性质：两直线平行，内错角相等；内错角相等，两直线平行；同一平面内，平行于同一直线的两直线平行．要灵活应用．例2．如图，∠AEM ＝∠DGN ,∠1＝∠2,证明EF ∥GH .思路点拨：证明两条直线平行，需找同位角或内错角相等或同旁内角互补，想办法将题目中的相等角转化成我们需要的角即可。

著名机构数学讲义寒假08-七年级基础版-三线八角--学生版

教师姓名冯娜娜学生姓名年级初一上课时间单击此处输入日期。

学科数学课题名称三线八角知识模块Ⅰ：同位角、内错角、同旁内角的概念1、“三线八角”模型如图，直线AB、CD与直线EF相交(或者说两条直线AB、CD被第三条直线EF所截)，构成八个角，简称为“三线八角”，如图1.三线八角图1注意：⑴两条直线AB,CD与同一条直线EF相交．⑵“三线八角”中的每个角是由截线与一条被截线相交而成．2. 同位角、内错角、同旁内角的定义在“三线八角”中，如上图1，（1）同位角：像∠1与∠5，这两个角分别在直线AB、CD的同一方，并且都在直线EF的同侧，具有这种位置关系的一对角叫做同位角.（2）内错角：像∠3与∠5，这两个角都在直线AB、CD之间，并且在直线EF的两侧，像这样的一对角叫做内错角.（3）同旁内角：像∠3和∠6都在直线AB、CD之间，并且在直线EF的同一旁，像这样的一对角叫做同旁内角.注意：(1)“三线八角”是指上面四个角中的一个角与下面四个角中的一个角之间的关系，显然是没有公共顶点的两个角.(2)“三线八角”中共有4对同位角，2对内错角，2对同旁内角．知识模块Ⅱ：同位角、内错角、同旁内角位置特征及形状特征注意：巧妙识别三线八角的两种方法：(1)巧记口诀来识别：一看三线，二找截线，三查位置来分辨.(2)借助方位来识别根据这三种角的位置关系，我们可以在图形中标出方位，判断时依方位来识别，如图2．【例1】 (1)图1中，∠1、∠2由直线被直线所截而成．(2)图2中，AB为截线，∠D是否属于以AB为截线的三线八角图形中的角？图1图2【例2】如图，(1)DE为截线,∠E与哪个角是同位角?(2)∠B与∠4是同旁内角，则截出这两个角的截线与被截线是哪些直线？(3)∠B和∠E是同位角吗?为什么?【例3】如图，用数字标出的八个角中，同位角、内错角、同旁内角分别有哪些？请把它们一一写出来．【例4】分别指出下列图中的同位角、内错角、同旁内角.【例5】如图直线DE、BC被直线AB所截，(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角？每组中两角的大小关系如何？(2)如果∠1=∠4，那么∠1和∠2相等吗？∠1和∠3互补吗？为什么？【习题1】如图，直线AD、BC被直线AC所截，则∠1和∠2是( ).A．内错角B．同位角C．同旁内角D．对顶角∠构成同位角的有( ).【习题2】如图，能与αA．4个B．3个C．2个D．1个【习题3】如图，下列说法错误的是( ).①∠1和∠3是同位角；②∠1和∠5是同位角；③∠1和∠2是同旁内角；④∠1和∠4是内错角.A．①②B．②③C．②④D．③④【习题4】若∠1与∠2是同位角，则它们之间的关系是( ).A．∠1＝∠2；B．∠1＞∠2；C．∠1＜∠2；D．∠1＝∠2或∠1＞∠2或∠1＜∠2.【习题5】如图所示，直线a，b被直线c所截，∠1与∠2是（）A．同位角B．内错角C．同旁内角D．邻补角【习题6】已知图（1）—（4）：在上述四个图中，∠1与∠2是同位角的有（）.A．（1）（2）（3）（4）B．（1）（2）（3）C．（1）（3）D．（1）【习题7】如图，下列结论正确的是（）.A．∠5与∠2是对顶角；B．∠1与∠3是同位角；C．∠2与∠3是同旁内角；D．∠1与∠2是同旁内角.【习题8】在图中，∠1与∠2不是同旁内角的是（）.B C D【习题9】如图，当直线BC 、DC 被直线AB 所截时，∠1的同位角是_______，同旁内角是_______；当直线AB 、AC 被直线BC 所截时，∠1的同位角是________；当直线AB 、BC 被直线CD 所截时，∠2的内错角是________．【习题10】如图，(1)∠1和∠ABC 是直线AB 、CE 被直线________所截得的________角； (2)∠2和∠BAC 是直线CE 、AB 被直线________所截得的________角；(3)∠3和∠ABC 是直线________、________被直线________所截得的________角； (4)∠ABC 和∠ACD 是直线________、________被直线所截得的________角； (5)∠ABC 和∠BCE 是直线________、________被直线所截得的________角．【习题11】如图，若∠1＝95°，∠2＝60°，则∠3的同位角等于________，∠3的内错角等于________，∠3的同旁内角等于________．第9题第10题第11题A【习题12】如图，在图中的∠1、∠2、∠3、∠4、∠5和∠B中，同位角是________，内错角是________，同旁内角是________．【习题13】如图，直线a、b、c分别与直线d、e相交，与∠1构成同位角的角共有________个，和∠l 构成内错角的角共有________个，与∠1构成同旁内角的角共有________个．【习题14】如图，三条直线两两相交，其中同旁内角共有对，同位角共有对，内错角共有对.第12题第13题第14题。

人教版数学3年级下册第1单元(位置与方向一)用八个方向描述简单的行走路线课件(共41张PPT)

小猴家
小鹿家
小松鼠家
终点小狗家
②小兔家向东小猴家向西南小松鼠家向东南小狗家
小兔家起点
北
小猴家
小鹿家
小松鼠家
终点小狗家
③ 小兔家向东小猴家向西南小松鼠家向西南小鹿家向东小狗家
小兔家起点
北
小猴家
小鹿家
小松鼠家
终点小狗家
先到小猴家有3种不同的走法，先到小鹿家和小松鼠家都各有3种不同的走法。
小兔子住在森林的西南角，小鹿住在森林的东北角。
5. 西北
北东北
小松鼠住在森林的起点西北角，我先……
西南
终点
（2）小熊的送货路线是
西北
东
起点
东南
南
西
提升练习
1.从小兔家到小狗家有多少种不同的走法？
北
小兔家起点
小猴家
小鹿家
小松鼠家
终点小狗家
① 小兔家向东小猴家向南小狗家
小兔家起点
北
终点
（2）小亮家在学校的（东南）方向，他放学回家先向（南）走到超市，再向（东）走到家。
小林家
邮局
小明家北
学校
书店
小红家超市小亮家
（3）张老师从学校出发去四位同学家家访，路线是：
西南学校小红家
东
小亮家
北
小明家
西
东南小林家学校
起点
终点
3.如图是1路公交车的行车路线图。
北
火
车站
1 位置与方向（一）
第4课时用八个方向描述简单的行走路线
人教版数学三年级（下）
学习目标
1.能够用给定的一个方向，辨认其余的七个方向，会看简单的路线图（八个方向），并描述行走路线。

2016春季班提高班第1讲讲义

6
2016 年 -春季-五年级级-A 版
B
A
【解解析】最短路路径显然是 7+ +2+3=12 厘米米 (2)如如图是一个长长方体木块，长、宽、高分分别为 9 厘米米、7 厘米、5 厘米，一只只蜘蛛在 A 点，点蜘蛛蛛需要爬到点点 B 处，如果果只能沿着长长方体木块表面爬，最短路路径是多长？？
下面面的图形是以以直角三角形形 ABC 的三边边为直径向外外作半圆得到到，形成两个个月牙形图案案（阴影部部分），已知 AC A =10，BC C=6，求阴影影部分面积。
C
A
B
பைடு நூலகம்
【解解析】以 BC、AC、AB 为直径的半圆为圆面积分别记记为 S1 、 S2 、 S 3 ，整体面面积记为 S，那么阴影部部分面积 S阴影 =S S3 S ( S1 S 2 ) S ABC 10 6 2 30 .
A B D C
教学提示】此此例题主要涉涉及一些常见见辅助线，目的都是构造直角三角形以以利用勾股定定理. 【教拓展展题涉及到勾勾股逆定理，视情况补充 . 一练：练一两根根旗杆竖直插插在地面上，高度分别是 12 米、18 米，底端距离米离 8 米，两根根旗杆的顶部相距多少少米？
2016 年 -春季-五年级级-A 版
3
+
D
A
E
B
C
【解解析】如图连连接 AD，过点点 A 作 CD 垂线，垂足足为 E，由于 DE=CD-EC C=CD-AB=6 米， AE=BC C=8 米，所以以 AD=10 米，，顶部相距 10 米.

初中数学-春季班-人教版-初一(教师版) 第1讲相交线--尖子班

第1讲相交线知识点1 直线交点个数1. 两条直线交于一点，我们称这两条直线相交，相对的，我们称这两条直线为相交线．【典例】例1 （2020秋•邢台期中）观察如图，并阅读图形下面的相关文字：两条直线相交，最多有1个交点；三条直线相交，最多有3个交点；4条直线相交，最多有6个交点⋯⋯像这样，20条直线相交，交点最多的个数是()A．100个B．135个C．190个D．200个【解答】解：2条直线相交最多有1个交点，11122=⨯⨯，3条直线相交最多有3个交点，1312232=+=⨯⨯，4条直线相交最多有6个交点，1 6123342=++=⨯⨯，5条直线相交最多有10个交点，1 101234452=+++=⨯⨯，⋯n 条直线相交最多有交点的个数是：1(1)2n n -．20条直线相交最多有交点的个数是：11(1)201919022n n -=⨯⨯=．故选：C ．【方法总结】此题主要考查了相交线探索规律．此题在相交线的基础上，着重培养学生的观察、实验和猜想、归纳能力，掌握从特殊向一般猜想的方法是解题的关键．根据题意，结合图形，发现：3条直线相交最多有3个交点，4条直线相交最多有6个交点，5条直线相交最多有10个交点，故可猜想，n 条直线相交，最多有1123(1)(1)2n n n +++⋯+-=-个交点，据此解答即可.【随堂练习】1．（2020秋•鼓楼区校级月考）观察图形，下列说法正确的个数是( ) ①直线BA 和直线AB 是同一条直线； ②射线AC 和射线AD 是同一条射线； ③线段AC 和线段CA 是同一条线段； ④三条直线两两相交时，一定有三个交点．A ．1B ．2C ．3D ．4【解答】解：①直线没有方向，直线BA 和直线AB 是同一条直线，故①说法正确； ②射线AC 和射线AD 是同一条射线，故②说法正确； ③线段AC 和线段CA 是同一条线段，故③说法正确；④三条直线两两相交时，一定有三个交点，还可能有一个，故④说法不正确．共3个说法正确．故选：C ．2．（2019秋•旌阳区校级月考）在同一平面内的n 条直线两两相交，最多共有36个交点，则(n = ) A ．7B ．8C ．9D ．10【解答】解：2条直线相交最多有1个交点；3条直线相交最多有12+个交点；4条直线相交最多有123++个交点；5条直线相交最多有1234+++个交点；6条直线相交最多有12345++++个交点；⋯所以n条直线相交最多有(1)12345(1)2n nn-+++++⋯+-=个交点；由题意得(1)362n n-=，解得9n=．故选：C．知识点2 邻补角与对顶角邻补角1. 邻补角：两个角有一条公共边，他们的另一边互为反向延长线，具有这种关系的两个角互为邻补角.2. 邻补角的模型：∠1和∠3是邻补角，∠1和∠4是邻补角，∠2和∠3是邻补角，∠2和∠4是邻补角，特点：①成对出现；②两个角有公共的顶点；③两个角有一条公共边，另一边互为反向延长线.3. 邻补角的性质：两个角的和为180°.对顶角1. 对顶角的模型：∠1和∠2是对顶角，∠3和∠4是对顶角.特点：①成对出现；②两个角有公共的顶点；③每个角的两边互为另一个角的反向延长线. 2. 对顶角的性质：对顶角相等.【典例】例1 （2020春•哈尔滨月考）如图，已知直线AB 和CD 相交于点(45)O BOD ∠<︒．（1）写出AOD ∠与BOC ∠的大小关系：___________，依据是___________；（2）在BOC ∠的内部，过点O 作120COE ∠=︒，OF 平分AOE ∠，OG 平分AOC ∠，画出符合条件的图形，并求出EOF COG ∠-∠的度数；（3）在（2）的条件下，若OB 平分EOD ∠，求COF ∠的度数．【解答】解：（1）根据对顶角相等可得， AOD BOC ∠=∠，理由：对顶角相等，故答案为：AOD BOC ∠=∠，对顶角相等；（2）如图，OF 平分AOE ∠，12EOF AOF AOE ∴∠=∠=∠，又OG 平分AOC ∠，12COG AOG AOC ∴∠=∠=∠，11111()1206022222EOF COG AOE AOC AOE AOC COE ∴∠-∠=∠-∠=∠-∠=∠=⨯︒=︒；（3）120COE ∠=︒， 18012060DOE ∴∠=︒-︒=︒，又OB 平分DOE ∠，1302DOB BOE DOE ∴∠=∠=∠=︒，30AOC BOD ∴∠=∠=︒， 120COE ∠=︒，150AOE AOC COE ∴∠=∠+∠=︒，又OF 平分AOE ∠，1752AOF EOF AOE ∴∠=∠=∠=︒753045COF AOF AOC ∴∠=∠-∠=︒-︒=︒．【方法总结】本题考查对顶角、邻补角、角平分线的意义，掌握对顶角、邻补角、角平分线的定义是解决问题的前提，根据图形直观得出各个角之间的和差关系是正确解答的关键．例2 （2020春•雨花区校级月考）如图，直线AB ，CD 相交于点O ，OA 平分EOC ∠．（1）AOC ∠的对顶角为________，AOC ∠的邻补角为；（2）若70EOC ∠=︒，求BOD ∠的度数；（3）若:2:3EOC EOD ∠∠=，求BOD ∠的度数．【解答】解：（1）根据对顶角、邻补角的意义得，AOC ∠的对顶角为BOD ∠，AOC ∠的邻补角为BOC ∠或AOD ∠，故答案为：BOD ∠，BOC ∠或AOD ∠；（2）OA 平分EOC ∠．70EOC ∠=︒，1352AOE AOC EOC ∴∠=∠=∠=︒，又AOC BOD ∠=∠， 35BOD ∴∠=︒，（3）:2:3EOC EOD ∠∠=，180EOC EOD ∠+∠=︒， 72EOC ∴∠=︒，108EOD ∠=︒， OA 平分EOC ∠．1362AOE AOC EOC ∴∠=∠=∠=︒，又AOC BOD ∠=∠， 36BOD ∴∠=︒．【方法总结】本题考查对顶角、邻补角、角平分线、平角的意义和性质，通过图形具体理解这些角的意义是正确计算的前提．【随堂练习】1．（2020春•公主岭市期中）如图，直线AB ，CD 相交于点O ，OM AB ⊥．（1）AOC ∠的邻补角为________（写出一个即可）；（2）若12∠=∠，判断ON 与CD 的位置关系，并说明理由；（3）若114BOC ∠=∠，求MOD ∠的度数．【解答】解：（1）AOC ∠的邻补角为AOD ∠（或)COB ∠ 故答案为：AOD ∠；（2）结论：ON CD ⊥，证明：OM AB ⊥， 190AOC ∴∠+∠=︒，又12∠=∠，290NOC AOC ∴∠=∠+∠=︒， ON CD ∴⊥；（3）114BOC ∠=∠，41BOC ∴∠=∠，190BOC MOB ∠-∠=∠=︒， 130∴∠=︒，1801150MOD ∴∠=︒-∠=︒．2．（2020春•芝罘区期末）如图，已知直线AB ，CD 相交于点O ，90BOE ∠=︒．（1）若40BOD ∠=︒，求COE ∠的度数；（2）若:3:7AOC BOC ∠∠=，求DOE ∠的度数．【解答】解：（1）90BOE ∠=︒，40BOD ∠=︒， 90AOE ∴∠=︒，40AOC BOD ∠=∠=︒，则904050COE ∠=︒-︒=︒；（2）:3:7AOC BOC ∠∠=，∴设3AOC x ∠=，则7BOC x ∠=，180AOC BOC ∠+∠=︒， 37180x x ∴+=︒，解得：18x =︒， 54AOC ∴∠=︒， BOD AOC ∠=∠， 54BOD ∴∠=︒，9054144DOE BOE BOD ∴∠=∠+∠=︒+︒=︒．3．（2020春•五莲县期末）如图，直线AB ，CD 相交于点O ，OA 平分EOC ∠．（1）BOD ∠的补角是 AOD ∠和BOC ∠和BOE ∠ ；（2）若:2:3EOC EOD ∠∠=，求BOD ∠的度数．【解答】解：（1）BOD ∠的补角是AOD ∠和BOC ∠和BOE ∠，故答案为：AOD ∠和BOC ∠和BOE ∠；（2）设2EOC x ∠=，3EOD x ∠=，根据题意得：23180o x x +=，解得36o x =， 272o EOC x ∴∠==，11723622o o AOC EOC ∴∠=∠=⨯=，36BOD AOC ∴∠=∠=︒．知识点3 垂线垂线1. 两直线相交所形成的角中，当有一个角等于90°时，这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，他们的交点叫做垂足.2. 垂直的模型：说法：①直线a是直线b的垂线（或直线b是直线a的垂线），垂足为O.②直线a垂直于直线b于点O（或直线b垂直于直线a于点O）.结论：两垂直直线形成的四个角都是直角，均为90°.3. 在同一平面内，过一点有且只有一条直线与已知直线垂直.垂线段1. 过直线外一点作直线的垂线，以这个点和垂足为端点的线段叫做这个点到直线的垂线段.2. 垂线段模型：线段AB是点A到直线a的垂线段.3. 连接直线外一点与直线上各点的所有线段中，垂线段最短.简单说成：垂线段最短.4. 直线外一点到这条直线的垂线段的长度，叫做点到直线的距离.注意：距离是长度，不是线段.【典例】例1 （2020春•兴国县期末）如图，已知直线AB、CD、EF相交于点O，OG CD⊥，∠=︒．BOD24（1）求AOG∠的度数；（2）若OC是AOE∠的平分线吗？说明你的理由．∠的平分线，那么OG是AOF【解答】解：（1）AB 、CD 相交于点O ，24AOC BOD ∴∠=∠=︒， OG CD ⊥， 90COG ∴∠=︒，即90AOC AOG ∠+∠=︒，90902466AOG AOC ∴∠=︒-∠=︒-︒=︒；（2）OG 是AOF ∠的角平分线，理由如下：OC 是AOE ∠的角平分线， AOC COE ∴∠=∠，又DOF COE ∠=∠， COA DOF ∴∠=∠， OG CD ⊥，90COG DOG ∴∠=∠=︒， AOG GOF ∴∠=∠， OG ∴平分AOF ∠．【方法总结】本题考查了垂线，对顶角的定义，角平分线的性质等知识，灵活运用这些性质解决问题是本题的关键．例2 （2020春•钦州期末）如图，直线AB ，CD 相交于点O ，过点O 作OE AB ⊥，且OF 平分AOD ∠，已知24BOD ∠=︒．（1）求证：COF BOF ∠=∠；（2）求EOF ∠的度数．【解答】证明：（1）OF 平分AOD ∠， AOF DOF ∴∠=∠，又AOC BOD ∠=∠，AOF AOC DOF BOD ∴∠+∠=∠+∠，即COF BOF ∠=∠；（2）180********AOD BOD ∠=︒-∠=︒-︒=︒， 156278AOF DOF ∴∠=∠=︒÷=︒，又OE AB ⊥， 90BOE ∴∠=︒，902466EOD BOE BOD ∴∠=∠-∠=︒-︒=︒， 786612EOF DOF EOD ∴∠=∠-∠=︒-︒=︒．【方法总结】本题主要考查垂直的定义，平角的定义，角平分线的定义，对顶角的性质，灵活运用垂线的定义是解题的关键．例3 （2019秋•侯马市期末）如图，点P ，点Q 分别代表两个村庄，直线l 代表两个村庄中间的一条公路．根据居民出行的需要，计划在公路l 上的某处设置一个公交站．（1）若考虑到村庄P 居住的老年人较多，计划建一个离村庄P 最近的车站，请在公路l 上画出车站的位置（用点M 表示），依据是________________________________________；（2）若考虑到修路的费用问题，希望车站的位置到村庄P 和村庄Q 的距离之和最小，请在公路l 上画出车站的位置（用点N 表示），依据是_______________________________．【解答】解：（1）如图，点M即为所示．依据是直线外一点与直线上各点连接的所有线段中垂线段最短（2）如图，点N即为所示．依据是两点之间线段最短；故答案为：直线外一点与直线上各点连接的所有线段中垂线段最短；两点之间线段最短．【方法总结】此题主要考查了应用设计与作图，正确理解线段的性质是解题关键．【随堂练习】1．（2020春•黄埔区期末）如图，直线AB，CD相交于点O，EO AB⊥，垂足为O，∠=︒，则EOC∠的度数为_________．AOD118【解答】解：118AOD∠=︒，∴∠=∠=︒，118BOC AOD⊥，EO AB∴∠=︒，BOE90∴∠=∠-∠=︒，28EOC BOC BOE故答案为：28︒．2．（2020春•大新县期末）如图，直线AB与CD相交于点O，OP是BOC∠的平分线，⊥于点O，FO CD⊥于点O．EO AB（1）若40∠的度数；AOD∠=︒，求EOC（2）若:1:5AOD EOF ∠∠=，求BOP ∠的度数．【解答】解：（1）EO AB ⊥， 90AOE ∴∠=︒． 40AOD ∠=︒，180EOC AOD AOE ∴∠=︒-∠-∠ 1804090=︒-︒-︒50=︒．（2）:1:5AOD EOF ∠∠=，设AOD ∠为x ︒，则EOF ∠为5x ︒ DO FO ⊥， 90DOF ∴∠=︒．360AOD AOE EOF DOF ∠+∠+∠+∠=︒， 90590360x x ∴+︒++︒=︒．解得30x =︒，即30AOD ∠=︒．又30BOC AOD ∴∠=∠=︒（对顶角相等）， OP 是BOC ∠的平分线，11301522POB BOC ∴∠=∠=⨯︒=︒．3．（2020春•长安区校级月考）下列说法： ①两点之间的所有连线中，线段最短；②在同一平面内，过一点有且只有一条直线与已知直线垂直； ③连接直线外一点与直线上各点的所有线段中，垂线段最短；④直线外一点到这条直线的垂线段叫做点到直线的距离，其中正确的个数有( ) A ．4个B ．3个C ．2个D ．1个【解答】解：①两点之间的所有连线中，线段最短，说法正确；②在同一平面内，过一点有且只有一条直线与已知直线垂直，说法正确；③连接直线外一点与直线上各点的所有线段中，垂线段最短，说法正确；④直线外一点到这条直线的垂线段的长度叫做点到直线的距离，说法错误．故选：B．知识点4 同位角、内错角、同旁内角模型：1. 同位角：两条直线被第三条直线所截形成的角中，若两个角分别在两直线的同一方，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．如∠1与∠8，∠2与∠5.2. 内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线之间，并且在第三条直线（截线）的两侧，则这样一对角叫做内错角．如∠1与∠6，∠4与∠5.3. 同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线之间，并且在第三条直线（截线）的同一旁，则这样一对角叫做同旁内角．如∠1与∠5，∠4与∠6.4. 三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U” 形.【典例】例1（2020秋•杨浦区校级期中）如图，共有_____对同位角，有对内错角，有对同旁内角．【解答】解：同位角：AEO ∠和CGE ∠，OEF ∠和EGH ∠，OFB ∠和OHD ∠，OFE ∠和OHG ∠，IGH ∠和IEF ∠，AEI ∠和CGI ∠，AFJ ∠和CHJ ∠，DHJ ∠和JFB ∠，AEO ∠和AFO ∠，OEB ∠和OFB ∠，AEG ∠和AFH ∠，GEB ∠和HFB ∠，EGH ∠和OHD ∠，OGC∠和OHC ∠，O ∠与EFH ∠，O ∠与GEF ∠，O ∠和IGH ∠，O ∠和GHJ ∠， CGI ∠和CHJ ∠，HGI ∠和DHJ ∠，共20对；内错角：O ∠和OEA ∠，O ∠和OFB ∠，O ∠和OGC ∠，O ∠和OHD ∠，AEG ∠和EGH ∠，BEG ∠和EGC ∠，BFH ∠和FHC ∠，AFH ∠和FHD ∠，OEF ∠和EFH ∠，GEF ∠和OFE ∠，OGH ∠和GHJ ∠，OHG ∠和IGH ∠，共12对；同旁内角：OEF ∠和O ∠，OFE ∠和O ∠，O ∠和OGH ∠，O ∠和OHC ∠，OEF ∠和OFE ∠，OGH ∠和OHG ∠，GEF ∠和EFH ∠，IGH ∠和GHJ ∠，AEG ∠和CGE ∠，BFH ∠和FHD ∠，FEG ∠和EGH ∠，EFH ∠和GHF ∠，共12对，故答案为：20；12；12．【方法总结】此题主要考查了同位角、内错角、同旁内角，关键是掌握同位角的边构成“F “形，内错角的边构成“Z “形，同旁内角的边构成“U ”形．例2（2020春•自贡月考）如图，1∠的同位角是_______；1∠的内错角是； 1∠的同旁内角是．【解答】解：1∠的同位角是EFG ∠；1∠的内错角是DCB ∠，DEA ∠；1∠的同旁内角是DFG ∠、DEC ∠、DCA ∠．故答案为：EFG ∠；DCB ∠，DEA ∠；DFG ∠、DEC ∠、DCA ∠．【方法总结】此题主要考查了同位角、内错角、同旁内角，关键是掌握同位角的边构成“F “形，内错角的边构成“Z “形，同旁内角的边构成“U ”形．【随堂练习】1．（2020春•西湖区期末）如图，有下列3个结论：①能与DEF ∠构成内错角的角的个数是2；②能与EFB ∠构成同位角的角的个数是1；③能与C ∠构成同旁内角的角的个数是4，以上结论正确的是_______．【解答】解：①能与DEF ∠构成内错角的角的个数有2个，即EFA ∠和EDC ∠，故正确； ②能与EFB ∠构成同位角的角的个数只有1个：即FAE ∠，故正确；③能与C ∠构成同旁内角的角的个数有5个：即CDE ∠，B ∠，CED ∠，CEF ∠，A ∠，故错误；所以结论正确的是①②．故答案为：①②．2．（2020春•江城区期末）两条直线被第三条直线所截，1∠和2∠是同旁内角，3∠和2∠是内错角．（1）根据上述条件，画出符合题意的示意图；（2）若132∠=∠、233∠=∠，求1∠，2∠的度数．【解答】解：（1）如图所示：（2）132∠=∠、233∠=∠，193∴∠=∠， 13180∠+∠=︒， 933180∴∠+∠=︒， 318∴∠=︒，1162∴∠=︒，254∠=︒．综合运用1．（2020春•哈尔滨月考）如图，AB 、CD 交于点O ，OE 平分AOB ∠，若:5:4AOC COE ∠∠=，则AOD ∠等于( )A ．120︒B ．130︒C ．140︒D ．150︒【解答】解：OE 平分AOB ∠， 90AOE ∴∠=︒， 90AOC EOC ∴∠+∠=︒， :5:4AOC COE ∠∠=， 590509AOC ∴∠=︒⨯=︒，18050130AOD ∴∠=︒-︒=︒．故选：B ．2．（2020秋•朝阳区校级期中）如图，AB 与CD 相交于点，则下列结论一定正确的是()A ．13∠>∠B ．245∠<∠+∠C ．34∠=∠D ．35∠=∠【解答】解：A ．12∠=∠，13A ∠=∠+∠， 13∴∠>∠，故本选项符合题意；B ．245∠=∠+∠， 24∴∠>∠，25∠>∠，故本选项不合题意； C ．AD 与BC 不平行，34∴∠≠∠，故本选项不合题意；D ．A C ∠≠∠，35∴∠≠∠，故本选项不合题意；故选：A ．3．（2020•昆明模拟）如图所示，下列说法中错误的是( )A ．A ∠和3∠是同位角B ．2∠和3∠是同旁内角C ．A ∠和B ∠是同旁内角D ．C ∠和1∠是内错角【解答】解：A 、A ∠和3∠是同位角，此选项说法正确；B 、2∠和3∠是邻补角，此选项说法错误；C 、A ∠和B ∠是同旁内角，此选项说法正确；D 、C ∠和1∠是内错角，此选项说法正确；故选：B ．4．（2020春•新泰市期末）如图，在铁路旁有一李庄，现要建一火车站，为了使李庄人乘车最方便，请你在铁路线上选一点来建火车站，应建在( )A ．A 点B ．B 点C ．C 点D ．D 点【解答】解：根据垂线段最短可得：应建在A 处，故选：A ．5．（2019春•和平区期末）下列说法中正确的是( ) A ．有且只有一条直线垂直于已知直线B ．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离C ．互相垂直的两条线段一定相交D ．直线c 外一点A 与直线c 上各点连接而成的所有线段中最短线段的长是3cm ，则点A 到直线c 的距离是3cm【解答】解：A 、和一条直线垂直的直线有无数条，故A 错误；B 、直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，不是指点到直线的垂线段的本身，而是指垂线段的长度，故B 错误；C 、互相垂直的两条线段不一定相交，线段有长度限制，故C 错误；D 、直线c 外一点A 与直线c 上各点连接而成的所有线段中最短线段就是垂线段，可表示点A 到直线c 的距离，故D 正确．故选：D ．6．（2019秋•卫辉市期末）如图，AOC ∠为平角，已知OE 平分AOB ∠，OF 平分BOC ∠，AC 与DF 相交于点O ，25AOD ∠=︒，则BOE ∠的度数为 65︒ ．【解答】解：OE 平分AOB ∠，OF 平分BOC ∠， 12AOE EOB AOB ∴∠=∠=∠，12COF BOF BOC ∠=∠=∠，AOC ∠为平角，180AOB BOC ∴∠+∠=︒ 90EOB BOF EOF ∴∠+∠=∠=︒25AOD COF ∠=︒=∠， 902565BOE ∴∠=︒-︒=︒，故答案为：65︒．7．（2020秋•虎林市期末）如图，点O 在直线AB 上，OD OE ⊥，垂足为O ，OC 是DOB ∠的平分线，若70AOD ∠=︒，则BOE ∠=______度，COE ∠= 度．【解答】解：180110BOD AOD ∠=︒-∠=︒，又OC 是DOB ∠的平分线． 1552DOC COB BOD ∴∠=∠=∠=︒，OD OE ⊥，垂足为O ．90905535COE DOC ∴∠=︒-∠=︒-︒=︒， 553520BOE COB COE ∠=∠-∠=︒-︒=︒．故答案是：20和35．8．（2019春•红塔区期中）如图，直线AB 、CD 相交于点O ，OE 把BOD ∠分成两部分；（1）直接写出图中AOC ∠的对顶角为 BOD ∠ ，BOE ∠的邻补角为；（2）若70AOC ∠=︒，且:2:3BOE EOD ∠∠=，求AOE ∠的度数．【解答】解：（1）AOC ∠的对顶角为BOD ∠，BOE ∠的邻补角为AOE ∠；故答案为：BOD ∠，AOE ∠；（2）70DOB AOC ∠=∠=︒，DOB BOE EOD ∠=∠+∠，:2:3BOE EOD ∠∠=，∴32EOD BOE ∠=∠，∴3702BOE BOE∠+∠=︒，28BOE∴∠=︒，180152AOE BOE∴∠=︒-∠=︒．21。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三年级春季第 8 讲点线排布（B 版）
3
个交点；（3）若平面上有 n 条直线，则每增加一条直线，交点数最多增加 n-1 个，所以 101 条直线最多有 1 2 3 每条线上有 100 个交点．同一平面上的 8 条直线最多可以有几个交点？【答案】28 【分析】 7 6 5 4 3 2 1 28 （1）把 6 棵树排成 3 行，保证每行有 3 棵树，应该如何排？（2）在（1）的基础上，你能不能只移动其中一棵树，变成 4 行，每行 3 棵呢？（3）把 7 棵树排成 5 行，保证每行有 3 棵树，应该如何排？【答案】（1）如图：
【答案】如图（不唯一）：
5个交点
6个交点
7个交点
8个交点
（1）在同一平面上任给 3 个点，可以确定几条直线？试着画一画．
2
三年级春季第 8 讲点线排布（B 版）
（2）在同一平面上任给 4 个点，可以确定几条直线？试着画一画．（3）在同一平面上任给 10 个点，最多可以确定几条直线？【答案】（1）1 或 3；（2）1，4 或 6；（3）45 【分析】（1）三点共线时 1 条，不共线 3 条；（2）四点共线 1 条；三点共线 4 条，无三点共线 6 条；（3）要想确定的直线最多，应不存在三点共线的情况，所以任意两个点都能确定一条不同的直线．从第一个点出发，可确定 9 条直线；再从第二个点出发，可以确定 8 条直线，以此类推（类似数线段），所以最多可以确定
三年级春季第 8 讲点线排布（B 版）
5
8
点线排布
预习
下图中有几条直线？几个交点？能否在图中添加一条直线，使图中分别有 7、8 、9 、11 个交点？
【答案】5 条直线，6 个交点【分析】如图（不唯一）：
7个交点点
11个交点
在下图中加入一条直线，使得图中分别有 5、6、7、8、 9 个交点．
【答案】如图：
三年级春季第 8 讲点线排布（B 版）
987
2 1 45 条直线．
（1）同一平面上的 3 条直线最多可以有几个交点？每条线上有几个交点？（2）同一平面上的 4 条直线最多可以有几个交点？每条线上有几个交点？（3）同一平面上的 101 条直线最多可以有几个交点？每条线上有几个交点？【答案】（1）3；2；（2）6；3；（3）5050；100 【分析】（1）3 条直线最多有 1 2 3 个交点，每条线上有 2 个交点；（2）4 条直线最多有 1 2 3 6 个交点，每条线上有 3
1
5个交点
6个交点
7个交点
8个交点
9个交点
【分析】本题推荐练习 8 个点的情况，要增加 4 个点，需要与 4 条直线相交，对于两组平行线来说，只要与其中一条相交，那么一定会与另外一条相交，因此新加的这条线只能与斜线平行．图中共 6 条直线 9 个交点，去掉 1 条直线，使交点个数分别为 5、6、7、8 个．
99 100 5050 个交点，
（2）如图：
4
三年级春季第 8 讲点线排布（B 版）
（3）可以在 6 树 3 行的基础上增加一个点，如图：
如图，把 8 棵树排为 4 行，保证每行有 3 棵，你能不能移动 1 棵树，变为 5 行每行有 3 棵？
【答案】如图：
把 10 棵树排为 5 行，保证每行有 4 棵，应该如何排？【答案】如图：